解算某二次超静定梁弯矩内力方法探究

杨 青 杨国兵

(1.滁州学院土木与建筑工程学院，安徽 滁州 239000； 2.安徽滁州技师学院，安徽 滁州 239000)

0 引言

自各种结构设计软件开发、运用、改版、升级以来，结构设计人员的精力得以释放，伴随我国基本建设新建、扩建、改建、加固项目的规模化、复杂化、新颖化、个性化，无论是大跨、多高层建筑、市政桥梁工程，还是公路、铁路隧道及矿山井筒等工程结构物的设计，结构设计软件(如SAP系列，MIDAS，STAAD PRO，ANSYS，PKPM等)均大显身手，但作为结构设计人员对力学结构的框架概念及软件建模计算参数的拾取，特别是对计算机软件程序计算结果的正确性的甄别，具备基本的运算能力绝不容忽视。即针对结构或构件所受的荷载效应(或作用效应)，绘制内力图的能力，再进行结构抗力的设计，如解决不太复杂的梁、刚架、桁架、拱、组合结构(特别是超静定结构)构件在荷载、温度、支座位移等因素影响下的内力图等问题。超静定结构在工程实体的应用十分广泛，超静定结构内力的解算历来是结构力学解算的重难点，因此，为解决工程实践问题或直接服务于工程实际的超静定梁的内力的不同解算方法值得研究。

1 算例的提出

结构设计人员可以有多种方法求解超静定题，到底哪种方法更便捷、高效。不妨采用探究法以察题效：如图1所示的二次超静定梁，用力法、位移法和弯矩分配法分别求解其弯矩图(EI为常数)。

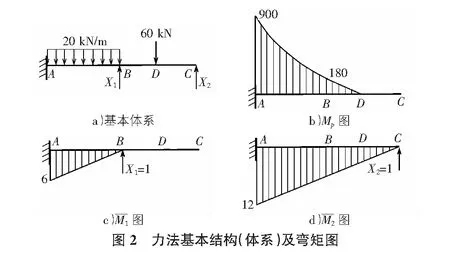
2 三种方法求解算例

2.1 力法

本算例先按常规方法去除多余未知量，选取图2a)为基本体系，建立力法典型方程如下。图乘法过程如图3所示。

(1)

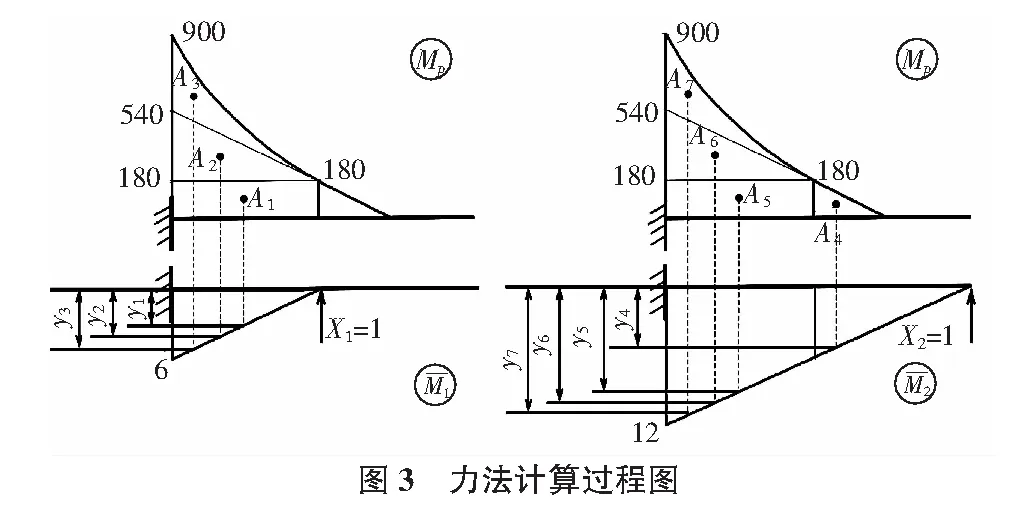
2.2 位移法求解

采用“附加刚臂”原理，“先紧后松”，利用“形常数”与“载常数”[1]。求解过程见图5。

2.3 弯矩分配法求解

1)计算线刚度：

2)各杆的抗转刚度及分配系数：

SBA=4×1=4,SBC=3×1=3,

3)各杆的固端弯矩：

B的不平衡弯矩：

4)分配弯矩及传递弯矩：

5)计算杆端的最终弯矩：

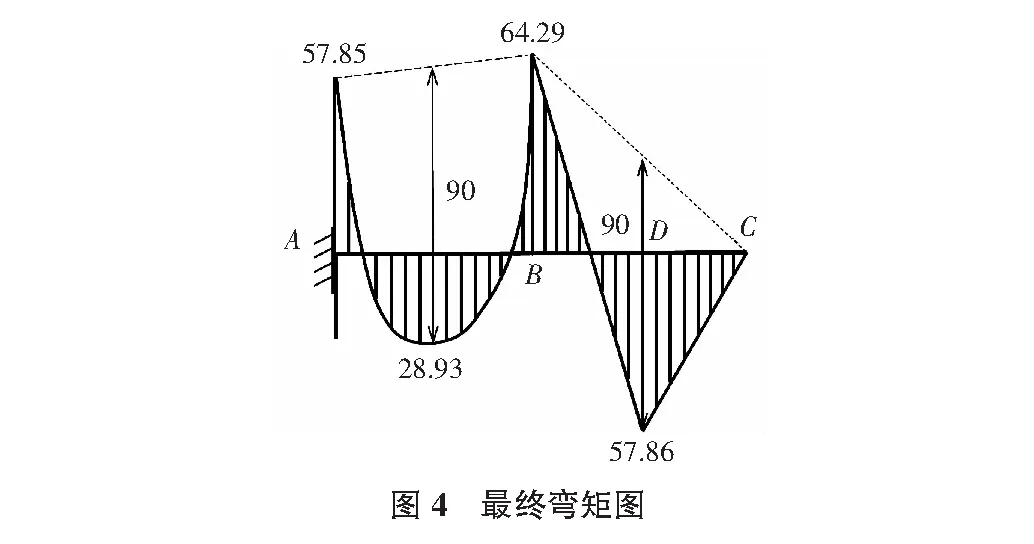
弯矩分配法的过程见表1。最终弯矩图同图4。

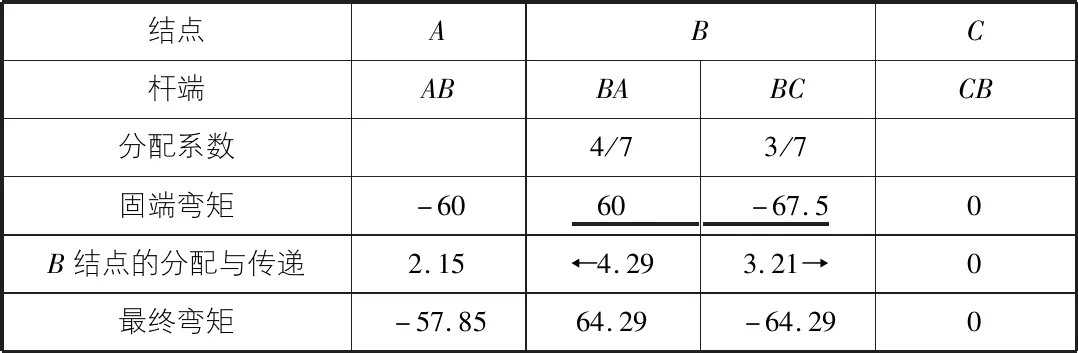
表1 杆端弯矩的计算

3 三种方法比较

在完成力法、位移法、弯矩分配法这三种方法的求解之后，将这三种方法的计算工作量进行对比，见表2。对比发现：弯矩分配法虽然需要将线刚度、抗转刚度、分配系数、固端弯矩、分配与传递弯矩以及最终弯矩共六大概念参数一一求出，看似步骤较多，却因无需图乘，无需列方程，更无需解方程，只需直接套用单跨超静定梁形常数表和载常数表计算，计算过程环环有序，实则简单。而力法在运用图乘法时计算工程量大，远比弯矩分配法复杂得多。位移法由于只有一个角位移，只需列一个典型方程，利用节点平衡求出相关系数，可见位移法计算过程较简单。

表2 三种方法计算工作量对比

4 力法不同基本结构

力法作为求解超静定结构基本方法之一，大概缘于与静定结构位移计算内容衔接之故，但力法的具体过程取决于基本结构的选取不同而又富有技巧[2-4]。简洁高效的基本结构见图6(图乘见图7)，图8(图乘见图9)。

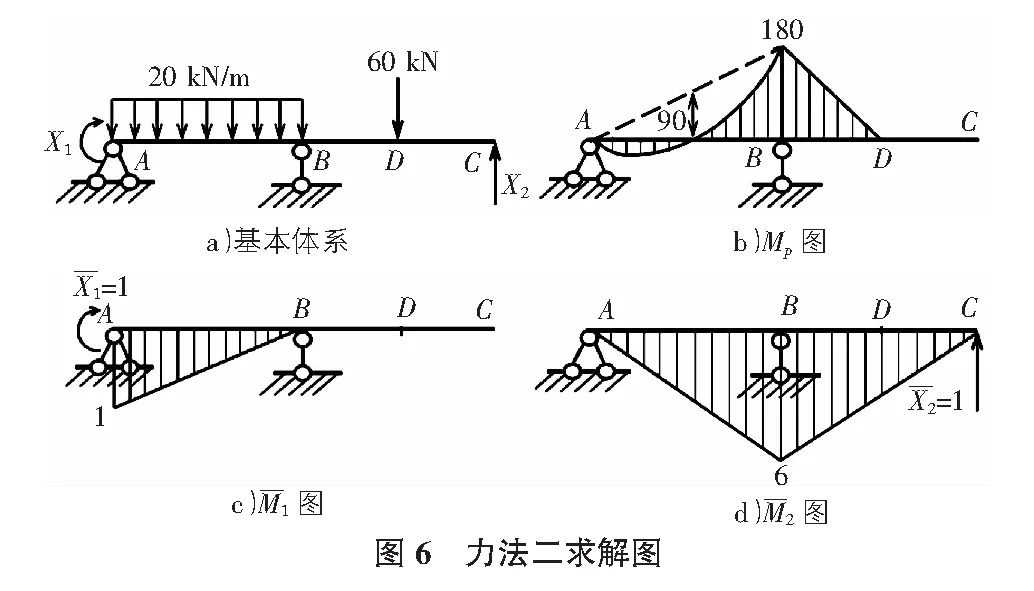
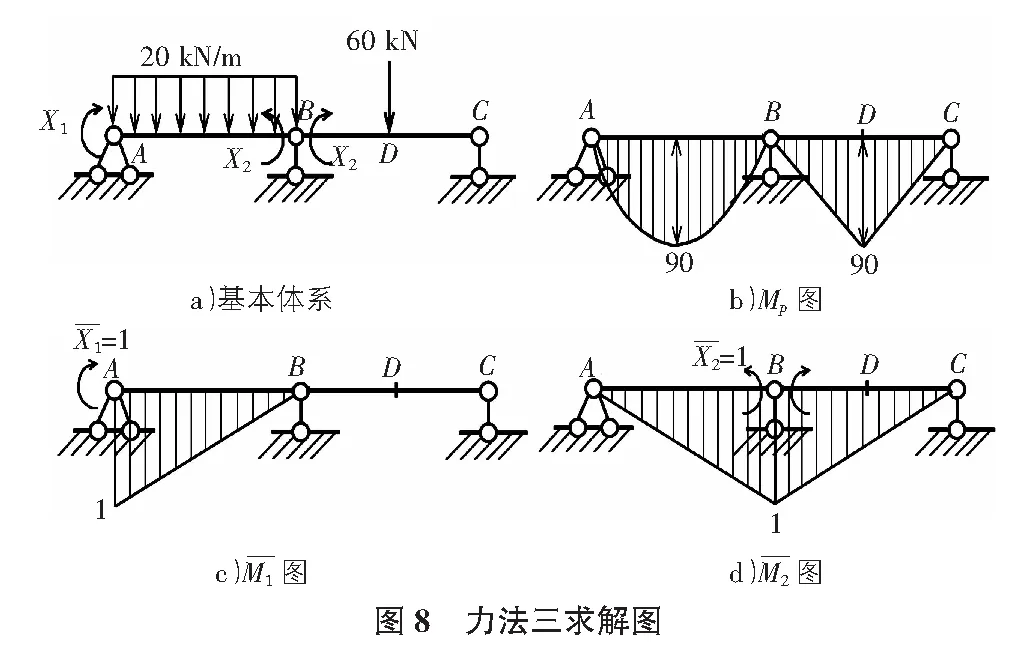
基本未知力为2个，力法典型方程仍为式(1)。

式中：

A3=270,y3=5,A4=18,y4=120,A5=360,y5=3,

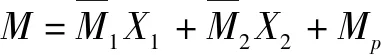
同理，力法三典型方程相关系数计算如下：

很明显，在第三种力法计算中，图乘过程变得简洁而顺畅，最后弯矩见图4。反思发现，用弯矩作为未知力代表多余约束，图乘时用到的面积是标准图形，计算难度降低，计算工作量大大减小(见表3)。

表3 三种力法自由项工作量对比

5 结语

1)通过对手算的二次超静定梁的三种不同的求解弯矩图对比，发现力法解题位移方程的系数，采用图乘法次数较多，较为繁琐，叠加分割的图形面积和形心位置容易出错，力法解题，基本结构的选取不同，解题的工作量有较大区别，当用弯矩作为未知力代表多余约束，图乘时用到的面积是标准图形，计算难度降低，计算工作量大大减小。

2)力矩分配法，概念较为清晰，易于操作，不易出错，深受工程技术青睐。但位移法前提是必须掌握单跨超静定梁的形常数与载常数图形的意义，达到灵活运用。

3)通过思考、解算、比较、总结等途径去主动探究问题的方法适合结构力学在工程结构计算中的应用，有助于提高结构设计人员考察分析判断结构构件软件计算结果的能力，值得推广。