基于IMU智能安全帽姿态估计

马明刚 严家常 郑贤喜 金超 黄彦庆

(1.国网新源浙江宁海抽水蓄能有限公司 浙江宁波 315000； 2.四川超影科技有限公司 成都 610065)

0 引言

安全帽是防止物体碰到头部的保护装置，在现代工程中是非常重要的安全保护措施之一。在电力、地质、林业和矿业等工作环境有危险的领域都有很广泛的应用。随着现代工程中的安全需求越来越高，新型智能安全帽应运而生。新型智能安全帽一般包括位置定位、安全感知、安全预警和远程通信等功能。而安全帽的姿态估计是安全预警的前提条件之一。

近年来，不少学者使用紧凑型MEMS-IMU(微机电系统-惯性测量单元)进行了关于姿态估计的广泛研究。MEMS-IMU主要由三轴陀螺仪(测量角速度)、三轴加速度计(测量外部加速度和重力之和)和三轴磁传感器(测量地球磁场)组成。这些传感器中的每一个都可以单独使用，以相对较低的精度推断出姿态[1]。因此，如何克服每个传感器单独使用时出现的缺点以及如何有针对性地结合惯性和磁传感器测量[2]，是设计姿态估计方法时要解决的关键问题。

物体姿态估计一般分为以下两种思路。第一种使用磁力计和加速度计，并包括确定性方法[3]，找到姿态矩阵即可。这些方法是通过运动是静态的或准静态的还原假设来设计的。在可以观察到显着的外部加速度的情况下，这种假设是无效的。在这种情况下，由于不能直接分离外部加速度和重力，因此难以高精度地检索姿态。第二种思路是结合陀螺仪、加速度计和磁力计，包括使用基于卡尔曼滤波器(KF)的非线性观测器的经典滤波方法[4]。一种使用线性观测模型的新型四元数卡尔曼滤波器(QKF)被提出，其测量噪声的协方差中添加了基于函数噪声的对角矩阵[5]。

本文智能安全帽姿态估计采用第二种思路。在实验平台智能安全帽中安装MEMS-IMU，通过其包含的三轴加速度计、三轴陀螺仪和三轴磁力计得到相关数据。物体的加速度数据和陀螺仪测得的在频域上能够实现特性互补[6]，根据磁力计传感器的数据反馈，可以提高系统的精度。将3个传感器的数据融合成四元数，再将四元数转换成欧拉角，得到智能安全帽的姿态信息。

1 智能安全帽的姿态

1.1 欧拉角描述姿态

欧拉角是一种常见的姿态描述方式，其可以体现出一个坐标系到另一个坐标系的变换方式，通过绕不同坐标轴的3次连续转动来实现[7]。欧拉角是这3次转动角度的统一称呼。为了更好地描述文中实验平台的方位及位置信息，定义了坐标系如图1所示。图中包括大地坐标系O-XYZ和安全帽坐标系P-UVW。大地坐标系是以地球为参考的。

研究使用航空次序欧拉角，定义其转动顺序为Z-Y-X，绕Z轴转动为偏航角(Yaw)，绕Y轴转动为俯仰角(Pitch)，绕X轴转动为横滚角(Roll)。

偏航角(Yaw)：智能安全帽坐标系X轴投影到水平面与参考系X轴的夹角，规定顺时针旋转为正。俯仰角(Pitch)：智能安全帽坐标系X轴与水平面的夹角，规定仰角为正。横滚角(Roll)：安全帽系Z轴与通过安全帽系X轴的铅垂面间的夹角，规定安全帽右旋为正。

图1 大地坐标系和智能安全帽坐标系相对位置

1.2 四元数描述物体姿态

旋转矩阵可以直观地表示出物体的姿态，但是旋转矩阵有9个分量，显得十分冗余。同样可以表征旋转的还有欧拉角，但是欧拉角具有万向节锁问题[8]，给计算解析造成很大麻烦。本研究选用在惯性导航中物体的空间姿态表示方法四元数，其一般由3个虚部和一个实部构成，一般形式为

Q=[qW,qX,qY,qZ]=qW+qXi+qYj+qZk(1)

Q=[Nsin(α/2)，cos(α/2)] (2)

四元数乘法和多项式相乘很类似，可以理解为再作一次上述定点转动变换，用Q'表示，即可以等效为一个转动四元数。

Q0=Q⊗Q'(3)

1.3 相关角度的测量

当智能安全帽处于静止状态时，加速度计只受到重力这一个作用力。当安全帽与水平面完全平行时，加速度计的理论输出值是[0,0,g](g是所在地区重力加速度大小)。当智能安全帽以一定角速度倾斜于水平面时，其各方向上输出值不一样，但其合成模值为1 G。

实际上，在智能安全帽处于静止状态且有倾斜角度时，如图2所示，加速度计此时所测量的数据是重力加速度在其坐标系下的投影。借助于三角函数关系，可以计算出智能安全帽的姿态角。

图2 物体姿态角和加速度之间的三角函数关系

2 四元数法姿态估计

通过四元数的分解进行物体的准静态姿态估计。该算法从四元数的物理意义出发，把载体的转动分解并合成以求得其姿态四元数。一般都是使用三参数法推导四元数，这会导致结果出现奇异值问题[9]。针对这个问题，提出使用转轴补偿的方法改正奇异值，可以实现智能安全帽的全姿态估计，同时提高其姿态估计的准确率。

2.1 分解四元数

假设智能安全帽与地球坐标系重合，设绕Z轴转动的，称为航向角(Yaw)，记为φ；绕Y轴转动的，称为俯仰角，记为θ；绕过X轴转动的，称为横滚角(Roll),记为γ。这样智能安全帽相对于地球坐标系的任意姿势都可以用对应的欧拉角表示出来，分别求出各个方向的欧拉角四元数，再合成姿态四元数即是智能安全帽的姿态描述。

2.1.1 航向角四元数

求航向角之前，先要转换到水平平面上，根据式(4)可以求得智能安全帽所在地等效的磁感性强度。令智能安全帽航向角为φ时，其所在地的磁感应强度mb=[mbX,mbY,mbZ]。这时，智能安全帽和地球磁场在水平方向的磁感应强度关系为

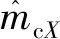
因φ∈(-π，π]，则得到航向角的旋转四元数为

(6)

2.1.2 俯仰角四元数

一般来说，物体水平方向的旋转不会影响其垂直方向的姿态。在智能安全帽静止时，测得的加速度a=[0,0,g]T,若智能安全帽绕Y轴旋转一定角度θ，则加速度在Y轴的分量仍为0，即为

aX=-gsinθ,aZ=gcosθ(7)

应用式(8)将加速度数据归一化为

根据归一化后的三角函数关系，有

式中，sign(a)为取符函数。

2.1.3 横滚角四元数

横滚角四元数X轴分量aX不变，aY,aZ为

aY=gcosθsinγ,aZ=gcosθcosγ

(12)

这时横滚角的正、余弦值分别为

横滚角γ∈(-π，π]，则横滚角的四元数为

在求出智能安全帽的俯仰角、横滚角和航向角的3个四元数之后，将这3个四元数分量进行合成后便可得到智能安全帽姿态四元数，合成公式为

qm=qφ⊗qθ⊗qγ(15)

在传统的静态姿态估计算法中，常常会由于磁感应模型的非精确匹配造成物体竖直方向姿态估计产生误差，文中上述方法能有效减小该误差。

3 补偿转轴方法

文中介绍的分解-合成四元数算法是利用智能安全帽固有的重力加速度g以及智能安全帽所在地的磁场强度作为参考的，可以在一定程度上消除磁感应模型非精确匹配造成的估计误差[10]。但是过程中在一定情况下会出现奇异值点问题，这里需要采取一定措施予以修正。

根据式(13)求俯仰角时，就有可能会出现分母为0的情况，此时通过分解四元数来进行智能安全帽姿态估计是无法进行的。针对这个问题，主流的解决方法是借角法[11]。其基本过程是在俯仰角θ无限接近于±π/2时，将俯仰角再转过一定角度φ，这时的等效俯仰角即为θ-φ。在分解四元数时，智能安全帽相应的原始加速度和其所在地磁感应强度数据也作相应四元数转化。这样得到相应的四元数后，再转化为实际的姿态四元数。

借角法能解决上述的奇异值问题，但是其不足之处在于会增加大量运算，加大时间损耗，不利于实现算法的实时性。文中提出补偿转轴方法来修正奇异值，以实现智能安全帽的实时全姿态估计。

首先将加速度数据和智能安全帽所在地的磁感应强度数据转轴匹配为智能安全帽在另一侧水平面的数据；然后将俯仰角设为0，根据前面公式计算横滚角和航向角所对应的四元数；接着把原本的俯仰角所对应的四元数代入式(15)，合成新的四元数。

当实验平台智能安全帽是由水平正面向上沿俯仰角方向转至竖立(左侧正面，右侧反面)时会出现奇异值问题。这时，应用上述的补偿转轴方法，即将处于竖直状态的智能安全帽惯性数据匹配至反面位置，可以推算出反面位置中X轴数据应该是竖立位置中Z轴测得数据的相反数，并且Z轴数据为竖立位置中X轴测得数据。这时将竖立位置的惯性数据转轴匹配，分解四元数即得到智能安全帽的奇异值点的姿态信息。

补偿转轴的本质是目标物体所在坐标系的转变。上述方法即是将智能安全帽从之前的Z-Y-X轴转换为Z-X-Y轴，这并不能从根本上消除奇异值点，而是将奇异值点转移至不影响运算的位置。

4 实验结果分析

通过智能安全帽实验平台(见图3)验证文中姿态估计方法可行性。智能安全帽中的MEMS-IMU系统架构如图4所示。智能安全帽姿态估计验证系统主要是由MEMS传感器、微处理器和上位机组成。软件部分采用Matlab2016b作为算法验证平台，以便于实现补偿转轴和分解四元数算法。

在实验过程中，由于四元数不能直观地反映出智能安全帽的姿态信息，因此在实验结果中将四元数转换为欧拉角显示出来，并且将航向角由-180°～180°的表示方式改为0°～360°来显示。

将智能安全帽放置水平在面上，沿其自身所在坐标系正向旋转，每次旋转一圈后都在某个点停留几秒，之后继续旋转，重复7次。部分实验结果可视化后如图5～图7所示。

图3 智能安全帽实验平台

图4 智能安全帽验证系统架构

图5 航向角变化可视化结果

图6 俯仰角变化可视化结果

图7 横滚角变化可视化结果

由于智能安全帽的主要应用场景是水平方向，分解四元数法将磁感应数用于水平方向上的航向角的姿态估计，但并不涉及到垂直方向上俯仰角和横滚角的姿态计算，在一定程度上可以减小磁感应模型的干扰所带来的误差。

5 结论

提出以MEMS-IMU为基础的智能安全帽姿态估计算法，根据智能安全帽的加速度和磁感应强度数据的四元数分解，以及和角速度的微分关系可以得到智能安全帽的姿态。同时，针对姿态估计过程中存在奇异值点的问题，提出补偿转轴的方法，可以实现智能安全帽的全姿态估计，这对于智能安全帽在工业安全预警中的应用很有帮助。实验结果显示，文中算法可以满足实时应用的要求。