地下构筑物挡水效应对地表沉降参数敏感性影响分析

王城斌， 于清杨， 刘 晨， 张 超， 刘 伟， 宋泽宇

(吉林大学建设工程学院，长春 130012)

地面沉降不仅危及人类位于地表及地下的已建工程构筑物，还会限制城市的进一步开发和建设。在全球面临气温升高导致海平面上升问题的当下，地面沉降对沿海城市和地区影响尤甚。导致地面沉降的人为影响因素众多，例如基坑、隧洞的开挖，地表高层、超高层建筑建设，地下水的开采等[1-7]，随着人类社会的日益发展，超大及特大城市不断涌现，城市地面沉降日益显著，特别是近几十年，全世界范围内已有多个城市的发展受到由于过量开采地下水所引起的地面沉降的困扰。蔡文晓认为，在德州市，由深层地下水的超量开采引起的地面沉降占总沉降量高达90%，且由地下水的开采引起的地面沉降影响范围较大[8]。

基于有效应力原理可知，抽水引起的地面沉降是由孔隙静水压力降低，土体有效应力增大所致[9]。对于抽水所引起的地面沉降，丁德民等认为，基于比奥固结理论建立的渗流场和应力场有限元耦合模型进行的地面沉降计算结果与实际情况吻合度良好[10]。

大量研究表明地下构筑物的存在会降低地下土体的渗透系数[11-14]。许烨霜分析地下挡水构筑物对土体渗透性的影响时采用等效介质理论计算等效渗透系数，进而分析计算挡水构筑物对地面沉降的影响，得到了挡水构筑物的设置会增大地面沉降量的结论[15]。但是，这种等效介质计算理论并未将地下构筑物位置的影响考虑在内，土体不同位置的水头变化也很难准确监测或分析计算得到，且用目前广泛采用的固结沉降理论和解析解方法计算抽水所引起的地面沉降往往没有考虑土层的侧摩阻力[16-17]，只能得到实际情况的近似解。为了分析地下构筑物对抽水引起的地面沉降的影响和土体各参数敏感性变化规律，需得到沉降量的精确解，考虑通过数值计算方法来得到地面沉降精确解，分析挡水构筑物对地面沉降的影响特征，并由 MATLAB编程和公式推导计算分析和验证挡水构筑物的设置对土体参数相对于地面最大沉降量敏感性的影响。

1 抽水沉降模型的建立

1.1 基于渗透固结理论的抽水沉降力学模型

比奥从固结机理出发，考虑土体三向渗流和变形，且考虑土体变形与孔压的相互作用，在太沙基固结理论的基础上推导了准确反应孔隙压力消散和土体固结关系的真三维固结方程[18](假设土体骨架微小弹性变形，变形符合压缩定律；地下水不可压缩，渗流符合达西定律)：

(1)

式(1)中，G为剪切模量，μ为泊松比，P为孔隙水压力，γw为4 ℃下水的容重，u、v、w为土层x、y、z向的位移，Kx、Ky、Kz为土层x、y、z向的渗透系数，η2为拉普拉斯算子。采用有限元法，以比奥固结理论为基础，通过构建地下应力场和渗流场耦合模型，研究挡水构筑物对抽水引起的地面沉降影响征。

1.2 抽水沉降的几何模型

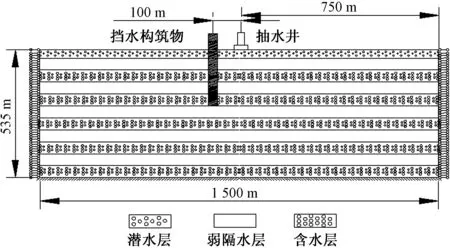
图1 计算模型示意图Fig.1 Schematic diagram of the calculation model

考虑多层含水层和弱隔水层时的计算模型如图1所示，由于一般情况下，地下土层一般为隔水层与含水层互层，由于出于规律性研究的考量，选取的土层不宜过少，但太多亦意义不大，结合文献[10,15]，分析模型由含水层与弱隔水互层的11个土层组成。出于定性研究的目的，地下挡水构筑物很少有深入到地下500 m的情况，且主要分布于从地表至地下200 m范围内，所以除地表土层外，其余地层选取为50 m厚，即包括1个35 m潜水层、5个厚度为50 m的承压含水层、5个厚度为50 m的弱隔水层。由于以边界不透水的工况为研究对象，研究对象应选为大范围，故模型长、高分别为1 500 m和535 m，厚度1 m。初始地下水位取5 m。模型侧面设为法向位移约束，底面设为全约束，表面为透水边界，侧面和底面均为不透水边界。开采井类型为排井，研究范围内只有一个且位于模型中间，方向与宽方向垂直。地下构筑物位于排水井左侧，为了避免挡水构筑物与周边土体由于材质不同而引起的应力分布变化对挡水效应的分析，本文计算过程中，地下构筑物相对于土层设为不透水材料。

1.3 计算参数

现结合一般实际情况，以文献[10,15]研究区域中各土层分布特征和相关土体参数大小为基础，以达到了解地下挡水构筑物对土体参数敏感性影响规律的研究目的。由于地表土层一般缺乏上覆荷载，故选为潜水含水层，岩性为粉砂。由于接近地表的土层，接收渗透雨水和地表水较多，第一隔水层选为黏土。起初，随着深度增大，在承压水的作用下，细粒颗粒被水流冲走，含水层构架颗粒增大，故选为细砂和中细砂，深处含水层由于承压加大，土层孔隙减小，水流变慢，含水层选为粉细砂。除接近地表的隔水层外，其余隔水层皆为粉质黏土。由于选取模型土层较厚，为了使模型与一般实际更吻合，隔水层皆设置为弱隔水层。具体各物理力学参数见表1。

计算模型包括不考虑挡水构筑物和考虑挡水构筑物两大类，在不考虑挡水构筑物时，计算开采层分别为第1～5含水层时的地面沉降；考虑挡水构筑物时，计算分析挡水构筑物各种进深工况时的影响，考虑到目前一般人类活动中，挡水构筑物进深、地下水开采深度及开采量等情况，设置开采层为第2含水层，抽水速度设置为40 m3/d。

2 抽水引起的地面沉降数值计算结果分析

土的压缩固结其实不仅与土体本身的性质有关，也与边界条件、抽水情况和人类活动等有关。条件不同，得到的结果往往有很大的差异。在地表处设置24个监测点，其中抽水井附近监测点较密。经相关研究，人类活动10 a左右为一个周期，故以下计算结果为开采含水层10 a后地面沉降的情况。

2.1 不设置挡水构筑物时地面沉降数值计算结果分析

由图2为不设置挡水构筑物时土体沉降云图，计算结果如图3，在没有挡水构筑物的情况下，抽取地下水引起的地面沉降量随着抽水层深度的增大而增大，开采第五含水层10 a后的最大沉降量达0.415 5 m，是开采第一含水层10 a后最大沉降量的2.61倍。地表沉降较为平缓，沉降差较小，最大沉降差发生在抽取第二含水层时，最大沉降差为0.041 3 m。分析认为这是由于模型边界不透水的设定和各含水层良好的透水性所致。

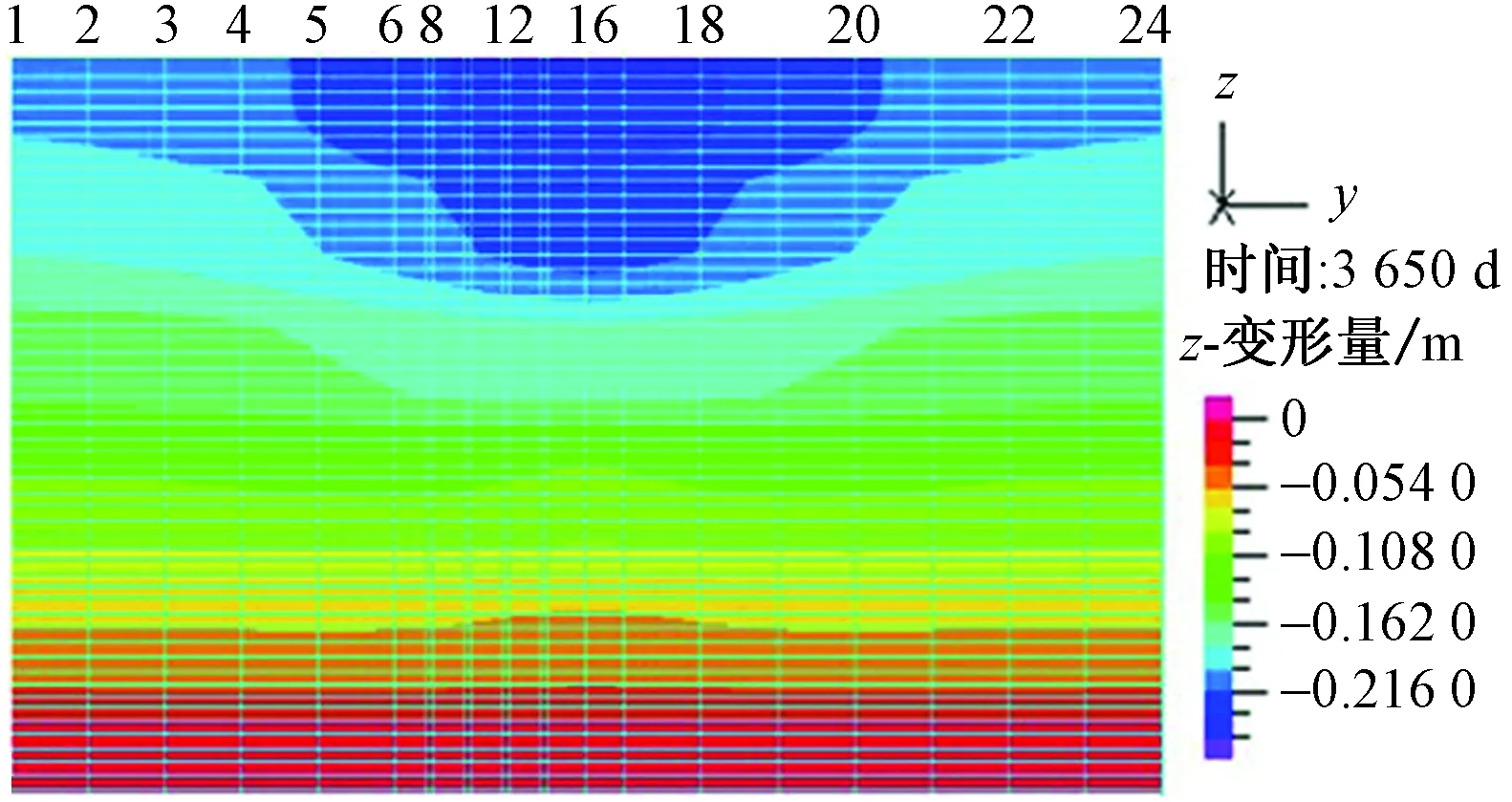
图2 不设置挡水构筑物时土体沉降云图Fig.2 Cloud diagram of land subsidencewithout water retaining structure

2.2 设置挡水构筑物条件下地面沉降数值计算结果分析

考虑挡水构筑物深度的影响时，将挡水构筑物设置在抽水井左侧距离水井100 m处，抽取第二含水层。考虑到抽水模型的対称性，且抽水井左侧挡水构筑物的设置对右侧的沉降量无影响，故只统计设置有地下挡水构筑物的抽水井一侧15个监测点的沉降，分析随着挡水构筑物逐渐深入地下时的地表沉降特征。

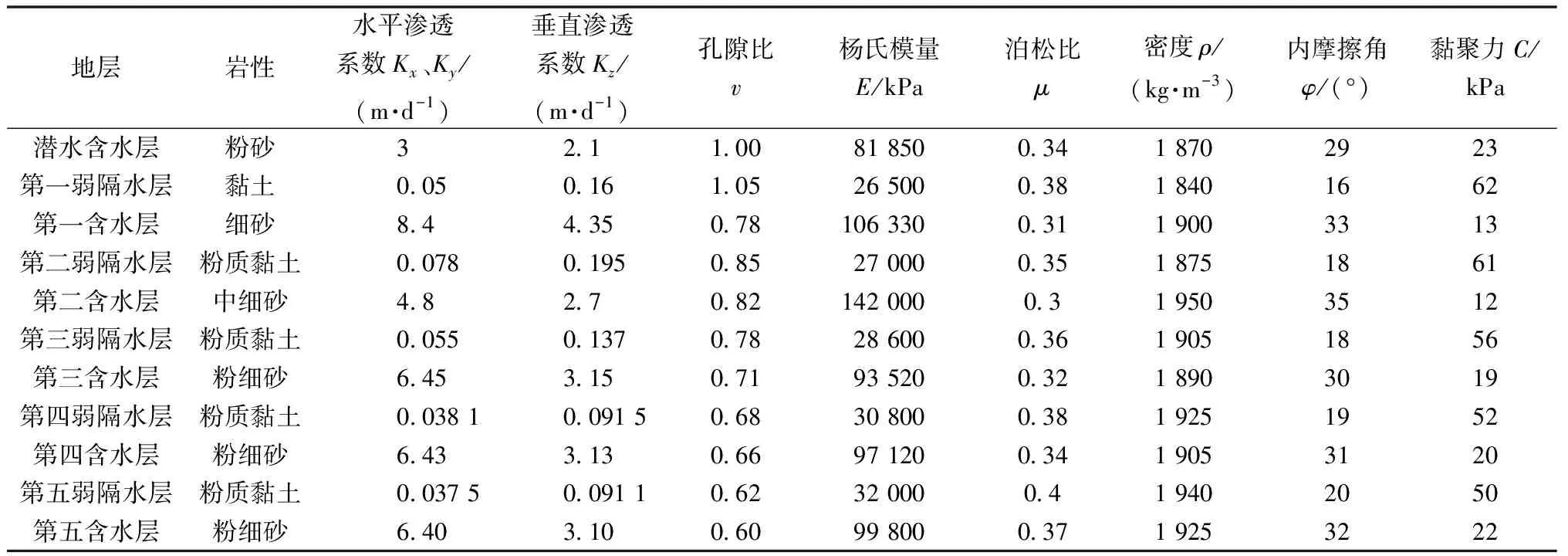
表1 各土层物理力学性质参数表Table 1 Parameters of physical and mechanical propertyof each soil layer

图4为设置挡水构筑物时土体沉降云图，计算结果如图5、图6所示：在抽水井处，地面沉降量随着挡水构筑物的深入逐渐增大，当挡水构筑物由未完全深入第二含水层底部的225 m处深入到第二含水层底部的235 m时，即由部分阻挡到完全阻挡抽水层时，地面沉降增幅最大，增幅达21.73%，其他情况下随着挡水构筑物深入地面沉降量增幅都较小。挡水构筑物另一侧，距离抽水井足够远的650 m处，如图6，沉降量起初随着挡水构筑物的逐渐深入小幅增大，随后深入到第二含水层底部时，沉降量出现较大幅度的减小，显示沉降量小于未设置挡水构筑物时，随着挡水构筑物的继续深入地下，沉降量呈现小幅减小趋势。结合前面介绍的抽取各含水层的沉降特点，结合图3可知，在650 m处起初随着挡水构筑物的入深，沉降量有小幅增大是由于挡水构筑物只挡住了浅部土层的透水，在没有全挡住抽水层之前却加大了深部土层的开采量，进而导致挡水构筑物刚开始深入地下时，650 m处沉降量小幅增大。总体来看，随着挡水构筑物的深入，地表沉降差增大。另外，在抽水井挡水构筑物附近，地表的沉降量也是随着挡水构筑物的深入逐渐增大，挡水构筑物深入到完全挡住抽水井另一侧时，即挡水构筑物深入地下535 m，在挡水构筑物处监测点，虽然在理论上地下水头减小量是降低，但比起未设置挡水构筑物时沉降量增大29.95%，分析表明这主要是由于抽水井一侧发生的较大沉降量增大地层侧摩阻力所致。

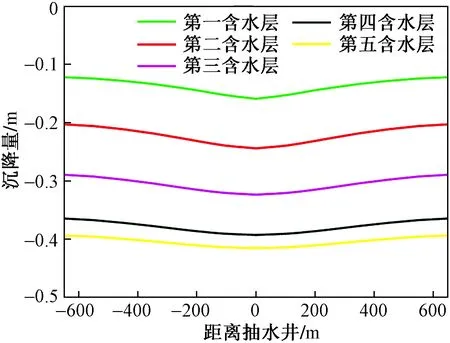
图3 开采不同含水层时地面沉降曲线Fig.3 Curves of land subsidence whenpumping different aquifer

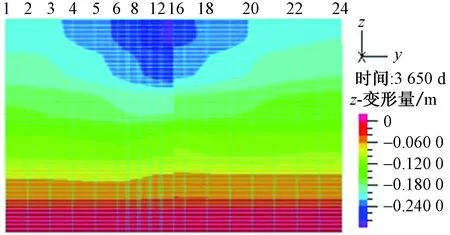
图4 挡水构筑物深入到第二含水层底部时抽水土体沉降云图Fig.4 Cloud diagram of land subsidence with water retainingstructure penetrating to the bottom of the second aquifer

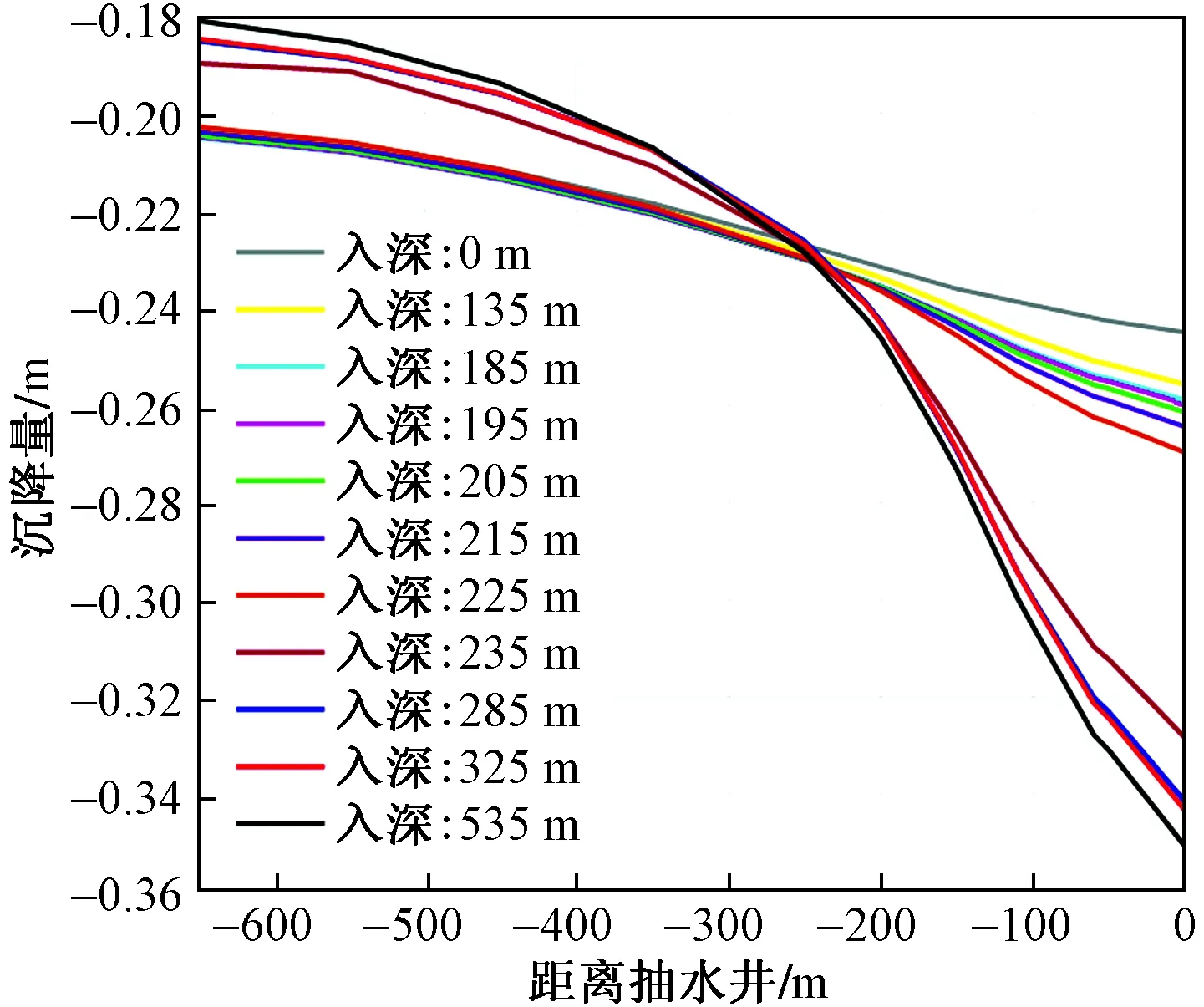
图5 设置挡水构筑物一侧不同挡水构筑物入深条件下抽水引起的地面沉降曲线Fig.5 Curves of land subsidence caused by pumping water onthe side with water retaining structure which penetratinginto underground differently

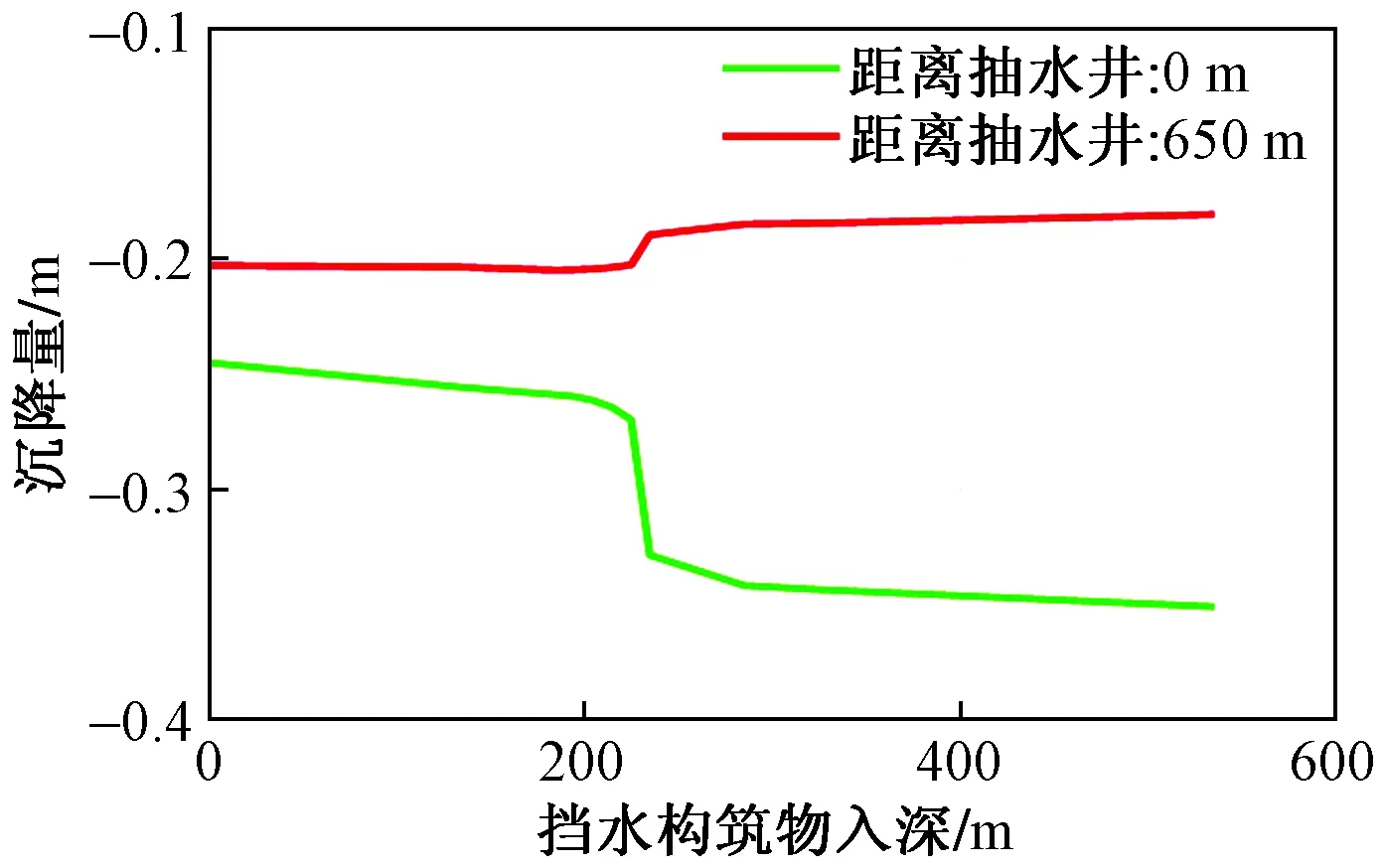
图6 随着挡水构筑物深入地下两典型监测点沉降曲线图Fig.6 Curves of land subsidence of two typicalmonitoring points with water retaining structurepenetrating into underground

3 基于二次响应面法的最大地面沉降土体参数相对敏感性和结构可靠度分析

3.1 二次响应面法理论

对大型复杂的结构进行计算分析时，采用传统的解析法得到结构的显式函数往往很困难，而且推导得到的函数在应用上一般均具有限制性和近似性的特征。这种情况下，不改变原有方程的含义，在概率意义上又能代替显示函数的多项式响应面法应运而生[19]。多项式响应面法是通过一系列数值模拟计算,采用多项式函数拟合未知的极限状态面。其中分析结构非线性函数的不含交叉项的二次多项式响应面函数得到广泛应用，亦选取此种方法：

(2)

式(2)中:Xi为与函数值有关的参数样本点，系数a、bi和ci由选取2n+1个样本点来获得。

3.2 结构可靠度JC算法

地下土体的复杂性决定了土体参数往往不能准确获取，基于土体随机变量分布参数来获得的结构可靠度具有较好的现实意义。

JC算法又称验算点法或改进的一次二阶矩法，是在中心点法的基础上考虑了变量的概率分布，正态分布变量需转化为等效正态分布[20]。采用结构在验算点处的切平面代替极限状态曲面，并利用改进的一次二阶矩法计算结构可靠度。结构极限状态功能函数可表示为

Z=g(X1,X2,…,Xn)

(3)

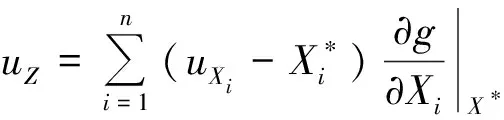
(4)

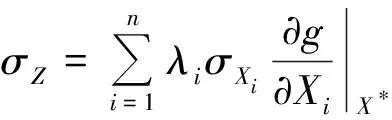
(5)

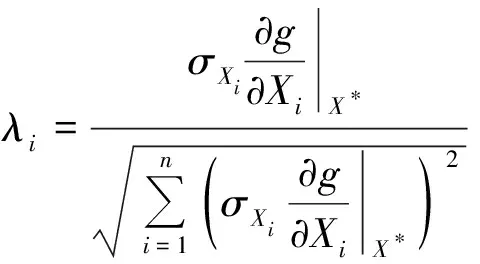
(6)

由可靠度定义有

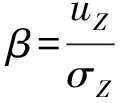
(7)

结合式(4)～式(7)可得

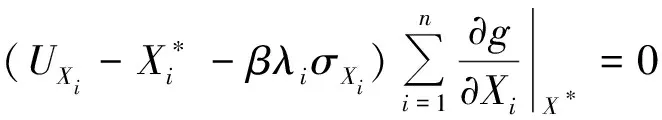
(8)

满足这方程式的验算点为

(9)

二次响应面法新验算点

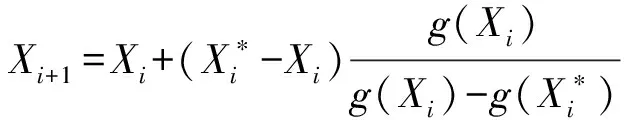
(10)

式(10)中：Xi为JC算法初始迭代点。

3.3 土体参数相对敏感度计算方法

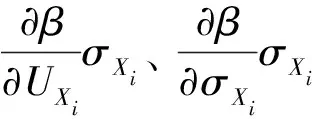
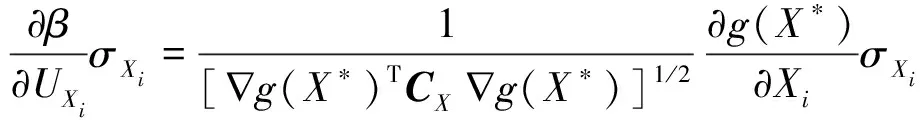
(11)

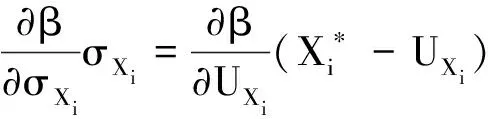
(12)

式中:UXi和σXi分别为随机变量分布参数的均值和方差，X*为随机变量分布参数X的验算点，CX=σXρXσX，为随机变量分布参数X的协方差矩阵，ρX是相关系数矩阵。

3.4 最大地面沉降土体参数相对敏感度和结构可靠度计算结果分析

选取无挡水构筑物和设置挡水构筑物深入地下235 m，即正好完全阻挡第二含水层两种典型工况，分别开采第一含水层、同时开采第一、二含水层和开采第二含水层的三组工况为对比研究对象。

工况一：无挡水构筑物，开采第一含水层。

工况二：挡水构筑物深入地下235 m，开采第一含水层。

工况三：无挡水构筑物， 等量开采第一、二含水层。

工况四：挡水构筑物深入地下235 m， 等量开采第一、二含水层。

工况五：无挡水构筑物，开采第二含水层。

工况六：挡水构筑物深入地下235 m，开采第二含水层。

各参数分布特征的选取结合文献[22]而得，随机变量分布参数的均值由各土层设计值加权得到，如表2所示。

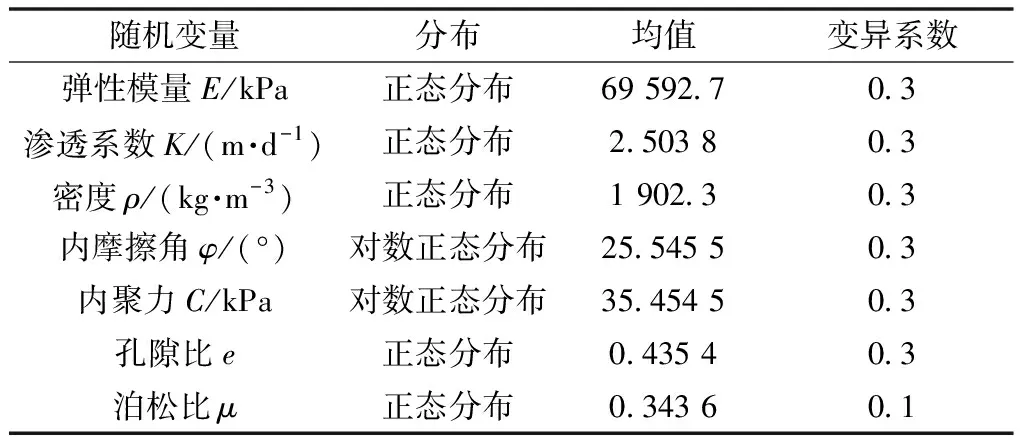
表2 敏感性分析的土体参数Table 2 Soil parameters for sensitivity analysis

考虑弹性模量和渗透系数两个最敏感参数间相关性，ρ(E,K)=-0.2,ρ(E,K)=0,ρ(E,K)=0.2，其他参数互相独立。

由于选取抽水含水层较厚，计算结构可靠度的最大沉降量选取不宜过小，结合规范可知，一般工程中允许最大地面沉降量为0.2 m左右,且实际情况中互层地层概化后一般为10～20 m，出于选取地层厚度及前面计算得出地表沉降量的考虑，计算参数相对敏感性和结构度时，设置最大允许地面沉降为0.8 m。利用二次响应面法、JC算法，MATLAB编程计算参数相对敏度和结构可靠度的具体计算流程如图7。

计算结果如表3所示：对比同一工况下的参数敏感度可知，影响地面沉降的参数按敏感性大小排序依次是E、K、μ、ρ、φ，其中C和e敏感性极小，E、K、μ对沉降量的敏感性占绝对地位。φ的敏感性大于C的原因推测是开采的含水层是深层，侧限土压力较大；而e从无到有的变化可能与开采深度有关。对比工况一和二，工况三和四，工况五和六，分析可知，当开采含水层相同时，E、ρ和e敏感性均随挡水构筑物的设置敏感性减小，而K、μ、φ和C增大。

地面沉降由剪应变和正应变两项控制，而由剪切应力公式：

τ=kρghtanφ+C

(13)

式(13)中:g是重力加速度，k为侧压系数，k=μ/(1-μ),由于密度ρ与正应力相关：

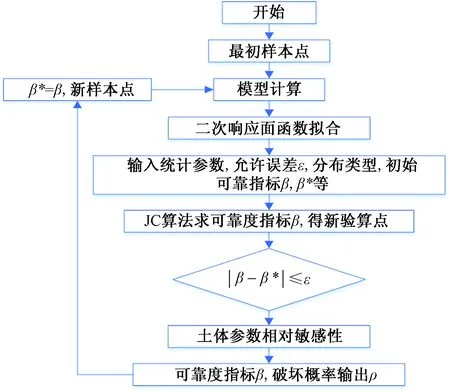
图7 土体参数相对敏感度和结构可靠度计算流程图Fig.7 Flow chart of parameter sensitivity andstructure reliability calculation process

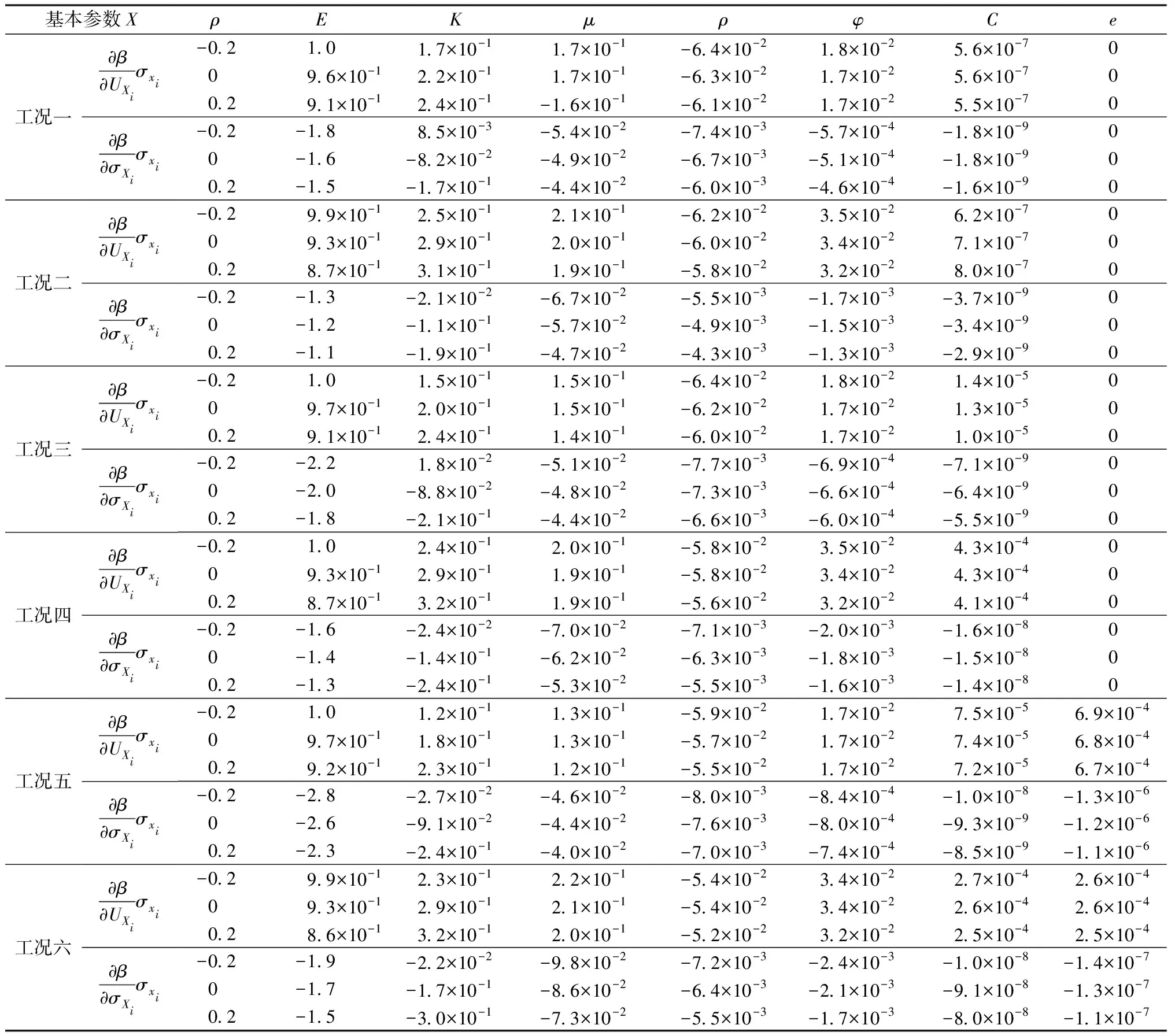
表3 土体参数相对敏感度计算结果Table 3 Computing results of relative sensitivities of soil parameters

σ=ρgh

(14)

且由于发生变形沉降过程中S(σ)>S(τ),可知与剪应变即侧摩阻力控制地面沉降量正相关的参数有泊松比、摩擦角和内聚力，由此可见，挡水构筑物的设置，使得由土层侧摩阻力控制的沉降比例提高，侧摩阻力的重要性增大,与前述数值模拟地面沉降规律分析一致。

对比工况一、三和五、工况二、四和六无法得出明显规律，即环境相同，开采含水层不同时，未发现明显规律。

为了验证敏感性参数分析的正确性，进一步计算所有随机变量分布参数变异和部分随机变量分布参数变异对可靠指标结果的影响。计算结果如表4所示。

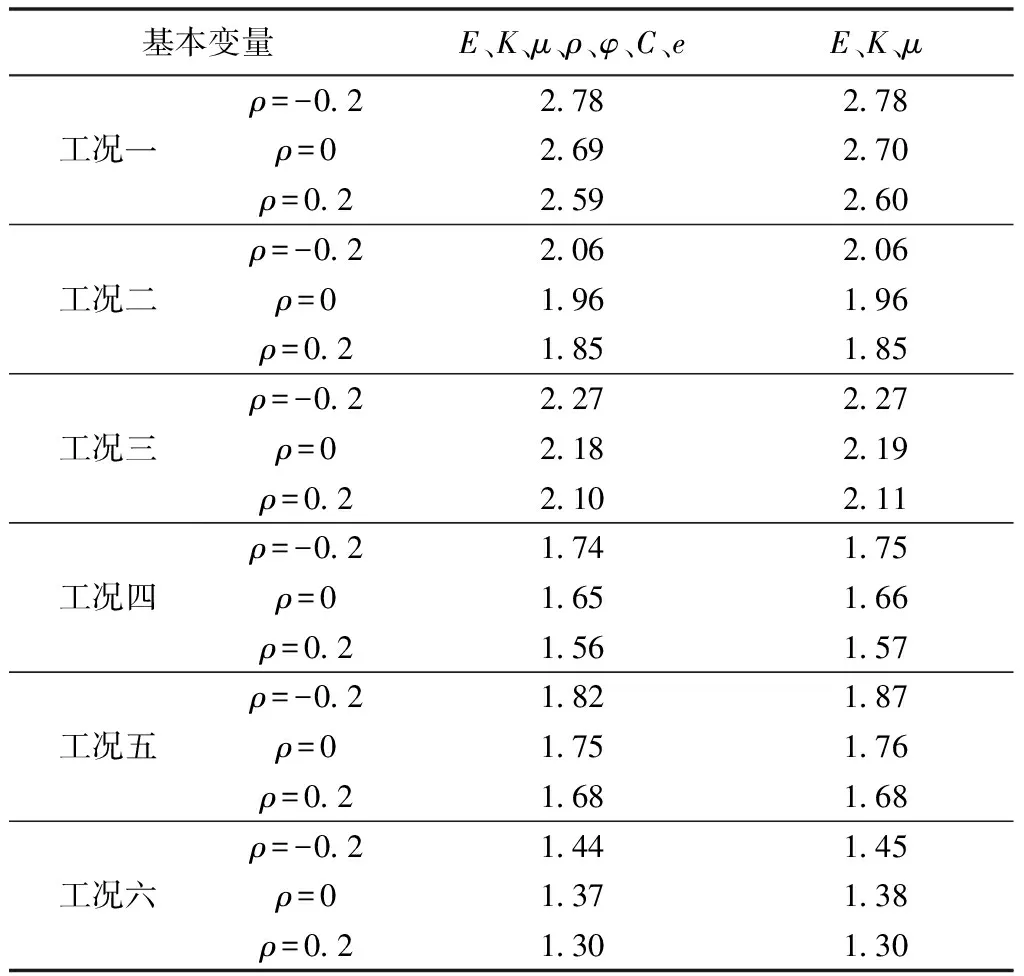
表4 考虑不同变量的结构可靠度Table 4 Structure reliability considering different variables

从表4可以看出，只考虑参数弹性模量、渗透系数、泊松比的变异与考虑全部参数变异得到的可靠度指标基本一致，进一步验证了这三个参数对地面沉降影响较大的分析结果。倘若工程级别较低，地面沉降可靠度的计算可视其他参数为常数，以便减小不必要的工作量。同时，由计算结果可知，考虑弹性模量与渗透系数的正相关性和设置挡水构筑物，计算所得的可靠度指标均减小，设置挡水构筑物的影响与前述数值模拟结果一致。

4 考虑地面沉降侧摩阻力的二维控制方程推导验证土体参数敏感性变化

地下土体是一个整体，不同位置的各点变形量具有关联性和传递性，特别是存在沉降差的相邻两点。因而由开采地下水而导致每一个土体微单元的固结压缩量不仅与该单元孔隙水压力消散导致有效应力增加有关，当与周围单元体存在沉降差时，还受到周围土体牵引而导致的有效应力减小有关。

考虑侧摩阻力，基于假定①各土层土体均质、各向同性，和假定②土体只发生竖向位移、土体应力应变关系符合线性关系。进行理论推导[23]，开采地下水引起的土层压缩公式为

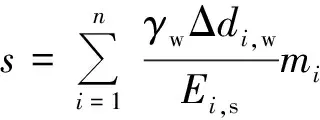
(15)

式(15)中：n为水头发生变化的土层数，Δdi, w是土层i水头减小量，γw为地下水重度，mi为土层i厚度，Ei,s为弹性模量。

考虑侧摩阻力径向传递时，选取单位长度微元体进行分析：

(16)

式(16)中：τ、τrz为土层剪应力，r是土体与抽水井之间的距离。

由剪应力、剪应变和位移的关系，可知：

τrz=Gγrz

(17)

(18)

式中：G为剪切模量，γrz为总剪应变,ur和s分别为r和z方向上的位移。

当忽略影响非常小的径向位移，只考虑竖向沉降时，有：

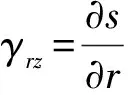
(19)

联立式(16)和式(19)可得：

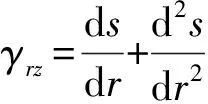
(20)

由侧摩阻力控制的沉降量为

(21)

式(21)中：M为抽水影响的地下深度。

增加的剪应力，即侧摩阻力对地面沉降有抑制作用

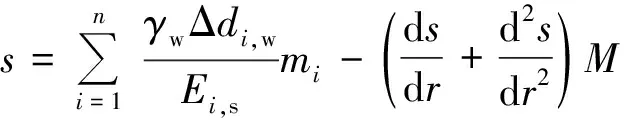
(22)

由于二次导项较小，此处可以不予考虑可得

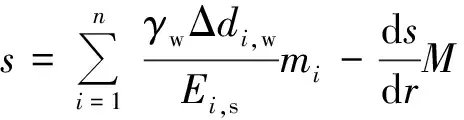
(23)

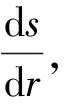
所以控制方程的分析结果与敏感性参数分析结果一致，再一次验证了挡水构筑物的设置会增大渗透系数K和与侧摩阻力相关的参数泊松比μ、内摩擦角φ和内聚力C敏感性，相应地其他参数敏感性会减小的结论。

5 结论

(1)在未设置挡水构筑物时，开采地下水时地表沉降差均较小，但是随着开采含水层深度增加，地表沉降量增大。

(2)随着挡水构筑物逐渐深入地下，挡水构筑物两侧的沉降规律有所不同，开采井一侧地表沉降为逐渐增大，另一侧为先增大后减小，沉降量变化幅值较小；但不论挡水构筑物深入地下多少米都会加大地表最大沉降量和沉降差，其中挡水构筑物对开采层的挡水效应所引起的地面沉降最为显著。

(3)对地面沉降有影响的参数按敏感性大小排序依次是弹性模量、渗透系数、泊松比、重度、内摩擦角，其中内聚力和孔隙比敏感性极小，弹性模量、渗透系数、泊松比对沉降量的敏感性占绝对地位。

(4)挡水构筑物的设置会加大渗透系数和与侧摩阻力相关参数的敏感性，与侧摩阻力相关的参数有泊松比、内摩擦角和内聚力，相应地其他与正应变相关的物理力学参数，如弹性模量、密度和孔隙比敏感性减小。故当计算分析地面沉降量时，应该适当适时考虑土层侧摩阻力的影响。

(5)以最大沉降量为结构可靠指标，地下挡水构筑物的设置和考虑弹性模量与渗透系数的正相关性计算得到的结构可靠度均降低。土层由侧摩阻力控制的沉降量大小主要取决于土层的沉降差和发生变形的土层厚度。