采用熵产理论的离心泵断电过渡过程特性

冯建军，张 钰，朱国俊，李昀哲，李文锋，罗兴锜

采用熵产理论的离心泵断电过渡过程特性

冯建军1，张 钰1，朱国俊1※，李昀哲2，李文锋2，罗兴锜1

（1. 西安理工大学水利水电学院，西安 710048；2. 浙江富安水力机械研究所，杭州 311121）

该文对商业软件ANSYS CFX进行二次开发，通过自定义函数求解角动量方程获取实时转速，建立了模拟离心泵事故断电过渡过程的三维瞬态数值计算方法，获得了离心泵外特性参数瞬变规律以及内部流场的动态特性。进一步采用熵产理论获得了离心泵事故断电停机飞逸过程中过流部件流场能量损失分布情况，并对流场内随时间变化的能量损失进行定量评估。结果表明：在整个事故断电飞逸过程中，熵产与离心泵外特性之间存在着明显的相关性，能量损失的产生与流场内部的流动分离、回流、漩涡等不良流动现象相关；叶轮、导叶与引水管的主要损失均是由湍流耗散引起的，其壁面熵产占总熵产的10%～15%左右，不可以忽略，而蜗壳区的损失则主要是由近壁面处的强壁面效应引起的；通过分析各部件流场局部熵产率分布随时间的变化情况，可以得出在制动工况中内流场的高损失区域最大。

离心泵；流场；数值模拟；断电飞逸；熵产；瞬态特性；能量损失

0 引 言

离心泵具有结构紧凑、适用范围宽等优点，广泛运用于液体输送、冷却系统等工业设备。近年来，随着泵在工程应用领域的不断投入运行，泵的快速启动、事故断电停机、快速启闭阀门等瞬态过程时有发生。在这些过程中，泵的转速、流量等外特性参数会在短时间产生剧烈的变化，使得内部流场极为不稳定，流体的湍流强度急剧上升，泵内流体经历了边界层的形成、流动分离、漩涡等不稳定流动现象，与稳定工况中产生的周期性非定常流动相比存在很大的区别，即产生一定程度的瞬态效应[1]。因此，对离心泵瞬态流动与快速瞬变过程的研究得到了越来越多的关注。

目前国内外对于泵瞬态过程的研究主要集中在启动过程方面，大部分采用的是试验与数值模拟相结合的方法。国外最早是日本学者Tsukamoto等[2]对一离心泵进行了快速启动与停机实验研究，对瞬态外特性结果进行了分析。在国内，吴大转等[3]对离心泵快速启动外特性、不同管路阻力进行了实验研究。李志锋[4]分别对不同加速度、不同稳定转速和不同管路阻力条件下的离心泵启动过程进行试验研究，采用循环管路系统模型对全流场进行了非定常流动计算。李伟[5]通过观察斜流泵启动过程的内部流场演化过程，探究了斜流泵启动过程瞬态效应对内部流场涡结构与压力脉动等外特性的影响。

离心泵启动过渡过程方面的研究比较丰富[2-5]，但对于泵停机方面尤其是事故停机的研究相对较少。张玉良等[6]通过建立包含离心泵在内的循环管路系统对停机过程进行自耦合的数值模拟计算，分析了低比转速离心泵在停机过程中的瞬态特性与内流场的非定常流动。周大庆等[7-8]对轴流泵模型断电过程进行数值模拟，得到了机组转速、流量、转矩等参数随时间的变化规律，以及截面流速场、叶轮叶片压力场的演变过程。金国栋等[9]对不同叶片角度的泵进行断电飞逸特性试验，获得其单位飞逸转速，并对其内部流场特性进行分析讨论。苟东明等[10]采用全三维耦合过渡过程研究方法对泵断电飞逸过渡过程进行分析计算，获得了不同时刻流场的演变过程。可以看出目前对于停机这一瞬态过程的研究对象大部分为轴流泵或水泵水轮机，而对离心泵的停机尤其是事故断电飞逸过程的研究尤为不足，且目前的研究内容主要围绕机组的瞬态外特性以及内流场的非定常流动展开，针对泵瞬态过程中能量损失分析评价方面的研究很少。

对于能量损失的分析，传统的方法是通过内部流场的压力、速度及其分布的情况，间接地获得水力损失的范围和大小，但不能直观获取能量损失具体发生的部位，说服力有所欠缺。而今越来越多的学者开始关注流动中的能量损失与熵产的联系[11-14]，然而熵产理论在流体机械方面运用较少。Li等[15]基于熵产理论对一单级离心泵的扬程-效率曲线中的不稳定特征进行分析，探究出其不稳定的产生机理。Pei等[16]利用熵产法对一水泵叶轮与导叶之间的轴向间隙所产生的能量损失进行了分析评价，得到湍流耗散是产生内流损失的主要原因。Gong等[17]利用熵产理论分析了混流式水轮机的水力损失分布情况，进一步表明了熵产分析法的优势。Li等[18]针对水泵水轮机模型对不同导叶开度进行熵产损失的对比分析，并考虑熵产的壁面效应，提出计算壁面熵产损失的方程，解决了计算损失存在较大误差的问题。张亚太等[19]采用熵产理论对二维水翼空化流场中的能量损失做出分析。Yang等[20]通过熵产方法从能量的角度阐明了高速离心泵诱导轮与叶轮之间时序效应的形成机理，对泵内能量损失做出了分析评价。Chang等[21]利用熵产理论对不同叶片厚度条件下的水力损失大小、位置与类型进行了系统的分析，为叶片厚度的合理设计提供了理论基础。以上研究结果均表明流场内部流动中的损失可以用熵产进行评价与分析，且可以直接显示内部流场中水力损失值大的区域，定量的描述能量损失的大小，具有非常明显的优势。

为了准确掌握离心泵在事故断电停机飞逸过程中的内外特性以及能量损失情况，本文采用熵产理论分析该过程中各过流部件流场能量损失发生的位置与大小，进一步探究能量损失产生机理以及内外特性瞬时变化之间的关系。

1 计算模型与方法

1.1 模型与计算参数

以某泵站的模型离心泵作为研究对象，其三维几何模型如图1所示。计算采用的初始参数如表1所示。

图1 离心泵几何模型

表1 计算工况参数

1.2 网格划分

本文利用ANSYS ICEM软件对各过流部件进行结构化六面体网格划分。计算域由蜗壳、导叶、叶轮和引水管组成，各部件网格如图2所示。

图2 各过流部件网格

1.3 网格无关性验证

对于同一模型来说，网格数量是影响数值模拟精度的关键因素之一，本文选取4种不同数量的网格数对离心泵在=0.222 3 m3/s，=1 200 r/min这一工况下进行三维定常湍流计算，以扬程和效率为目标函数进行网格无关性验证。如图3所示，扬程和效率随着网格数的增加而变化，当网格数量在620万以上时，扬程与效率几乎保持不变，故最终选择网格数量为620万。

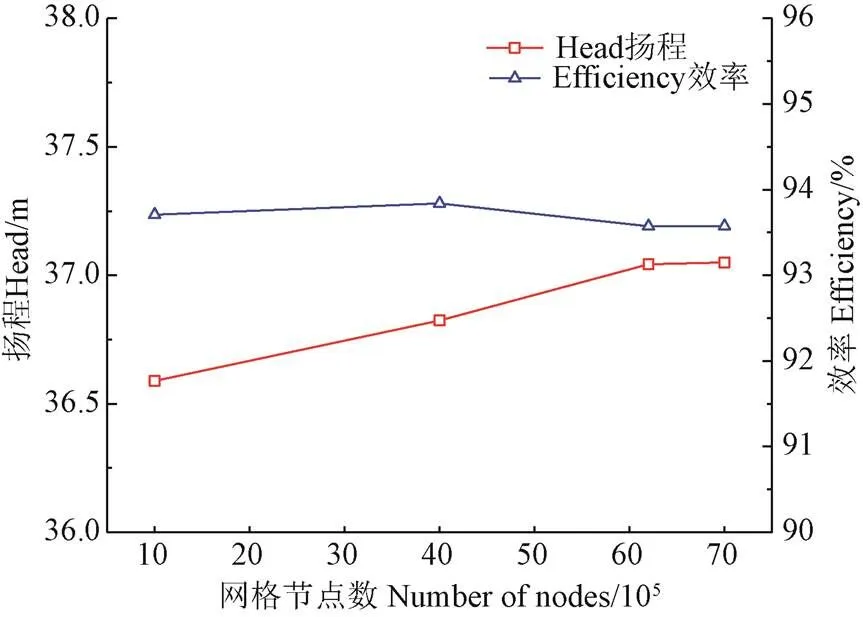
图3 网格无关性验证

1.4 边界条件设置

采用CFD（computational fluid dynamics）商业软件ANSYS CFX18.0对模型离心泵事故断电飞逸过程进行数值模拟，采用剪切应力传输模型（shear stress transfer，SST）-湍流模型。瞬态计算时需要利用对应的稳态工况的定常计算结果作为起始边界条件，本次计算中进出口的边界条件类型均设置为Opening。其中，将蜗壳计算域的边界条件设置为对应的定常结果的出口总压值，将引水管计算域的边界条件设置为对应的定常结果的进口静压值。计算域中仅将叶轮区域设为旋转域，其余三个部件均设为静止域，旋转域与静止域之间的采用“Transient Rotor Stator”交界面，各个过流部件的壁面均设置为无滑移壁面。时间步长设为0.000 5 s。

1.5 算法实现

基于ANSYS CFX软件，通过添加用户自定义程序User Fortran对软件进行二次开发，对整个停机过程的转速、转矩等参数进行控制和计算。此程序是根据转动平衡方程控制力矩、转速的动态迭代和变化的过程，转动平衡方程如下

式中M为作用在叶轮上的合力矩，N·m；为系统的负载力矩，N·m；为叶轮的转动惯量，kg·m2；为叶轮旋转的角速度，rad/s；为时间，s。

由于离心泵事故断电后不带负载，所以=0，即任意时刻叶轮的旋转角速度为

（2）

1.6 数值模拟与试验对比

模型试验是检验数值模拟准确性的重要方式之一，相应的模型试验装置和模型叶轮如图4a和图4b所示。

图4 试验装置及模型叶轮

对离心泵模型在1 200 r/min下的不同流量工况进行数值计算，并与模型试验结果进行对比，如图5所示。从图中可以看出，效率模拟值略大于试验值，这是由于在数值模拟计算中忽略了间隙和圆盘损失等因素。在整个计算范围内，数值模拟结果与试验结果得到的外特性关系曲线规律是一致的，所以可认为数值模拟的结果是可靠的。

注：H/H0为无量纲扬程，η/η0为无量纲效率，Q/Q0为无量纲流量。

2 熵产理论

熵增原理是热力学第二定律的其中一种表述，即不可逆过程中熵的微增量总是大于零。熵产是指过程中不可避免地存在由不可逆性所造成的效应，使损失的机械能转化为内能。在离心泵事故断电飞逸过程中存在各种不良流动，如漩涡、流动分离、回流等，这些紊乱的流态会导致损失增加，从而引起熵产的增加；除此之外，动能、压力能转化为内能会产生耗散，也会引起熵产的增加。在本次计算中，由于水的比热容较大，可以认定在此过程中温度不变，故不考虑传热引起的熵产。

由平均速度引起的熵产率为

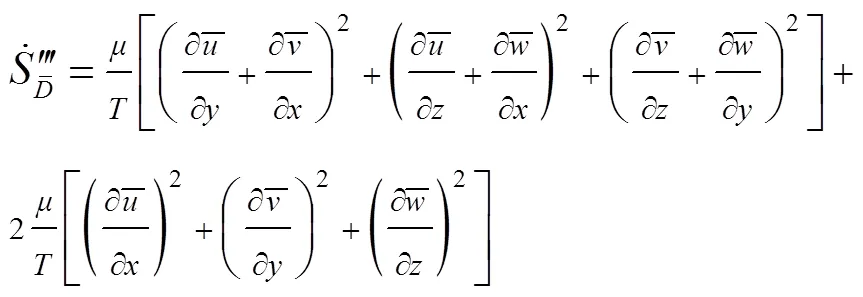
由脉动速度引起的熵产率为

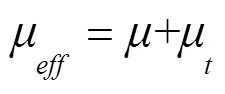
但是脉动速度分量在雷诺平均方程中是无法计算求得的，本文采用SST-湍流模型。故由脉动速度产生的熵产率可以用下式近似计算

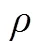
Herwig和Kock[23-24]发现，上述两部分熵产率都存在壁面效应，若在近壁面附近直接采用上述熵产率公式计算则会引起较大误差。张翔等[25]给出了对壁面摩擦损失的计算方法，单位面积局部壁面熵产率的计算公式如下

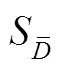
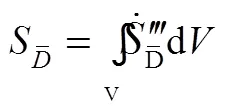
因此整个计算域内的主流区熵产为

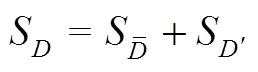
整个计算域内的总熵产为

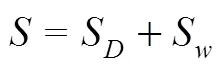
3 结果与分析

3.1 外特性变化规律

图6为离心泵在事故断电飞逸过程中的转速、流量以及转矩这三个外特性参数的相对值0、0和0随时间的变化规律。从图中可以看出：离心泵在事故断电后历经水泵工况、制动工况、水轮机工况以及飞逸工况。其中，在=0～0.114 5 s中处于水泵工况，各参数相对值迅速下降，转速下降至初始转速的45%，流量也随之减少，在=0.098 5 s时流量降为0，此时0到达波谷。此后离心泵进入制动工况（=0.114 5～0.211 5 s），正向流量逐渐减小，反向流量逐渐增大，转速继续下降，在=0.211 5 s时，转速降至0，此时0=-0.95，0=0.94。随后机组进入水轮机工况（=0.211 5～0.836 5 s），叶轮开始反向旋转，转速由0开始逐渐反向增大而后略有减小最后趋于飞逸转速。可以看到，在=0.28 s时转矩相对值达到最大值（0=1.22）后开始减小，当转矩稳定在=0附近时，离心泵就进入稳定的飞逸工况（>0.836 5 s），此时转速大小为初始转速的1.31倍，流量大小为初始流量的63%。

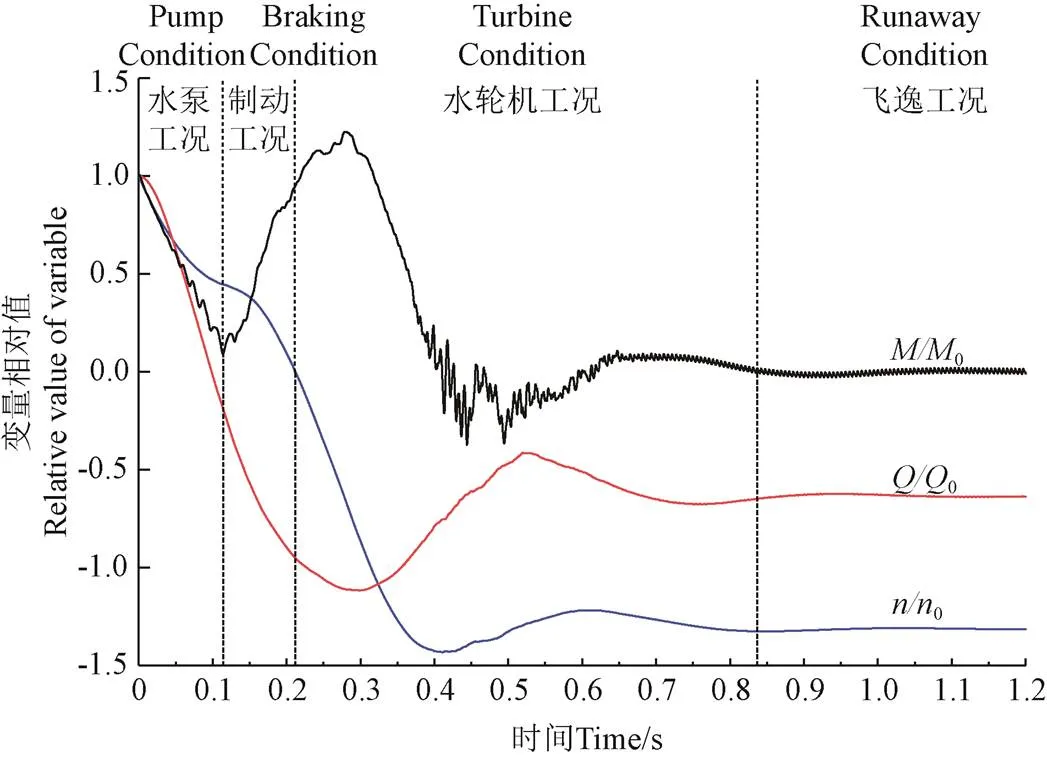
注：M/M0为转矩相对值；n/n0为转速相对值；Q/Q0为流量相对值。

3.2 各过流部件的熵产

图7 主流区熵产与壁面区熵产

离心泵在事故断电后的整个过程中各个过流部件包括叶轮、引水管、蜗壳、导叶的总熵产变化情况，如图 8a所示。由图可知，叶轮区域的总熵产值的变化幅度最大，这是因为断电后的叶轮做功能力下降，由于流量与转速的大小、方向的不断变化，导致其流道内的流态十分紊乱，存在漩涡、流动分离、回流等不良流动，引起速度梯度的不断变化，从而引起熵产值的大幅度变化；引水管的变化相较于叶轮来说熵产值变化幅度较小；而导叶区域在反向转速达到最大值时，熵产值出现明显突增，呈指数增加，这说明在接近飞逸转速时，导叶中出现的水力不稳定现象所产生的的动载大大增加；蜗壳的熵产数值小且几乎无变化，约占总损失的0.5%。在进入稳定的飞逸工况后（> 0.836 5 s），可以看到最大的熵产部件为导叶，其次是叶轮、引水管、蜗壳。

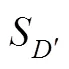
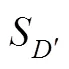
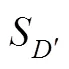
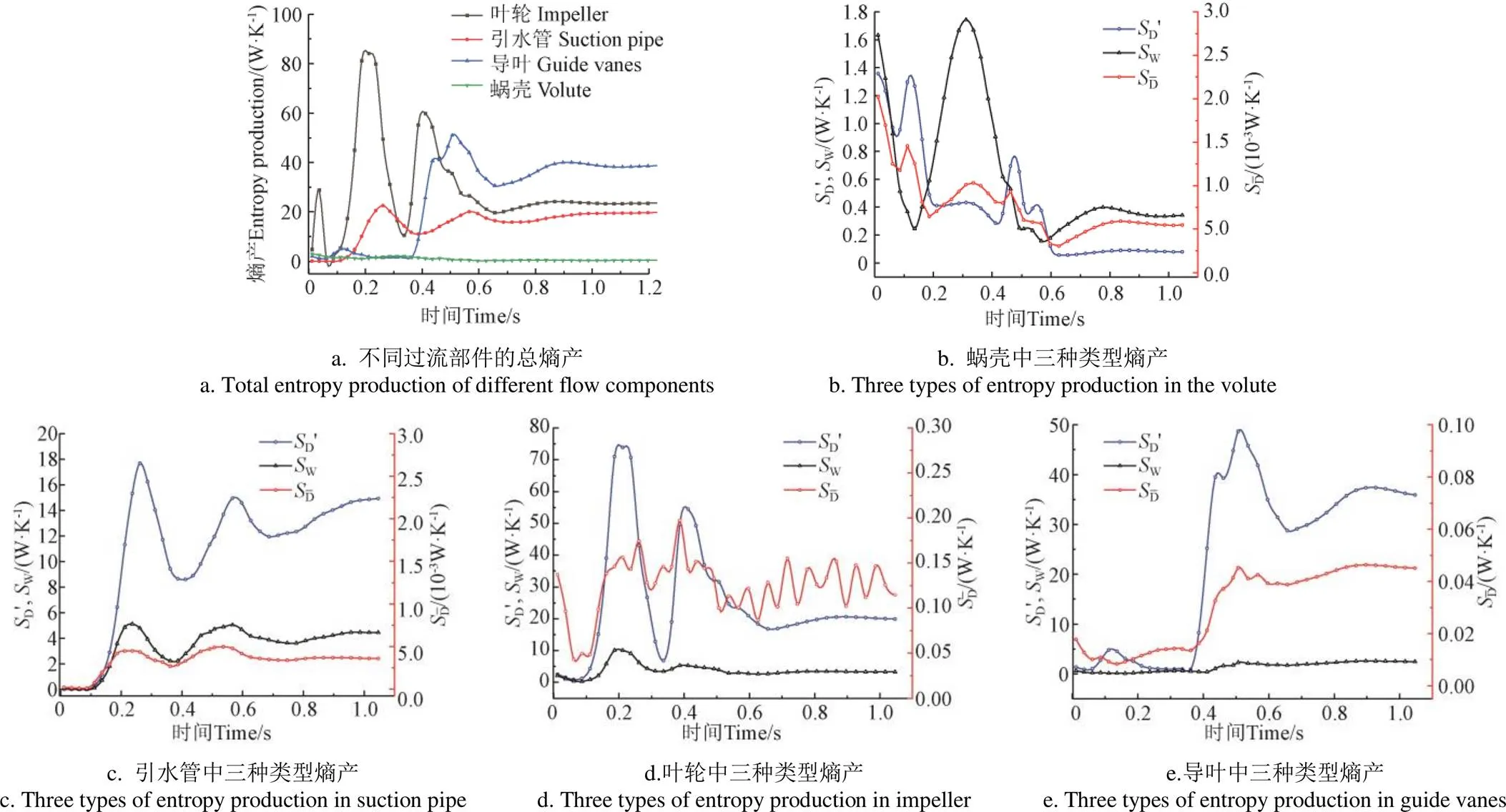
注:为直接耗散熵产；SD′为湍流耗散熵产；Sw为壁面熵产。

3.3 流场中的熵产分析

对事故断电飞逸这一过程结合叶轮与导叶在Span0.5叶片高度下的叶片展开截面的局部熵产率分布情况进行分析。

图9a为水泵工况与制动工况的临界工况点，此时转矩为此阶段的波谷，由图可以看出，小区域的高局部熵产率在此临界工况点之前主要集中在近隔舌处的导叶流道、叶片压力面以及叶轮叶片尾缘处，同时在叶片吸力面靠近前缘处也出现较高的局部熵产率。结合图8d、图8e可知，在转矩开始增大之前，湍流耗散熵产随着时间推移正向流量的减少而增大，即随着正向流量的减少，叶轮与导叶流场中的水力损失逐渐增大。产生上述现象是因为随着正向流量的不断减少，转矩不断减小，加之这个过程中的转速较高，内部流态紊乱，尤其在靠近隔舌处的流体流向紊乱，此时的水力损失的主要来源是流动分离，流动分离导致叶片表面的低流速运动与主流区的高流速运动进行较强的动量交换从而产生高水力损失。

随着反向流量不断增大，=0.161 5 s（图9b）时离心泵已进入制动工况，叶片吸力面的高局部熵产率区域逐渐发展扩大，且靠近叶片前缘处的高局部熵产率区域逐渐扩散消失，这是由于从叶片前缘进入叶轮的正向流量变小，从而与反向流量的混掺减弱，损失减小。

图9c为=0.211 5 s时（=0）局部熵产率分布情况，此刻为制动工况与水轮机工况的临界工况点。当转速=0时，高局部熵产率区域几乎充满整个流道，说明此时水力损失很严重。

图10给出了叶轮和导叶到达最大反向转速时刻的局部熵产率分布图与涡量云图。=0.411 5 s时，叶轮转速达到最大反向转速，此时的转矩接近于0，即将进入飞逸工况，内部流态较为紊乱，高局部熵产率区较大，且主要集中在无叶区以及叶片压力面靠近叶片尾缘处（此时的进水侧）。对比图10a与图10b可知：流场中涡的分布区域与高局部熵产率分布区域相似，说明流场由于受到流动分离等不稳定因素的影响而产生非定常涡等非定常现象，会造成流场中水力损失的增大，这也进一步表明了采用熵产分析流场能量损失的可靠性。

图11为叶轮与导叶进入稳定的飞逸工况后的局部熵产率的分布情况。在转矩、流量、转速的大小和方向等各参数均趋于稳定后，流场中的水力损失较小且分布均匀，此时只在离心泵叶片尾缘压力面以及导叶尾迹区域出现局部较高的损失区域，且由于转速过大，加上机组过流部件中出现的水力不稳定现象所产生的动载大大增加，从而引起过流部件的破坏与振动，威胁泵站的安全。

图9 不同时刻叶轮和导叶中局部熵产率分布

图10 t=0.4115 s（叶轮最大反向转速）的局部熵产率分布图与涡量云图

Fig.10=0.4115 s (maximum reverse speed )Entropy production rate and vorticity distribution in the impeller and guide vanes

图11 稳定的飞逸工况局部熵产率分布

4 结 论

本文基于熵产理论对离心泵断电飞逸过程中各个过流部件的熵产进行了分析，从能量的角度探究了不良流动的产生机理。通过对计算结果的分析，得到以下结论：

1）整个事故断电飞逸过程中，熵产与离心泵外特性之间存在着明显的相关性，在流量、转速与转矩发生突变的时刻，熵产也同时发生着剧烈的变化，能量损失的产生与流场内部的流动分离、回流、漩涡等不良流动现象相关。

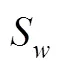
3）通过对叶轮与导叶的局部熵产率在不同阶段工况的分布情况进行分析，从能量的角度直观地得到在制动工况中内部流场的高损失区域最大，到转速=0的时刻高损失区域充满整个叶轮流道。

[1]郑源，张健. 水力机组过渡过程[M]. 北京：北京大学出版社，2008.

[2]Tsukamoto H, Ohash H. Transient characteristics of a centrifugal pump during starting period [J]. ASME Journal of Fluids Engineering, 1982, 104(1): 6－13.

[3]吴大转，王乐勤，胡征宇. 离心泵快速启动过程外部特性的试验研究[J]. 工程热物理学报，2006(1)：68－70. Wu Dazhuan, Wang Leqin, Hu Zhengyu. Experimental study on explicit performance of centrifugal pump during rapid starting period [J]. Journal of Engineering Thermophysics, 2006(1): 68－70. (in Chinese with English abstract)

[4]李志峰. 离心泵启动过程瞬态流动的数值模拟和实验研究[D]. 杭州：浙江大学，2009. Li Zhifeng. Numerical Simulation and Experimental Study on the Transient Flow in Centrifugal Pump During Starting Period [D]. Hangzhou: Zhejiang University, 2009. (in Chinese with English abstract)

[5]李伟. 斜流泵启动过程瞬态非定常内流特性及实验研究[D]. 镇江：江苏大学，2012. Li Wei. Experimental Study and Numerical Simulation on Transient Characteristics of Mixed-flow Pump During Starting Period [D]. Zhenjiang: Jiangsu University, 2012. (in Chinese with English abstract)

[6]张玉良，朱祖超，崔宝玲，等. 离心泵停机过程非定常流动的数值模拟[J]. 工程热物理学报，2012，33(12)：2096－2099. Zhang Yuliang, Zhu Zuchao, Cui Baoling, et al. Numerical simulation of unsteady flow in centrifugal pump during stopping period[J]. Journal of Engineering Thermophysics, 2012, 33(12): 2096－2099. (in Chinese with English abstract)

[7]周大庆，刘跃飞. 基于VOF模型的轴流泵机组起动过程数值模拟[J]. 排灌机械工程学报，2016，34(4)：307－312. Zhou Daqing, Liu Yuefei. Numerical simulation of axial pump unit startup process using VOF model[J]. Journal of Drainage and Irrigation Machinery Engineering, 2016, 34(4): 307－312. (in Chinese with English abstract)

[8]周大庆，钟淋涓，郑源，等. 轴流泵装置模型断电飞逸过程三维湍流数值模拟[J]. 排灌机械工程学报，2012，30(4)：401－406. Zhou Daqing, Zhong Linjuan, Zheng Yuan, et al. Numerical simulation of transient flow in axial-flow pump unit model during runaway caused from power failure[J]. Journal of Drainage and Irrigation Machinery Engineering, 2012, 30(4): 401－406. (in Chinese with English abstract)

[9]金国栋，潘志军，孟金波，等. 斜式轴流泵装置模型的飞逸特性研究[J]. 水动力学研究与进展A辑，2013，28(5)：591－596. Jin Guodong, Pan Zhijun, Meng Jinbo, et al. Study of the runaway character of slanted axial-flow pump[J]. Chinese Journal of Hydrodynamics A, 2013, 28(5): 591－596. (in Chinese with English abstract)

[10]苟东明，郭鹏程，罗兴锜，等. 抽水蓄能电站泵工况断电飞逸过渡过程三维耦合数值研究[J]. 水动力学研究与进展A辑，2018，33(1)：28－39. Gou Dongming, Guo Pengcheng, Luo Xingqi, et al. 3-D combined simulation of power-off runaway transient process of pumped storage power station under pump condition[J]. Chinese Journal of Hydrodynamics A, 2018, 33(1): 28－39. (in Chinese with English abstract)

[11]张永学，侯虎灿，徐畅，等. 熵产方法在离心泵能耗评价中的应用[J]. 排灌机械工程学报，2017，35(4)：277－282. Zhang Yongxue, Hou Hucan, Xu Chang, et al. Application of entropy production method to centrifugal pump energy loss evaluation[J]. Journal of Drainage and Irrigation Machinery Engineering, 2017, 35(4): 277－282. (in Chinese with English abstract)

[12]王松岭，张磊，叶学民，等. 基于熵产理论的离心风机性能优化[J]. 中国电机工程学报，2011，31(11)：86－91. Wang Songling, Zhang Lei, Ye Xuemin, et al. Performance optimization of centrifugal fan based on entropy generation theory[J]. Proceedings of the CSEE, 2011, 31(11): 86－91. (in Chinese with English abstract)

[13]段璐，吴小林，姬忠礼. 熵产方法在旋风分离器内部能耗分析中的应用[J]. 化工学报，2014，65(2)：583－592. Duan Lu, Wu Xiaolin, Ji Zhongli. Application of entropy generation method for analyzing energy loss of cyclone separator[J]. CIESC Journal, 2014, 65(2): 583－592. (in Chinese with English abstract)

[14]Li Xiaojun, Jiang Zhiwu, Zhu Zuchao, et al. Entropy generation analysis for the cavitating head-drop characteristic of a centrifugal pump[J]. Proceeding of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2018, 232(24): 4637－4646.

[15]Li X, Zhu Z, Li Y, et al. Experimental and numerical investigations of head-flow curve instability of a single-stage centrifugal pump with volute casing[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2016, 230(7): 633－647.

[16]Pei J, Meng F, Li Y, et al. Effects of distance between impeller and guide vane on losses in a low head pump by entropy production analysis [J]. Advances in Mechanical Engineering, 2016, 8(11): 756466032.

[17]Gong R, Wang H, Chen L, et al. Application of entropy production theory to hydro-turbine hydraulic analysis[J]. Science China Technological Sciences, 2013, 56(7): 1636－1643.

[18]Li Deyou, Wang Hongjie, Qin Yonglin, et al. Entropy production analysis of hysteresis characteristic of a pump-turbine model[J]. Energy Conversion and Management, 2017, 149: 175－191.

[19]张亚太，杨宝锋，陈炜，等. 基于熵产理论的水翼空化特性研究[J]. 推进技术，2019，40(7)：1490－1497. Zhang Yatai, Yang Baofeng, Chen Wei, et al. Study on cavitation characteristics of hydrofoil based on entropy production theory[J]. Journal of Propulsion Technology, 2019, 40(7): 1490－1497. (in Chinese with English abstract)

[20]Yang Baofeng, Li Bin, Chen Hui, et al. Entropy production analysis for the clocking effect between inducer and impeller in a high-speed centrifugal pump[J]. Proceedings of the Institution of Mechanical Engineers, 2019, 233(15): 5302－5315.

[21]Chang Hao, Shi Weidong, Li Wei, et al. Energy loss analysis of novel self-priming pump based on the entropy production theory[J]. Journal of Thermal Science, 2019, 28(2): 306－318.

[22]Bejan A. Entropy Generation Minimization-The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes[M]. New York: CRC Press LLC, 1995: 47－57.

[23]Herwig H, Kock F. Direct and indirect methods of calculating entropy generation rates in turbulent convective heat transfer problems[J]. Heat and Mass Transfer, 2007, 43(3): 207－215.

[24]Kock F, Herwig H. Local entropy production in turbulent shear flows: A high-reynolds number model with wall functions [J]. International Journal of Heat and Mass Transfer, 2004, 47: 2205－2215.

[25]张翔，王洋，徐小敏，等. 低比转数离心泵叶轮内能量转换特性[J]. 农业机械学报，2011，42(7)：75－81. Zhang Xiang, Wang Yang, Xu Xiaomin, et al. Energy conversion characteristic within impeller of low specific speed centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(7): 75－81. (in Chinese with English abstract)

Transition process characteristics of centrifugal pump with power-off based on entropy production theory

Feng Jianjun1, Zhang Yu1, Zhu Guojun1※, Li Yunzhe2, Li Wenfeng2, Luo Xingqi1

(1.,’,’710048,; 2.,311121,)

In this paper, a transient numerical calculation method is established based on ANSYS CFX software and user-defined program, which can simulate the power-off runaway transient characteristics of a centrifugal pump. The variation rule of external characteristic parameters with time can be obtained through numerical calculations and compared with experimental data. The comparison of results show that the simulation results agree well with experimental results, the proposed numerical method has been therefore validated. During the power-off runaway transient process, the centrifugal pump system will successively undergo the pump condition, braking condition, turbine condition and runaway condition, with external characteristic varying significantly during the process. Internal flow structure is closely related to external characteristic and affects each other. The hydraulic loss due to friction and unstable flow patterns in the pump causes a drop in hydraulic efficiency. The traditional method for analyzing the hydraulic loss is by evaluating the total pressure drop, which has certain limitations and cannot determine the exact locations at which the high hydraulic loss occurs. In this study, entropy production theory has been adopted to obtain a detailed distribution of the hydraulic loss in the centrifugal pump. Through the use of the entropy production theory, the variation of the entropy production was obtained. The distribution of energy loss of flow components during this process is obtained by using the entropy generation theory, and the energy loss is analyzed. The results show that there is a clear correlation between the entropy production and the external characteristics of the centrifugal pump during the entire runaway process. The entropy production also undergoes dramatic changes at the moment of sudden changes in flow rate, rotational speed and torque. The main losses of the impeller, guide vanes and suction pipe are caused by turbulent dissipation, and the wall entropy production accounts for about 10%–15% of this total entropy production, which means the wall effect could not be ignored. However, the loss of the volute is mainly due to the strong wall effect in the near wall region, which is different from other three flow components, denoting the main loss generation mechanism is different. In addition, it is found that both the energy loss and variation range of the impeller and guide vanes are relatively larger than those of other flow components in the whole process. By analyzing the distribution of the local entropy production of the impeller and the vanes at different stages, it is intuitively obtained from the energy point of view that the high loss region of the internal flow field is the largest in the braking condition, and the high loss area fills the entire impeller flow path when the rotational speed drops to 0. The results obtained in this paper can improve the understanding of transient characteristics of a centrifugal pump during the power-off transient condition.

centrifugal pump; flow field; numerical simulation; power-off runaway; entropy production; transient characteristics; energy loss

冯建军，张 钰，朱国俊，李昀哲，李文锋，罗兴锜. 采用熵产理论的离心泵断电过渡过程特性[J]. 农业工程学报，2020，36(4)：10－17. doi：10.11975/j.issn.1002-6819.2020.04.002 http://www.tcsae.org

Feng Jianjun, Zhang Yu, Zhu Guojun, Li Yunzhe, Li Wenfeng, Luo Xingqi. Transition process characteristics of centrifugal pump with power-off based on entropy production theory[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(4): 10－17. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.04.002 http://www.tcsae.org

2019-11-14

2020-01-11

国家重点研发计划资助（2018YFB1501900）；国家自然科学基金（51679195）；陕西省自然科学基础研究计划资助项目（2019JQ-044）；陕西省教育厅科研计划项目（19JK0570）

冯建军，教授，研究方向为流体机械流动理论与优化设计、流体机械振动与稳定性分析。Email：jianjunfeng@xaut.edu.cn

朱国俊，讲师，研究方向为流体机械流动理论与优化设计、流动分析等。Email：guojunzhu@xaut.edu.cn

10.11975/j.issn.1002-6819.2020.04.002

TK733+.3

A

1002-6819(2020)-04-0010-08