一种个性化k近邻的离群点检测算法
2020-04-10樊瑞宣姜高霞王文剑
樊瑞宣,姜高霞,王文剑
1(山西大学 计算机与信息技术学院,太原 030006)2(山西大学 计算智能与中文信息处理教育部重点实验室,太原 030006)
1 引 言
在实际应用中,由于数据来源和构成的多样性,使得存在这样一类数据点,它们与大部分数据的一般行为或者模型不一致,这样的数据对象称为离群点.对于离群点的定义,目前最广为人接受的是Hawkins[1]给出的描述:“离群点是在数据集中偏离大部分数据的数据,使人怀疑这些数据的偏离并非由随机因数产生,而是产生于完全不同的机制”.离群点检测是数据挖掘的一个重要分支,被广泛应用在各种领域,如欺诈检测[2,3]、图像检测[4,5]、医学分析[6-8]、信号异常检测[9]等.离群点可能包含潜在的信息,而这些信息对于识别系统中的异常行为具有重要的作用.
离群点检测的目的是要找出数据集中与其他数据相比显著异常的数据对象,然后帮助我们更好地理解和处理数据.现有的离群点检测算法大致可以分为基于统计、基于距离、基于密度及基于聚类等四类方法.
基于统计(又称为基于模型)的方法,其思想来源于统计学.先对数据集的分布作出假设,然后建立数据集的统计模型,根据模型采用不一致检验识别离群点[10].当数据的分布符合前提假设时,效果是非常好的.但是,对于实际的数据集来讲,我们并不知道它的分布是怎样的,而且一般来讲,也很难用标准的数据模型去拟合它,所以这类方法的离群点检测效果无法保证,因此,这类方法应用不多.
基于距离的方法是该领域内应用最多的算法,在不同的场景中,选取合适的距离度量方式(欧氏距离、马氏距离等),作为离群的判断准则,其中使用最为广泛的算法是k近邻(k-Nearest Neighbor,KNN)[11]方法.在此基础上,反向k近邻(Reversek-Nearest Neighbor,RKNN)[12]的方法被提出.目前有很多离群点检测算法都是基于KNN或者RKNN,如文献[13]提出的LDOF(Local Distance-based Outlier Factor)算法,该算法把点的k近邻平均距离与该点的k近邻内部平均距离之比作为该点的局部距离离群因子,以此判别数据对象是否为离群点.基于近邻的离群点检测算法与统计方法相比,计算比较简单,减少了在统计学方法中需要进行的学习模型和选择不一致检验相关的过多的计算,而且此类算法都是依据周围有限的近邻样本而不需要与整个的数据点进行判断,所以近邻方法被广泛运用在各种算法中.
基于密度的方法主要针对局部离群点检测,由于数据集的分布并非总是均匀的,所以会产生局部离群点.最具代表性的算法是Breunig等提出的局部离群因子(Local Outlier Factor,LOF)算法[14].该算法把点的密度与其邻域的平均密度比值作为局部离群因子,离群因子的值越大,代表该点的离群程度越高.这类方法假定非离群点对象周围的密度与其邻域周围的密度相似;而离群点对象周围的密度显著不同于其邻域周围的密度.在LOF算法的基础上,Jin等人又提出了INFLO(INFLuenced Outlierness)算法[15],该算法在计算离群因子时,不但考虑了k近邻,还同时考虑了反向k近邻对于该数据点的影响,此方法计算出的离群因子比LOF包含了更多的信息.
基于聚类的方法是通过观察数据对象和簇之间的关系,来寻找离群点.直观地,离群点是一个对象,它属于规模小的偏远簇,或者不属于任何一个簇.基于聚类的方法对无标签数据的离群点检测有效,另外,簇可以看做数据的概括,在得到簇以后,只需把检测对象和簇进行比较,就可以确定该数据对象是否是离群点.这个过程通常比较快,因为簇的个数通常远小于数据点的总数.目前已经出现了很多代表性算法,如DBSCAN[16],CLARANS[17],CHAMELEON[18],BIRCH[19]和CURE[20],但是这类算法在聚类过程中存在较多参数,而离群检测非常依赖于聚类结果,只有在聚类结果好的情况下,才能保证离群点检测效果.
在基于距离和基于密度的算法中,经常需要使用k近邻概念,因此,近邻参数k的选取无法避免,而k值的大小将会直接影响到算法的实际性能和检测效果.一般情况下,近邻参数k是人为设定的,为了设置合理的参数值,需要对数据集有一定的了解,并具有一定的先验知识.但是在实际操作中,这些先验知识往往很难得到.即使是对不同的数据集采用相同的算法,由于不同的数据集具有不同的特征,所以在设定k值时也没有太大的借鉴意义.
针对近邻参数k的敏感问题,基于不稳定因子的健壮离群点检测算法(Robust Outlier Detection Using the Instability Factor,INS)[21]被提出.INS算法首先是要找到每个点的邻居,确定邻域重心,然后不断扩大被检测点的邻域,根据邻域重心的位置变化确定每个点的不稳定因子,以此判断该点的离群程度.INS算法对近邻参数具有鲁棒性,但是该算法容易将处于稀疏区域与稠密区域交界处的正常点误判为离群点.文献[22]提出了自然邻居(Natural Neighbor,NaN)算法,通过这个算法可以计算得出自然邻居特征值(Natural Neighbor Eigenvalue,NaNE),然后将NaNE作为数据集中所有点的近邻参数,为k的自适应选择提供了新的思路.NaN算法虽然给出了一种不需要人为设定近邻参数k的方式,但依然对所有的数据点采用相同的k值,会让原本处于稀疏区域的数据点,由于近邻参数过大而增加计算时间.
本文提出一种个性化k近邻(PKNN)的离群点检测算法,数据集中的每个数据点可以采用不同的近邻数,而这个近邻数是通过算法自动确定的,不但可以避免人为设定参数问题,而且可以反应出数据集本身的分布特征,同时保留KNN的优势.
2 个性化k近邻的离群点检测方法
在现有的基于近邻的离群点检测算法中,都是由用户根据经验为数据集中的所有点统一设定一个k值,k值是否合适一般要经过实验验证.另外,由于数据分布不同,对于一个数据来说,采用相同的k值,可能会把离这个数据较远的点作为k近邻考虑,实际上对该点影响较小;也有可能会把离这个数据较近的近邻没有作为k近邻考虑,实际上对该点影响较大,所以检测效果不能保证.图1是传统KNN与PKNN中近邻分布示意图,p和q分别表示两个三角形点.对于传统KNN方法(如图1(a)所示),假设采取固定近邻数k=5,即p和q的近邻数Num(p)=Num(q)=5,两个圆圈分别表示p和q的5近邻.对于q来说,k取5符合q的分布特征,但是对点p本身的分布而言,k取5并不适合,会因为把较远的邻居考虑进来,降低计算效率,而且可能会干扰检测结果.而PKNN对每个数据点可以采用不同的近邻数.图1(b)中,点p和点q的近邻数并不相同,Num(p)=2,Num(q)=5.从分布来看,这个近邻参数更能体现出数据本身的特征:处于稠密区域的点具有更多的邻居,而处于稀疏区域的点具有更少的邻居.

图1 KNN与PKNN近邻分布示意图Fig.1 Distribution of nearest neighbors in KNN and PKNN
2.1 确定个性化近邻参数
在PKNN算法中,数据集中每个点都有一个自己专属的近邻个数,且这个近邻个数是由算法自动确定,不需要人为指定.
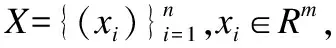
(1)
令Sk(xi)表示xi的k近邻集合,PK(xi)表示xi的个性化近邻集合,即
PK(xi)={xj│xj∈Sk(xi)且xi∈Sk(xj) }
(2)
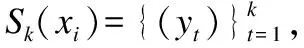
在个性化近邻参数计算结束后,会存在极少数点的近邻参数为0,这些点一般是孤立点,因此直接将其作为离群点.
本文确定近邻参数的方法与自然邻居(NaN)方法过程相同,但输出结果不同.NaN算法在迭代结束时输出最大k值,并且将它作为所有点的近邻参数,而PKNN则在迭代计算近邻过程中,记录并输出每个点的个性化k值.
2.2 计算离群度
得到每个点的个性化近邻参数以后,就可以判断每个点与其他点的不一致性,这里用离群度来度量这种不一致性.令D(xi)表示xi的原始k近邻平均距离,即
(3)
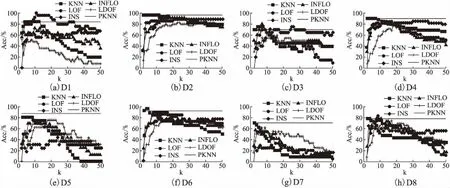
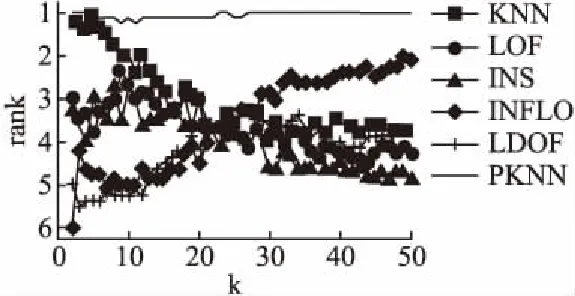
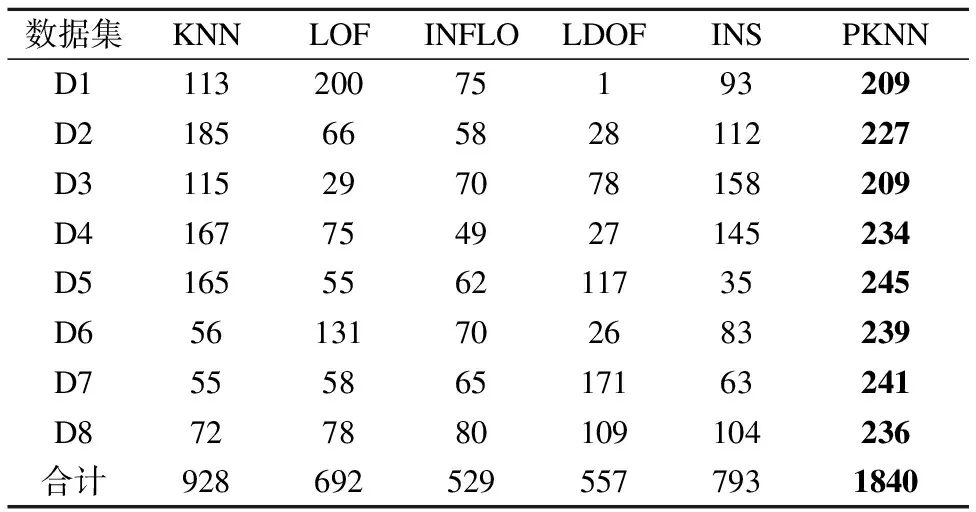
传统KNN采用原始k近邻平均距离D(xi)作为离群判别准则,D(xi)越大,xi的离群程度越高.在PKNN算法中,若采用D(xi)作为离群判别准则,由于每个点的近邻个数不同,有可能会导致稀疏区域的点的近邻平均距离小于稠密区域的点的近邻平均距离,即稠密区域的点容易被判别为离群点.图2是一个简单的例子,图中p和q分别表示两个三角形点,Num(p)=1,Num(q)=3,圆圈分别表示p和q的近邻范围,图中数值表示每个点的近邻距离.由图2可以看出:D(p)=1,D(q)=1.5,故D(p) (4) 图2 近邻平均距离示意图Fig.2 Mean distance of nearest neighbors 对于图2中的例子,使用修正后的离群准则,可得出D′(p)>D′(q),表明p的离群程度更大,因此,与数据的实际分布相符.PKNN算法中,Num(xi)=0的点在第一阶段已被判别为离群点,所以不会出现D′(xi)不可计算的情况. PKNN算法的主要步骤总结如下: 算法1.PKNN算法 输出:Top-n离群点 Step1.初始化搜索轮数k=1;∀xi∈X,PK(xi)=Ø,Num(xi)=0. Step2.∀xi∈X,重复执行以下步骤: Step 2.2.计算cnt,并使用变量rep保存cnt保持不变的次数. Step3.得到离群点集合M={xi│Num(xi)=0,i=1,2,…,n},若‖M‖≥Top-n,则顺序取M中前Top-n个点作为离群点,算法结束,否则进行下一步骤. Step4.∀xi∈X-M,计算离群度D′(xi). Step5.选取D′(xi)中值最大的Top-n-‖M‖个数据点,并与M中的点一起作为Top-n离群点. Step6.算法结束. 本算法主要分为确定个性化近邻个数和计算离群度两个阶段.其中,Step 2的循环部分是自适应确定每个点的近邻数的过程,Step 3是在近邻数为0的点中选取一定数量的点作为离群点,Step 4和Step 5是对其余点计算离群度,然后确定离群点.第一阶段的时间复杂度为O(n2),第二阶段的时间复杂度为O(n),因此,本算法的时间复杂度为O(n2). 为了进一步说明PKNN算法的计算过程,本节给出一个示例.图3是含有16个样本的原始分布,其中编号为8和16的是离群点,样本信息及实验结果如表1所示. 图3 示例数据分布Fig.3 Distribution of samples 方法首先确定每个样本的个性化近邻数.在本示例中,根据算法1可得实验在第6轮搜索结束后,即可满足终止条件,循环停止,选取编号为3、8、16的样本来说明自适应确定近邻数以及计算离群度的过程. 1)对于样本3,根据公式(2),寻找个性化近邻的迭代过程如下: k=1时:PK1(3)={5},Num1(3)=1. k=2时:PK2(3)={6},Num2(3)=1. k=3时:PK3(3)={1},Num3(3)=1. k=4时:PK4(3)=Ø,Num4(3)=0. k=5时:PK5(3)={2,7},Num5(3)=2. k=6时:PK6(3)={4},Num6(3)=1. 迭代结束,可得:PK(3)={5,6,1,2,7,4},Num(3)=6,根据公式(4)计算样本3的离群度:D′(3)=2.41. 2)对于样本8,根据公式(2),寻找个性化近邻的迭代过程如下: k=1时:PK1(8)=Ø,Num1(8)=0. k=2时:PK2(8)=Ø,Num2(8)=0. k=3时:PK3(8)=Ø,Num3(8)=0. k=4时:PK4(8)={9},Num4(8)=1. k=5时:PK5(8)=Ø,Num5(8)=0. k=6时:PK6(8)={10},Num6(8)=1. 迭代结束,可得:PK(8)={9,10},Num(8)=2,根据公式(4)计算样本8的离群度:D′(8)=3.65. 3)对于样本16,根据公式(2),寻找个性化近邻的迭代过程如下: k=1时:PK1(16)=Ø,Num1(16)=0. k=2时:PK2(16)=Ø,Num2(16)=0. k=3时:PK3(16)=Ø,Num3(16)=0. k=4时:PK4(16)=Ø,Num4(16)=0. k=5时:PK5(16)=Ø,Num5(16)=0. k=6时:PK6(16)=Ø,Num6(16)=0. 迭代结束,可得:PK(16)=Ø,Num(16)=0,由于样本16的个性化近邻数为0,直接被作为离群点. 表1 示例数据信息及其实验结果Table 1 Samples and experimental results 在本例中,离群点个数为2.由表1可知,个性化近邻数为0的只有样本16,已经被作为离群点.计算并比较其他15个样本的离群度,可得样本8的离群度最大,因此样本8也是离群点.PKNN算法最终得到的离群点是样本16和样本8,与数据集中的真实离群点保持一致. 为了验证所提出的算法的有效性,本文在人工数据集上进行了仿真实验,数据集的说明如表2所示. 8组数据集的分布如图4所示,其中圆形点代表正常数据点,三角形点是离群点. 表2 实验数据集Table 2 Experimental data sets PKNN与NaN算法的近邻参数k均为自动确定,实验首先将PKNN算法得到的个性化近邻参数与NaN算法的NaNE进行比较.然后选取五种代表性离群点检测算法(KNN、LOF、INFLO、LDOF、INS)与PKNN进行离群点检测效果对比.评价指标采用离群点检测准确率,即: Acc=(a/b)×100% (5) 其中,a是检测出的真实离群点的数量,b是离群点的数量. 图4 数据集分布Fig.4 Distribution of data set 3.2.1 近邻参数k的比较 实验首先确定不同点的个性化k值.PKNN算法在8个数据集上得出的k值分布如图5所示,其中,横轴表示k值大小,纵轴表示在近邻个数等于k值时对应的数据点个数占整个数据集的比例.当k取最大值时,即为NaNE. 从图5可以看出,数据点的k值主要分布在后半部分,且随着k值的增大,近邻为k的数据点所占的比例呈上升趋势.说明大部分数据点都分布在稠密区域,且这些点的近邻个数在迭代过程中不断增加,与本文所使用的数据集的分布一致.PKNN在8个数据集上取NaNE的点的个数占整个数据集的比例,除了D5是43.11%,其他数据集上均小于40%.在NaN算法中,对所有数据点均采用NaNE作为近邻参数.从图中可以看出,存在一些近邻个数很小甚至为0的数据点,对于这些点,如果采用NaNE作为近邻参数,可能会将一些类别模式不同的点作为邻居,影响检测结果,同时因为考虑了更多的近邻而降低了计算效率. 图5 k值分布Fig.5 Distribution of k values 3.2.2 离群点检测准确率的比较 由于对比算法的检测结果均依赖于参数k的设置,所以实验中比较了不同k值下的检测准确率,如图6所示.图中横轴表示近邻参数k值,纵轴表示准确率.横线表示PKNN计算出的准确率(这里每个点的k值不完全相同,所以只给出准确率,与k的变化无关). 图6 不同检测算法在取不同k值时的准确率Fig.6 Accuracies of different detection methods over a range of k values 从图6中可以看出,在个别数据集(D1,D3,D6,D8)上,其他算法仅在少数特定的k值下的准确率超过PKNN,从整体来讲,其他算法的准确率由于受到近邻参数k的影响,上下波动范围较大,在大部分k值下的准确率均小于PKNN算法准确率.对于比较算法,LOF在D1上的准确率相对较高,说明LOF对于D1这种分布密度明显不同的数据集具有较好的检测效果;INS在近邻参数不断变大的过程中,准确率变化不明显,表现了INS对近邻参数的鲁棒性;其他算法检测效果受近邻参数影响较大. 为了更加直观地比较不同算法的优劣,图7给出了PKNN算法和其他算法在不同k值下的准确率比较结果排名,其中横轴表示近邻参数k值,纵轴表示排名.PKNN算法中每个点的k值是唯一确定的,且不完全相同,所以图7只给出PKNN的准确率排名,与k的变化无关. 图7 不同算法准确率排名Fig.7 Accuracies ranking of methods 从图6可知,PKNN算法在每个数据集上的准确率是不变的,而其他算法均受参数k的影响,所以准确率是变化的,会在极少数特定的k值下的准确率超过PKNN,导致图7中PKNN算法的排名出现了微小的波动,尽管如此,其排名始终最高,而其他对比算法的排名波动较大. 表3 不同算法准确率高于其他算法的次数Table 3 Number of wins in accuracy 表3给出了每种算法的准确率高于其他算法的次数比较(结果相同的次数不包括在内),对于每一个数据集,表中数值为每种算法k从2到50上的次数累加结果. 从表3可以看出,PKNN算法在8组数据集上准确率高于其他算法的次数均为最高,且总次数远高于其他算法,表现出PKNN在不同数据集上具有很好的自适应性.对于其他方法,在不同数据集上表现不同,整体来看,KNN在3个数据集(D2,D4,D5)上较好,LOF和LDOF分别在2个数据集(D1,D6;D7,D8)上较好,INS在数据集D3上较好,INFLO表现最差. 以上实验结果表明,PKNN算法在面对不同的数据集时,可以根据数据集本身的特征自动确定每个点的近邻参数,相比于其他算法来说,不但避免了参数选择的问题,还可以达到很高的准确率,算法的结果与人工情况下对数据的基本判断相符合. 近邻思想被广泛应用在离群点检测方法中,而近邻参数k的取值对检测结果会产生很大影响.现有的方法大多都是人为设定参数k,且所有点都采用相同的k值.为了避免k的选择问题,本文提出了PKNN算法,在不需要提前指定近邻参数k的情况下,可以根据数据集自身的分布,自适应地选择近邻并确定每个点的k值,然后去寻找离群点.PKNN不但避免了参数k的选择问题,与其他较为主流的离群点检测算法相比,也具有更好的检测效果和性能.然而由于PKNN需要对每个点寻找近邻,所以时间复杂度相对较高,如何提高其效率值得进一步研究.
2.3 PKNN算法

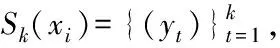
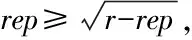
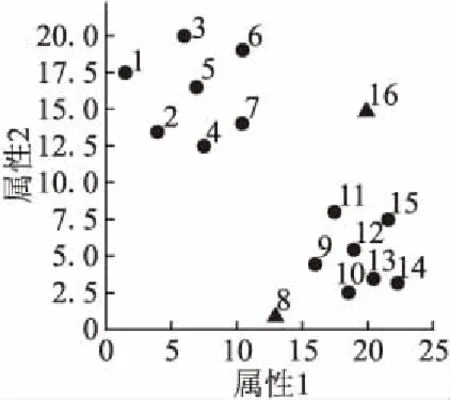
2.4 PKNN算法示例

3 实验及结果分析
3.1 实验设计
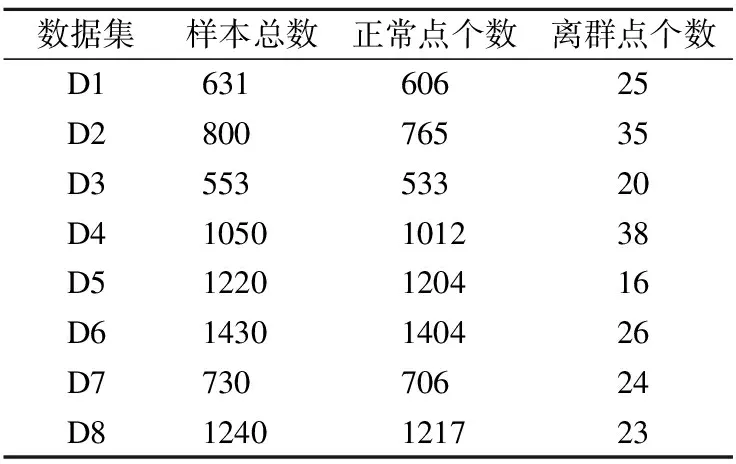
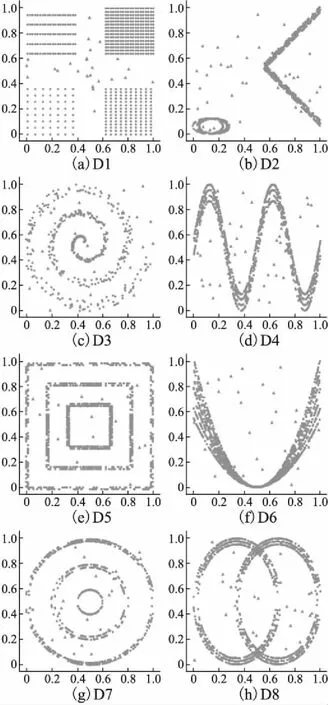
3.2 实验结果与分析
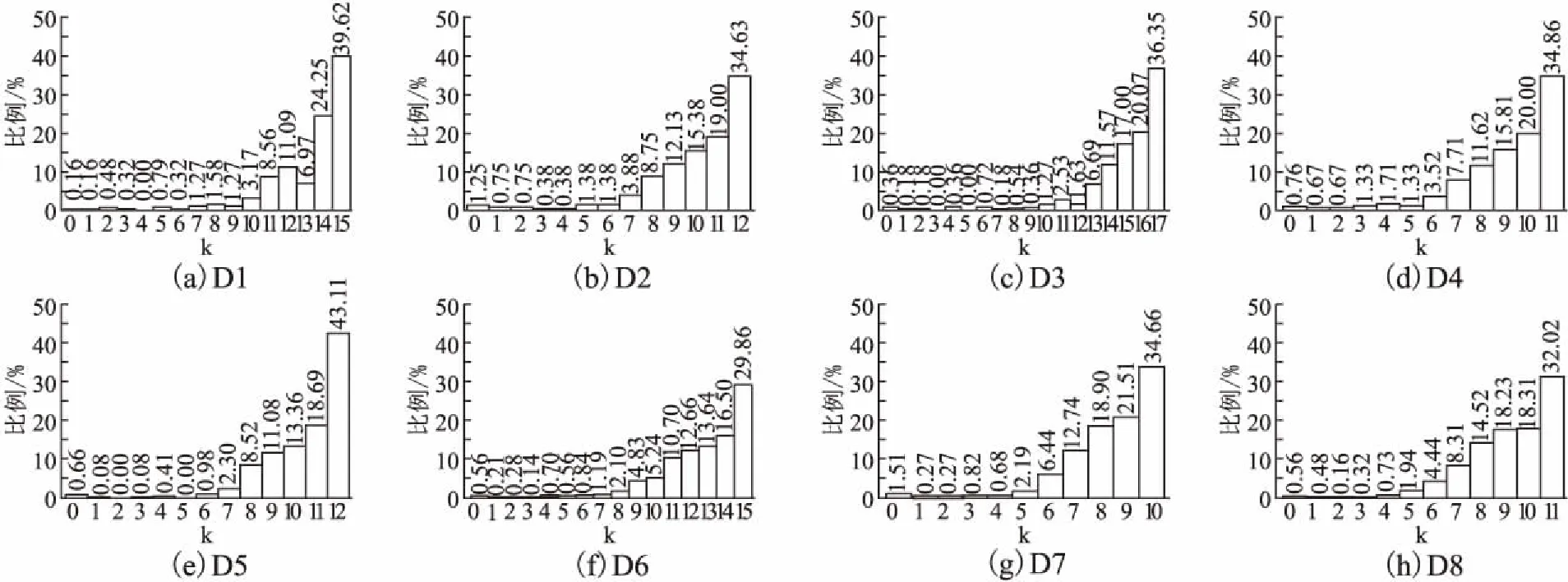
4 结 论
