基于因子分析模型的噪声稳健脑电信号分类方法

彭锦强

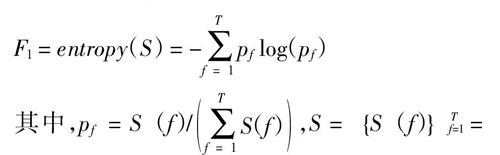
摘   要：脑电信号的非线性、非平稳性和微弱性造成对运动想象脑电信号的分类存在特征提取困难，分类结果不理想，分类性能受噪声影响明显等问题。为此，提出了一种基于因子分析（Factor Analysis，FA）模型的噪声稳健运动脑电信号分类方法。首先利用FA模型對脑电信号中存在的噪声分量进行抑制，针对重构信号可分性较差的问题，将其转换至功率谱域，进而提取三维能够反映不同运动状态的功率谱特征，最后利用支撑向量机（Support Vector Machine，SVM）分类器对所提特征向量进行分类判决。基于Graz数据的验证实验表明，所提方法可以明显提升低信噪比条件下的分类性能，在实际工程应用中具备较强的推广泛化

能力。

关键词：脑电信号分类;因子分析模型;特征提取;噪声稳健;

中图分类号：TP39                                             文献标识码：A

Noise Robust EEG Signal Classification Method Based

on Factor Analysis Model

PENG Jin-qiang？覮

（Huizhou City Vocational College，Huizhou，Guangdong 516025，China）

Abstract：In view of the difficulty of feature extraction and the obvious influence of noise on the classification of motor EEG signals，this paper presents a noise robust EEG signal classification method based on factor analysis（FA） model. Firstly，FA was utilized to suppress the noise components in EEG signals，and then the original signals with poor separability were converted to the power spectrum domain and the three-dimensional power spectrum features with good separability were extracted. Finally，Support Vector Machine（SVM） classifier was used to classify the feature vectors. The verification experiment with Graz data shows that the proposed method can significantly improve the classification performance under the condition of low SNR，and has a strong generalization ability.

Key words：classification of EEG signals;factor analysis model;feature extraction;noise robust;

1973年Vidal为了帮助运动障碍患者实现与外界的信息交互，第一次提出了脑-机接口（Brain Computer Interface，BCI）技术[1-2]。BCI技术是在大脑与计算机或外部通信设备之间直接建立联系，而不依靠传统的脑外周神经和肌肉系统等传统大脑输出通路，其实现途径是利用计算机或其它外围设备对特定任务下的脑电信号（Electro Encephalogram Gram，EEG）进行采集，进而运用模式识别算法对数据进行分析并将其与特定任务（例如抬左手）建立联系，从而达到向外界传输信息的目的。模式识别作为BCI中的关键技术也成为了当前研究的难点和热点[3]。

典型的模式识别算法包含训练和测试两个阶段[4-5]，通常训练阶段可以离线完成，测试阶段需要在线对测试样本实现快速判决。训练阶段和测试阶段的数据处理流程又分为预处理，特征提取/特征选择和分类识别，其中预处理是指对信号中包含的噪声等对特征提取和分类识别无用的信息进行剔除，增强有用信息的过程;特征提取是指从信号中提取一些反映不同目标差异特性的特征替代高维原始信号，达到降低运算量的目的;特征选择是指从特征提取阶段获得的特征中选择对分类识别性能影响较大的特征，进一步降低分类识别阶段的运算时间，需要指出的是特征选择并不是模式识别中必须的步骤;分类识别分为训练阶段的分类器设计和测试阶段的分类决策，其中分类器设计是指在训练阶段对分类器进行选择并利用训练阶段提取的特征对分类器参数进行寻优，测试阶段的分类决策是利用训练好的分类器对测试样本的类别属性进行判决。

目前国内外针对运动脑电信号的分类识别开展了大量的研究，并取得了显著的进展。例如文献[6]利用短时傅里叶变换将原始脑电信号转换至时频域，提取能量熵特征并利用SVM分类器对特征进行分类识别;文献[7，8]将小波变换引入脑电信号分类领域，对原始信号进行小波分解并提取特征，最后利用线性分类器进行分类识别得到较好的分类结果;文献[9]利用改进的经验模态分解算法对脑电信号进行分析，将原始信号自适应的分解为一系列本征模函数，并提取能量特征和平均幅度差特征构建特征向量，最后利用SVM[10]分类器进行分类识别，得到了88.6%的正确识别率。结合图1可以看出，上述研究都是集中在对模式识别算法中的特征提取和分类识别两个方面，而脑电信号除了非线性、非平稳性外，微弱性是其另一个显著特点，脑电信号幅度通常处于5 uV ～ 300 uV之间，而外界干扰信号和噪声电压通常处于mV级，导致脑电信号容易受到噪声污染，也是当前分类方法在低信噪比情况下的分类性能下降的主要原因[11]。因此，在对运动脑电信号进行特征提取前，需要对其中包含的噪声分量进行抑制。

提出了一种基于因子分析模型[10]的噪声稳健运动脑电信号分类方法，首先利用因子分析模型对脑电信号中包含的噪声分量进行抑制，在此基础上提取三维特征将可分性较差的原始信号转换至特征域，最后利用SVM分类器对所提特征进行分类识别，基于实测数据的实验结果表明所提方法可以获得较好的分类性能，并且在低信噪比条件下具有较强的鲁棒性。

1   实验数据介绍

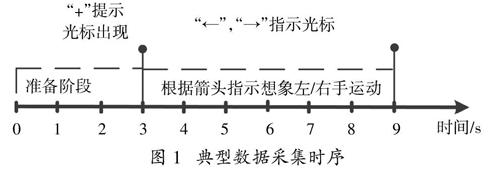
实验采用奥地利格拉兹技术大学（Graz University of Technology）提供的脑机接口数据[12]，采用了其中Data ⅢA数据集中的K3b、K6b和L1b三组运动脑电数据。该数据通过符合国际标准的64组EEG放大器采集获得，参考电极设置为左侧乳突位置。一组典型数据的采集流程如图1所示：

■

图1   典型数据采集时序

1）时间：[0 s ～ 2 s];显示屏：黑屏;受试者：放松状态;

2）时间：2 s;显示屏：亮起并出现“+”光标;受试者：准备开始实验;

3）时间：[3 s ～ 9 s];显示屏：出现“←”或“→”箭头;受试者：根据光标提示对应想象左手或者右手运动。

整个数据集中包含C3和C4两个通道的数据共280组，其中训练数据和测试数据各一半为140组，包含70组想象左手运动实验数据，70组想象右手運动实验数据。实验数据的采集采用128 Hz的采样频率，每组数据采集时间为9 s，包含1152个采样点。由于每次实验从第3 s开始，本文实验只对第3 s到第9 s之间的768个样本点进行分析。

2   预处理

2.1   因子分析模型

因子分析模型（Factor Analysis，FA）是一种广泛应用于数据降维及概率分布描述的概率隐空间模型，FA将观测数据映射到一组基函数张成的子空间，并利用隐变量表征数据在隐空间的分布特性。相对于其它统计模型，FA模型具备特有的优点：1） 模型的自由度小，不会引起“维数灾难”;2） 考虑了数据中的相关性，对数据结构描述准确;3） 具备稀疏性，能够用较少的隐变量实现对原始信号空间的描述。因子分析模型可以表示为：y = Dx + u + ε，其中D = [d1，d2，…，dK]∈RL×K 为因子加载矩阵， u为观测信号的均值，ε为高斯白噪声。传统FA模型的因子个数K需要预先设定，但是因子个数设置过大会造成过匹配，设置过小则不能充分描述数据的统计分布。本文采用贝叶斯框架下的FA模型，利用Beta-Benoulli先验自动确定因子个数 ，此时模型结构可以表示为：

yn = D（zn·xn） + εnznk = Bernoulli（πk）πk = Beta（a0/K，b0（K - 1）/K），k =1，…，Kεn = N（0，γ-1I）γ = Gamma（c0，d0） （1）

对于上式给出的概率模型，本文采用变分贝叶斯期望最大（Variational Bayes Expectation Maximization ，VBEM）算法求解，这种算法基于变分推理，通过迭代寻找最小化KL（Kullback-Leibler）距离的边缘分布来近似联合分布。根据VBEM算法，参照文献[10]可以推导出每个参数的更新公式为：

1.更新q（z）分布：

〈L（Z，Θ）〉 q（Π）q（γ）  = 〈γ〉■■zkwnk■+

■[zk〈Inπk〉+（1-zk）〈In（1-πk）〉]+const

（2）

其中wnk = znk·xn，根据式（2）可以推断q（z）具有如下形式：

q（z） = ■q（zk）

= ■Bernoulli（■）  （3）

上式中，zk = 1和zk = 0的概率由下式决定：

p（zk = 1）∝exp（〈Inπk〉） × exp（〈γ〉■||wnk||2）

p（zk = 0）∝exp（〈In（1 - πk）〉）               （4）

根据上述结果可以得到zk的后验期望为：

〈zk〉=■

（5）

2.更新 分布

■

+ const                       （6）

根据上式可知q（π）具有如下形式：

q（πk） = ■q（πk） = ■Beta（πk|■k，■k）     （7）

3.更新

〈L（Z，Θ）〉 q（z）q（π） =

DNln（γ） - γ■ +

（c0-1）lnγ+const          （8）

在上述分析的基础上，可以求得γ的后验期望为：

〈γ〉 = ■     （9）

4.终止条件：

当连续两次迭代结果的变化小于预先设置的门限时，迭代终止，此时得到的x即为噪声抑制后的信号。由于所提模型对超参数的初值不敏感，因此在接下来的实验中，将模型中超参数初值设置为 a0 = b0 = 1，c0 = d0 = 10-6，即超参数不携带任何信息。而因子个数K的初值可以设置为任意大于1的整数，本文设置K = 20，同时将终止门限为设置为10-8。

2.2   仿真验证

为了验证所提方法的噪声抑制性能，利用仿真产生测试信号x（t）：

x（t） = s（t） + n（t）

= cos（2πf1t）+cos（2πf2t）+cos（2πf3t）+n（t）

（10）

其中s（t）为不含噪声信号，由三个频率分别为f1 = 1 100 Hz，以及f2 = 700 Hz的点频信号组成的周期信号，n（t）表示零均值高斯白噪声，噪声功率根据不同信噪比（Signal Noise Ratio，SNR）计算得到，本文中SNR定义如下：

SNR=10×long10■=10×long10■    （11）

上式中，■为表示不含噪信号s（t）的平均功率，P s（t） = s（t）■代表s（t）中第t个样本的功率，Pn为噪声n（t）的平均功率，D为仿真信号长度。

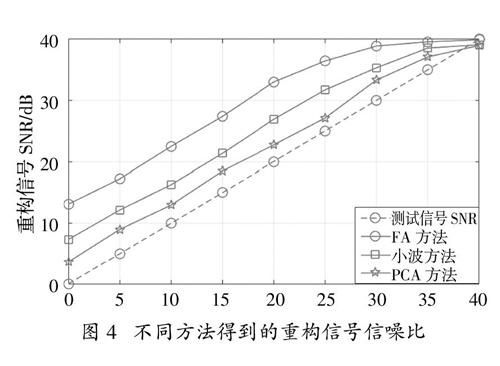
图2（a）、图2（b）和图2（c）分别给出了仿真得到的不含噪信号s（t），SNR=0 dB时的测试信号x0 dB（t）以及SNR = 10 dB时的测试信号x10 dB（t）。可以看出随着SNR的下降，s（t）的周期性越来越不明显，表明信号中的有用信息被无序的噪声污染，因此在对信号进行特征提取前需要事先进行噪声抑制预处理。图3给出了利用所提方法、传统小波去噪方法以及主成分分析方法（Principal Component Analysis，PCA）对x0 dB（t）进行噪声抑制得到的结果，其中PCA方法选用能量占特征向量95%的大特征值个数作为主分量个数。图4给出了对不同SNR测试信号进行噪声抑制得到的重构信号的SNR水平。从上述结果可以看出，利用所提因子分析模型在不同SNR情况下均可以获得最好的噪声抑制性能。

■

图4   不同方法得到的重构信号信噪比

3   特征提取和分类识别

3.1   特征提取

在得到噪声抑制的重构信号后，最直接的方式是将重构信号直接作为特征向量进行分类，但是由于重构信号维度往往较高，直接进行分类存在计算量大的问题，同时重构信号中除了对分类有益的信息之外不可避免的会存在一些冗余信息，因此需要采用特征提取的方式将重构信号转换至特征域，在降低运算量的同时剔除信号中的冗余信息，提升分类识别性能。

特征1：重构信号功率谱的熵：

F1 = entropy（S） = -■pf log（pf）

其中，pf  = S（f）/■S（f），S = {S（f）}T   f=1= FFT（■）■为重构信号■的功率谱。功率谱的熵特征描述的是信号的能量分布特性，信号的能量分布越集中，则对应的熵越小。

特征2：重构信号功率谱的二阶中心距：

F2 = ■（f - f）2 pf

其中，f = ■f × pf 二阶中心距特征反映了信号相对于其质心的分布情况。

特征3：重构信号功率谱的方差：

F3 = ■■S（f） - ■■S（f）

方差特征反映的是信号的波动特性。

图5给出了对第2部分介绍的脑电信号实测数据提取上述三维特征得到的二维归一化特征分布图，其中“o”表示对想象左手运动EEG信号提取的特征值，“+”表示对想象右手运动EEG信号提取的特征值，从图5可以看出，在特征域，想象两种运动产生的EEG信号具有较好的可分性。

图6给出了对脑电信号实测数据按式（15）增加高斯白噪声得到SNR=10 dB的含噪信号后，同样提取上述三维特征得到的二维归一化特征分布图，图7给出了利用所提因子分析模型对SNR=10dB含噪信号进行噪声抑制得到重构信号后，再次提取特征得到的特征分布图。对比图5，图6和图7可以看出，对SNR=10 dB含噪信号提取的特征在特征空间中的可分性相对于不含噪信号特征明显降低，而经过所提因子分析模型进行噪声抑制后得到重构信号的二维特征分布的可分性接近于原始不含噪信號，因此在特征提取前需要提前对信号中的噪声分量进行抑制。

图5   特征值分布图

图6   特征值分布图，SNR=10 dB含噪信号

图7   因子分析模型重构信号特征值分布图

3.2   分类识别

在分类识别阶段，需要选取合适的分类器实现对特征提取阶段获得的特征进行分类判决，当前应用比较广泛的分类器有线性分类器、神经网络分类器和支撑向量机等，其中SVM在解决小样本，非线性及高维模式分类问题中表现出许多特有的优势，因此本文选用SVM分类器对运动脑电信号进行分类。

实验中SVM选用高斯核，采取交叉验证的方式选择高斯核函数，首先将训练样本分为4组，每次实验中从其中选取一组作为训练集另外三组作为测试集对核参数在[0，5]范围，步长为0.1进行寻优，最终选取分类性能最好的核参数（1.4）作为最优参数对测试数据进行分类决策。

图8给出了不同信噪比条件下所提方法和其它文献中介绍方法的分类结果，其中文献[13]采用小波包能量进行特征提取，并利用基于马氏距离的线性分类器对所提特征进行分类，文献[14]在文献[13]的基础上对 C3、C4两个通道的脑电信号利用Burg算法提取脑电信号的5阶AR模型系数作为特征并采用SVM分类器获得了较好的识别结果。从图8可以看出在高信噪比条件下，本文所提方法可以得到与文献[14]接近的分类性能，并优于文献[13]的方法。而当信噪比低于25 dB时，本文所提方法的分类性能明显优于其它两种方法，表明所提方法在低信噪比情况下具有更强的鲁棒性。究其原因在于因子分析模型可以看成是主成分分析模型的一种推广方法，主成分分析是通过线性组合的方式将原始数据综合成几个主分量，从而用综合后较少的主分量代替原始高维数据实现噪声抑制，这种综合的依据就在于原始高维数据之间存在一定的相关性，而这种相关性是通过不能直接观测到而又能够影响观测数据变化的公共因子体现，这些公共因子即因子分析模型中的隐变量，也就是说因子分析模型不仅能够实现噪声抑制，同时能够提取数据中包含的隐含信息，因此具有更好的分类性能。同时SVM分类器是在统计学习理论中的VC维和结构风险最小化原理的基础上建立的，相对于线性分类器在解决小样本，非线性及高维模式分类问题中表现出特有的优势。

图8   不同方法分类结果随信噪比变化

图9给出了不同信噪比条件下，分别利用所提因子分析模型、小波方法和PCA方法进行噪声抑制得到重构信号后提取前述三维功率谱特征并利用SVM分类器进行分类的结果。可以看出，在低信噪比条件下（SNR<25dB），所提方法对分类结果的提升最为明显，并且在信噪比高于10 dB时，所提方法即可获得优于80%的正确分类结果，明显优于小波方法和PCA方法在低信噪比条件下对分类结果的提升。利用PCA进行噪声抑制时，主分量个数的确定通常采用AIC或BIC准则，而已有试验结果表明，AIC确定的主分量个数较大，导致噪声抑制不彻底，BIC确定的主分量个数较小，在噪声抑制的同时会对信号分量产生影响。采用小波方法进行噪声抑制时，小波基函数的选取，阈值的确定和分解层数等对噪声抑制结果影响较大，目前没有最优的方法实现对上述参数的设置，而所提基于VBEM算法的因子分析模型是基于数据驱动，能够自适应的确定因子个数，具备精度高，收敛性好的优势，因此可以获得更好的噪声抑制性能。

图9   不同去噪方法对分类性能的影响

4   结  论

脑电信号的非线性、非平稳性和微弱性导致对运动脑电信号进行分类识别时存在特征提取困难，低信噪比条件下鲁棒性差，分类性能不好等问题。针对运动想象脑电信号的模式分类问题，重点对噪声抑制预处理和特征提取两个维度进行了研究，提出了一种基于因子分析模型的噪声稳健分类方法，首先利用因子分析模型对脑电信号进行预处理，滤除其中包含的噪声分量，在此基础上将时域信号转换至功率谱域，提取三维功率谱特征，最后利用SVM分类器对特征向量进行分类可以得到93.3%的分类结果，并且在SNR高于10 dB时即可得到优于80%的分类结果，极大的提高了低信噪比条件下的鲁棒性。相对于其它对比方法具备明显优势。

参 考 文 献

[1]    PFURTSCHELLER G，NEUPER C，GUGER C，et al. Current trending Graz brain-ccomputer interface（BCI）research[J]. IEEE Transactions on Rehabilitation Engineering，2000，8（2）：216—219.

[2]    WOLPAW J R，BIRBAUMER N，MCFARLAND D J，et al. Brain-computer interfaces for communication and control[J]. Clinical Neurophysiology，2002，113（6）：767—791.

[3]  KEVRIC J，SUBASI A. Comparison of signal decomposition methods in classification of EEG signals for motor-imagery BCI system[J]. Biomedical Signal Processing and Control，2017，31：398—406.

[4]    杜蘭，史蕙若，李林森，等.基于分数阶傅里叶变换的窄带雷达飞机目标回波特征提取方法[J]. 电子与信息学报，2016，12（38）：3093—3099.

[5]   KAR A，HANE C，MALIK J. Learning a multi-view stereo machine[C]. Advances in Aeural Information Processing Systems，2017：365—376.

[6]    段锁林，尚允坤，潘礼正.多类运动想象脑电信号特征提取与分类[J]. 计算机测量与控制，2016，24（2）：283—287.

[7]    BURKE D P，KELLY S P，DE CHAZAL P，et al. A parametric feature extraction and classification strategy for brain-computer interfacing[J]. IEEE Trans on Neural System Rehabilitation Engineering，2005，13（1）：12—17.

[8]    徐宝国，宋爱国，费树岷.在线脑机接口中脑电信号的特征提取与分类方法[J]. 电子学报，2011，39（5）：1025—1030.

[9]    ANDERSON C W，STOLZ E A，SHAMSUNDER S. Multivariate auto regressive models for classification of spontaneous electro encephalographic signals during mental tasks[J]. IEEE Trans on Biomed Engineering，1998，45（3）：277—286.

[10]  TIPPING M E，BISHOP C M. Probabilistic principle component analysis[J]. Journal of Royal Statistical Society，1999，61（3）：611—622.

[11]  YILDIZ A，AKIN M，POYRAZ M，et al. Application of adaptive neuro-fuzzy inference system for vigilance level estimation by using wavelet entropy feature extraction[J]. Expert System Application，2009，36（4）：7390—7399.

[12]  HUANG N E，SHEN Z，LONG S R，et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A：Mathematical，Physical and Engineering Sciences，2003，33（2）：903—915.

[13]  FLANDRIN P，RILLING G，GONCALVES P. Empirical mode decomposition as a filter bank[J]. IEEE Signal Processing Letters 2001，11（2）：112—114.

[14]  徐宝国，宋爱国.基于小波包变换和聚类分析的脑电信号识别方法[J]. 仪器仪表学报，2009，30（1）：25—28.

[15]  段锁林，尚允坤，潘礼正.多类运动想象脑电信号特征提取与分类[J].计算机测量与控制，2016，24（2）：283—287.