基于改进BBO算法的分数阶PID控制器设计

吴正平　尹凡　汪昊

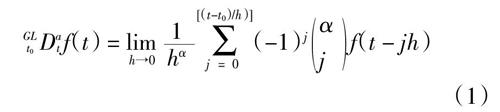
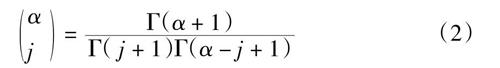
摘   要：针对分数阶PID（Fractional-Order Proportional-Integral-Derivative，FOPID）控制器参数整定，提出了一种改进生物地理学优化（Biogeography-Based Optimization，BBO）算法。该算法改进点主要包括：迁移操作中保留精英个体;变异操作中引入差分进化（Dtferential Evolution，ED）算法的变异策略;消除重复样本。仿真结果表明：在分数阶PID控制器参数整定中，与原始的BBO算法、遗传算法（Genetic Algorithm，GA）和粒子群算法（Particle Swarm Optimization，PSO）比较，提出的改进BBO算法具有超调量小、误差小，收敛更快的特点。

关键词：分数阶PID控制器;参数整定;生物地理学优化算法;差分进化算法

中图分类号：TP273;TP301.6                       文献标识码：A

Design of Fractional-order PID Controller Based

on Improved BBO Algorithm

WU Zheng-ping1，YIN Fan1？覮，WANG Hao2

（1. China Three Gorges University，Yichang，Hubei 443002，China;

2. State Grid Hubei DC Inspection and Transportation Company，Wuhan，Hubei 430050，China ）

Abstract：An improved Biogeography-Based Optimization（BBO） algorithm is proposed for parameters tuning  of fractional-order proportional-integral-derivative（FOPID） controller. The main improvement points of this algorithm include： retaining elite individuals in migration operation; introducing mutation strategy of differential evolution（DE） algorithm into mutation operation; eliminating duplicate samples. The simulation results show that compared with the original BBO algorithm，genetic algorithm（GA） and particle swarm optimization（PSO） algorithm，Improved BBO algorithm proposed in this paper has the characteristics of small overshoot，small error and faster convergence in parameter tuning of fractional order PID controller.

Key words：fractional-order PID controller;parameter tuning;BBO algorithm;DE algorithm

近年來，由于大量的实际控制系统可以用分数阶微分方程来表示，一些研究学者对分数阶控制器给予了极大的关注[1]。对比传统的PID控制器，分数阶PID控制器增加了两个可调节参数，使得控制器调节的范围增加，系统的稳定性和鲁棒性能够得到更好的控制。

由于附加的两个参数使得控制器参数优化变得更加复杂，国内外围绕FOPID控制器参数整定进行了大量研究。Bingul等人在文献[2]中使用粒子群算法（PSO）和人工蜂群算法（ABC）对FOPID控制器进行参数整定，仿真结果表明人工蜂群算法优化的分数阶控制器鲁棒性更好，在各种评价函数下展现出更良好的优越性。文献[3]提出了一种基于无人机滚转角控制的改进平面相位裕度的FOPID控制器设计方法。文献[4]在粒子群优化算法的变异操作中加入加速度因子，改进的MPSO算法可以有效地整定FOPID控制器参数。文献[5] [6]中，高嵩和金滔等人均对粒子群算法的惯性权重系数的改进，改进后算法优化FOPID的参数较PSO算法具有更高的收敛速度和精度。文献[7]提出将变异算子F和交叉算子CR进行自适应调整，提高了差分进化算法的参数优化速率和收敛性能，优化后的伺服系统具有良好的动态响应。杨博等人引入最优无源分数阶PID控制机制，采用改进的群灰狼优化算法优化控制器参数，提高了控制器的控制精度[8]。

给出了一种改进的生物地理学优化算法来优化FOPID控制器参数。将该算法与其他智能算法进行了仿真对比分析，仿真结果表明，该FOPID控制器的控制效果具有收敛速度快、误差小的特点。

1   分数阶PID控制器设计

1.1   分数阶微积分

对于给定函数f（t）， Grünwald-Letnikov定义的分数阶导数公式为：

（1）

式中，α为导数阶次，区间[a，t]为积分上下限，h为步长，[（t - t0）/h]表示取整。由Gamma函数可知二项式系数：

1.2 控制器设计

分数阶PIλDμ控制器由斯洛伐克学者Podlubny教授在1999年提出[9]，其典型控制器Gc（s）表达式如下：

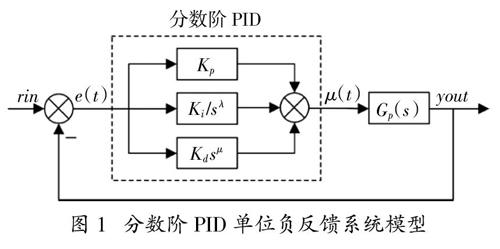
相比传统的PID控制器，分数阶PID控制器增加了两个可调参数λ和μ，λ为控制器积分项指数，μ为微分项指数，且0 < λ，μ < 2。控制器整定参数维度增加到5个，其形式更加灵活，相对传统PID控制器控制效果更好，同时增加了参数整定的复杂性。

图1   分数阶PID单位负反馈系统模型

对于FOPID控制器的设计，其中不确定参数 Kp，Ki，Kd，λ，μ的整定是关键。

2   分数阶PID参数整定

2.1   生物地理学优化算法

生物地理学优化（BBO）算法是在粒子群算法（PSO）[10-11]、遗传算法（GA）[12]基础上发展起来的，由美国学者Dan Simon最先提出[13]。生物种群栖息地的地理区域具有较高的适宜度指数（Habitat suitability index，HSI），影响其大小的因素称为适应性指数变量（Suitability index variable，SIV）。与所有进化算法相似，生物地理学优化算法的两个主要步骤是：迁移和变异。

（1）迁移操作

BBO算法的迁移操作指的是通过不同群体之间的迁入和迁出操作进行信息共享。栖息地物种数量的大小会影响种群数量的迁入率和迁出率。物种迁入迁出的数学模型主要有线性、二次、余弦和指数等四种模型。由于余弦模型更符合自然界的客观规律，使得算法性能更优越，所以本文选择了余弦迁移模型[14]。

图2   物种迁移余弦模型

物种迁移余弦模型如图2所示，I为最大物种迁入率，E为最大物种迁出率，S0为平衡态时的物种数。当迁入率为零时，栖息地能容纳的最大物种数为Smax。迁入率λi和迁出率μi（i = 1，2，…，n）的表达式如式（4）：

λi = I/2 × [cos（πSi /Smax） + 1]μi = E/2 × [-cos（πSi /Smax） + 1]       （4）

（2）变异操作

突发事件的出现可能会改变栖息地的种群数量变化，BBO算法定义为变异，变异操作可以提高栖息地的HSI。 表示种群规模， 表示种群数量为 时的概率， 满足如条件式（5）：

Pi′=-（λi + μi）Pi + μi+1Pi+1，i = 0-（λi + μi）Pi +λi-1Pi-1+ μi+1Pi+1，1≤i≤N-（λi + μi）Pi +λi-1Pi-1，i = N  （5）

BBO算法对应种群中每个解HSI的变异率 与物种数量概率 成反比：

gi = gmax（1 - Pi /Pmax），i = 1，2，…，n    （6）

式中，gmax为最大突变率，Pmax指栖息地最大物种数量概率。这种突变模式会增加种群的多样性，使低HSI的解决方案可能发生突变，可以提高算法的有效性。

2.2   改进BBO优化方法

BBO算法在迭代后期阶段会出现收敛速度变慢，动力不足的现象，故对该算法进行如下改进。

（1）保留精英个体

在使用迁移算子之前选出适应度最大的个体，直接传递给下一代，这样避免迁移算子破坏其优良性，加快算法收敛的速度。

（2）消除重復样本

算法在迭代的过程中随机出现的重复个体需要进行重复运算，延长了迭代的时间。IBBO算法进行了消除重复样本的操作，增强了种群多样性。

（3）差分进化变异策略

采用差分进化算法的变异策略，在IBBO算法的变异操作中加入缩放因子F，使算法的寻优能力增强。具体而言，本文选取文献[15]中的DE/best/2变异策略，在第g次迭代中，从种群中随机选取4个种群个体Xp1（g）、Xp2（g）、Xp3（g）、Xp4（g），且种群关系满足p1≠p2≠p3≠p4≠i，Xbest（g） 则是其中最优的个体。生成的变异向量如式（7）所示。

Vi（g）=Xbest（g）+F（Xp1（g）-Xp2（g））+

F（Xp3（g）-Xp4（g）），（0≤F≤2）     （7）

2.3   改进BBO算法步骤

通过对基本的BBO算法的改进得到IBBODE，图3所示为IBBODE算法的流程图，其主要步骤如下：

（1）初始化基本参数，这些参数主要包括：最大迁入率I，最大迁出率E，最大物种数为Smax，待求参数取值范围，栖息地数量N，迁移概率Pmodify，变异概率Pmutate。在此基础上计算适应度指数变量SIV。

（2）计算评价指标：计算并排序物种适应度指数HSI。

（3）迁移操作：进化开始，选取精英个体，计算栖息地迁入率、迁出率，进行迁移操作。

（4）变异操作：选择DE变异策略进行变异操作。

（5）终止条件：判断是否达到迭代次数，若是，则转到（6）;反之，转到步骤（2）。

（6）输出结果：输出优化参数向量和最优适应度指数值。

图3   IBBODE算法的流程图

3   仿真实例研究

假设被控对象为二阶系统，其传递函数为：

G0 = ■    （8）

選取ITAE性能准则作为目标函数F（x），其定义如下：

F（x） = min（s）       （9）

ITAE ： s = ■te（t）dt       （10）

FOPID整定参数为Kp，Ki，Kd，λ，μ，其取值范围定义为：

0≤Kp，Ki，Kd≤100≤λ，μ≤2     （11）

仿真条件为：对于改进BBO、GA、PSO三种算法，种群大小均取为60，为了便于比较，设最大迭代次数为50。对于GA，取交叉概率Pc为0.9;对于PSO，学习因子c1、c2为1.5，惯性权重Weight取为0.8;对于BBO，迁移概率Pmodify设为1，变异概率Pmutate设为0.05，精英个数取2，个体的最小迁入率lambdaL为0，最大迁入率lambdaU为1，步长dt为1，每个栖息地的最大迁入率I和最大迁出率E均为1; 对于IBBODE，取差分缩放因子F为0.6，变异概率C为0.2。

仿真结束，图4（a）、4（b）分别为不同优化算法下，系统的响应曲线和误差曲线，性能指标如表1所示。

综合图4（a）和图4（b）和表1可以看出，在分数阶PID参数寻优的过程中，GA和PSO算法超调较大，有明显的局部收敛;在算法迭代过程中，IBBODE算法的最小误差最小，说明其HSI最优。由表2可知，IBBODE算法的调节时间最短，说明系统更快速地达到了稳定。对比BBO和IBBO，IBBODE算法在快速性和稳定性都表现得更优越。

time（s）

图4（a）   不同优化算法的单位阶跃响应曲线

进化次数

图4（b）   不同优化算法最小误差迭代过程曲线

4   结   论

针对分数阶PID控制器参数整定问题，提出了使用改进生物地理学优化算法IBBODE来进行参数整定的方案。相比其他算法，本算法有如下改进优点：①在原有BBO算法的迁移策略中保留了精英个体;②消除重复样本的操作保证了种群多样性;③变异操作中使用了差分进化算法的变异策略，其缩放因子避免了算法陷入局部最优，提高了寻优速度。

通过仿真分析，改进的BBO算法与BBO算法、GA算法和PSO算法相比，在分数阶PID控制器参数整定时，所设计的控制器具有更快的收敛速度和更高的收敛精度。

参考文献

[1]    ZHANG Feng-xue，YANG Chun-hua，ZHOU Xiao-jun，et al. Fractional-order PID controller tuning using continuous state transition algorithm[J]. Neural Computing & Applications，2016：1—10.

[2]    BINGUL Z，KARAHAN O. Comparison of PID and FOPID controllers tuned by PSO and ABC algorithms for unstable and integrating systems with time delay[J]. Optimal Control Applications and Methods，2018.

[3]    SEYSDTABAII S. New flat phase margin fractional order PID design： Perturbed UAV roll control study[J]. Robotics and Autonomous Systems，2017，96：58—64.

[4]    AGHABABA M P. Optimal design of fractional-order PID controller for five bar linkage robot using a new particle swarm optimization algorithm[J]. Soft Computing，2016，20（10）：4055—4067.

[5]    高嵩，王磊，陈超波，等. 一种改进粒子群优化的分数阶PID参数整定[J]. 控制工程，2017（10）：44—49.

[6]    金滔，董秀成，李亦宁，等. 改进的粒子群优化算法优化分数阶PID控制器参数[J/OL]. 计算机应用：1—6.

[7]    王璇，史乐珍. 基于改进自适应DE算法的分数PI～λD～μ参数优化[J]. 工业仪表与自动化装置，2017（06）：116—119+123.

[8]    杨博，束洪春，朱德娜，等. 基于群灰狼优化的光伏逆变器最优无源分数阶PID控制[J]. 控制与决策：2018.1—11.

[9]    PODLUBNY I. Fractional-order systems and PI～λD～μ controllers[J]. IEEE Transaction on Automatic Control，1999，44（1）： 208—214.

[10]  VENTER G，SOBIESZCZANSKISOBIESKI J. Particle swarm optimization[J]. AIAA journal，2013，41（ 8）：129—132.

[11]  WANG D，TAN D，LIU L. Particle swarm optimization algorithm： an overview[J]. Soft computing，2018，22（2）：387—408.

[12]  周现甫. 遗传算法的原理及应用[J]. 科技展望，2017，27（3）： 265.

[13] DAN SIMON，Biogeography-Based Optimization [J]. IEEE Transactions on Evolutionary Computation，2008，12（6）：702—713.

[14]  MA Hai-ping. An analysis of the equilibrium of migration models for biogeography-based optimization[J]. Information Sciences. 180 （2010）： 3444—3464.

[15]  QIN A K，HUANG V L，SUGANTHAN P N. Differential evolution algorithm with strategy adaptation for global numerical optimization[J]. IEEE Transactions on Evolutionary Computation，2009，13（2）：398—417.