一种基于给定目标节点的个性化PageRank算法设计

易黎

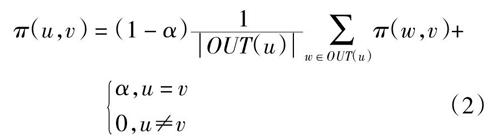
摘   要：以往衡量图网络节点重要性时，多基于给定源节点，计算该节点到其余目标节点的个性化PageRank值并推出重要目标节点，运算效率低且存储量大。基于此，提出了一种基于给定目标节点的个性化PageRank算法（TPPR），该算法结合本地更新与优先队列算法，通过计算从所有源节点到给定目标节点的个性化PageRank值来推出重要源节点，相较于传统算法运算精度更高，运行时间大幅减少。

关键词：个性化PageRank;目标节点;本地更新算法;优先队列算法

中图分类号：TP39                                             文献标识码：A

Design of A Personalized PageRant Algorithm Based on A Given Target Node

YI Li？覮

（Nanjing Fiberhome Xingkong Communication Development Co.，Ltd.，Nanjing，Jiangsu 210019，China）

Abstract：When the importance of the graph network node was measured，the personalized PageRank value of the node to the other target nodes was calculated based on the given source node，and the important target node was launched，which has low computational efficiency and large storage capacity. Based on this，this paper proposes a personalized PageRank algorithm （TPPR） based on a given target node. This algorithm combines the local update and priority queue algorithm to derive important information by calculating the personalized PageRank value from all source nodes to a given target node. The source node is more accurate than the traditional algorithm，and the running time is greatly reduced.

Key words：personalized PageRank;target node;local update algorithm;priority queue algorithm

PageRank是衡量圖网络节点重要性的指标之一，个性化PageRank算法（以下简称PPR）作为普通PageRank算法的扩展，通常直接用于依据用户偏好对其进行个性化的结果推荐，并及时反馈与用户搜索密切相关的结果信息[1]。PPR算法自Page等[2]提出以来，已被广泛应用于个性化搜索[3]、用户影响力排名[4]、网址链接预测[5]等各种数据集可表示为图结构的搜索场景中。

从相关研究来看，在计算PPR值时多采用蒙特卡罗或幂迭代算法。例如，A.Benczur和K.Csalogany[6]提出采用蒙特卡罗法计算从单个源节点到目标节点的PPR值，但由于存在大量的目标节点，计算成本较高，并且对于单个目标节点 而言，这种方法都需要计算N次，大大降低了计算效率。Fogaras[7]等研究发现采用幂迭代算法计算PPR值时，仅针对n个节点，至少也需要 的存储空间，并且在实际应用中，用户的偏好可能为图中任意节点的组合，因此图中至少需要包括 个任意节点子集。以往的PPR算法都是研究基于给定单个源节点来确定链接图中节点的重要性或权威值，反映与用户偏好相关的查询结果，缺乏对于给定目标节点，计算出所有源节点到该目标节点的个性化PPR值的相关研究工作，也无法基于某个给定目标节点逆向反推对其关注或感兴趣的用户。另外，传统算法需要在查询期间依据用户的偏好信息进行实时运算，在占用大量存储空间的同时，运算效率也严重降低。

据此，提出了基于给定目标节点v的PPR算法（以下简称TPPR）：给定有向或无向图G = （V，E）中的目标节点v，计算从所有源节点u∈V到目标节点v的PPR值π（u，v），如果边代表兴趣或支持，这个算法即表示为寻找所有对目标节点v感兴趣或支持的源节点u。这个算法也可被广泛应用于实际案例，例如重要客户挖掘、重点人员推荐等。此外，本算法模型也可在综合评价和信任系统中应用。

1   传统PPR算法

个性化PageRank算法继承了经典PageRank算法的思想，利用数据模型（图）链接结构来递归计算各节点权重，模拟用户通过点击链接随机访问图中节点的行为，即基于随机游走模型计算稳定状态下各节点得到的随机访问概率[8]。给定一个有向或无向图G = （V，E），在图G中，V表示所有网络节点的集合，E表示网络节点间的所有边，假设G为非加权图，定义节点u的入度为IN（u） = {w：（w，u）∈E}，出度为OUT（u） = {w：（u，w）∈E}。对于u，v∈V传统PPR算法的目标是计算从给定源节点到其余所有目标节点的PPR值。用户从源节点u开始随机游走，以概率α随机选择下一个访问节点，或者跳转到任意一个节点以（1-α）的概率开始新一轮的随机游走。经过多轮游走之后，每个节点被访问到的概率也会收敛趋于稳定，所以从源节点u到目标节点v的PPR值可以解释为在随机游走过程中停止在节点v的稳定概率，即π（u，v） = P[XL = v]。在稳定状态下，用户所偏好的那些节点和相关的节点总能够获得较高的访问概率。传统个性化PageRank的随机游走模型可形式化地表示为：

r = （1 - α）Mr + av        （1）

其中，M为图G对应的邻接矩阵，v为用户的偏好向量，v = 1，反映图中每个节点针对给定偏好向量的重要性，r为M的特征向量。

2   TPPR算法设计

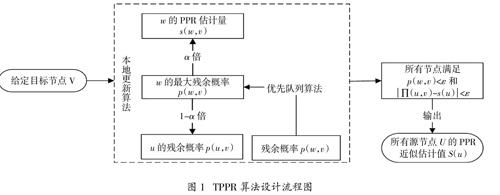
TPPR算法不同于传统PPR算法，它是为了计算所有源节点u到给定目标节点v的PPR值。给定目标节点v，该算法在执行过程中使用本地更新算法与优先队列算法进行改进，使得其在不需要访问所有节点的情况下，计算出其所有源节点u的PPR值π（u，v）的近似估计值，并且满足给定的误差阈值范围。TPPR算法设计流程图如图1所示。

2.1   本地更新算法

根据PPR算法的随机游走模型可以推出本地更新算法：假设源节点具有一定的“概率质量”，然后从该源节点开始“概率质量”推送，并迭代进行推送过程，直到满足设定的误差阈值时，停止概率推送过程，最终得到每个节点的PPR值。在本地更新过程中，每个节点需要维持两个属性：PPR估计量 s（u）和残余概率p（u），其中s（u）表示该节点收到并且已经推送出去的“概率质量”，p（u）表示该节点上收到但还没有被推送出去的“概率质量”。本地更新算法只作用于目标节点的相关邻近区域，而无需访问整个图网络的所有节点。TPPR算法主要采用了逆向推送的本地更新算法，即从给定的目标节点 v出发，对π（u，v）进行逆向推送操作，最终计算出每个源节点u到给定目标节点v的PPR估计值。从u开始的随机游走是通过立即传送或通过跳转到一个随机邻节点开始的，所以从u到v的预期概率为非直接传送次数的概率，即从u的外邻居节点u∈OUT（u）到达v的平均期望次数的概率。该算法思想主要基于PPR算法的递推公式：

π（u，v） = （1 - α）■■π（w，v）+

α，u = v0，u≠v        （2）

其中，源节点为u，目标节点为v，w为u的外邻居节点（u指向w），由于α表示在每个节点终止游走的概率，当u = v时到达给定目标节点，所以在公式中加入α。TPPR算法可以被视为从给定的目标节点v开始的“概率质量”推送算法，算法在逆向推送过程中每个节点维持PPR估计量s（w，v）和残余概率p（w，v）两个变量，而每一步逆向推送回溯过程，可以理解为将该节点p（w，v）的α倍残余概率推送增加至该节点的s（w，v），剩下的1-α倍残余概率平均的逆向回溯给节点w的每个入链节点 u∈IN（w）的p（u，v）。

2.2   优先队列算法设计

在TPPR算法中加入优先队列算法，随着节点变化不断更新节点的概率值时，改进后的算法只需要推送自上次w概率推送以来改变的最大部分，这样可以大大节省算法的运行时间和存储空间。TPPR算法主要基于给定目标节点v进行概率逆向推送操作，最终对每个源节点u计算一个PPR估计量s（u），来从低到高估计每个源节点u到给定目标节点v的PPR值π（u，v），并且随着网络的动态变化不断更新。因此，算法的基础更新步骤为节点w的当前PPR估计量s（w）与其最后一次概率推送之间的差异用残余概率p（w）表示，将p（w）排序形成优先级队列Q，以至于可以轻易的找出p（w）中值最大的节点。优先队列算法的主要思想为只要存在某个节点的优先级高于设定阈值α∈ε，我们就移除具有最大优先级的节点，并将其概率推送回给它的内邻居节点，随后迭代执行此逆向推送过程，直到满足误差阈值条件时，结束迭代过程并输出结果。只要某个节点的优先级高于最小阈值，弹出优先级最高的节点，并将其概率进行推送。完整的优先级队列算法见算法1所示：

算法1：基于给定目标节点的个性化PageRank算法（TPPR算法）

输入：图G = （V，E），推送概率α，目标节点v，允许误差值ε

初始化：s[v] = p[v] = α

q = V中按残余概率p排序形成的最大优先级队列

While q.max priority（）>α∈ε，do

w = q.popMaxElement（）

for w的內邻居节点u（节点u指向节点w）：

Δs = （1 - α）■

若u不在s中：

s[u] = p[u] = 0

结束

s[u] = p[u] + Δs

q.increas Pr iority（u，p[u] + Δs）

结束for循环

p[w] = 0

结束While循环

输出：概率向量s（π（u，v））（的估计近似值）：对于所有源节点u，节点集合V→[0，1]，此时π（u，v） - s[u] < ε.

图2描述了优先队列算法在仅有四个节点包括给定目标节点v的图中的六次迭代过程。对于源节点u，s是π（u，v）的当前估计值，优先级p是残余概率。优先队列算法每次从优先级队列中取出 p（w）最大值进行逆向推送，直至所有节点都满足π（u，v） - s[u] < ε，即最终的PPR估计值与PPR实际值之间的偏差不超过阈值，其中填充灰色的节点表示下一步将要执行优先级传送操作的节点。

3   算法效果评估

3.1   误差分析

TPPR算法的一个核心问题是如何选择合适的优先级阈值来确定是否移除队列中的节点。首先考虑阈值ε，但这个阈值并不是足够小来确保所有的误差都小于ε。最终选择αε作为合适的阈值，当所有节点的优先级均小于αε时，优先队列算法运行完成，此时对于所有源节点u∈V，所输出的PPR估计值向量s满足π（u，v） - s[u] < ε。

3.2   平均运行时间

在最糟糕的情况下，目标节点v具有比其余所有节点的高PPR值，这需要对整个图进行分析。因此，给定运行时间的有效约束，分别对一般情况和糟糕情况进行分析。首先分析在一般情况下优先级队列算法的平均运行时间，此时随机均匀选择目标节点v。给定一個任意图G，允许误差值为ε，推送概率α。令n为图G中的节点数量，m为边的数量。v为从图G所有节点集合V中随机均匀选择的目标节点，故优先级队列算法将预期运行O（■（■ + log（n）））次。

蒙特卡罗方法在失败概率为δ的情况下，使用Chernoff边界计算π（u，v）近似值的平均时间复杂度为Θ■log■。如果图足够稀疏或足够小，算法的平均时间复杂度最多为O■■。因此，在计算所有节点的PPR估计近似值时，在每个节点运行优先队列算法比运行蒙特卡罗方法的效率要高很多。

4   实验案例

采用微博的社交网络图做实验，实验数据共包含75879个节点，508837条边，设置节点传送概率 α∈{0.1，0.2}，附加误差ε∈{10-4，10-5，10-6}，每次实验随机均匀选择100个目标节点v来运行优先队列算法。设定节点传送概率α = 0.1，误差阈值ε = 10-6。由于具有高全局PageRank值的节点经常相对于其他节点来说更可能成为目标节点，因此按全局PageRank概率选择100个目标节点 ，运行优先队列算法，在算法收敛后计算经验误差maxu∈Vπ（u，v） - s[u]。图3中为算法收敛之后经验误差占目标误差比例的分布直方图，从上图可以看出，最大的经验误差约为0.90ε，这与设定目标误差ε的界限非常接近，大部分经验误差通常超过设定目标误差ε界限的50%。

经验误差占目标误差的比例

图3   优先队列算法的经验误差

迭代次数

图4   优先队列算法的迭代次数

迭代次数和/DV（αε）

图5   迭代次数和与DV（αε）的比率分布

当设定传送概率α = 0.1，误差阈值ε = 10-5，随机均匀选择100个目标节点v，运行优先队列算法。图4为优先队列算法迭代次数，即内部循环中跳转节点优先级的次数。其中，x轴为指数刻度，垂直线为设置的平均运行次数界限。从图中来看，在满足误差阈值时，大部分节点的迭代次数都小于约束界限。

参数化分析显示，算法运行时间复杂度最多为O（■）log（■））。为了证明准确性，将迭代次数和Dv（αε）进行比较。当α = 0.1，ε = 10-5，根据公式推算迭代次数和与Dv（αε）的证明比率约为200，但在实验中平均比率小于4。比率的分布如图5所示。对于大多数节点，尽管在图4中迭代次数的绝对数量以指数刻度变化，但从图5来看算法迭代次数和与Dv（αε）的比率在2范围内。

表1   优先队列与幂迭代算法运行时间比较

为了体现优先队列算法的效率，使用幂迭代算法在相同设置下的运行结果作为基准。从表1来看，在设置α = 0.1，随机均匀选择100个目标节点条件下，优先队列算法的运行效率远高于幂迭代算法。

5   结 论

为了解决传统PPR算法在衡量图网络节点重要性时，只考虑基于给定源节点推荐重要目标节点、运算效率低等问题，提出了一种基于给定目标节点的个性化PageRank算法（TPPR）。TPPR算法在传统PPR算法的基础上加入本地更新算法和优先队列算法进行改进，改进后的算法一方面继承了个性化PageRank算法的思想，在节点关联搜索中考虑了用户在查询、收藏页面等个性化信息表达中的行为偏好影响，另一方面又实现了基于给定目标节点搜索重要源节点的算法方案设计。TPPR算法具备广泛的实用性，既可用于实际图结构搜索场景中发现对目标感兴趣甚至支持的用户，也相较于以往蒙特卡罗、幂迭代算法而言，运算精度与运算效率都具有大幅度提升。

参考文献

[1]    LIBEN-NOWELL D，KLEINBERG J. The link-prediction problem for social networks[J]. Journal of the American Society for Information Science and Technology，2007，58（7）：1019—1031.

[2]    PAGE L，BRIN S，MOTWANI R，et al. The PageRank citation ranking：bringing order to the web[R]. State of California，Stanford University，1999.

[3]    孟瑞玲. 个性化PageRank算法在图书馆智能搜索引擎中的实现[J]. 现代情报，2010，30（07）：93—96.

[4]    徐文涛. 社交网络中用户影响力及个性化排名相关技术研究[D]. 合肥：安徽大学，2017.

[5]    朱凡微，吴明晖，应晶. 高效个性化PageRank算法综述[J].中国科技论文，2012，7（01）：7—13.

[6]    BENCZUR A，CSALOGANY K，ARLOS T，et al. Spamrank-fully automatic link spam detection work in progress[C]. In Proceedings of the First International Workshop on Adversarial Information Retrieval on the Web，2005.

[7]   FOGARAS D，R？魣CZ B. Towards scaling fully personalized pagerank：Algorithms，lower bounds，and experiments [J]. Internet Mathematics，2005，2（3）：333—358.

[8]    刘记云. 基于MapReduce的个性化PageRank算法研究[D].哈尔滨：哈尔滨工程大学，2013.