基于差分变异算子的改进人工蜂群算法

张怡森

摘   要：文章针对传统人工蜂群算法收敛速度慢、精度不高的问题，基于差分进化算法中的变异算子，对人工蜂群算法搜索方程进行改进，在种群更新过程中引入当前种群最优个体信息，以提升算法的收敛速度和局部优化能力。

关键词：人工蜂群算法;搜索方程;变异算子

人工蜂群算法（Artificial Bee Colony，ABC）是由Karaboga基于蜂群搜索蜜源行为提出的一种群体智能优化算法，该算法在搜索过程中同时兼顾局部搜索和全局搜索，控制参数少、易于实现、全局收敛性能好、具有良好的鲁棒性，并且其优化性能优于其他一些传统智能优化算法[1]，如遗传算法、粒子群算法、差分进化算法等，特别是在非线性函数优化求解方面具有良好的性能。关于ABC算法的研究主要是对其选择机制和搜索方程进行改进，以提升算法性能。丁海军等[2]将boltzmann选择策略引入ABC算法，对其收敛速度和种群多样性进行平衡;毕晓君等[3]采用自由搜索算法中的信息素模型代替轮盘赌选择策略，提高了算法的全局搜索能力。在上述研究中由于没有对算法搜索方程进行改进，导致在处理复杂优化问题时收敛速度和寻优精度较低。因此，本文在对传统ABC算法分析基础上，考虑当前种群最优个体对种群更新的影响，对算法搜索方程进行改进，在数值实验中选用标准测试函数对算法性能进行验证。

1    人工蜂群算法

在ABC算法模型中，主要包含两部分：蜜源和人工蜂群。其中，蜜源位置代表优化问题的可行解，蜜源的花蜜量代表对应解的质量或适应度值。根据蜜蜂在搜索过程中的职能不同可将人工蜂群分为3类：采蜜蜂、观察蜂和侦查蜂。采蜜蜂和观察蜂数量各占蜂群一半，且等于蜜源数量，当采蜜蜂放弃对应蜜源后即成为侦查蜂。在ABC算法中，3类蜜蜂按以下顺序进行搜索：

（1）采蜜蜂对蜜源进行开采，评估花蜜量。在该过程中，采蜜蜂在蜜源附近搜索，并采用贪婪选择机制选择新蜜源位置以发现局部最优解。

（2）观察蜂对蜜源进行开采。根据采蜜蜂传递的蜜源信息，按照与花蜜量正相关的概率选择蜜源位置进行开采，同样地，采用贪婪选择机制选择新蜜源位置以发现局部最优解。

（3）确定侦查蜂。如果蜜源在经过一定次数后仍没有更新，说明该位置陷入局部最优。此时，采蜜蜂放弃该蜜源位置，相应的采蜜蜂变为侦查蜂。侦查蜂随机搜索新蜜源代替被放弃的蜜源。

在初始化蜜源位置基础上，ABC算法通过不断重复以上3种蜜蜂的活动搜索全局最优解。在上述ABC算法中，存在3个控制参数，描述如下。

（1）SN：种群数量。即种群中采蜜蜂和观察蜂的数量，且与蜜源数量相等。

（2）Limit：蜜源为更新次数。当蜜源循环次数超过Limit后仍没有改进，该蜜源位置被放弃，对应的采蜜蜂变为侦查蜂。

（3）Maxcycle：最大迭代次数。算法迭代次数大于Maxcycle时结束运行并输出最优个体。

在ABC算法优化过程中，首先随机产生SN个初始解，假设优化问题的每个解Xi，i=1，2，…SN，D为向量，D是优化变量个数。在此基础上，采蜜蜂和观察蜂通过以下搜索方程产生新蜜源（即新的可行解）：

2    改进人工蜂群算法

基于上述分析可知，ABC算法的优化性能主要受搜索方程影响。在搜索方程式（1）中，Xk为随机选择的个体，新的可行解是通过当前个体向另一个随机个体的偏移得到。这种方法产生的可行解质量不能保证，对当前解的更新效率较低，而且在搜索过程中没有充分利用种群最优个体信息。因此，ABC算法局部优化能力较差，导致算法的收敛速度较慢。

针对上述问题，本研究借鉴差分进化算法（Differential Evolution， DE）的变异算子对ABC算法搜索方程进行改进，以提高算法收敛速度。DE算法的变异算子充分利用了种群中最优个体的信息，可以使种群快速向最优个体聚拢，具有较强的局部优化能力。基于差分变异算子，新搜索方程为：

由上式可以看出，新的可行解只在最优个体附近产生，因此可以有效提高算法收敛速度。但采用该搜索方程也会在一定程度上降低种群的多样性，可能使得算法过早收敛，降低全局搜索能力。因此，为平衡算法的全局搜索和局部搜索能力，在采蜜蜂阶段采用式（1）产生新的可行解，尽可能扩展搜索区域，保证种群的多样性;由于观察蜂可以综合所有采蜜蜂得到的信息，进而判断出当前种群中最优个体位置，所以在观察蜂阶段，采用式（2）产生新的可行解，增强种群更新的趋势性。

3    数值实验

部分学者已对ABC算法与遗传算法、蚁群算法、粒子群算法等智能优化算法进行了较为详细的比较分析，因此这里只将本文提出的改进ABC算法（MABC）和原始ABC算法进行比较，验证MABC算法的性能和优越性。

为验证本文所提MABC算法的性能，选取3个不同类型的优化算法标准测试函数Sphere、Griewank和Rosebrock进行数值实验。表1给出了选用函数的函数名、表达式及搜索空间。Sphere为单峰高维函数，理论最优值为f（0，…，0）=0，设置维数为100，搜索空间为[-100，100]D;Griewank为多峰多极值的高维函数，理论最优值为f（0，…，0）=0，设置维数为100，搜索空间为[-600，600]D;Rosebrock为多峰少极值的低维函数，理论最优值为f（1，…，1）=0，设置维数为5，搜索空间为[-100，100]D。

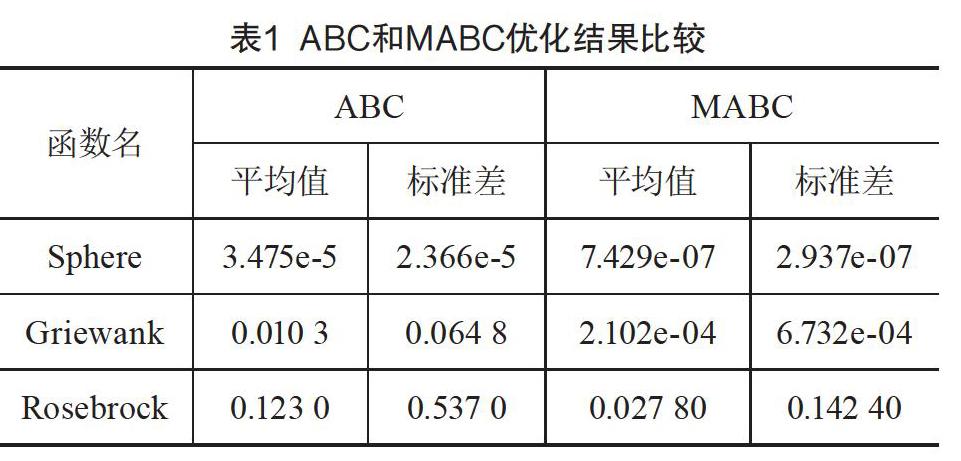
ABC算法和MABC算法控制参数设置相同，如下所示：SN=50，Limit=50，Maxcycle=1 000。为测试算法性能，在以上参数设置下对每个测试函数独立运行算法30次，计算优化结果的平均值和标准差。在此基础上比较算法的鲁棒性和寻优精度，并通过优化过程对算法收敛速度进行分析。不同函数优化结果的平均值和方差如表1所示。

由表1可以看出，针对实验中的3个测试函数，本文提出的MABC算法所得优化结果平均值和标准差均优于原始ABC算法。特别是在多峰函数Griewank和Rosebrock中，ABC算法优化结果精度较差，难以得到满意解。因此，本文提出的MABC算法能够有效提高寻优精度及结果的鲁棒性，具有良好的全局搜索能力。

为直观对比两种算法的收敛性能，下面对以上3个测试函数在ABC和MABC算法下的优化过程进行分析。对Sphere函数来说，MABC算法在迭代600次后趨于收敛，ABC算法在迭代800次后趋于收敛;对Griewank函数来说，MABC算法在迭代700次后趋于收敛，ABC算法在迭代900次后趋于收敛;而对于Rosebrock函数，MABC算法在迭代500次后趋于收敛，ABC算法在迭代700次后趋于收敛;可以看出，MABC算法的收敛速度明显更快。由此可得，与传统ABC算法相比，MABC算法能够有效提高种群更新效率和收敛速度，具有良好的函数优化性能。

4    结语

本文在ABC算法机理分析基础上，结合DE算法的变异算子，将每代种群中最优个体信息引入搜索方程，在一定程度上提高了种群更新效率，平衡了算法全局优化和局部优化能力。数值实验结果表明，本文所提的改进方法能够有效提高ABC算法收敛速度和优化结果精度。

[参考文献]

[1]KARABOGA D，AKAY B.A comparative study of artificial bee colony algorithm[J].Applied Mathematics and Computation，2009（1）：108-132.

[2]丁海军，冯庆娴.基于boltzmann选择策略的人工蜂群算法[J].计算机工程与应用，2009（31）：53-55.

[3]毕晓君，王艳娇.改进人工蜂群算法[J].哈尔滨工程大学学报，2012（1）：117-123.