基于时间序列Prophet模型的乘用车消费税预测
2020-04-09赖慧慧
◆赖慧慧
内容提要:运用时间序列模型预测未来的税收变化,对税收收入的组织、规划和决策具有重要的意义。为探索一种更为有效的方法来提高季节性行业的消费税预测准确率,文章采用基于可分解(趋势+季节+节假日)的Prophet模型,对2014—2019年不同排量乘用车消费税数据进行训练和测试,并运用2019年7—12月的乘用车消费税数据进行推算预测和实证分析,三类不同排量乘用车预测的平均误差分别为24.97%、5.70%、39.85%;若剔除12月,则平均误差分别为2.86%、4.90%、8.48%。这就给分行业分品目的税收预测提供了一种新思路。
一、引言
税收预测是指运用统计学、经济学等原理和方法,通过分析一定阶段的税收历史数据,对未来税收收入的发展趋势及规律的预见和推断。从微观上看,税收预测有利于提高组织收入的科学性,堵塞征管漏洞,降低税收流失率;从宏观上看,精准的税收预测有利于完善财税体制,合理安排财政预算,有效发挥税收在国家治理中的基础性、支柱性和保障性作用。近年来,随着大数据技术的运用,大量数据模型被应用到税收预测中,但大多集中在宏观层面,即总体的税收收入、分税种收入等;在中观层面,即通过研究行业的运行规律来预测分行业、分品目税收收入的文献较少。随着税收信息化建设的不断推进,税务部门掌握了大量的税收历史数据,使得分行业分品目的税收预测成为可能。相比其他税种,消费税收入较为稳定,尤其是在汽车制造业,由于技术和投资壁垒高,企业进入和退出成本高昂,一旦建成投产,产能稳定,往往能成为当地重点税源企业,提供稳定而充足的税源。同时,乘用车消费税收入属于时间序列数据,是同一属性在不同时间上的相继观察值排列而成的数列,但乘用车消费的变化趋势中季节性和节假日的影响也比较明显。如果能找到适合季节性和节假日的模型预测该行业的消费税,就能给分行业分品目的税收预测提供一种新思路。
二、文献回顾
通过研究时间序列,我们能够描述事物过去的状态,分析事物发展变化的规律,并对未来进行预测。时间序列预测一直是预测当中的难点,人们很难找到一个适用场景丰富的通用模型。这是因为现实中每个预测问题的背景知识往往是不同的,即使是同一类问题,影响这些预测值的因素也往往不同,使得时间序列预测问题变得尤其复杂。1968年Box和Jenkins提出了一套比较完善的时间序列建模理论和分析方法。这些经典的数学方法通过建立随机模型,如自回归模型、自回归滑动平均模型、求和自回归滑动平均模型和季节调整模型等,进行时间序列的预测。这些模型只适用于平稳时间序列,本质上只能捕捉线性关系,而不能捕捉非线性关系。
当前,时间序列预测主要采用的方法有支持向量机、神经网络、ARMA模型等。支持向量机通过核函数实现样本空间到高维特征空间的非线性映射,主要处理小样本的数据。王革丽(2008)基于支持向量机的“升维”思想对时变控制参数条件下Lorenz系统产生的非平稳时间序列进行研究。针对税收收入预测不稳定、非线性、动态开放性的特点,常青(2007)和张玉尹(2011)提出了支持向量机的税收收入预测方法,并应用于实际税收收入情况的预测。
神经网络的方法包括模糊神经网络、径向基函数(RBF)网络、小波神经网络以及积单元神经网络等,主要通过学习进行非线性逼近,也往往用于时间序列数据的预测。沈存根(2011)运用BP神经网络建立税收预测模型,分析了产业增加值、固定资产投资总额、进出口总额、财政支出总量、居民消费水平等若干经济指标的变化对税收收入的影响。刘岩(2014)采用神经网络模型研究吉林省国税收入与地区生产总值、工业增加值、固定资产投资、社会消费品零售总额影响因子之间的关系,挖掘出影响吉林省国税收入的主要因素,并预测吉林省国税收入。
自回归移动平均模型ARMA是拟合平稳序列的模型,可分为AR模型、MA模型和ARMA模型三大类。赖慧慧(2019)运用ARMA模型对增值税销项税额进行预测,首先是对原始数据取对数、差分和分解的平稳性检测,发现分解能使序列达到平稳性要求,再将数据分解为残差、趋势和季节,通过白噪声检验,最后用加法模型得到原序列的预测序列。王静静等(2019)提出基于小波ARMA模型的预测方法,首先采用小波变换方法对非平稳离散的增值税销项税额时间序列进行消噪处理,并对去噪信号序列差分处理和平稳性校验,最后根据预测序列的自相关序列、偏自相关序列对小波ARMA模型进行初步定阶,对模型的适应性进行检验,得到增值税销项税额的最优小波ARMA模型。
然而,这三类方法对于具有季节性和节假日的数据预测效果不是很理想。因此,本文采用Facebook公司近年开发的基于STL分解思想的时间序列预测模型Prophet模型,对2014—2019年的乘用车三个品目消费税应征数进行分析,若剔除12月,预测的平均误差均小于10%,证明该模型在税收收入数据的预测中有着良好的效果。
三、基于STL分解思想的Prophet预测模型
本文采用了一种基于STL分解思想的Prophet预测模型,该模型是Facebook公司近年开发的时间序列预测模型,采用广义加法模型拟合平滑和预测函数,运行速度快,适用于具有明显内在规律的商业行为数据。Prophet预测模型还擅长处理具有异常值和趋势变化的周期数据,而乘用车销售数量具有很强的季节性。因此,本文采用Prophet预测模型对从2014年1月到2019年6月乘用车消费税进行训练,并对2019年7—12月数据进行预测。
STL分解是分解时间序列的预测模型,将时间序列分解为周期项(Season)、趋势项(Trend)、节假日项(Holiday)等。模型写成三部分之和(根据数据的内在机理),再拟合实际数据求解模型参数。本文使用的Prophet模型就是基于STL分解思路,模型可分解为三个主要组成部分:趋势、季节性和节假日。它们按如下公式组合:

其中:g(t)为趋势项,使用了两种趋势模型:饱和增长模型和分段线性模型,通过选择变化点来预测趋势变化,用于拟合时间序列中的分段线性增长或逻辑增长等非周期变化;s(t)是周期项,描述各种周期变化趋势,如每周或每年的季节性;h(t)有效纳入非规律性节假日效应,将特殊影响时间作为先验知识进行融合;∈t是服从正态分布的噪声因子,作为误差项反映未在模型中体现的异常变动。
图1是Prophet的整体框架,整个过程分为四部分:Modeling、Forecast Evaluation、Surface Problems以及Visually Inspect Forecasts。从整体上看,这是一个循环结构,而这个结构又可以根据虚线分为分析师操纵部分与自动化部分。因此,整个过程就是分析师与自动化过程相结合的循环体系,也是一种将问题背景知识与统计分析融合起来的过程,这种结合大大增加了模型的适用范围,提高了模型的准确性。按照上述的四个部分,Prophet的预测过程为:
(1)Modeling:建立时间序列模型。分析师根据预测问题的背景选择一个合适的模型。
(2)Forecast Evaluation:模型评估。根据模型对历史数据进行仿真,在模型的参数不确定的情况下,我们可以进行多种尝试,并根据对应的仿真效果评估哪种模型更适合。
(3)Surface Problems:呈现问题。如果尝试了多种参数后,模型的整体表现依然不理想,这个时候可以将误差较大的潜在原因呈现给分析师。
(4)Visually Inspect Forecasts:以可视化的方式反馈整个预测结果。当问题反馈给分析师后,分析师考虑是否进一步调整和构建模型。

图1 Prophet的整体框架
实验流程如图2,将原始数据集进行预处理,分为训练数据和测试数据,对Prophet预测模型进行训练和测试,完成训练后可用于乘用车消费税的预测。
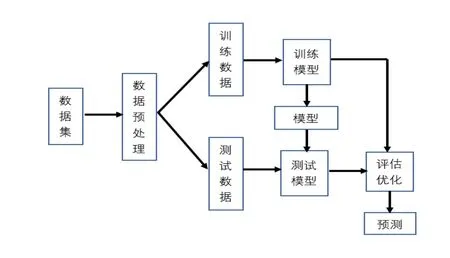
图2 实验流程
四、实证结果分析
在获取某地区2014年1月至2019年6月乘用车3个品目的消费税应征数后,首先进行数据预处理:对原始数据取自然对数,以缩小数据的绝对数值,使数据更加平稳,消弱数据的波动性。使用集训练、测试、优化为一体的Prophet模型,并用样本集测试训练得到模型效果。
品目1:2014年1月至2019年6月,1.0升<气缸容量≤1.5升的乘用车消费税
品目2:2014年1月至2019年6月,1.5升<气缸容量≤2.0升的乘用车消费税
品目3:2015年3月至2019年6月,2.0升<气缸容量≤2.5升的乘用车消费税
(一)时间序列数据分析
使用Prophet模型对品目1进行分解,图3显示了品目1的分解序列。图3中上图是使用分段线性函数拟合得到的时间序列非周期变化曲线,表示增长趋势,显示税收稳步增长;下图是时间序列周期变化曲线,即每年的季节性变化周期。图4是品目1的时间序列拟合和预测图。

图3 品目1序列分解

图4 品目1序列拟合和预测
同样,图5、图6分别是品目2的序列分解图、序列拟合和预测图,图7、图8分别是品目3的序列分解图、序列拟合和预测图。

图5 品目2序列分解

图6 品目2序列拟合和预测

图7 品目3序列分解

图8 品目3序列拟合和预测
(二)模型误差
为了检验Prophet模型在乘用车消费税预测中是否有效,在运用2014年1月至2019年6月的数据进行训练建模后,对2019年7—12月的乘用车消费税进行预测,将预测值与实际值进行比较,计算出预测相对误差,作为衡量该模型的预测准确性的依据,结果见表1。

表1 2019年7月—12月分品目乘用车消费税预测相对误差
从各月预测情况来看,2019年12月的误差明显较2019年7—11月的误差大。这一方面是由于预测的月份越久,精度越差;另一方面也和年底调控因素有关。若剔除12月,从平均相对误差来看,品目1的准确性最高,误差最小,品目2次之,品目3的误差最大。三个品目的平均预测误差均在10%之内,其中品目1和品目2的误差在5%之内,而品目3的误差稍大。原因如下:一是品目3从2015年3月才有消费税收入,较品目1、品目2数据量更少;二是品目3较品目1、品目2的消费税收入基数更小;三是品目3属于大排量高档车,价格高,消费弹性大,和品目1、品目2的实用型中低档车相比,消费税收入更加不稳定。
五、研究结论与展望
文章运用了Facebook公司开发的Prophet模型,分析2014年1月至2019年6月的乘用车三个品目消费税收入数据,建立模型,预测了2019年7—12月消费税收入,得到乘用车三个品目消费税收入预测的平均相对误差分别为24.97%、5.70%、39.85%;考虑到最后一个月的调控因素,如剔除12月,则平均误差分别为2.86%、4.90%、8.48%,均在10%之内,证明Prophet模型具有较好的泛化能力,在具有季节性和节假日特征的税收预测上精度较高,具有优势。但也发现,对于数据样本小、收入不稳定的品目,预测精度有所下降。因此,Prophet模型更适用于全国或全省分税种、分行业、分品目的税收预测,而且应以尽可能多年份的历史数据为基础建立数据模型。
未来可以考虑使用Bagging思想,采用多个时间序列预测模型的集成,然后进行表决,进一步提升预测准确率。也可以对某一税种的所有行业进行分类,并对每种类型采用精度最高的时间序列预测模型,最后加总预测出该税种收入甚至全部税收收入。与以税基变量为基础的“自上而下”的税收预测相比,这种“自下而上”的税收预测方法,数据的可获得性更高,适应性更好,基础数据的质量也更容易评估,因此在税务部门有广阔的应用前景。
