SiH(X2Π)从头算解析势能函数和光谱常数

赵文丽，高峰，张红，曹学成

山东农业大学信息科学与工程学院，山东泰安 271018

SiH 自由基是许多化学反应(如硅烷分子裂解反应)的重要中间产物，它在诸多工业过程，如等离子气体沉积、薄膜构成以及半导体制造业方面有着重要的作用[1，2]。另外，SiH 自由基广泛存在于在星际物质[3]和恒星气体中(在太阳黑子的光谱中已得到证实[4，5])，其光谱数据已经成为天体物理学的重要参数。因此，不论是在天体物理学领域还是化学工程领域SiH 自由基都是重要的研究对象。

实验上，1930 年Jackson[6]首次采用光谱法观测到SiH 自由基。1931 年，Mulliken[7]对Jackson观测到的光谱进行了分析和部分修正。1980 年Perrin 和Delafosse[8]用硅烷辉光放电管测量了SiH 自由基发射光谱。1985 年Washida[9]在硅烷的真空紫外线光分解系统内观察到SiH 自由基(A2Δ→X2П)的发射光谱。1987 年Seebass[10]通过激光磁共振观测到了SiH 自由基5 个同位素的红外光谱，并且观察到了SiH 基态(X2П)的自旋和轨道耦合效应。1998 年Ram[11]用高分辨率的傅里叶变换光谱仪观测到了SiH 自由基的发射光谱。这些实验报道了SiH 自由基的光谱常数和分子特性。

理论上，1967 年Cade 和Huo[12]首次运用从头算方法给出SiH 自由基的光谱常数，并用Hartree-Fock 方法计算了SiH(X2П)的光谱常数。1971 年Wirsam[13]结合自洽场分子轨道和组态相互作用(CI)方法计算SiH 自由基六个态的光谱性质，其中三个态当时还没有实验数据报道。1983 年Lewerenz 和他的合作者[14]用多参考双激发组态相互作用(MRD-CI)方法计算了SiH 自由基10 个态的势能曲线(PECs)。施德恒等于2008 年采用单双体三激发耦合簇(CCSD(T))方法研究了SiH(X2П)的光谱常数，又于2013 年使用多参考组态相互作用(MRCI)方法计算了SiH(X2П，A2Δ，B2Σ-，C2Σ+，D2Σ+，F2П and a4Σ-)的势能曲线和光谱常数[15，16]。这些理论研究报道了SiH 自由基的部分态的光谱常数。

1 理论

1.1 从头计算

我们选用MRCI(Q)和戴维孙修正方法[17]进行从头算，用aug-cc-pVXZ(AVXZ)和aug-ccpV(X+d)Z(AVXdZ)(X=Q，5，6)的基组，由Molpro2012 软件包计算得到所有从头算能量点。采用C2v点群对称进行计算，其中包含四个不可约表示，即A1，A2，B1 和B2。计算中将9 个分子轨道(MO)确定为活化空间(4-8σ和2-3π轨道)，他们包含5 个a1，2 个b1 和2 个b2 对称分子轨道。Si 原子在3S3P 轨道上的4 个电子和H 原子1S 轨道上的1 个电子被放在活化空间，即这5 个电子分布在上述9 个分子轨道上，剩下的10 个电子放在5 个闭壳层轨道，包括3 个a1，1 个b1，1 个b2，相当于分子的1-3σ和1π轨道。对于每个基组获得的PEC，核间距都选择在0.06 nm 到1.00 nm 之间。应该指出，分子单点能的计算都是使用有限基组来完成的，这必然产生基组重叠误差(BSSE)。Varandas[18]提出BSSE 可以通过将从头算能量点外推到完备基组(CBS)[19-23]极限来纠正。因此，我们选择CBS 的方法修正从头算能量点。

1.2 基组外推

根据Varandas 提出的基于Dunning 相关一致基组外推电子能量的方案[22]，MRCI 电子能量可以写成：

其中R 为指定空间坐标的三维向量，下标表示能量是用AVXZ 基组计算的，上标CAS 和dc 分别表示完备活性空间能量和动态相关能量。CAS 能量使用Karton 和Martin[21]提出的双点外插方案，将AVQZ 和AV5Z 基组外推至CBS 极限。公式为：

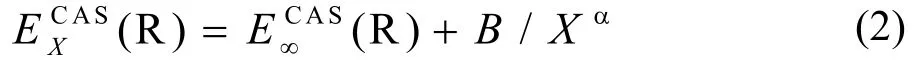
其中B为取决于从头算能量点的参量，α=5.34 为有效的衰变指数，(R)为X→∞的能量。dc 能量为：

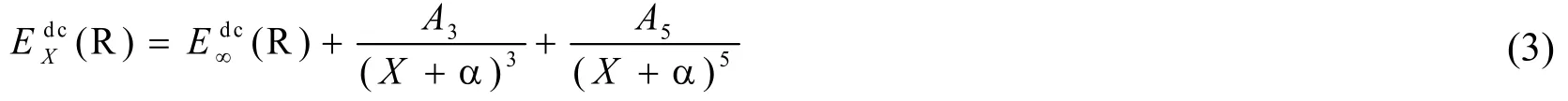
其中A5满足关系：

且A5(0)=0.0037685459Eh，Eh为能量的原子单位，1Eh=27.2116 eV，c=-1.17847713Eh-1/4，α=-3/8，和A3由AVQZ 和AV5Z 基组拟合dc 能量决定。

1.3 解析势能函数(APEFs)

SiH(X2П)APEFs 采用Aguado 和Paniagua[24]提出的函数形式：

Vshort和Vlong分别为短程和长程相互作用的势能，其中：

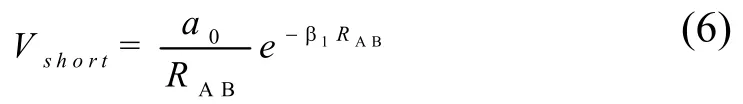
式(6)表明当RAB→0 双原子相互作用势趋近于无穷，式(7)当RAB→∞双原子相互作用势趋于零。

解析势能函数分别通过拟合外插到CBS 极限的数据(使用AVQZ 和AV5Z 的计算数据)和AV6Z的计算数据得到。最后采用最小二乘法拟合程序得出线性参数αi(i=0，1，2，…，n)和非线性参数βi(i=1，2)。

2 结果和讨论

2.1 势能函数

我们分别使用几种不同的基组(AVQZ，AV5Z，AV6Z，USTE(Q，5))，获得SiH(X2П)的能量点，从这些能量点出发，应用(5)式拟合得到APEFs，为了增加精确度，使用了12 个参数，得到了几种不同基组下的APEFs，函数曲线的参数列于表1。

图1 是SiH(X2П)在AV6Z 基组和CBS 方法(使用AV(Q，5)Z 基组)拟合得到的PECs，圆点表示从头算能量点，实线是拟合得到的PECs，从图中可以看出，两种方法得到的PECs 都表现出平滑和收敛的行为，且在AV6Z 和USTE(Q，5)下拟合的PECs 与从头算能量点之间的误差小于5 cm-1，二者之间吻合得非常好。

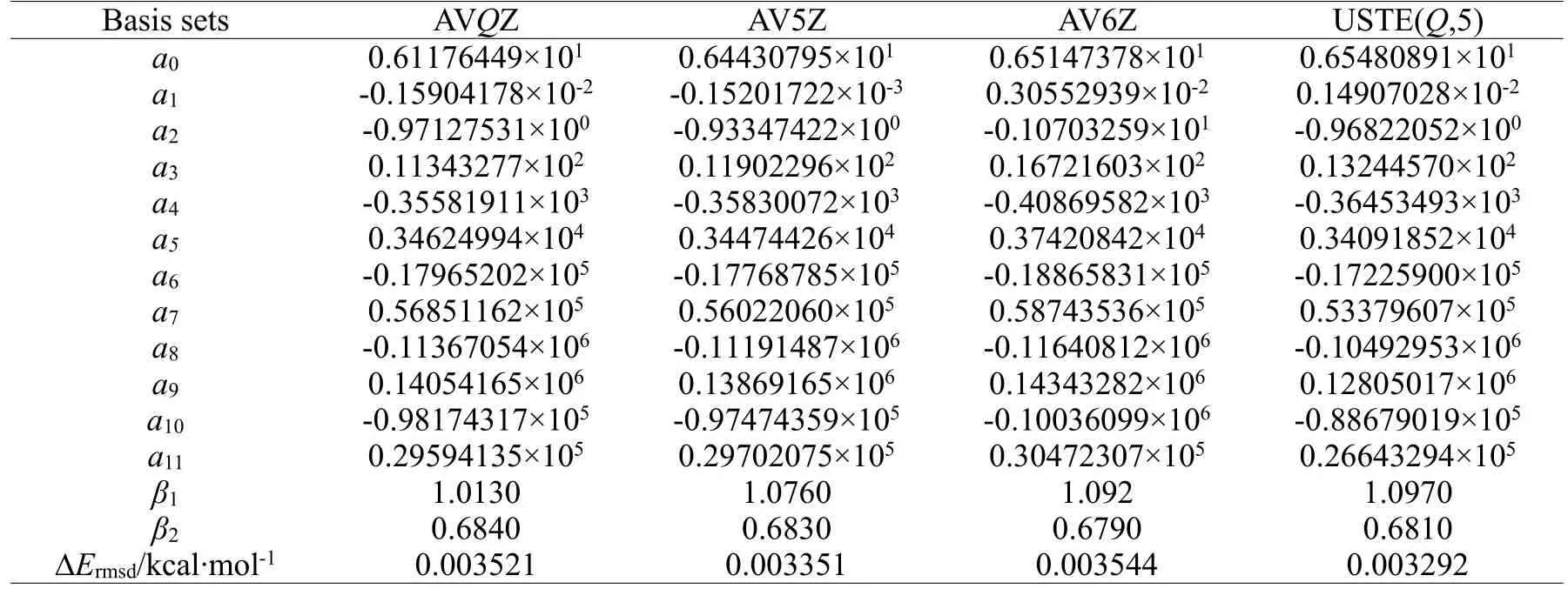
表1 拟合SiH(X2Π)APEFs 的参数Table 1 Fitting the parameters of SiH(X2Π)APEFs

图1 SiH(X2Π)的势能曲线Fig.1 PECs for SiH(X2Π)

为了评估PECs 的拟合质量，可以计算SiH(X2П)在不同基组下的均方根误差(rmsd)，理论公式为：

其中，Vfit(i)和Vab(i)分别是第i个拟合能量和从头算能量，N是拟合能量点的个数，取N=92。ΔErmsd也在表1 中列出。从表中可以发现，对于X2П 态MRCI(Q)/AVQZ，MRCI(Q)/AV5Z，MRCI(Q)/AV6Z 和CBS/USTE(Q，5)的ΔErmsd分别为0.003521 kcal/mol，0.003351 kcal/mol，0.003544 kcal/mol 和0.003292 kcal/mol。使用USTE(Q，5)方法得到的势能函数曲线与从头算能量点之间的误差比使用AV6Z 基组更小，ΔErmsd从0.003544 减小到0.003292 kcal∙mol-1。目前普遍认为AV6Z 是一个耗时量极大的基组，其计算成本远高于AVQZ 和AV5Z。通过使用USTE(Q，5)外推方案，可以在显著降低计算成本的同时得到准确的势能曲线。

2.2 光谱常数

运用拟合MRCI(Q)/AVQZ，MRCI(Q)/AV5Z，MRCI(Q)/AV6Z 和CBS/USTE(Q，5)势能曲线获得的APEFs，计算出SiH(X2П)的光谱常数，以及其他一些高质量的理论和实验研究结果都列在表2中。其中，前四行为不同基组计算的结果，第5，6 行为实验结果[25，26]。7～12 行依次是一些其他文献计算结果[12，16，27-30]。如Cade[12]等人通过求解H-F-R 方程的数值解得到了平衡键长Re，解离能De和αe。但与实验值相比，他们的振动频率ωe过大，解离能De、αe、ωeχe则偏小。总体来看，若以实验数据为参考，Kalemos 等人的理论计算结果[29]是最精确的。另外，从表中前四行可以看出，De随基组从AVQZ 到AV6Z 是单调增加的，其最大值是由CBS/USTE(Q，5)APEF 获得，与AV6Z APEF 获得的De差值为0.00796 eV。由CBS/USTE(Q，5)APEF 计算出的Re为1.5221a0，比两个实验值长0.0020a0和0.0024a0，比Kalemos 等人获得的最新值仅相差0.0002a0，显示出较高精度。CBS/USTE(Q，5)APEF 计算的ωe为2043.26 cm-1，这与实验[26]和理论[29]值分别相差0.74 cm-1和0.11 cm-1。CBS/USTE(Q，5)APEF 计算的光谱常数βe小于实验值，这是因为βe与Re成反比。另外，光谱常数αe与实验[26]和理论[29]值也吻合得非常好，然而，CBS/USTE(Q，5)APEF 计算的ωeχe却和实验值偏差较大，这是因为ωeχe受βe，ωe和力常数(二次方f2，立方f3和四次方f4)的影响，所有这些因素都可能导致ωeχe的值大于实验值。

表2 SiH(X2П)双原子平衡键长Re，解离能De，振动频率ωe，光谱常数ωeχe，αe，βeTable 2 Diatomic equilibrium bond length Re,dissociation energy De,vibrational frequency ωe,and other spectral constant ωeχe,αe,βeof SiH(X2 П)

2.3 振动能级

核运动的径向薛定谔方程为：

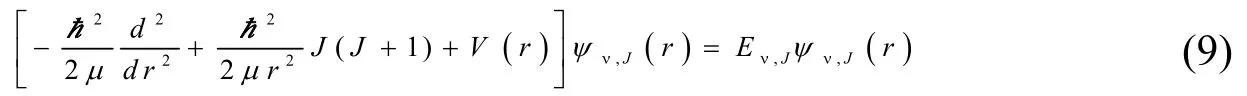
其中ψν，J（r）和Eν，J分别是的本征函数和本征值，V(r)是APEF 的能量，r是双原子SiH 的核间距，μ是分子的约化质量，v和J分别是振动量子数和转动量子数。对于给定的振动能级，转动能级可以写成：

其中G(v)是振动能级，Bv是转动常数，Dv，Hv，Lv，Mv，Nv和Ov是离心畸变常数。

方程(9)可以通过Level7.5 程序包求解，通过解方程可以获得SiH(X2П)的振动能级。进而得到当转动量子数J=0 时的SiH(X2П)的振动态。表3 列出了前21 个振动态的结果。对于每个振动态，获得了G(v)及其经典拐点，一个转动常数Bv和六个离心畸变常数Dv，Hv，Lv，Mv，Nv和Ov。

表3 SiH(X2П)当J=0 时的21 个振动能级G(v)(cm-1)，经典拐点和转动常数Bv(cm-1)Table 3 21 vibration levels G(v)(cm-1),classical turning point and rotation constants Bv(cm-1)of SiH(X2П)when J=0

表3 给出了由CBS/ USTE(Q，5)和AV6Z APEFs 计算的SiH振动能级G(v)，经典拐点及其转动常数Bv。当v=0 时，两种方法计算得到的G(v)差值仅为0.814 cm-1，随着振动量子数v的增加，差值变大，当v=20 时，最大差值为59.470 cm-1。在v=20 处发现Bv的最大差值，其值为2.60×10-2cm-1。此外，经典拐点差值在10-3a0的幅度内，两种方法计算结果表现出一致性。图2 是根据表3 CBS/USTE(Q，5)数据画出的SiH(X2П)振动能级图。

基于CBS/USTE(Q，5)计算的转动量子数J=0 时SiH(X2∏)前21 个振动态的结果列于表4 中。由于目前没有发现关于SiH(X2∏)振动能级、经典拐点、转动常数和离心畸变常数的实验或其他理论工作报告。因此，这些理论数据没有可以比较的对象。但是，根据高质量拟合的APEFs，以及目前计算的光谱参数与其他文献结果的一致性[12，16，25-30]，我们认为表3 和表4 中收集的结果是可靠的。

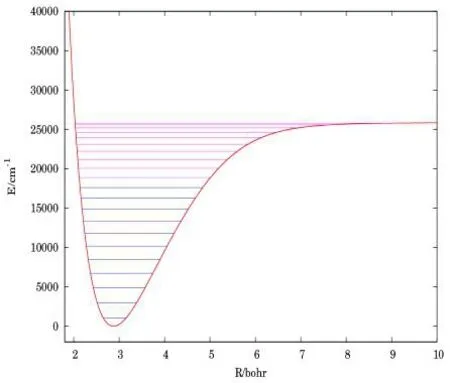
图2 SiH(X2П)振动能级图Fig.2 Vibration energy level of SiH(X2П)

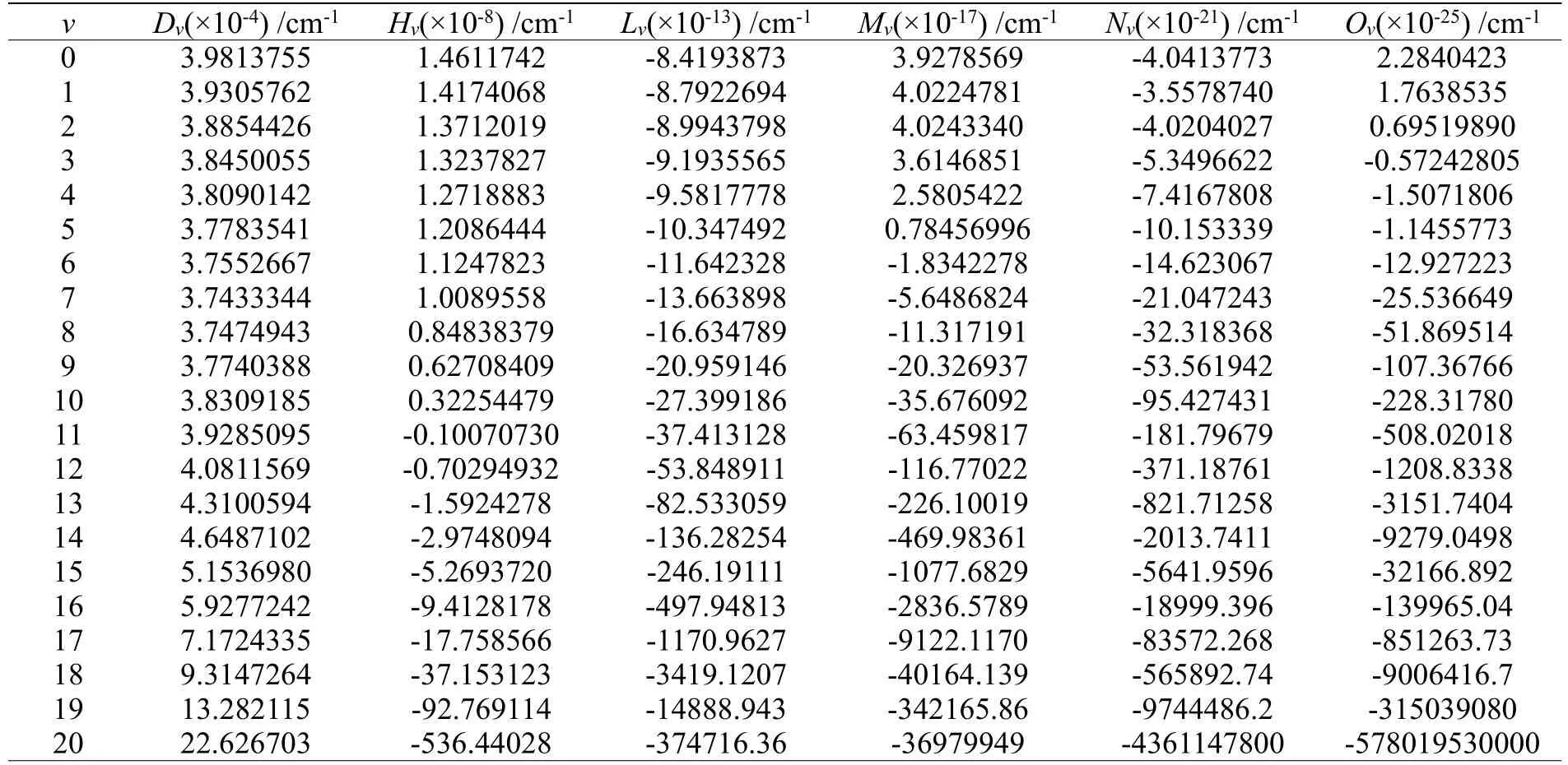
表4 由CBS/USTE(Q,5)APEFs 计算的SiH(X2П)(J=0)的21 个离心畸变常数(cm-1)Table 4 21centrifugal distortion constants(cm-1)of SiH(X2П)(J=0) calculated by CBS/USTE(Q,5)APEFs

3 结论

基于MRCI(Q)方法和aug-cc-pVXZ(AVXZ)和aug-cc-pV(X+d)Z(AVXdZ) (X=Q，5，6)基组，得到了SiH(X2П)从头算能量点，然后采用USTE(Q，5)方案将势能曲线能量点外推到CBS 极限。通过能量点拟合获得APEFs。基于APEFs 我们用不同方法计算了光谱常数De，Re，ωe，Be，αe和ωeχe。通过与已有的实验值和其他理论结果相比较，发现用CBS/USTE(Q，5)和CBS/USTE(Q，5)APEFs 计算的结果精度更高。最后，通过CBS/USTE(Q，5)和CBS/USTE(Q，5)APEFs 求解径向薛定谔方程，首次计算出SiH(X2П)(J=0)的振动态，画出了振动能级图。综上所述，本文的结果提供了SiH(X2П)更准确的光谱参数和更完备的振动态信息。