含非线性阻尼二维Navier-Stokes方程的全局吸引子维数估计

刘文婧，姜金平，李 晨，熊坤翠，李 强

(延安大学数学与计算机科学学院，陕西延安716000)

全局吸引子的结构是比较复杂的，而维数的概念是研究几何性质的重要特征量，故很多学者致力于全局吸引子维数理论的研究。文献[1]证明了无界域上的二维Navier-Stokes方程的存在性并进行维数估计；2000年赵春山在文献[2]中研究了无界域上含线性阻尼的N-S方程的全局吸引子的存在性及维数估计；2015年姜金平在文献[3]中研究了无界域上的含线性阻尼的二维g-N-S方程的全局吸引子的维数估计问题；文献[4]中曹伯芳证明了带非线性阻尼的二维N-S方程的指数吸引子的存在性，由于全局吸引子包含在指数吸引子之中[5]，所以全局吸引子必存在。本文在文献[4]的基础上，研究了带有非线性阻尼项的二维N-S方程的全局吸引子维数估计问题。

本文讨论下面二维Navier-Stokes方程：

(1)

这里的Ω表示R2中具有光滑边界∂Ω的有界区域，u=u(x,t)∈R2和P(x,t)∈R表示速度和压力，μ>0，c|u|βu为阻尼项，β≥0，c>0是两个常数。

1 预备知识

本文中我们记

H上的内积为(u,v)=ʃu·vdx,∀u,v∈H，

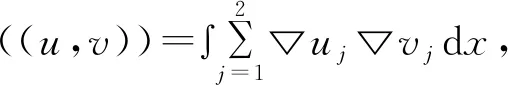
∀u,v∈V，

若u(x,t)是方程(1)的一个光滑解，对(1)中第一式在Ω上用v做内积得：

=(f,v)，

(1.1)

其中B(u)=B(u,u);〈B(u),v〉=b(u,u,v)。

其中B：V×V→V*，V*是V的对偶空间。

定义一个线性stokes算子A：V→V*，(Au,v)=

((u,v))，v∈V且Au=-p△u，其中p是从(L2(Ω))2到H上的投影，令G(u)=Pc|u|βu改写(1)所对应的方程为：

(1.2)

u|t=τ=uτ,τ∈R。

(1.1)等价于V*中如下算子形式：

∀t>0，

(1.3)

假设Poincare不等式成立：

引理1.1 (Gronwall’s Inequality)令x(t)∈满足不等式

x(t)≤x(0)exp[G(t)]+

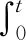
引理1.2 (Young’s Inequality)如果a,b≥0，p,q>1,p-1+q-1=1，

引理1.3 解半群s(t)满足(1.2)，则半群s(t)在v中存在指数引子A′。此引理按文献[4]的满足条件c的方法给出证明，这里从略。

由于全局吸引子包含在指数吸引子之中，所以全局吸引子A存在。

下面给出方程(1.2)解的先验估计[6]，两边与u做内积

(1.4)

其中λ1是-P△的第一特征值，所以

(1.5)

(1.6)

应用引理1.1得

|u(t)|2≤|u0|2e-μλ1t+

(1.7)

取β=min(μλ1,2μ)则

(1.8)

2 全局吸引子的维数估计

下面我们对A的Hausdorff和Fractal维数进行估计∀u0∈A，方程(1.3)在u(t)=s(t)u0的线性化方程为

v(0)=φ，

(2.1)

对∀Ψ∈H，易知方程(2.1)存在唯一解。

v(x,t)∈L∞(τ,T;H)∩L2(τ,T;v),∀T>0，为方便起见，记

F′(u)v=-μAu-c|u|βv-B(u,v)-B(v,u)，

则(2.1)简记为

v(0)=φ，

(2.2)

∀φ1，…φm∈H线性无关，方程(2.2)以v(0)=φi(i=1，…，m)为初值的解记vi(t)(i=1，…，m)，φi(i=1，…，m)为span{v1(t)，…，vm(t)}中的一组标准正交基，Qm(t):H→span(φ1(t)，…，φm(t)}为正交投影算子，记

(2.3)

引理2.1[6]设A为方程(1)的全局吸引子，且存在N>0，使得qN<0，则A的Hausdorff维数为dH(A)≤N，其Fractal维数满足

(2.4)

下面我们估计Tr(F′(u(τ)·Qm(τ)))：

Tr(F′(u(τ)·Qm(τ)))=

B(φ,u),φi〉=

(|φi|=1)，

(2.5)

(2.6)

由Lieb-Thirring不等式[7]

故Tr(F′(u(τ)·Qm(τ)))≤

由(1.5)得

所以

定理2.1 半群{S(t)}t≥0的全局吸引子的Hausdorff及Fractal维数估计如下：