时变时滞T-S模糊模型的稳定性分析

毛晨斐，李江荣，李 琳

(延安大学数学与计算机科学学院，陕西延安716000)

T-S模糊模型是我们所熟知的模糊模型之一，其常用在航天航空及船舶控制等领域，T-S模糊模型运用模糊语句实现非线性系统的局部模型线性化，再通过隶属度函数整合众多局部模型变为全局模糊模型，从而可以使用众多的线性系统知识处理非线性系统的问题，为人们解决非线性系统相关问题另辟蹊径。在实际系统里，经常不可避免的存在一些时滞现象，并且时滞系统的时滞参数自由变化，而这一现象正是造成系统震荡和性能恶化的原因所在。基于上文所述，研究时滞T-S模糊模型的稳定性具有十分重要的意义和价值。这些年国内外研究人员针对具有时滞的非线性系统进行了大量的研究与工作，并且取得了众多研究成果。文献[1]通过构造适当的非二次L-K泛函，再结合隶属函数，给出一则保守型比较低的稳定性条件。文献[2]通过运用Wirtinger积分不等式知识进一步降低了判据的保守性。文献[3]通过设计L-K泛函，并运用贝塞尔不等式提出一个稳定性判据。文献[4]利用时滞划分方法研究了系统的稳定性。针对带有时变时滞的T-S系统，本文设计了一个L-K泛函，然后加入一个积分项并结合文献[5]里的引理2去处理求导所产生的积分部分，最后以数值例子证明了本文所提方法的可行性。

1 系统描述

研究具有如下模糊规则的T-S模糊模型：

Ri：如果k1(t)为Mi1并且…并且kc(t)为Mic，

(1)

其中，x(t)∈Rn表示系统的状态向量，x(t)=φ(t)表示初始状态，Ai,Adi均表示系统矩阵；Miλ(i=1…r;λ=1…c)表示模糊集，r表示模糊规则数，c表示前件变量的维数；h(t)表示时变时滞项，其满足0≤h(t)≤h,h(t)≤d2，h与d2均是已知标量。

当该系统经过模糊融合，可得如下形式：

(2)

在上式中，πt(k(t))表示经过标准化后的隶属度函数，并且有

k(t)=[k1(t)…kc(t)]T，

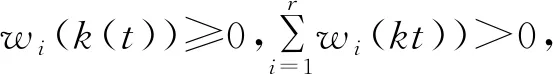
引理1[5]假设存在一个正定矩阵R∈Rn和可导函数x(t)∈[c,d]→Rn，那么下式成立：

(3)

其中p=x(d)-x(c)。

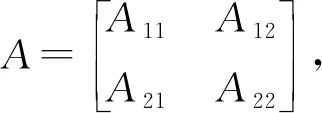
(2)A<0；

2 相关结论

此部分将对(2)式所示系统进行稳定性分析，并且以LMI形式给出稳定性判断条件，为了方便处理L-K函数求导所产生的积分部分，在此定义如下不等式：

(4)

h2R>0

(5)

(6)

其中：

证明设计如下所示的L-K泛函：

V(t)=V1(t)+V2(t)+V3(t)

(7)

V1(t)=xT(t)Px(t)

(8)

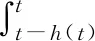
(9)

(10)

现对V(t)进行求导可得：

(11)

(12)

(13)

(1-d2)xT(t-h(t))Qx(t-h(t))

(14)

现将(4)式加入到(13)式中，再结合引理1可得下式：

R[x(t)-x(t-h(t))]

(15)

将(2)式代入到(11)与(15)式里，再令

G=xT(t)Qx(t)-

(1-d2)xT(t-h(t))Qx(t-h(t))-

[x(t)-x(t-h(t))]TR[x(t)-x(t-h(t))]+

xT(t)2P(Aix(t)+Adix(t-h(t)))，

Z=h2R，

结合上述不等式，那么稳定性问题转化为要求下式成立：

(16)

运用引理2并令αT(t)=[xT(t)xT(t-h(t))]，上式要求可转化为下式成立：

αT(t)μiα(t)<0

(17)

综上所述，若式(5)与式(6)均成立，那么式(2)所描述的系统是渐进稳定的，证明完成。

注1：本文在处理由L-K函数求导所产生的积分部分时，引入了一个如(4)式所示的积分项，该式正确的处理了积分不等式的界限问题。文献[7]在处理积分不等式界限问题时运用了错误的方法，若时滞为常数，则此文所述方法是有效的。

注2：相比于文献[8，9]，定理1未引入过多自由权矩阵，可以进一步简化运算难度，提升运算效率。

3 数值例子

例1 考虑下面所示的时滞T-S模糊系统：

R1：如果k1(x(t))为M11，那么

R2：如果k2(x(t))为M21，那么

上述规则的隶属函数依次为：

π2(x(t))=1-π1(x(t))，

通过运用MATLAB里的LMI工具箱，可求出当d2=0.1时时滞上界h的值，并与文献[8]和文献[9，10]所述方法进行对比，结果如表1所示。

表1 d2=0.1时h对应的最大允许时滞上界

通过表1可以得出：定理1所给出的判据相比于文献[8,9]具有更大的时滞上界和更小的保守性，证明了定理1的优越性与可行性。文献[9]中的N表示Legendre不等式的阶数。

4 结论

文章针对带有时变时滞的T-S模糊模型，首先设计了适当的L-K泛函，然后给出一个积分不等式用于处理L-K泛函求导所产生的积分部分，最后以LMI的形式提出一则保守性比较小、决策变量比较少的系统稳定条件，并且用数值例子分析了本文所述方法的优越性与可行性。对实际系统而言，往往存在系统前件变量未知的这种情况，因此前件变量未知系统的输出反馈控制是下一步研究的首要任务。