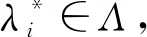广义Iε类凸半无限规划的最优性

苏紫洋，王荣波

(延安大学数学与计算机科学学院，陕西延安716000)

考虑下列半无限规划问题(SIP)

minf(x)，

s.t.g(x,u)≤0,x∈X0⊂Rn,u∈U。

其中f:X0→R是局部Lipschitz函数，g:X0×U→R对于∀u∈U关于x是局部Lipschitz函数，U∈Rm是一个无限参数集，

记:X={x∈X0|g(x,ui)≤0,ui∈U⊆Rm}。

I(x*)={i|g(x*,ui)=0，x*∈X0,ui∈U},

Λ={λi|λi≥0,i∈△，且仅有有限个λi≠0}。

设U*={ui∈U|g(x,ui)≤0,x∈X0,i∈△,△是的任意可数子集}是U的任意可数子集。

△={i|g(x,ui)≤0,x∈X0,ui∈U}。

对于凸函数凸性和广义凸性的研究近年来一直是一个热点话题，凸函数在许多领域扮演着重要的角色，如最优化理论、经济和工程等方面。文献[1,2]将文献[3]引入的Ⅰ类和Ⅱ类不变凸函数进行了进一步推广和应用。文献[4]利用Minch[5]对称梯度的概念，提出了Is类凸，拟Is类凸，伪Is类凸，拟伪Is类凸和伪拟Is类凸的概念，同时在这些广义凸性的条件下得到了一类半无限规划的最优性条件。本文受文献[4]的启迪，利用Clarke广义梯度，定义了Is,c类凸、拟Is,c类凸、伪Is,c类凸、拟伪Is,c类凸等广义凸函数，并且通过讨论研究得到了若干个相对应的最优性理论结果。

1 主要定义

定义1[6]对于在x处满足局部Lipschitz条件的函数f.Clarke定义了在x0∈Rn沿方向d∈Rn的广义方向导数和广义梯度:

∂f(x)={Y∈Rn|〈Y,d〉≤f0(x;d),∀d∈Rn}。

定义2 若对∀x∈X0，∀ε,εi>0，存在正实数函数α，βi:X0×X0→R+/{0}及向量函数η:X0×X0→Rn，使得:

f(x)-f(x0)≥α(x,x0)η(x,x0)Tξ+ε，

∀ξ∈∂f(x)；

-g(x0,ui)≥βi(x,x0)η(x,x0)Tζi+εi，

∀ζi∈∂g(x0,uj)。

则称(f,g)在x0∈X0处是Is,c类凸的，若(f,g)在X0中的任意一点都是Is,c类凸的，则称(f,g)在X0上是Is,c类凸的。当x≠x0时，第一个不等式是严格不等式，则称(f,g)在x0∈X0处或在X0上是半严格Is,c类凸的。

定义3 若对∀x∈X0，∀ε,εi>0及λi∈Λ存在正实数函数α,βi:X0×X0→R+/{0}及向量函数

η:X0×X0→Rn，使得:

α(x,x0)(f(x)-f(x0))≤0⟹

η(x,x0)Tξ+ε≤0,∀ξ∈∂f(x);

则称(f,g)在x0∈X0处是拟Is,c类凸的，若(f,g)在X0中的任意一点都是拟Is,c类凸的，则称(f,g)在x0∈X0上是拟Is,c类凸的。当x≠x0时，第一个公式中的第二个不等式是严格的，则称(f,g)在x0∈X0处或在X0上是半严格拟Is,c类凸的。

定义4 若对∀x∈X0，∀ε,εi>0及λi∈Λ存在正实数函数α，βi:X0×X0→R+/{0}及向量函数η:X0×X0→Rn，使得:

η(x,x0)Tξ+ε≥0⟹

α(x,x0)(f(x)-f(x0))≥0,∀ξ∈∂f(x)；

则称(f,g)在x0∈X0处是伪Is,c类凸的，若(f,g)在X0中的任意一点都是伪Is,c类凸的，则称(f,g)在X0上是伪Is,c类凸的。当x≠x0时，第二个公式中的第二个不等式是严格的，则称(f,g)在x0∈X0处或在X0上是半严格伪Is,c类凸的。

定义5 若对∀x∈X0,∀ε,εi>0及λi∈Λ存在正实数函数α,βi:X0×X0→R+/{0}及向量函数η:X0×X0→Rn，使得：

α(x,x0)(f(x)-f(x0))≤0⟹

η(x,x0)Tξ+ε≤0，∀ξ∈∂f(x)；

则称(f,g)在x0∈X0处是拟伪Is,c类凸的，若(f,g)在X0中的任意一点都是拟伪Is,c类凸的，则称(f,g)在X0上是拟伪Is,c类凸的。当x≠x0时，第二个公式中的第二个不等式是严格的，则称(f,g)在x0∈X0处或在上是半严格拟伪Is,c类凸的。

定义6 若对∀x∈X0，∀ε,εi>0及λi∈Λ存在正实数函数α,βi:X0×X0→R+/{0}及向量函数η:X0×X0，使得：

η(x,x0)Tξ+ε≥0⟹

α(x,x0)(f(x)-f(x0))≥0，∀ξ∈∂f(x)；

则称(f,g)在x0∈X0处是伪拟Is,c类凸的，若(f,g)在X中的任意一点都是伪拟Is,c类凸的，则称(f,g)在X0上是伪拟Is,c类凸的。当x≠x0时，第一个公式中的第二个不等式是严格的，则称(f,g)在x0∈X0处或在X0上是半严格伪拟Is,c类凸的。

2 最优性条件

定理1 假设x0∈X0，如果

(b)对于函数α>0，βi>0，f(g)在X上为Is,c类凸的(或者半严格Is,c类凸的)。

则x0为规划(SIP)的最优解。

证明根据条件(b)可得，对∀x∈X0，∀ε,εi>0及存在正实数函数α,βi:X0×X0→R+/{0}及向量函数η:X0×X0，使得:

f(x)-f(x0)≥α(x,x0)η(x,x0)Tξ+ε，

∀ξ∈∂f(x)。

-g(x0,ui)≥βi(x,x0)η(x,x0)Tζi+εi，

∀ζi∈∂g(x0,ui)。

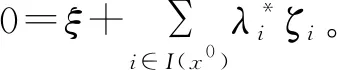
(1)

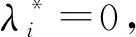
(2)

由(1)式和(2)式可得

(3)

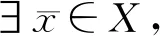
这与(3)式矛盾，所以x0是规划(SIP)的最优解。

定理2 假设x0∈X0，如果

(b)对于函数α>0，βi>0，f(g)在X上为拟Is,c类凸的(或者半严格拟Is,c类凸的)。

则x0为规划(SIP)的最优解。

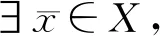
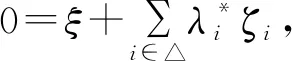
(4)

定理3 假设x0∈X0，如果

(b)对于函数α>0，βi>0，(f,g)在X上为半严格伪Is,c类凸的。

则x0为规划(SIP)的最优解。

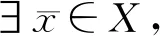
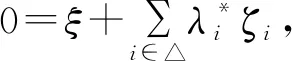
(5)

定理4 假设x0∈X0，如果

(b)对于函数α>0，βi>0，(f,g)在X上为半严格拟伪Is,c类凸的。

则x0为规划(SIP)的最优解。

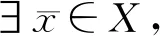
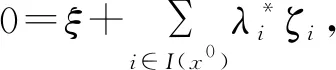
(6)

定理5 假设x0∈X0，如果

(b)对于函数α>0，βi>0，(f,g)在X上为伪拟Is,c类凸的(或者半严格伪拟Is,c类凸)。

则x0为规划(SIP)的最优解。

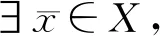
(7)

另一方面，当i∈I(x0)时，g(x0,ui)=0；当i∉

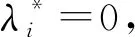
(8)

将(7)式和(8)式相加可得

(9)

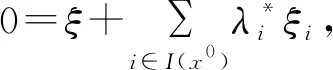
所以(9)等价于