四元欧拉函数方程φ(abcd)=φ(a)+φ(b)+2[φ(c)+φ(d)]的正整数解

梁晓艳，高 丽，高 倩

(延安大学数学与计算机科学学院，陕西延安716000)

对于任意正整数n，欧拉函数φ(n)表示1，2，3，…n-1中与n互素的正整数的个数。欧拉函数在数论中有着重要的作用，近年来，有关欧拉函数的性质以及欧拉方程吸引了很多学者的研究兴趣[1-4]。文献[5-7]研究了二元、三元欧拉函数方程的正整数解；文献[8]研究了四元欧拉函数方程的正整数解。本文在此基础上，利用初等数论的相关知识，研究了四元欧拉函数方程φ(abcd)=φ(a)+φ(b)+2[φ(c)+φ(d)]的正整数解问题。

1 相关引理

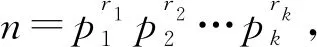
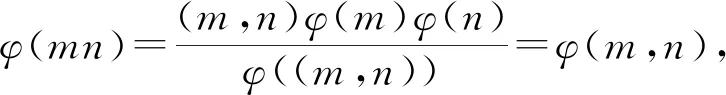
引理3[3]当n≥2时，有φ(n)

引理4[3]设n为正整数，p为素数，则

2 定理及证明

定理四元欧拉函数方程φ(abcd)=φ(a)+

φ(b)+2[φ(c)+φ(d)]的正整数解为：

(a,b,c,d)=(2,1,2,4),(2,2,1,4),(1,2,2,4),(2,1,2,6),(2,2,1,6),(1,2,2,6),(1,1,3,9),(1,1,3,18),(1,2,4,2),(2,1,4,2),(2,2,5,1),(2,2,4,1),(3,7,1,1),(3,12,1,1),(1,1,9,3),(1,1,18,3)。

证明对于欧拉函数方程

φ(abcd)=φ(a)+φ(b)+2[φ(c)+φ(d)]，

由引理得

φ(a)φ(b)φ(c)φ(d)，

即φ(abcd)=φ(a)+φ(b)+2[φ(c)+φ(d)]

≥φ(a)φ(b)φ(c)φ(d)，

φ(a)+φ(b)+2φ(c)≥

φ(d)[φ(a)φ(b)φ(c)-2]。

根据φ(a)φ(b)φ(c)进行分情况讨论：

情况1φ(a)φ(b)φ(c)≤2，即

φ(a)φ(b)φ(c)=1,2；

1.1 当φ(a)φ(b)φ(c)=1时，有

φ(a)=φ(b)=φ(c)=1，a=b=c=1,2，

即φ(abcd)=4+2φ(d)，

经检验，有解

(a,b,c,d)=(2,1,2,4),(2,2,1,4),(1,2,2,4),(2,1,2,6),(2,2,1,6),(1,2,2,6)。

1.2 当φ(a)φ(b)φ(c)=2时，有φ(a)=φ(b)=1,φ(c)=2或φ(a)=φ(c)=1,φ(b)=2或φ(b)=φ(c)=1,φ(a)=2。

A:φ(a)=φ(b)=1,φ(c)=2,

a=b=1,2,c=3,4,6，

φ(abcd)=φ(a)+φ(b)+2[φ(c)+φ(d)]=

6+2φ(d)，

经检验，有解

(a，b，c，d)=(1,1,3,9),(1,1,3,18),(1,2,4,2),(2,1,4,2)。

B:φ(a)=φ(c)=1,φ(b)=2,

a=c=1,2,b=3,4,6,

φ(abcd)=φ(a)+φ(b)+2[φ(c)+φ(d)]=

5+2φ(d)，

由引理3知，方程无解。

C:φ(b)=φ(c)=1,φ(a)=2,

b=c=1,2,a=3,4,6,

φ(abcd=φ(a)+φ(b)+2[φ(c)+φ(d)]=

5+2φ(d)，

由引理3知，方程无解。

情况2φ(a)φ(b)φ(c)>2时，

(φ(a)-1)(φ(b)-1)(φ(c)-1)≥0，即

φ(a)φ(b)φ(c)-φ(a)φ(b)-φ(b)φ(c)-

φ(a)φ(c)+φ(a)+φ(b)+φ(c)-1≥0，

φ(a)φ(b)φ(c)-1≥

φ(a)φ(b)+φ(b)φ(c)+φ(a)φ(c)-

(φ(a)+φ(b)+φ(c))。

(1)

由(φ(a)-1)(φ(b)-1)≥0

得φ(a)φ(b)≥φ(a)+φ(b)-1。

(2)

同理得φ(b)φ(c)≥φ(b)+φ(c)-1，

φ(a)φ(c)≥φ(a)+φ(c)-1，整理得

φ(a)φ(b)+φ(b)φ(c)+φ(a)φ(c)≥

2[φ(a)+φ(b)+φ(c)]-3。

(3)

由(1)+(3)得φ(a)φ(b)φ(c)+2≥

φ(a)+φ(b)+φ(c)。

由φ(a)+φ(b)+2φ(c)≥

φ(d)[φ(a)φ(b)φ(c)-2]，

所以φ(d)=1,2,4,6,8。

2.1 当φ(d)=1时，

φ(abcd)=φ(a)+φ(b)+2φ(c)+2≥

φ(a)φ(b)φ(c)，

即φ(a)+φ(b)+2≥φ(c)[φ(a)φ(b)-2]。

2.1.1 当φ(a)φ(b)≤2时，有

φ(a)φ(b)=1,2。

A:当φ(a)φ(b)=1时，φ(a)=φ(b)=1，则φ(abcd)=1+1+2[φ(c)+1]=4+2φ(c)，经检验，有解(a,b,c,d)=(2,2,4,1),(2,2,5,1)。

B:当φ(a)φ(b)=2时，取φ(a)=1,φ(b)=2和φ(a)=2,φ(b)=1,φ(abcd)=5+2φ(c),由引理3知，方程无解。

2.1.2 当φ(a)φ(b)>2时，

所以φ(c)=1,2,4,6。

A:当φ(c)=1时，

φ(abcd)=φ(a)+φ(b)+4=

4+φ(a)+φ(b)≥φ(a)φ(b)，解得

即φ(a)=1,2,4,6。

取φ(a)=1时，

φ(abcd)=1+φ(b)+4=5+φ(b)，

由引理3知，方程无解。

取φ(a)=2时，

φ(abcd)=2+φ(b)+4=6+φ(b)，

a=3,4,6，c=d=1,2,

经检验，有解

(a,b,c,d)=(3,7,1,1),(3,12,1,1)。

取φ(a)=4时，

φ(abcd)=4+φ(b)+4=8+φ(b)，

a=5,8,10,12,c=d=1,2，

经检验，方程无解。

取φ(a)=6时，

φ(abcd)=6+φ(b)+4=10+φ(b)≥6φ(b)，

解得φ(b)=1,2，a=7,9,14,18,c=d=1,2，

经检验，方程无解。

B:当φ(c)=2时，

φ(abcd)=φ(a)+φ(b)+6≥2φ(a)φ(b)，

由引理知，φ(a)+6≥2φ(a)-1，

解得φ(a)≤7，即φ(a)=1,2,4,6。

取φ(a)=1时，

φ(abcd)=1+φ(b)+6=7+φ(b)，

由引理3知，方程无解。

取φ(a)=2时，

φ(abcd)=2+φ(b)+6=8+φ(b)≥4φ(b)，

解得φ(b)=1,2，由引理知φ(b)=2，经检验，方程无解。

取φ(a)=4时，

φ(abcd)=4+φ(b)+6=10+φ(b)≥8φ(b)，

解得φ(b)=1，代入得φ(abcd)=11，由引理3知，方程无解。

取φ(a)=6时，

φ(abcd)=6+φ(b)+6=12+φ(b)≥12φ(b)，

解得φ(b)=1，代入得φ(abcd)=13，由引理3知，方程无解。

C:当φ(c)=4时，

φ(abcd)=φ(a)+φ(b)+10≥4φ(a)φ(b)，

由引理知，φ(a)+10≥4φ(a)-1，

解得φ(a)≤3，即φ(a)=1,2。

取φ(a)=1时，

φ(abcd)=1+φ(b)+10=11+φ(b)，

由引理3知，方程无解。

取φ(a)=2时，

φ(abcd)=2+φ(b)+10=12+φ(b)≥8φ(b)，

解得φ(b)=1，代入得φ(abcd)=13，由引理3知，方程无解。

D:当φ(c)=6时，

φ(abcd)=φ(a)+φ(b)+14≥6φ(a)φ(b)，

由引理知，φ(a)+14≥6φ(a)-1，

解得φ(a)≤3，即φ(a)=1,2。

取φ(a)=1时，

φ(abcd)=1+φ(b)+14=15+φ(b)，

由引理3知，方程无解。

取φ(a)=2时，

φ(abcd)=2+φ(b)+14=16+φ(b)≥

12φ(b)，

解得φ(b)=1，代入得φ(abcd)=17，由引理3知，方程无解。

2.2 当φ(d)=2时，

φ(abcd)=φ(a)+φ(b)+2[φ(c)+2]≥

2φ(a)φ(b)φ(c)，

即φ(a)+φ(b)+4≥2φ(c)[φ(a)φ(b)-1]。

2.2.1 当φ(a)φ(b)=1时，有

φ(a)=φ(b)=1,

φ(abcd)=1+1+2[φ(c)+2]=6+2φ(c)，

a=b=1,2,d=3,4,6，

经检验有解

(a,b,c,d)=(1,1,9,3),(1,1,18,3),(1,2,2,4),(2,1,2,4)。

2.2.2 当φ(a)φ(b)≥2时，

由引理知，φ(a)φ(b)+5≥2φ(a)φ(b)-1，

解得φ(a)φ(b)≤6，又因为φ(a)φ(b)≥2，所以φ(a)φ(b)=2,4,6。

A:当φ(a)φ(b)=2时，

取φ(a)=1，φ(b)=2，

φ(abcd)=1+2+2[φ(c)+2]=7+2φ(c)，

由引理3知，方程无解。

取φ(a)=2,φ(b)=1,

φ(abcd)=2+1+2[φ(c)+2]=7+2φ(c)，

由引理3知，方程无解。

B:当φ(a)φ(b)=4时，

取φ(a)=1,φ(b)=4，

φ(abcd)=1+4+2[φ(c)+2]=9+2φ(c)，

由引理3知，方程无解。

取φ(a)=4，φ(b)=1，

φ(abcd)=4+1+2[φ(c)+2]=9+2φ(c)，

由引理3知，方程无解。

取φ(a)=2,φ(b)=2,

φ(abcd)=2+2+2[φ(c)+2]≥8φ(c)，

解得φ(c)=1，经检验，方程无解。

C:当φ(a)φ(b)=6时，

取φ(a)=1,φ(b)=6，

φ(abcd)=1+6+2[φ(c)+2]=11+2φ(c)，

由引理3知，方程无解。

取φ(a)=6,φ(b)=1，

φ(abcd)=6+1+2[φ(c)+2]=11+2φ(c)，

由引理3知，方程无解。

2.3 当φ(d)=4时，

φ(abcd)=φ(a)+φ(b)+2[φ(c)+4]≥

4φ(a)φ(b)φ(c)，

即φ(a)+φ(b)+8≥2φ(c)[φ(a)φ(b)-1]。

2.3.1 当φ(a)φ(b)=1时，因为

φ(a)φ(b)φ(c)>2，所以φ(c)>2，所以

φ(abcd)=1+1+2[φ(c)+4]=

10+2φ(c)≥4φ(c)，

解得φ(c)=4，经检验，方程无解。

2.3.2 当φ(a)≥2，可得

由引理知，φ(a)φ(b)+9≥4φ(a)φ(b)-2，

解得φ(a)φ(b)≤3，因为φ(a)≥2,φ(b)≥1，所以φ(a)φ(b)=2。有

φ(a)=2,φ(b)=1，

φ(abcd)=2+1+2[φ(c)+4]=11+2φ(c)，

由引理3知，方程无解。

2.4 当φ(d)=6时，

φ(abcd)=φ(a)+φ(b)+2[φ(c)+6]≥

6φ(a)φ(b)φ(c)，

即φ(a)+φ(b)+12≥

φ(c)[6φ(a)φ(b)-2]。

2.4.1 当φ(a)φ(b)=1时，

φ(abcd)=1+1+2[φ(c)+6]=

14+2φ(c)≥6φ(c)，

解得φ(c)=1,2，因为φ(a)φ(b)φ(c)>2，所以φ(c)>2，即方程无解。

2.4.2 当φ(a)≥2，可得

由引理知，φ(a)φ(b)+13≥6φ(a)φ(b)-2，

解得φ(a)φ(b)≤3，因为φ(a)≥2,φ(b)≥1，所以φ(a)φ(b)=2。有

φ(a)=2，φ(b)=1，

φ(abcd)=2+1+2[φ(c)+6]=15+2φ(c)，

由引理3知，方程无解。

2.5 当φ(d)=8时，

φ(abcd)=φ(a)+φ(b)+2[φ(c)+8]≥

8φ(a)φ(b)φ(c)，

即φ(a)+φ(b)+16≥

φ(c)[8φ(a)φ(b)-2]。

2.5.1 当φ(a)φ(b)=1时，

φ(abcd)=1+1+2[φ(c)+8]=

18+2φ(c)≥8φ(c)，

解得φ(c)=1,2，因为φ(a)φ(b)φ(c)>2，所以φ(c)>2，即方程无解。

2.5.2 当φ(a)≥2，可得

由引理知，φ(a)φ(b)+17≥8φ(a)φ(b)-2，

解得φ(a)φ(b)≤2，因为φ(a)≥2,φ(b)≥1，所以φ(a)φ(b)=2。有

φ(a)=2，φ(b)=1，

φ(abcd)=2+1+2[φ(c)+8]=19+2φ(c)，

由引理3知，方程无解。

综上所述，定理得证。