SPMT悬挂液压系统故障仿真与诊断研究

武汉理工大学物流工程学院 武汉 430063

0 引言

自行式模块运输车（Self-propelled modular transporter，SPMT）是一种应用广泛的多轴载重车辆，其悬挂系统包含众多液压元件，故障现象和故障原因复杂，而液压泵故障是液压系统中常见的故障，因此对悬挂液压系统中液压泵的故障诊断进行研究具有重要意义。

在液压泵的故障诊断研究中，一般采用基于信号处理的方法，从信号中提取故障特征并使用分类识别方法完成诊断。姜万录等用小波变换提取信号的故障特征，并利用基于SVM和证据理论的多数据融合新方法实现液压泵故障诊断[1]。唐宏宾等提出了基于经验模式分解(EMD)和包络谱分析的液压泵故障诊断方法[2]。张捍东等利用粒子群算法优化BP网络实现了对液压泵的故障诊断[3]。Hancock等使用小波包分析分解液压泵的振动信号，并利用自适应神经模糊推理系统对故障进行识别[4]。

对于液压泵的故障诊断，许多研究提出了多种故障特征提取和识别方法，都收到较好的效果。但是这些研究多以单纯的液压泵本身为对象，而在特定的实际液压系统中，液压泵的流量输出特性和故障特性会受到系统中其他因素的影响而产生变化，其故障诊断需要具体研究。

针对SPMT悬挂系统中液压泵的故障诊断，本文首先在AMESim中建立系统模型对故障进行仿真，并从仿真模型中获取丰富的正常工况和故障工况的样本数据。然后提出了小波包分析、主成分分析和支持向量机相结合的方法，对液压泵的故障进行诊断。

1 SPMT悬挂液压系统

以某款6轴SPMT为研究对象，其悬挂系统采用负载敏感技术，通过负载的压力反馈自动调节变量液压泵的排量，使泵源只提供系统需要的的压力和流量，最大程度地提高了系统效率，悬挂液压系统的原理如图1所示。

系统中各液压缸之间由截止阀控制通断，通过控制截止阀的启闭可以改变液压缸的分组，将系统分为多个支路。各液压缸回路上安装有防爆阀，在连接液压缸的软管破裂导致大量泄漏时可以迅速封闭回路，保证悬挂液压系统中其他回路中的压力不受影响。

每个支路中的定差减压阀控制比例换向阀进出油口压差保持恒定，根据节流口流量特性，通过滑阀的流量与负载无关，仅受换向阀的开度控制；受负载敏感阀控制，液压泵的出口压力仅稍高于最高的负载压力，两者之间的压差恒定；压力切断阀或溢流阀限制系统的最高压力，保证系统安全，液压系统的主要参数: 液压泵排量95cm3/r, 负载敏感阀压力3 MPa, 压力切断阀压力35 MPa, 溢流阀压力38 MPa, 定差减压阀压力2 MPa, 单缸负载质量20 t。

悬挂系统工作中常见的故障有油液污染、管路泄漏以及液压泵、液压缸、液压阀等元件的失效故障。其中斜盘式轴向柱塞泵工作时长时间磨损会使泵出现滑靴松动或脱落、柱塞与缸体间的磨损、缸体与配流盘间的磨损等问题，本文主要研究液压泵活塞磨损泄漏的故障诊断。

2 AMESim建模与仿真

2.1 悬挂液压系统建模

AMESim是一款多学科领域对复杂系统建模与仿真的软件，其液压库包含了大量常见的液压元件模型，对于一些复杂的元件，则可以使用液压元件设计库（HCD）自行搭建模型。

斜盘式轴向柱塞泵是通过柱塞的往复运动实现吸油和排油，通过改变斜盘的倾角来改变泵的排量。在AMESim中可以根据柱塞泵的工作原理建立结构模型，并模拟柱塞磨损故障[5]。根据活塞的运动学分析建立如图2所示的单活塞模型。

在活塞模型中设有一个泄漏模型，通过设置泄漏间隙可以模拟液压泵活塞泄漏故障。将活塞模型封装为超级元件，用5个活塞元件组成一个斜盘式轴向柱塞泵模型，见图3，将图中柱塞泵模型封装为超级元件。

悬挂液压系统分为液压缸进油、回油和中位保持三种工况，本文以进油工况的一个支路为研究对象。此时比例换向阀可以简化为一个调速阀，当管路不出现泄漏时防爆阀相当于一个节流口。根据液压原理图分别建立负载敏感阀、压力切断阀、定差减压阀、比例换向阀、柱塞缸等模型，各模块与上述柱塞泵模型组装后得到悬挂液压系统的模型，如图4所示。

2.2 故障仿真

在悬挂液压系统模型中，将液压泵的某个柱塞的泄漏间隙d(单位mm)分别设置为（0，0.05，0.1，0.15，0.2），模拟液压泵不同程度的柱塞泄漏故障。设置电机转速为1 200 r/min，阀口输入信号0.7，采样步长0.002，进行多组仿真，得到液压泵输出流量及其局部放大图，如图5所示。

仿真结果显示，由于系统中负载敏感回路的存在，系统的总流量只受比例换向阀控制，液压泵的柱塞泄漏几乎不影响液压泵的平均输出流量，但会影响流量脉动的频率和幅值。

3 故障诊断方法

3.1 小波包分析

小波变换通过使用一组正交的、能量有限的小波函数作为基函数，将函数分解为一系列基函数的线性组合对原函数进行拟合，小波展开的近似形式为

小波变换将信号分解为低频和高频两部分，只对低频部分进一步分解，而小波包分析[6]则对低频信号和高频信号都做进一步分解，是一种更精细的信号分析方法。在应用小波包分解信号时，选择合适的母小波函数和父小波函数，按照一定的算法通过尺度变换和平移变换生成一组基函数，在不同的分解尺度下可以对信号的频带按照需求做不同程度的划分。

以图5中没有泄漏的流量信号为例，从中截取2 s到4 s的信号作为原始信号，在Matlab中使用Dmeyer小波对信号做4层小波包分解，将信号分解为16个频带的子信号。信号的小波包树图如图6所示，图中(0,0)为原信号,（j，i）表示j层分解尺度下的第i个节点信号。

故障仿真中流量信号的采样频率为500 Hz，根据采样定理，奈奎斯特（Nyquist）采样频率为250 Hz，信号经过4层分解被分解成16个频带，每个频带的长度f0=15.625 Hz，各节点信号对应的频率范围如表1所示。

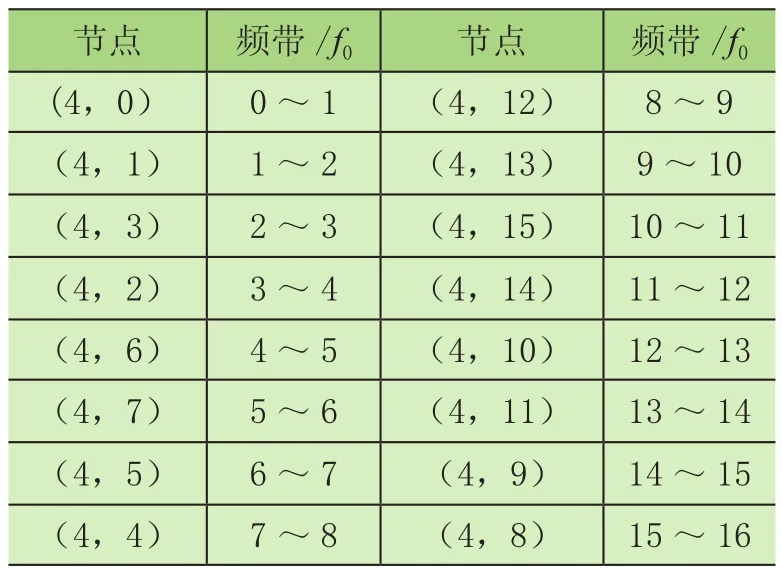
表1 信号频带划分

在小波包分析中，子带能量谱描述了信号的能量在各频带上的分布特征，液压泵柱塞泄漏会引起各频带能量分布的变化，因而可以将信号的子带能量谱作为特征信息对液压泵的故障状态进行诊断。

记第4层的节点信号S4,k(t)的能量为E4,k(k=0，1,…，15），则

式（2）中xk,m为重构信号的离散点幅值，N为信号的离散点个数，为了消除不同阀口开度下流量大小的影响，计算S4,k(t)在整个信号中的能量占比

计算流量信号分解后的所有子带的能量占比，则信号的特征向量T= [p4,0,p4,1,p4,2, … ,p4,15]T。

3.2 主成分分析

主成分分析法[7]（PCA）是一种多元统计方法，通过对原始特征量的线性变化得到一组互不相关的综合特征，称为主成分。在损失很少信息的前提下，使用包含最多原始样本信息的几个主成分来重新表示样本，从而实现对样本的特征进行降维的目的。

对于一组包含n个样本，每个样本有m个特征量的样本数据Am×n，首先对数据进行去中心化得到新的样本矩阵X，有

式中：aij为A中第j个样本的第i个特征值，xij为其在X中对应的去中心化后的值。

计算矩阵X的协方差矩阵

求解C的特征值λi（i=1，2,…,m）和对应的单位特征向量vi，所有的特征向量组成的单位正交基即为主成分。将vi按照λi的降序进行排列构成m维单位正交空间V，则样本在新的正交空间中表示为

在主成分分析中用贡献率表示每个主成分包含的原始数据的信息量，在进行主成分分析时一般要求累计贡献率超过95%[8]。每个主成分对原始信息的贡献率

当前k个主成分的累计贡献率超过95%时，意味着前k个主成分基本包含原数据的全部信息，可以替代原m维特征向量，达到对特征向量降维的目的。

3.3 支持向量机

支持向量机[9]（SVM）理论是一个二分类模型，它通过寻找一个超平面来将两类样本数据进行分割，同时要求样本分割的间隔最大化。对给定的二分类训练样本集D={(x1,y1), (x2,y2), … , (xi,yi)}，yi∈ {-1,1},其中xi是m维的样本数据，yi是每个样本对应的类别，其超平面表示为wx+b=0。

当样本为二维数据时，超平面是一条直线，距离超平面最近的样本点满足wx+b=±1，它们被称为支持向量，如图7所示。

由于实际应用几乎不存在完全线性可分的问题，为每个样本引入一个松弛变量ζi以及总的惩罚参数C。ζi表征该样本不满足约束的程度，而C值则表示对样本分类错误的惩罚程度，超平面（w，b）应满足

式（8）的求解是一个凸二次规划问题，使用拉格朗日乘子法得到其对偶问题，并结合序列最小优化（SMO）算法将SVM 二分类问题的目标函数最终转化为对式（9）的求解，有

式中 ：k(xi,xj)被称为核函数，在样本线性不可分时，支持向量机将训练样本从原始空间映射到一个更高维的空间，使样本在这个空间中线性可分。在求解过程中涉及高维空间中特征向量的内积计算，比较困难，核函数的作用就是将其转换到原始空间计算，常用的核函数有线性核、多项式核、高斯核等。

4 液压泵故障诊断

4.1 特征提取

液压泵的活塞泄漏间隙小于0.05 mm时视为正常，间隙大于等于0.05 mm时判定为故障，在AMESim仿真模型中改变阀口开度信号a、负载大小L（单位t）和故障程度d（单位mm），获取不同的样本数据。

分别取L、a、d为（20，16，12）、（0.2，0.4，0.6，0.8）、（0，0.01，0.02，0.03），得到48个正常样本；分别取L、a、d为（20，16，12）、（0.2，0.4，0.6，0.8）、（0.075，0.1，0.125，0.15，0.175，0.2），得到72个故障样本。

对所有120个样本信号进行小波包分析，并提取子带能量特征向量Ti=[pi1,pi2,pi3,…,pi16]T，得到总样本数据为T16×120=[T1,T2,T3, …，T72]，部分样本的子带能量特征见表2。

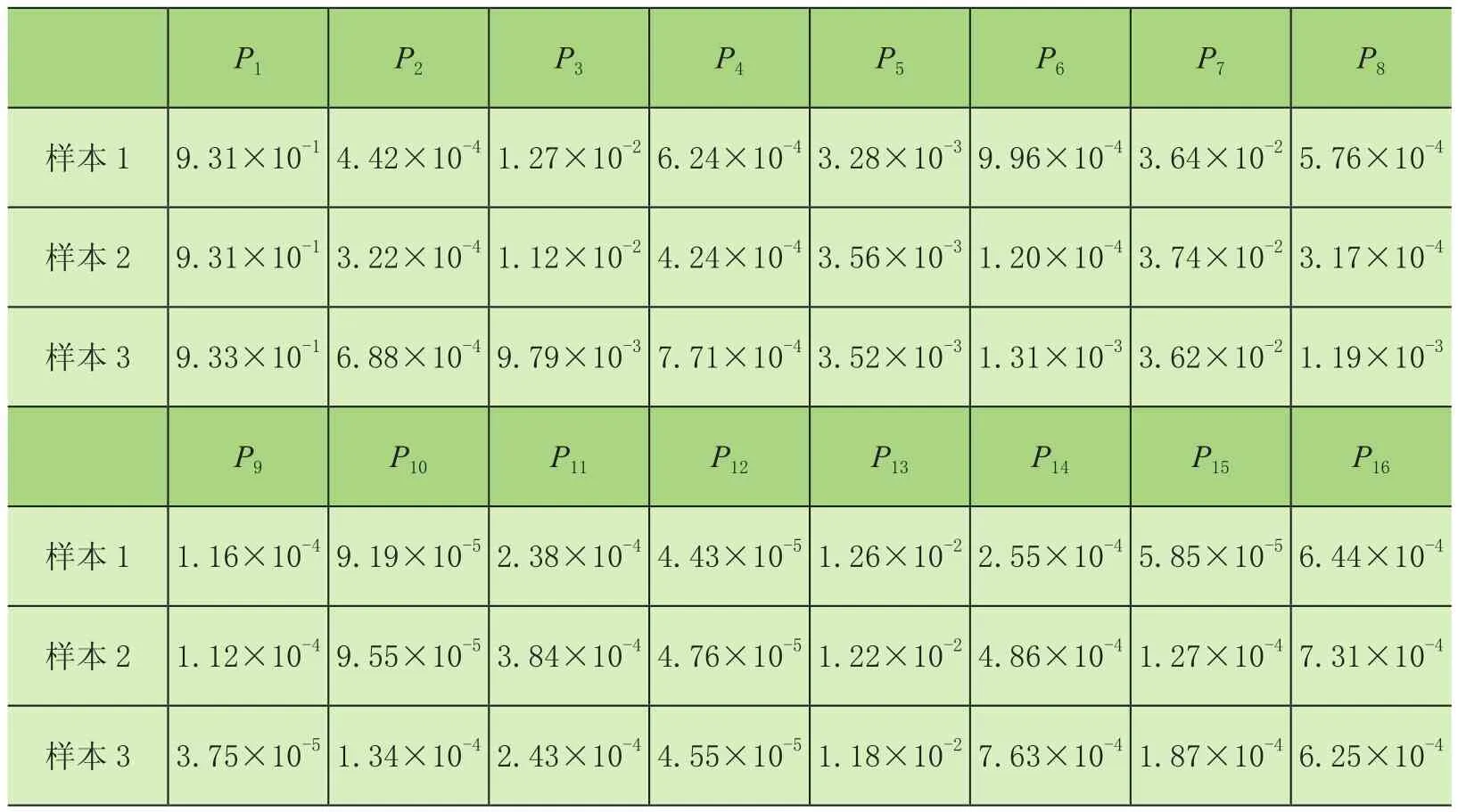
表2 子带能量占比

对上述总样本特征T16×120进行主成分分析，得到主成分以及样本在主成分空间的表示，并计算各主成分的贡献率，按降序排列如表3所示。

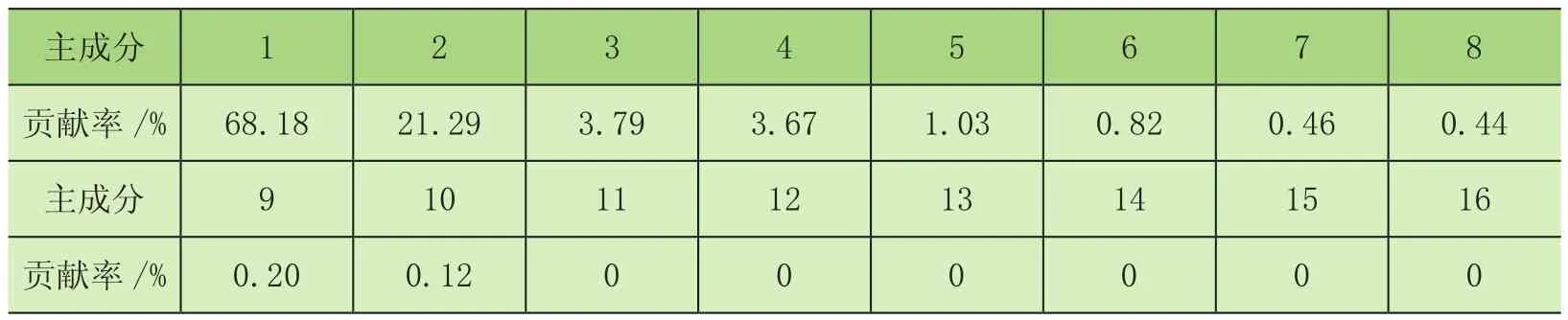
表3 主成分贡献率

前4个主成分的累计贡献率为96.63%，已包含原始样本数据的大部分信息，可以替代原始样本数据。取前四个主成分作为样本新的特征量，总样本记为Z4×120。

4.2 故障识别

在使用支持向量机方法实现故障识别时，核函数的类型和参数会影响SVM的分类效果和泛化能力，本文选择高斯核函数，其计算公式为

高斯核函数将原始样本空间映射成无限维空间，其分类的局部性能优异，式中：σ是函数的宽度参数，决定了函数的径向作用范围。

使用高斯核函数的SVM的两个参数中，σ越小则对样本的划分能力越强，但是太小会导致过拟合；C越大对数据的拟合越好，但同时泛化能力降低。为了选择使SVM性能最好的参数，使用改进的网格搜索法，先在较大范围σ∈[σ1,σ2]，C∈[C1,C2]内等间隔取值，对所有组合进行尝试并选择使SVM性能最好的一组，再以该组参数为中心做更细致的搜索，从而得到最优参数。

从总样本Z中随机选择90个作为SVM的训练样本，用剩下的30个样本测试SVM对样本类别的预测准确率。使用改进的网格搜索法两次搜索中效果最好的参数组合和对应的SVM的预测准确率见表4。

表4 SVM诊断结果

经过两次搜索，最终确定了SVM的参数为σ=2.9，C=2，此时对30个测试样本的分类全部正确，训练得到的SVM模型取得良好的分类效果，实现了对悬挂系统中液压泵的故障诊断。

5 结论

本文首先在AMESim中建立了液压泵的故障模型和悬挂液压系统模型，分析了液压泵故障对系统流量的影响，并从仿真中获取样本数据，相比于从实际系统中获取数据成本更低、更方便；然后使用小波包分析、主成分分析与支持向量机结合的方法，完成对液压泵的故障诊断并取得较好的结果，为实际应用中SPMT悬挂液压系统液压泵故障诊断提供了方法和依据。本文的故障诊断是基于仿真数据，不能完全真实反映实际系统的情况，在以后的研究中可以对模型和参数设置进行优化使更接近实际系统，使研究结论更加可靠。