Spark下的分布式粗糙集属性约简算法

章夏杰，朱敬华，2*，陈 杨

（1.黑龙江大学计算机科学技术学院，哈尔滨150080；2.黑龙江省数据库与并行计算重点实验室，哈尔滨150080）

0 引言

在高速信息化的时代，由于数据集的体积、多样性和复杂性都在不断增加，特征选择作为从大量无意义的数据中提取有价值信息的一种重要手段已然成为一个研究热点［1-2］。将粗糙集理论［3］应用于特征选择，是一种先进又有效的技术。

找到最小约简的最基本解决方案是生成所有可能的约简并选择具有最大依赖度、最小属性数的约简，这可以通过从数据集构建一种可辨别函数并简化来实现。显然，这种解决方案非常昂贵，仅适用于非常小的数据集。结果表明，最小约简生成是一个NP-hard 问题，因此目前的粗糙集约简算法一般都与爬山式算法或随机算法相结合。

Hu 等［4］提出了一种基于正区域属性重要性的约简算法。Hu 等［5］利用可分辨矩阵中的启发式思想计算属性的重要性，并提出了一种启发式的约简算法。基于正区域和基于条件熵的方法的目的都是选择一个最小特征子集，且该子集能最大化描述给定数据集中的分类信息。基于可辨矩阵的方法是选择一个具有高分辨能力的特征子集，从而保证了约简后的数据集具有最大的类间可分性。这些方法考虑了最佳候选属性，试图找到最小约简。

爬山式的粗糙集约简方法通常以空集或属性核为起点，采用正向选择的方式依次从候选集合中添加最重要的属性直到无法再添加新的属性为止，这种方法速度较快，但是在处理存在较多关联属性的数据集时易陷入局部最优解。

因此一些研究者尝试将随机方法与粗糙集属性约简相结合。Wroblewski［6］尝试结合遗传算法来搜索最小约简并得到了精度较高的约简结果；Jensen等［7］使用另一种随机策略——蚁群优化算法来寻找最小属性约简，在速度与精度上有一定的提升；Wang 等［8］使用了一种元启发算法——粒子群算法来寻找最小属性约简，在精度上得到了进一步提高。然而该类方法需要大量的迭代计算，因此在处理大数据集时非常耗时。

为了在合理时间内得到较高精度的结果，有必要使用分布式技术。Spark是一种崭新的大数据并行计算框架，它基于内存计算，提高了在大数据环境下数据处理的实时性，同时保证了高容错性和高可伸缩性，允许用户将Spark部署在大量廉价硬件之上，形成集群。与Hadoop 的MapReduce 相比，Spark基于内存的运算要快100倍以上。

Dagdia 等［9］在2017 年提出了一种基于Spark 平台的分布式粗糙集算法SP-RST。该算法通过将属性分区后求得局部约简，再将局部约简结果合并的方式有效减少了属性约简所需的时间。该算法中的分区数会直接影响算法的精度与执行速度。我们在实验中发现：增大分区数量虽然能提高执行速度，但是能够约简掉的冗余属性将会越少，导致精度下降；而且该算法在可接受的运行时间内，约简质量较低。

综上，为了能够在合理的时间内处理大数据集并得到较高精度的结果，在Spark平台上实现了一种元启发式的分布式粗糙集属性约简算法SP-WOFRST，该算法结合了笔者新提出的一种依赖计算方法——快速依赖计算（Fast Dependence Computing，FDC）来计算属性子集的依赖度，并通过改进的鲸鱼优化算法（Whale Optimization Algorithm，WOA）来寻找最优属性子集。最后在两组人工合成的大数据集上对本文算法的性能进行了验证，结果表明本文算法相比SP-RST 算法在精度和速度上都有明显的性能提升。

1 粗糙集与依赖度计算

1.1 粗糙集

定义1不可分辨关系［10］。给定决策表S=(U，A，V，f)，对于每个属性子集R ⊆A，定义了一个不可分辨关系IND(R)，即显然，不可分辨关系是一种等价关系。

定义2上下近似集［10］。给定决策表S=(U，A，V，f)，对于每个子集X ⊆U 和一个不可分辨关系R ∈ind(K)，定义X 的R上下近似集分别为：

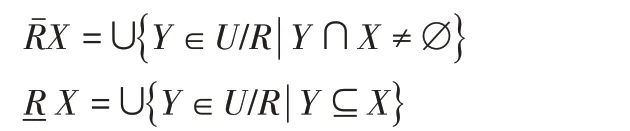
定义3相对正区域［10］。设P 与Q 为U 上的两个等价关系，Q的P正域POSp(Q)，定义为

定义4k 度依赖。设P 与Q 为U 上的两个等价关系，若依赖度，则称Q 是k(0 ≤k ≤1)度依赖于P的。

1.2 依赖度计算

传统计算依赖度的方法分为三步：第一步计算以决策属性构建的等价类U/D，第二步计算以条件属性构建的等价类U/C，第三步通过计算相对正域求出依赖度。下面以表1为例加以说明。

设表1 中的肤色与瞳色为条件属性，出生地（birthplace）为决策属性。

第一步 通过决策属性进行分类可以得到等价类U/D={D1，D2，D3，D4}，其 中：D1={X1，X2}；D2={X3，X5}；D3={X4，X6}；D4={X7，X8}。

表1 决策表Tab.1 Decision table

第二步 通过条件属性｛肤色，瞳色｝进行分类可得到等价类U/C={C1，C2，C3}，其中：C1={X1，X2}；C2={X3，X5}；C3={X4，X6，X7，X8}。

第三步 需要求出相对正域，即从P 中筛选出Q 的子集：C1 ⊆D1；C2 ⊆D2。

因此，最终求得的依赖度为：

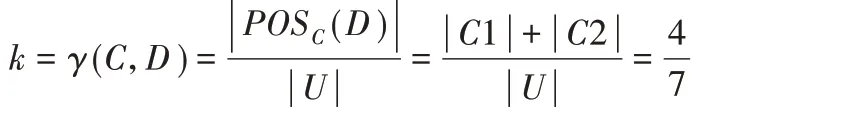
1.3 快速依赖计算

与传统的通过正域求依赖的方法不同，快速依赖计算（FDC）通过直接比较不同类别对象的属性来分辨对象是否属于唯一类，最后统计该类对象即可求出依赖度。仍以表1 中的数据为例进行讲解。

步骤1 对决策表进行预处理，将决策类属性转换成整型，并赋予每个对象唯一编号，额外添加一个标记，默认值为0。预处理结果如表2所示。

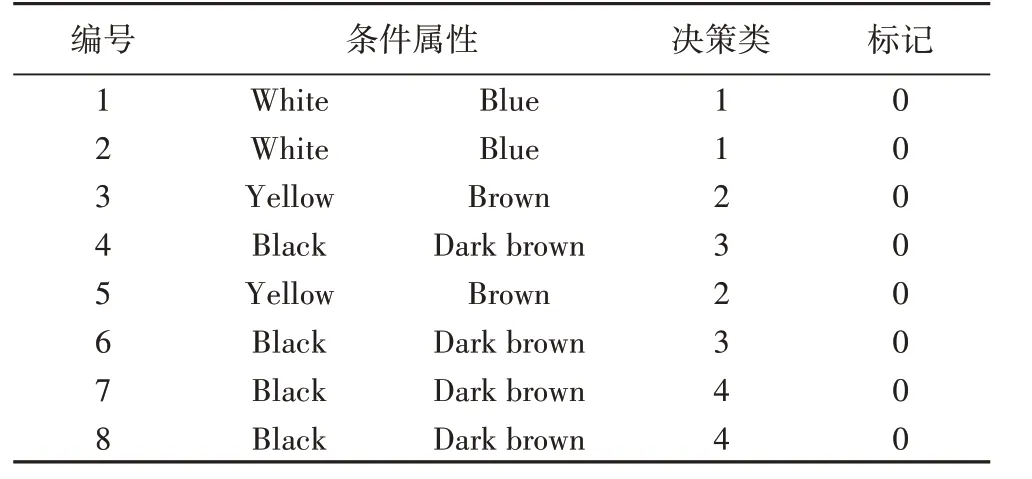
表2 表1的预处理结果Tab.2 Results after preprocessing for Tab.1

步骤2 让每个对象Xi（即编号为i的对象）与表中其余对象Xj作比较，若Xi的决策属性大于Xj，则比较Xi与Xj的条件属性。若条件属性完全相同，将Xi与Xj的标记改为1；若存在不同属性值，则直接进入下一轮比较。执行结果如表3所示。

步骤3 遍历决策表，统计标记为0的对象即可求出属于正的对象数，进而求得依赖度：

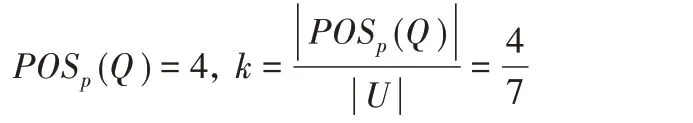
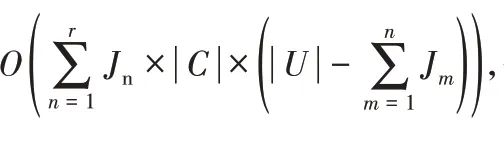
表3 执行步骤2后的结果Tab.3 Results after step 2

算法1 描述了在Spark 平台下FDC 算法的实现。由于Spark 中的广播变量是不可修改的，因此需额外创建一个sign数组保存标记信息，其长度等于样本总数。

循环遍历广播变量TD，对满足条件obj1.lable ＞obj2.lable的对象比较条件属性，若条件属性完全相同，则以对象id为索引，将sign 数组指定下标位置上的数值变更为1。最后统计sign数组中值为0的总个数即可求出依赖度。

算法1 快速依赖计算（FDC）。

输入 搜索代理SearchAgent；

输出 依赖度Dependency。

2 鲸鱼优化算法及其改进

2.1 鲸鱼优化算法

鲸鱼优化算法（WOA）［11］通过模拟座头鲸捕食行为实现对目标问题的求解。经相关实验证明，WOA 在收敛速度以及全局搜索能力上都要优于粒子群优化算法［12］和遗传算法等经典算法，并且在特征选择领域也得到了更高的精度［13］，因此本文将该算法应用到粗糙集属性约简中，以提高约简效率。

WOA 主要可分为包围猎物、泡泡网攻击以及搜索猎物三个不同阶段。

2.1.1 包围猎物

WOA 假设种群中当前适应度最高的个体所在位置为当前猎物的位置，即本轮迭代中的最优解；在确定猎物之后，种群中的其他鲸鱼将根据当前猎物的位置来更新自身位置，数学模型如下：

其中：t 表示当前迭代数；X*代表当前群体中最优解的位置向量；X(t)表示鲸鱼当前所在的位置向量，Α ⋅D 表示包围的步长，A和C为系数向量，其定义如式（3）、（4）。

其中：r1与r2为［0，1］范围内的随机数；a的取值随迭代次数增加而减小，由2递减为0，表示如式（5）。

其中Max_iter代表最大迭代次数。

2.1.2 泡泡网攻击

依据座头鲸的捕猎特点，WOA 设计了收缩包围以及螺旋更新位置两种策略来模拟泡泡网攻击行为。

1）收缩包围机制通过减小式（3）中a 的取值来实现。由式（3）可知，A的取值在[-a，a]区间，A随着a减小而减小。

2）螺旋更新位置首先需计算鲸鱼与猎物之间的距离，然后在鲸鱼与猎物之间创建螺旋方程以模仿座头鲸的螺旋运动，数学模型如下：

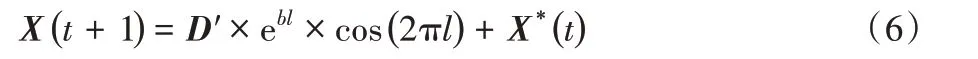
为了模拟鲸鱼在收缩包围的同时，还沿着螺旋路径移动，算法假设鲸鱼在进行狩猎的过程中选择两种策略的概率都为0.5，其数学模型可表示为：

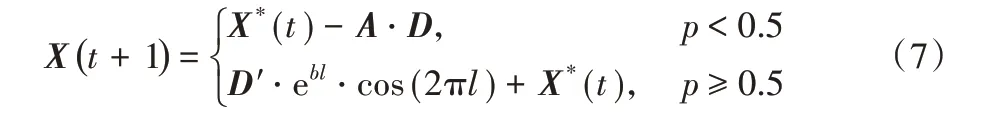
2.1.3 搜索猎物

当A 满足 |A |＞1 时，鲸鱼通过彼此的位置随机搜索猎物。通过这种方式可以增强WOA 的全局寻优能力。其数学模型表示如下：

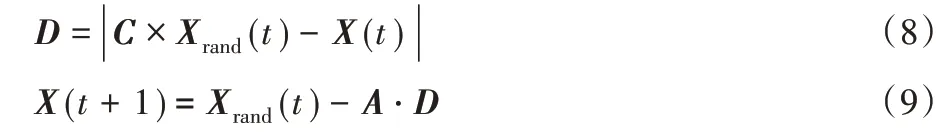
2.2 应用与改进

为了将WOA有效地应用到粗糙集属性约简当中，必须对其进行一定的改进。

在属性约简（或称特征选择）中对于每个特征只有“选”与“不选”两种情况。使用一个长度为特征总数的一维数组来表示种群中的个体，每个个体即为问题的一个解。数组中的每个单元格都有一个值“1”或“0”。值“1”表示选择了相应的特征，值“0”表示未选择相应的特征。

以两个特征子集向量相减后的非0 元素个数作为特征子集之间的距离。比如［0，1，0，1］与［1，0，1，1］之间的距离为3。

在元启发算法中，需要通过适应度来判断种群个体的优劣。在本文算法中适应度函数表示如下：

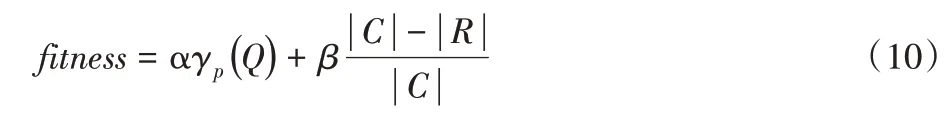
其中：α和β 的值在［0，1］范围内，且α+β=1；|R |为选中的特征个数；|C |为总特征数；γp(Q)为依赖度。本文取α=0.99，β=0.01。

在初期实验中发现将WOA 应用于粗糙集属性约简时会出现过早收敛的现象，因此在收缩包围与螺旋更新操作后加入了变异算子来提高算法的全局搜索能力。其中变异率为：

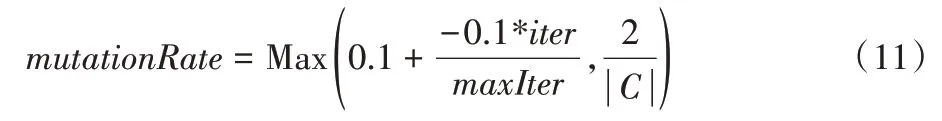
其中：iter 代表当前迭代次数，maxIter 代表最大迭代次数，| |C代表特征总数。

改进后的鲸鱼优化算法如算法2所示。其中：第2）～9）行为初始化相关参数；第6）、7）行为搜索猎物阶段，对应式（8）、（9）；第9）、10）行描述包围阶段，对应式（1）、（2）；第15）～17）行描述螺旋更新，对应式（6）。另外，在收缩包围与螺旋更新完毕后加入了变异算子，如算法3 所示，通过式（11）计算出本轮迭代的变异率，对种群个体的部分值做0-1变换。

算法2 改进后的WOA（WOAcore）。

输入 搜索代理数组 searchAgents，最佳搜索代理bestSearchAgent，最大迭代次数maxIter和当前迭代次数iter；

算法3 Mutation。

输入 搜索代理searchAgent，最大迭代次数maxIter 和当前迭代次数iter；

3 SP-WOFRST算法

将FDC 与改进的WOA 结合来寻找最优属性子集，并在Spark 平台上并行实现，得到SP-WOFRST 算法的主要流程如图1所示。其中：输入参数table是预处理后的决策表，输出结果为约简后的最佳属性子集。

首先，将table 以广播变量的形式送到每一个计算节点，即每个计算节点上仅保留一份预处理后的决策表。然后初始化种群并转化为RDD 对象，通过Spark 的map 算子将种群中的个体分发到各个计算节点，使用FDC 算法在每一个计算节点上并行求解每一个个体的依赖度。一轮迭代结束后，收集各个节点的个体依赖度计算结果，选出本轮最佳个体，通过WOA 的搜寻机制更新其余个体后再次进入新一轮的迭代。经过指定迭代次数后算法结束，获得全局最佳个体，即最终的约简结果。

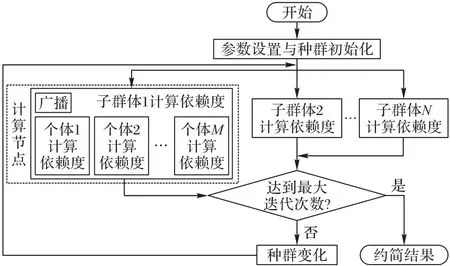
图1 SP-WOFRST流程Fig.1 Flowchart of SP-WOFRST

算法4 SP-WOFRST。

输入 预处理后的决策表table，种群个体数量searchAgentsNum，WOA最大迭代次数maxIter；

输出 最终约简结果Reduct。

4 实验结果与分析

在分布式环境下对算法SP-WOFRST 与SP-RST 在多种参数设置下分别进行实验，并对两种算法在各自最优参数设置下的实验结果作对比分析。此外还对比了SP-WOFRST 算法在不同节点数下的运行时间。

4.1 数据集

算法SP-WOFRST 与SP-RST 都基于经典粗糙集理论（Pawlak 粗糙集模型［3］），它们所处理的分类必须是完全正确的或肯定的，因为它是严格按照等价类来分类的，因而它的分类是精确的，亦即“包含”或“不包含”，而没有某种程度上的“包含”或“属于”，因此对噪声的处理能力较弱。UCI 上的高维数据集大部分无法满足上述要求，并不适合用于本文的算法测试，而低维数据集虽然符合要求，但由于数据量过少，难以展现实验结果。因此使用了两个人工数据集arsds1 与arsds2 来测试算法的性能，数据集相关属性见表4。arsds1 是一个高冗余度的数据集，其中包含50 个互不冗余的必要特征，400 个冗余特征以及50 个无关特征；arsds2 中包含250 个互不冗余的必要特征，200 个冗余特征以及50 个无关特征。即在理想情况下，对两个数据集作特征选择的结果中应当分别包含50个或250个必要特征。

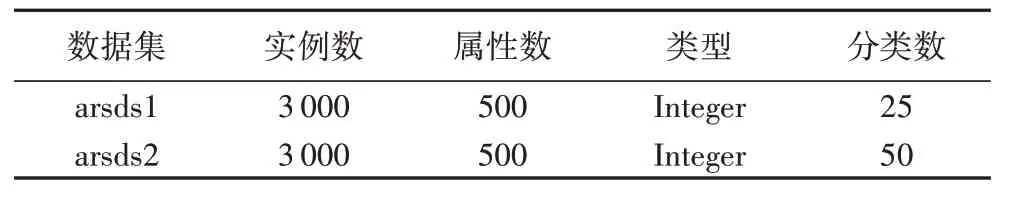
表4 实验数据集Table 4 Experimental datasets

在检验特征选择算法的有效性时，使用人工数据集有以下两个优势［14］：

1）预先已知最优的特征组合，因此可以精确地评估算法结果的精确性。

2）实验数据是可控的，可以通过系统地改变所选择的实验条件来进行不同的实验，比如在数据集中添加或减少更多不相关的特征或噪声，这将有助于得出更有用的结论，并测试现有算法的优缺点。

4.2 实验配置

硬件方面使用3 台搭载I5-4590，主频3.30 GHz 的CPU，8 GB 内存的计算机，算法均在Spark 2.1.1 平台上用Scala 2.11实现。

4.3 度量标准

由于使用人工数据集进行实验，预先已知特征之间的相关性以及各个特征的有用性，因此无需使用其他分类算法来测量约简结果的精确度。本文采用F1-Measure作为约简结果的质量指标，计算公式定义如下：

其中：TP（真正例）指约简结果中选中的必要特征，FP（假正例）指约简结果中未选中的必要特征，FN（假反例）指约简结果中未能剔除的冗余/无关特征，TN（真反例）指约简结果中正确剔除的冗余/无关特征；P 为查准率（Precision），指约简结果中选中的必要特征占有用特征总数的比例；R 为查全率（Recall），指约简结果中选中的必要特征占约简结果总特征数的比例。

4.4 结果分析

第一项实验中使用3 台机器分别对SP-RST 与SPWOFRST 在不同的参数设置（算法自身有两个需要人为调节的参数）下进行实验，表5～8 中列出了最优的几项实验结果，其中加粗项为全局最优的实验结果。第二项实验在不同的节点数下对SP-WOFRST算法的运行效率进行了统计分析。

在Spark 平台下，算法的最大实际并行度等于CPU 的总核心数，即第一项实验中共有12 个核心在并行执行算法，并且SP-WOFRST算法中需要网络传输的数据量非常少，因此在增加节点时，执行效率接近线性提升。

表5 与表6 分别为不同参数设置下的SP-RST 算法在arsds1 与arsds2 数据集上的实验结果。“特征数/分区”指该算法定义的每个分区内的特征数，该参数越大则算法精度越高，速度越慢。由于该算法最后需要对多次迭代得到的多个约简结果求交集，该算法在执行过程中必然会漏选个别必要特征。

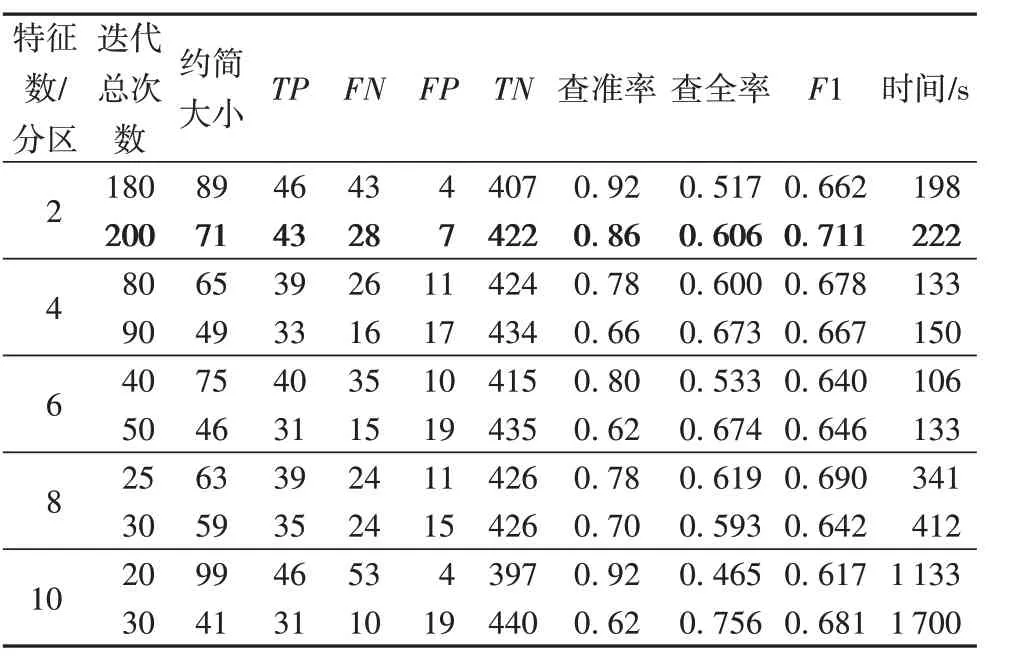
表5 不同参数设置下的SP-RST在arsds1数据集上的性能Tab.5 Performance of SP-RST on arsds1 dataset with different parameter settings

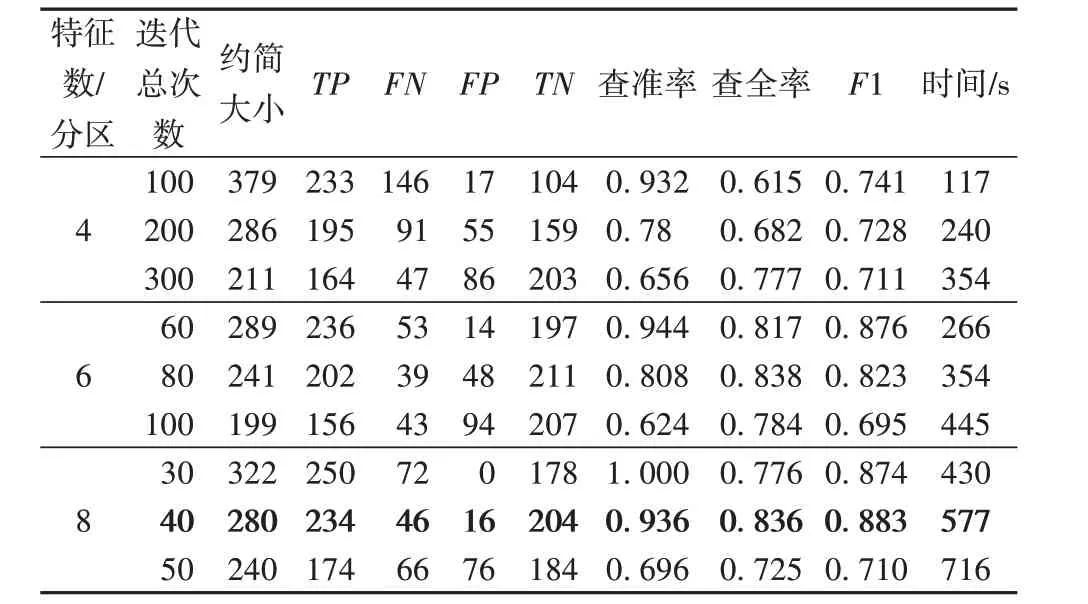
表6 不同参数设置下的SP-RST在arsds2数据集上的性能Tab.6 Performance of SP-RST on arsds2 dataset with different parameter settings

表7与表8分别为不同参数设置下的SP-WOFRST算法在arsds1 与arsds2 数据集上的实验结果。由于在适应度函数中取α=0.99，β=0.01，因此算法会优先选择依赖度高的约简结果，所以在表中可以看到查准率始终为1。通过对比F1 与时间两项结果，可以清晰地看出，在相近的运行时间下，SP-WOFRST的精度均优于SP-RST。

第二项实验的结果如图2 所示，在不同节点数下，SPWOFRST 算法执行50 次迭代所需的时间随着节点数的增加呈线性递减，说明本文提出的算法在小型集群上可扩展性良好。

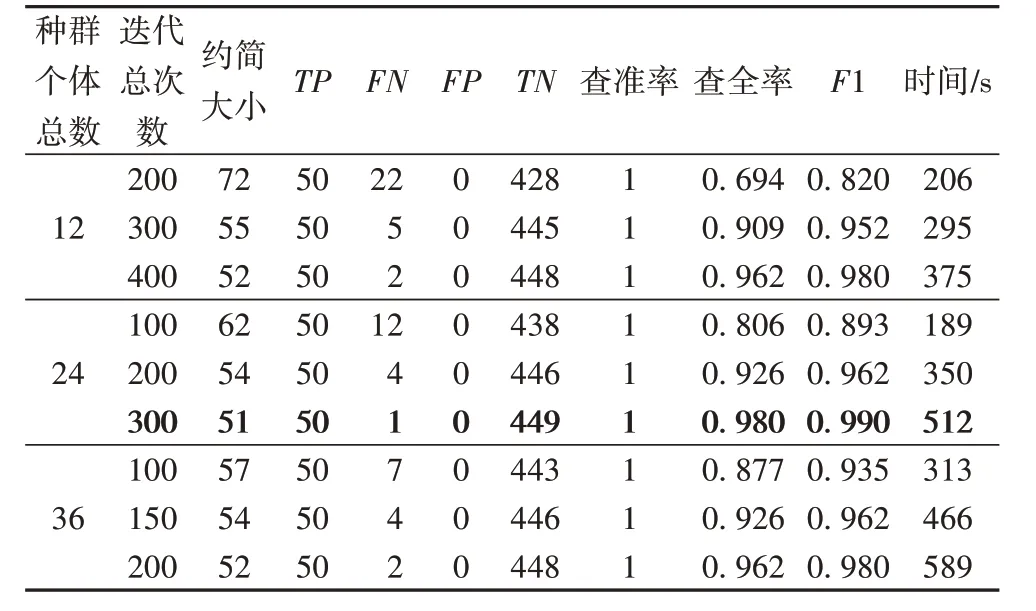
表7 不同参数设置下的SP-WOFRST在arsds1数据集上的性能Tab.7 Performance of SP-WOFRST on arsds1 dataset with different parameter settings

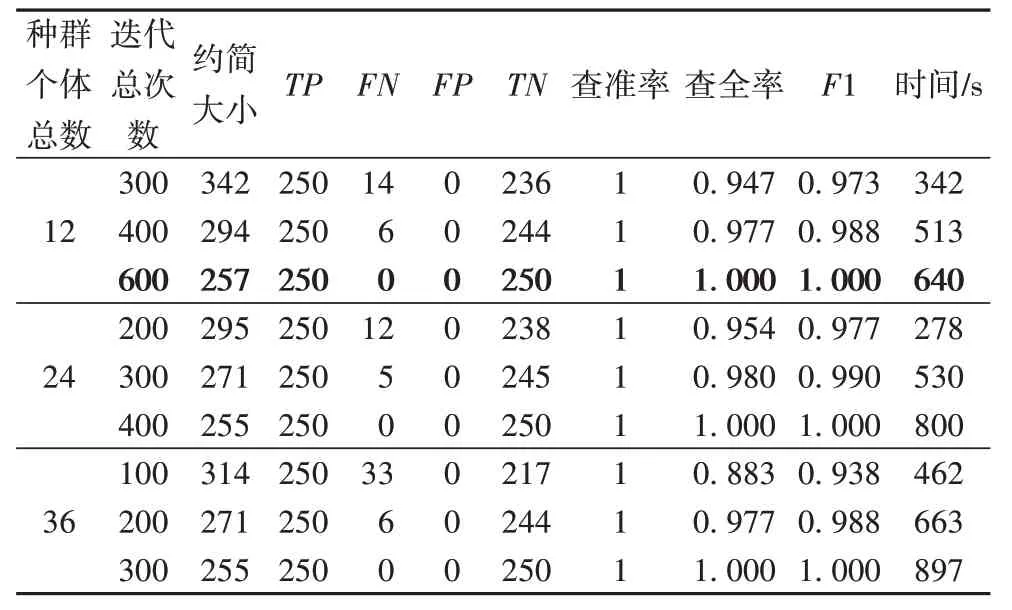
表8 不同参数设置下的SP-WOFRST在arsds2数据集上的性能Tab.8 Performance of SP-WOFRST on arsds2 dataset with different parameter settings

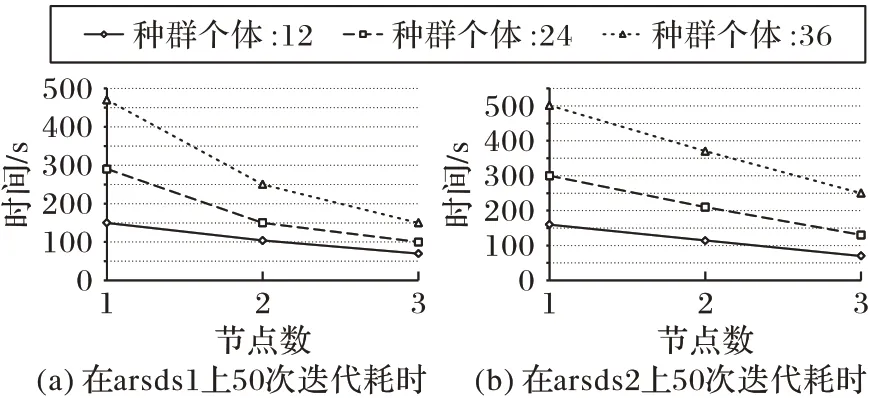
图2 SP-WOFRST算法在不同节点数下的运行时间Fig.2 Running time of SP-WOFRS algorithm under different node numbers

5 结语

本文提出了一种基于Spark 平台的高效分布式粗糙集属性约简算法SP-WOFRST。该算法通过鲸鱼优化算法（WOA）寻找最优特征子集，并使用更快速的依赖计算方法FDC 来提高计算速度，在保持较高精度的前提下大大缩短了算法执行时间。实验结果表明，相较于现有的分布式粗糙集特征选择算法，在相近的运行时间下本文算法有更高的精度。在后续研究中，我们将尝试利用变精度粗糙集理论改进本文算法，使算法能够更好地适应带噪声的数据集，进一步提高算法的精确度。我们计划在未来实现变精度［15］以及基于信息熵［16］的分布式粗糙集约简算法。