低冗余计算的可达性查询保持图压缩策略
2020-04-09赵丹枫林俊辰黄冬梅
赵丹枫,林俊辰,宋 巍,王 建,黄冬梅
(1.上海海洋大学信息学院,上海201306;2.上海电力大学,上海200090)
0 引言
近年来,随着计算机技术和网络技术的发展,现实生活中很多领域产生了越来越多的网络数据,如语义网[1]、万维网[2]、道路网[3]、推荐网[4]、社交网[5]以及生物信息网[6]等,并且这些网络中的数据结构趋于复杂,难以用关系数据模型描述。图作为一种能够有效描述事物之间复杂关系的数据结构,在上述领域得到了广泛的研究和应用。
可达性查询是图问题研究中一种基本的查询方法,很多复杂的图查询问题通常建立在可达性查询的基础上,可达性查询一直是数据库领域研究的热点,与其相关的研究已经进行了二十多年[7-11]。随着大数据时代[12-13]的到来,图数据的规模不断扩大,对可达性查询的求解提出了新的挑战。以微信数据[14]为例,据腾讯官方统计,截至2018 年9 月,全球微信用户已超过10 亿8 千万,用户平均好友数超过130 个。若采用邻接表来存储由微信用户形成的社交网络,需要超过1 TB 的存储空间,在研究中难以满足这样的内存需求,因而不能将邻接表全部载入内存后对可达性查询求解。
针对图数据规模增大引发的查询难问题,主要有以下三种解决方法[15]:1)使用硬盘存储图数据,每次载入部分图数据到内存中,分步查询,最后整合结果;2)使用分布式系统存储图数据,每个节点进行部分查询,最后整合结果;3)将图数据进行压缩表示,全部载入内存中,直接查询得到结果。
以上三种解决方法各有优劣。第一种方法适用于访问局部性较好的图数据,若图数据访问局部性较差,则在查询时I/O 次数会显著增多,从而导致查询代价增大;第二种方法适用于耦合性较低的图数据,若图数据耦合性较高,则会造成数据难以分割,且分割后各子图相关性较大及通信次数显著增多等问题,从而导致查询代价增大;第三种方法并不能解决所有的问题,对于某些规模特别大的图数据来说,压缩后依然不能全部载入内存中进行计算,但是,它可以和前两种方法有机结合,进一步改善前两种方法的性能。针对第一种方法,若在保持访问局部性的前提下先对图数据进行压缩,可以减少I/O次数,从而提高访问速度;针对第二种方法,若先对图数据进行压缩,则分布式系统可以利用更少的节点完成相同的任务,并且可以减少节点间的通信次数。因此,可达性查询保持图压缩是解决大规模图数据上可达性查询难问题的有效途径。
但现有的可达性查询保持图压缩方法存在冗余计算,因而计算效率较低,随着数据量的增大,时间消耗变得难以接受,所以有必要研究新的压缩策略,提高压缩速度。
本文的主要工作如下:
1)针对求解祖先后代集过程设计了一种基于拓扑排序的祖先后代集求解算法(Topological Sorting Based algorithm for solving ancestor and descendant sets,TSB),能有效地减少冗余计算,加快求解速度;还设计了一种基于图聚合运算的祖先后代集求解算法(AGGregation Based algorithm for solving ancestor and descendant sets,AGGB),对最长路径长度较小的图数据有较好效果。
2)针对求解可达性等价类过程设计了一种分段统计剪枝(Piecewise Statistical Pruning,PSP)算法,实现了可达性等价类求解过程的剪枝,减少了冗余匹配,加快了求解速度。
3)应用不同数据集进行实验,结果表明,本文提出的可达性查询保持图压缩策略是高效、快速的。
1 相关工作
对图数据进行高效、紧凑的表示与压缩是当前图研究的热点之一,同时也为图上的其他基本算法和操作提供了强有力的支持,包括存储空间优化、查询优化及可视化分析等。
1.1 图压缩技术的分类
文献[15]中将图压缩技术分为四类:基于传统存储结构的压缩技术、网页图压缩技术、社交网络图压缩技术和面向特定查询的图压缩技术。文献[16]中对此作了进一步归纳,将图压缩技术分为三类:基于图数据外在特点的压缩技术、基于图数据内在特点的压缩技术和面向特定查询需求的压缩技术。
1)基于图数据外在特点的压缩技术。图数据的外在特点是指图的表示形式或图的存储结构。传统的图数据表现形式和存储结构主要包括邻接矩阵、邻接链表、邻接多重表、十字链表等。文献[17-19]中针对图数据邻接矩阵的稀疏性对其进行压缩,文献[20]中则通过压缩处理图数据的邻接链表中存储的冗余信息来实现图压缩;但是上述这几种压缩方法均改变了图数据的存储结构,通常不利于查询。
2)基于图数据内在特点的压缩技术。图数据的内在特点是指由于应用领域的不同,图数据所具有的不同的内在性质。例如,对社交网络图而言,可以利用社交网络中的社区结构特性对图数据进行压缩[21],具体表现为社区内相关性强,而社区间相关性弱;再如,对网页图而言,可以利用其本地性和相似性压缩图数据[22-24];此外,在可视化分析领域,文献[25-27]中针对数据图稠密的特性,开发了相应的稠密有向图压缩算法。
3)面向特定查询需求的压缩技术。查询是图数据研究中的基本操作,一直是图领域中的研究热点。常用的图上查询有可达性查询、内外邻居查询和图模式匹配等。为了达到更低的压缩比[28],将不可避免地引起一些信息损失。因此,对面向特定查询的压缩图来说,压缩图与原图是一种基于特定查询的等价图[29]。
1.2 可达性查询保持的图压缩技术
可达性查询保持的图压缩是Fan 等[30]提出的概念,是一种面向可达性查询的压缩技术,这种压缩技术追求极低的压缩比,与此同时,保证了压缩图对可达性查询保持结果不变,即其压缩图与原图针对可达性查询是等价的。文献[30]提出的可达性查询保持图压缩(Query Preserving Graph Compression,QPGC)算法,使用广度优先遍历(Breadth-First Search,BFS)[31]的方法计算原图中每个顶点的祖先顶点集和后代顶点集,由于具有相同祖先和后代的顶点关于可达性查询是等价的,因此遍历各顶点可确定可达性等价关系。文献[30]同时提出了一种优化策略:先计算原图中的强连通分量,将其压缩为一个虚拟顶点,得到一个有向无环图(Directed Acyclic Graph,DAG)[32],将此DAG 作为算法的输入,最终获得可达性查询保持图。该算法随着图数据规模的增大,表现逐渐不佳,耗时显著增大。因为QPGC 算法通过BFS 方法计算各顶点的祖先顶点集和后代顶点集的过程中存在冗余计算,而且BFS结果集比较庞大,导致可达性等价类的计算存在一定局限性。文献[16]在QPGC 算法的基础上,结合MapReduce[33]的思想,提出了适合于MapReduce 的可达性查询保持图计算方法,但是并没有提高计算速度。文献[34]中提出了一种基于BFS 结果集的可达性保持图并行计算方法,但是该方法的主体为基于BFS 结果集的SCC 查找算法,仅考虑压缩原图中存在的强连通分量(Strongly Connected Components,SCC),不能达到QPGC算法的压缩比。
在本文提出的低冗余计算低的可达性查询保持图压缩策略的压缩过程中,着重考虑避免进行冗余计算,提高计算效率,以实现求解过程的加速,显著提高压缩速度。
2 本文方法
在求解祖先后代集过程和求解可达性等价类过程中,本文分别设计了高效、低冗余的求解算法。
2.1 高效的祖先后代集求解方法
在提出本文方法之前,首先对现有QPGC 算法求解祖先集和后代集过程中存在的问题进行分析。
QPGC 算法以每个顶点为初始顶点,使用向前或向后的BFS 方法,分别求出其祖先顶点集和后代顶点集,要进行2|V|次BFS遍历。事实上,每个顶点的祖先(后代)集与其前驱(后继)顶点的祖先(后代)集具有一定的联系,算法在不同的遍历顺序下执行时间大不相同,下面举例说明。
例1 考虑图1 所示的示例,使用BFS 方法求解各顶点的后代集,若遍历顺序为E、A、B、C、D,则:在计算顶点E 的后代时,进行了4 次访问,后代集为{B,C,D};计算顶点A 的后代时,进行了4 次访问,后代集为{B,C,D};计算顶点B 的后代时,进行了3 次访问,后代集为{C,D};计算顶点C 的后代时,进行了2次访问,后代集为{D};计算顶点D的后代时,进行了1 次访问。共进行了14 次访问。然而,若按D、C、B、E、A 的顺序求解,则只需进行9 次访问。这种冗余随着图的规模增大,将会进一步增大。
针对现有方法由冗余计算引起的求解祖先后代集速度慢的问题,本文提出了两种算法TSB 和AGGB,分别适用于一般的图数据和最长路径长度较小的图数据,下面分别说明。
2.1.1 基于拓扑排序的祖先后代集求解算法TSB
在描述算法前,首先介绍拓扑排序的定义及拓扑序列具有的性质。
定义1拓扑排序是定义在DAG 上的一种排序,其将图G=(V,E)中所有顶点排成一个线性序列,使得对图中任意一对顶点u和v,若(u,v)∈E,则u在该线性序列中出现在v之前。
引理1沿拓扑序列顺序(逆序)求解各顶点的祖先集(后代集),每个顶点与边需要且仅需要访问1次。
证明
以沿拓扑序列顺序求解祖先集为例:
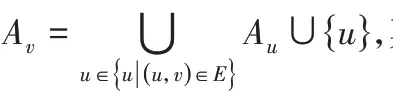
因此,求解v的祖先集,仅需访问v的每个父顶点各1次。
综上所述,沿拓扑序列顺序求解各顶点的祖先集,每个顶点与边需要且仅需要访问1 次。类似地,可以证明沿拓扑序列逆序求解各顶点的后代集,每个顶点与边需要且仅需要访问1次。
本文提出的基于拓扑排序的祖先后代集求解算法TSB如算法1所示。
首先,将原图转化为DAG。在实际应用中,若图数据不是DAG,则不能进行拓扑排序,因此要对其中的环(也即SCC)进行特殊处理,将图数据转化为DAG。Gabow 算法[35]是求解SCC的经典算法,本文使用Gabow算法求解图中的SCC。
然后将每个SCC 用一个单顶点代替,此时图数据变为DAG。
接下来应用BFS 方法对DAG 进行拓扑排序,得到拓扑序列。过程简述如下:取一未访问过的入度为0 的顶点,该顶点必为DAG 中某一棵树(连通分量)的根顶点,应用BFS 方法遍历此树;重复这一步骤,直到不存在未访问过的顶点。顶点的遍历顺序即为拓扑序列。
最后,沿拓扑序列顺序求解各顶点的祖先集,沿拓扑序列逆序求解各顶点的后代集。
TSB和QPGC算法均使用了BFS方法对图数据进行遍历,区别在于:QPGC 算法由每个顶点为初始点,应用BFS 方法遍历至最底层或最顶层,从而求得其祖先或后代顶点集;而TSB取根节点为初始点,使用一次BFS 遍历求得DAG 的拓扑序列,沿拓扑序列顺序或逆序求解各顶点的祖先后代顶点集,当求解某顶点时,仅需访问该顶点的邻接顶点即可完成求解。
算法1 TSB。
输入 图G=(V,E);
输出 祖先顶点集AG和后代顶点集DG。
1)使用Gabow算法求解SCC;
2)压缩每个SCC 为一个单顶点,得到与原图对应的DAG;
3)应用BFS方法对DAG拓扑排序,得到拓扑序列;
4)沿拓扑序列顺序(逆序)求解祖先集(后代集)。
例2 考虑图2(a)所示的例图,首先使用Gabow 算法求得SCC 为{5},{6},{1,2,3},{4};压缩SCC 得到DAG 如图2(b);应用BFS 方法对DAG 拓扑排序,得到拓扑序列5,6,a,4(不唯一);沿拓扑序顺序求解祖先顶点集,计算5 的祖先集为∅,访问1 次,计算6 的祖先集为∅,访问1 次,计算a 的祖先集为{5,6,a},访问3 次,计算4 的祖先集为{5,6,a},访问2 次,共访问7 次;沿拓扑序逆序求解后代顶点集,计算4 的后代集为∅,访问1 次,计算a 的后代集为{a,4},访问2 次,计算6 的后代集为{a,4},访问2 次,计算5 的后代集为{a,4},访问2次,共访问7次。

图2 TSB例图Fig.2 Example of TSB algorithm
2.1.2 基于图聚合运算的祖先后代集求解算法
基于图聚合运算的祖先后代集求解算法AGGB 如算法2所示。
首先初始化各个顶点的祖先集和后代集为空集;接下来每个顶点分别向其父(子)顶点发送其后代(祖先)集;每个顶点接收到消息后,更新其自身的后代(祖先)集为原后代(祖先)集和其接收到的后代(祖先)集以及其子(父)顶点集的并集;重复发送—接收—更新的过程,直至所有顶点的后代集和祖先集均不再发生变化,算法结束。
AGGB 的聚合运算次数与图数据最长路径长度具有正相关关系,因此适用于最长路径长度较小的图数据。
算法2 AGGB。
输入 图G=(V,E);
输出 祖先顶点集AG和后代顶点集DG。
1)初始化每个顶点的祖先集和后代集为空集;
2)每个顶点向其父顶点和子顶点分别发送其后代集和祖先集;
3)每个顶点接收其父顶点和子顶点发送的后代集和祖先集,更新自身的祖先集和后代集;
4)重复步骤2)、3),直到每个顶点的祖先集和后代集均不再发生变化。
例3 仍考虑图2(a)所示的例图。应用AGGB:第1 次聚合运算得到各顶点的祖先集(括号内,下同)为5(∅),6(∅),2({3,5,6}),1({2}),3({1}),4({1,3}),后代集(括号内,下同)为5({2}),6({2}),2({1}),1({3,4}),3({2,4}),4(∅);第2 次聚合运算得到的祖先集为5(∅),6(∅),2({1,3,5,6}),1({2,3,5,6}),3({1,2}),4({1,2,3}),后代集为5({1,2}),6({1,2}),2({1,3,4}),1({2,3,4}),3({1,2,4}),4(∅);第3次聚合运算得到的祖先集为5(∅),6(∅),2({1,2,3,5,6}),1({1,2,3,5,6}),3({1,2,3,5,6}),4({1,2,3,5,6}),后代集为5({1,2,3,4}),6({1,2,3,4}),2({1,2,3,4}),1({1,2,3,4}),3({1,2,3,4}),4(∅);第4 次聚合运算得到的祖先集为5(∅),6(∅),2({1,2,3,5,6}),1({1,2,3,5,6}),3(1,2,3,5,6),4({1,2,3,5,6}),后代集为5({1,2,3,4}),6({1,2,3,4}),2({1,2,3,4}),1({1,2,3,4}),3({1,2,3,4}),4(∅)。祖先顶点集和后代顶点集均不再发生变化,求解结束,共进行了4次聚合运算。
2.1.3 算法性能对比分析
1)时间复杂度。
QPGC:对使用邻接表存储的图数据,使用BFS 方法将顶点遍历一次的时间复杂度为O(|V|+|E|),而QPGC 算法求解祖先后代集时需对每个顶点分别进行一次向前(向后)的BFS遍历,从而获得当前顶点的祖先(后代)集,因此时间复杂度为O(|V|⋅(|V|+|E|))。
TSB:使用Gabow 算法求解SCC 时,对每个顶点和边访问1 次,时间复杂度为O(|V|+|E|)。压缩SCC 为单顶点的时间复杂度为O(n),其中n 为SCC 的个数(n ≤|V|)。使用BFS 方法对顶点拓扑排序时,对每个顶点和边访问1 次,时间复杂度为O(|V|+|E|)。沿拓扑序列顺序求解祖先集时,对每个顶点和边访问1 次,求解后代集亦然,时间复杂度为O(|V|+|E|)。因此TSB的时间复杂度为O(|V|+|E|)。
AGGB:算法需要最多不超过图数据最长路径长度次数的聚合运算,每次聚合运算访问顶点和边各两次,时间复杂度为O(|V|+|E|),因此,AGGB的时间复杂度为O(|V|+|E|)。
2)空间复杂度。
QPGC:算法使用BFS 方法遍历图数据,需要使用一个队列,空间复杂度为O(|V|)。
TSB:算法使用Gabow算法求解SCC时,需使用两个栈,此步骤空间复杂度为O(|V|);算法求得的DAG 需使用邻接表存储,此步骤空间复杂度为O(|V|+|E|);算法使用BFS 方法求拓扑序列,需使用一个队列,此步骤空间复杂度为O(|V|);算法存储拓扑序列需使用一个数组,此步骤空间复杂度为O(|V|)。因此,TSB空间复杂度为O(|V|+|E|)。
AGGB:算法可直接在祖先后代结果集上进行操作,因此空间复杂度为O(1)。
分析三种算法的时间复杂度和空间复杂度,可以得出以下结论:与QPGC 算法相比,TSB 和AGGB 均将时间复杂度由O(|V|⋅(|V|+|E|))降至O(|V|+|E|),其中TSB 以牺牲部分空间为代价,将空间复杂度由O(|V|)提高到O(|V|+|E|),而AGGB 能够进一步将空间复杂度降至O(1)。AGGB 的特性决定其仅适用于最长路径较短的图数据,而TSB的普适性更强。
2.2 分段统计剪枝的可达性等价类求解算法
针对现有算法由BFS结果集(即顶点祖先后代结果集)计算可达性等价类效率低的问题,本文提出了一种分段统计剪枝(PSP)算法(见算法3),可以有效提高可达性等价类的求解速度。首先,确定分段大小S,每S个顶点划分为一个分段;接着对每一个顶点,分别统计其祖先集和后代集落在对应分段内的顶点个数。这个过程可以在计算祖先和后代集的同时进行,每求得当前顶点的一个祖先顶点,就为这一祖先顶点所在的分段的统计值加1,这一过程每次要计算一次除法(计算所在分段)和一次加法。接下来,对每一个顶点对,首先判断二者的统计值是否相同,若不相同,则二者祖先集和后代集必然不同,因此不属于同一可达性等价类,无需进行精细比较,从而达到快速剪枝的效果;若相同,则二者存在祖先集和后代集相同的可能,进一步精细比较二者的祖先集和后代集,若二者具有相同的祖先和后代,则属于同一可达性等价类,否则不属于同一可达性等价类。最后,将所有的可达性等价类构成的集合输出。
算法3 PSP算法。
输入 祖先集和后代集;
输出 可达性等价类集。
1)确定分段大小S;
2)遍历顶点,对每个顶点分别统计其祖先集和后代集在每个分段内的个数;
3)遍历顶点对,若顶点对的统计值相同,则进一步比较顶点对的祖先集和后代集是否相同,否则无需进一步比较;
4)具有相同祖先集和后代集的顶点构成一个可达性等价类,不存在相同祖先集和后代集的顶点单独作为一个可达性等价类。
例4 有顶点A、B、…、I,设A 的祖先集为{C,D,E,G,H},B 的祖先集为{C,D,G,H,I},为比较A、B 的祖先集,传统方法需对两个集合取交集得{C,D,G,H},其交集元素个数小于原集合元素个数,因此不等价。PSP 算法考虑将顶点进行分段,以分段大小S=3 为例,此时各分段的顶点为{A,B,C}、{D,E,F}、{G,H,I},对A的祖先集统计结果为[1,2,2],B的统计结果为[1,1,3],对A、B的统计结果进行比较,若不同,可以断言A、B 的祖先集不同,无需进行精细比较;若A 的祖先集不变,B的祖先集改为{C,D,F,G,I},则B的统计结果变为[1,2,2],A、B 的统计结果一致,需采用传统方法进一步进行精细比较。
在顶点对的比较过程中,QPGC 算法每次都进行精细比较,设其用时为f(|V|),由于PSP算法先对长度为的统计值进行比较,如果统计值相同,再进行精细比较,因此,其用时可表示为f(L+p ⋅|V|),其中p 为进行精细比较的概率,则PSP 算法与QPGC 算法的用时比为若f 为线性函数,则用时比为
3 实验结果与分析
3.1 实验数据集与环境
本文使用了6 组实验数据集,数据集名称、大小、来源及在文中的简称如表1所示;实验环境配置如表2所示。
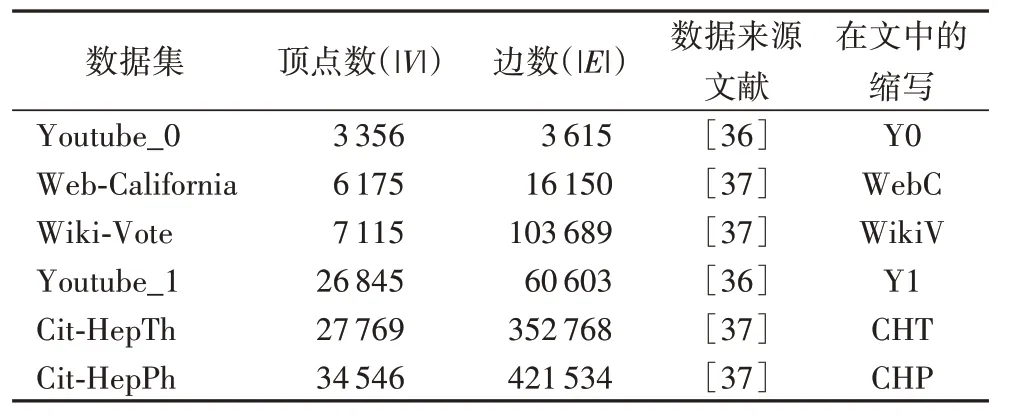
表1 实验数据集Tab.1 Experimental datasets
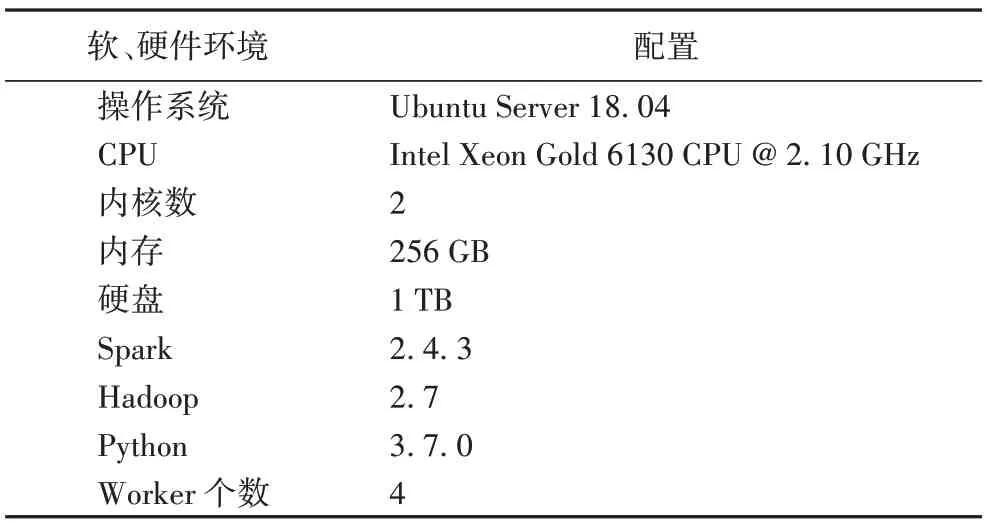
表2 实验环境配置表Tab.2 Configuration of experimental environment
3.2 实验结果与分析
进行2 组实验来验证本文提出的可达性查询保持图压缩策略的可行性和高效性。第1 组实验对改进的祖先后代集求解算法TSB和AGGB与原始算法QPGC的性能进行了对比;第2 组实验对改进的可达性等价类求解算法PSP 和原始算法QPGC 的性能进行了对比,并对分段大小S 与PSP 算法性能的关系进行了实验分析。接下来,实验分析了PSP 算法由分段统计引发的额外存储空间的消耗。最后,对比了QPGC 算法和本文算法的整体耗时。为保证实验结果的稳定性,本文所有实验结果均为5次实验取平均值。
本文方法与QPGC 算法采用相同的压缩理念,根据可达性等价顶点集具有相同的可达性关系,对其进行压缩,得到的压缩图与原图是可达性等价的,压缩图中可达性查询的结果就是原图上的结果。本文提出的压缩策略与QPGC 算法得到的压缩结果完全一致,压缩效果如表3所示。文献[30]第6章中对不同数据集应用可达性查询保持图压缩算法达到的效果进行了较为详细的对比和分析,本文不再赘述。
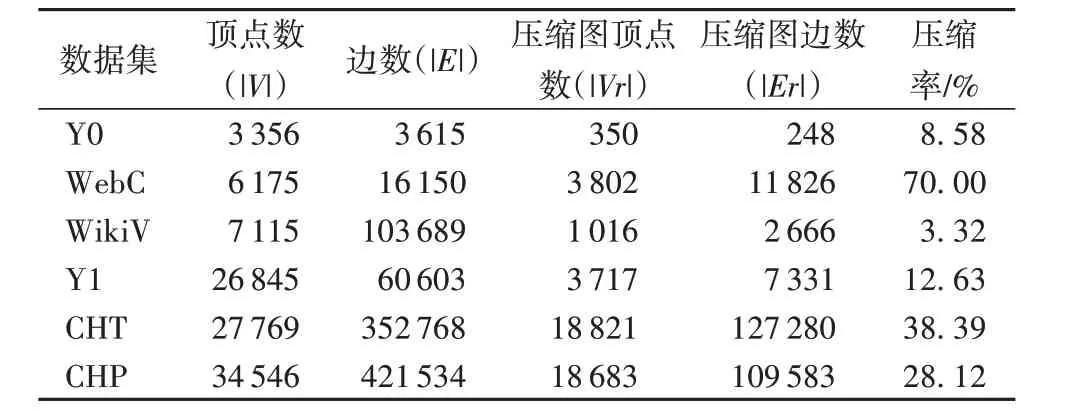
表3 本文算法的压缩率Tab.3 Compression ratio of the proposed algorithm
3.2.1 祖先后代集求解算法性能对比实验
本文算法相对QPGC 算法的加速比如表4 所示。从表中可以看出,与QPGC 算法相比,本文提出的两种算法执行时间显著减少,其中TSB 平均加速94.22%,AGGB 平均加速90.00%。
TSB 和AGGB 间互有优劣。在数据集Y0 上,AGGB 执行速度较TSB 快;在数据集WebC 和WikiV 上,TSB 执行速度较AGGB 略快;在数据集CHT 和CHP 上,AGGB 较TSB 执行速度慢近50%,这是因为这两个数据集为引文数据集,其数据图中路径较长,聚合运算次数较多。
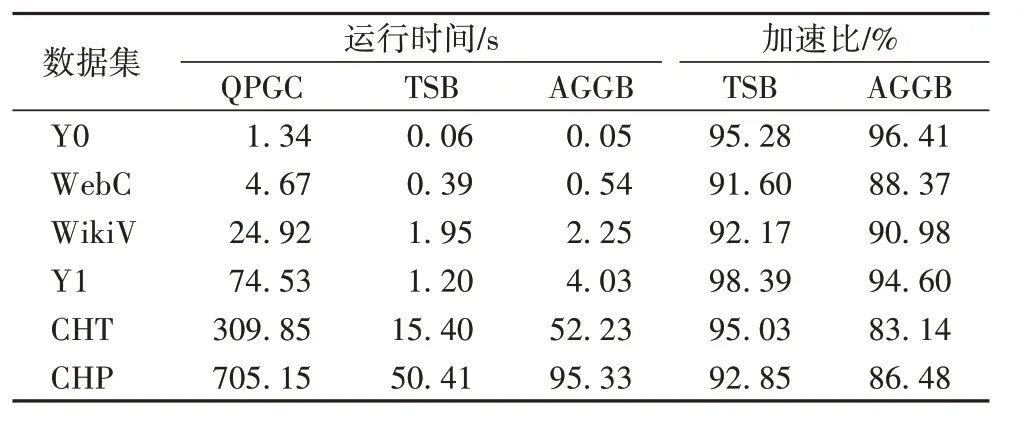
表4 TSB、AGGB与QPGC三种算法的性能对比Tab.4 Performance comparison of TSB,AGGB and QPGC
TSB、AGGB 和QPGC 算法的执行时间随数据集规模变化的趋势如图3 所示。从图中可以看出,随着数据集规模的扩大,三种算法求解祖先集与后代集过程的执行时间均呈现上升趋势,其中QPGC 算法受数据集规模影响较大,上升速度较快,TSB和AGGB受数据集规模影响较小,上升速度缓慢。
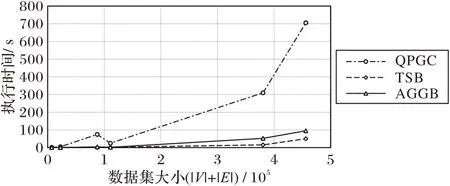
图3 三种算法执行时间随数据集规模变化趋势Fig.3 Trend of the execution time of three algorithms with increasing dataset
最后对TSB、AGGB 和QPGC 算法求解祖先后代集的存储开销进行对比。由于3 种算法的输入输出一致,仅考虑中间变量的存储占用情况,如表5 所示。从表中可以看出,与QPGC 算法相比,TSB 中间变量内存使用明显增大,但是其值在可以接受的范围内(KB 级),而AGGB 仅使用固定的中间变量,内存占用较小且不变。因此,本文方法在大数据上较QPGC算法有更优异的表现。
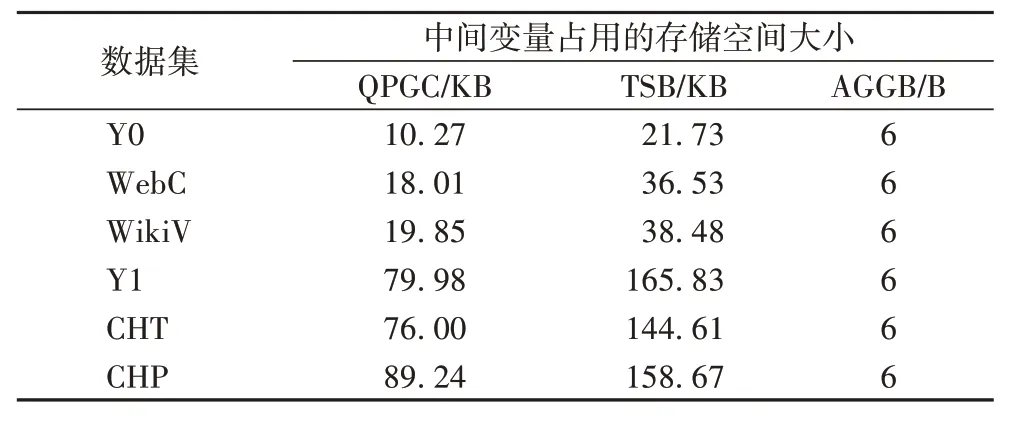
表5 三种算法中间变量的存储占用对比Tab.5 Comparison of memory usage of intermediate variables of three algorithms
3.2.2 可达性等价类求解算法性能对比实验
首先对PSP 算法在不同分段大小S 取值下相对QPGC 算法的加速效果进行对比。
取分段大小S为5、10、50、100、500、1 000、2 000,PSP算法相对QPGC 算法的加速比如图4 所示。可以看出,不同的S 取值下,PSP 算法较QPGC 算法计算速度均有明显提升,显著提高了可达性等价类的计算速度,除Y0 数据集外,加速效果均在70%以上,其中对数据集WebC、CHT 和CHP,加速效果达到了90%以上。

图4 PSP算法相对QPGC算法的加速比Fig.4 Speedup of PSP algorithm compared to QPGC algorithm
接下来,对PSP 算法在不同数据集上较QPGC 算法的加速效果进行分析。
通过分析对比,PSP 算法与QPGC 算法的用时比(用时比与加速比的和为1)与数据集压缩后得到的等价压缩图的点边比间的关系如图5 所示,可以看出,两种算法的用时比与压缩图的点边比呈正相关关系,因此,精细比较的概率p 与压缩图的点边比呈正相关关系。
此外,分段大小S 也会影响p 的取值,随着S 取值的变化,p 也会发生变化,从而导致PSP 算法较QPGC 算法的加速比发生变化。从图4 中可以看出,当S 取值为100 时,加速比基本达到最高值,此后,WikiV 数据集上加速比开始下降,其他数据集上加速比有极小幅度的上升。鉴于此,本文对S 取值在[5,200]区间内加速比的变化做了进一步研究,结果如图6 所示。从图中可以看出,当S取值很小时,加速比较小;S在[50,100]区间内,加速比基本达到最高值;此后,加速比有一定的波动,并逐渐开始下降。这是因为,如果S 取值过小,分段数将增大,粗粒度比较的计算成本升高;如果S 取值过大,将有更多的顶点被误分为备选可达性等价顶点集,从而导致精细比较次数增多,提高了计算成本。另外,加速比的变化不是平滑的,具有一定的波动性,这与分段统计过程中,分段大小、编号顺序、祖先后代分布均有一定的关系。
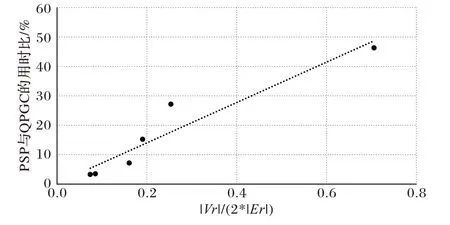
图5 用时比与数据集压缩后得到的等价压缩图的点边比间的关系Fig.5 Relationship between time cost ratio and point-edge ratio of equivalent compression graph obtained after data set compression
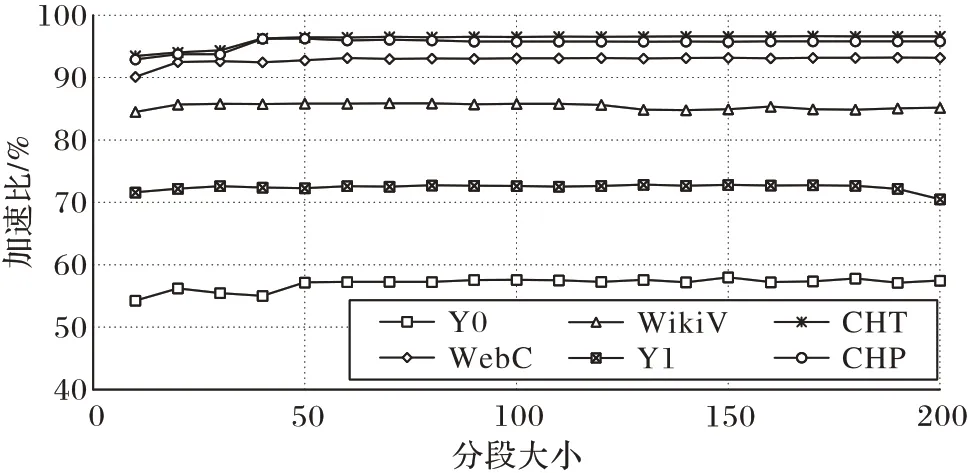
图6 PSP算法相对QPGC算法加速比与分段大小S的关系Fig.6 Relationship between speedup of PSP algorithm compared to QPGC algorithm and segment size S
另一方面,分段统计带来了额外的存储开销,且空间占用与S 的大小有关,如表6 所示。可以看出,当S 取值较小时,存储空间占用较大,且随着数据集的增大,存储空间也在增大。当S 取1 000 时,CHT 和CHP 数据集上存储空间占用不足1 MB,是当前硬件条件下可以接受的。
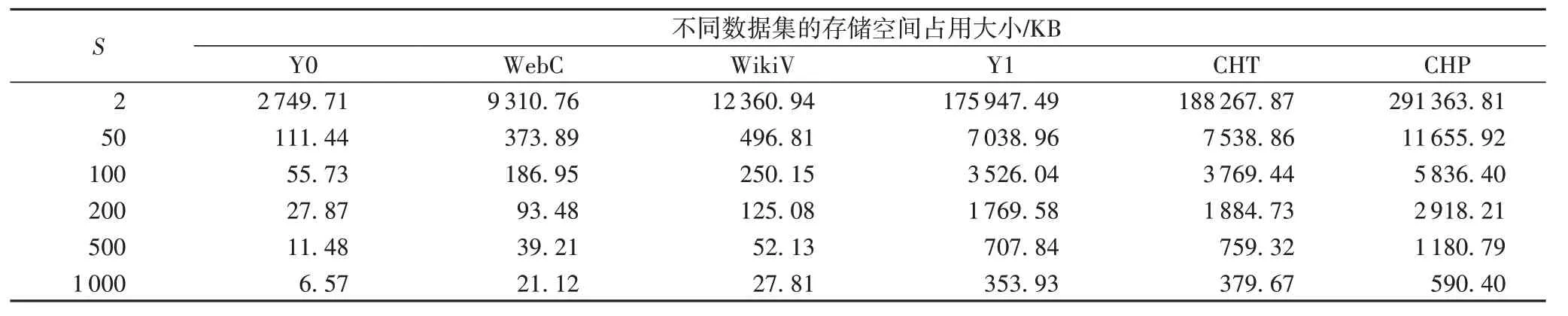
表6 不同分段大小S下的存储空间占用Tab.6 Memory usage under different segment size S
综上所述,S 取值过小,存储空间占用会显著增大,S 取值过大,精细比较的概率p随之增大,因此,分段大小S取值应适中,并结合具体应用环境进行分析,达成时间和空间的协调。例如,在应用中,若存储空间较为充足,则可适当的减小S,以空间换时间,否则应适当增大S。
接下来,对两个阶段的执行时间占比进行统计分析。以Y0 和WikiV 数据集为例,取分段大小S=100,求解祖先后代集阶段(第1 阶段)和求解可达性等价类阶段(第2 阶段)的占比如图7 所示。从图中可以看出,第2 阶段用时所占比重更大。
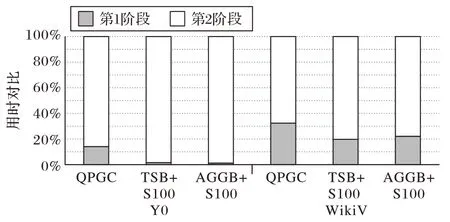
图7 两阶段执行时间占比Fig.7 Proportion of execution time in two stages
最后,在6 组数据集上分别应用TSB+S100、AGGB+S100和QPGC 算法,总体用时对比如表7 所示。从表中可以看出,本文提出的TSB 和AGGB 配合PSP 算法,时间性能提升显著,随着数据量的增大,性能提升近28倍。
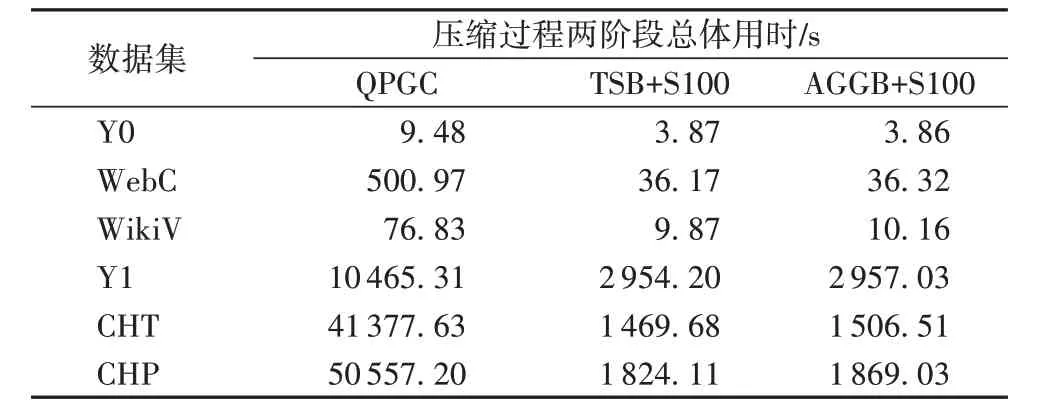
表7 总体用时对比Tab.7 Total time cost comparison
4 结语
本文提出了一种低冗余计算的可达性查询保持图压缩策略。其中:TSB 通过拓扑排序确定祖先后代集求解顺序,避免了重复计算;AGGB 可在不超过最长路径长度次数的聚合运算内完成求解,对最长路径长度较小的数据图有较好的效果;PSP 算法预分段统计BFS 结果集,利用统计值对匹配过程剪枝,剪除了大量的不必要匹配。实验结果表明,本文提出的可达性查询保持图压缩策略,较现有方法显著减少了冗余计算,在不同的数据集上均取得了较好的加速效果。因此,本文策略提高了压缩速度,冗余计算少,是可行且高效的。
下一步,我们将研究大规模图数据可达性查询的应答策略,从查询求解的角度减少应答时间,提高应答速度。
