基于线性分配的难负样本挖掘度量学习

傅泰铭，陈 燕，李陶深

（广西大学计算机与电子信息学院，南宁530004）

0 引言

近年来，卷积神经网络（Convolutional Neural Network，CNN）已经被证实了在计算机视觉的多个应用领域能取得相当优越的性能，如目标检测、人脸识别、图像分类等。CNN 在经过良好的训练后具有十分强大的表达能力，甚至能用来区分未被训练的任务。

以图像分类的方式完成鲸鱼身份的自动标注存在局限性。因为在训练分类器时，分类器通过提取正负样本的特征差异实现分类图像，而鲸鱼个体尾巴特征差异十分微小，并且难以保证每个类别都有足够的样本用于学习。

本文使用相似性度量学习（Metric Learning）［1］根据鲸鱼的尾巴特征来识别鲸鱼的属类。利用CNN 对图像进行特征提取后，通过对比特征编码之间的距离度量，利用基于线性分配的难负样本挖掘方法，不同于基于抑制简单样本的难例挖掘，线性分配问题（Linear Assignment Problem，LAP）算法可以根据模型的学习情况动态地构筑训练对，并通过调整样本采样顺序的方式使模型得到充分训练。

1 相关工作

传统的CNN 对每个个体都需要大量的标记数据，对每一个新发现的个体都需要重新训练网络。1993 年，Bromley 等［2］针对这一问题引入了一种合适的神经网络架构——孪生神经网络（Siamese Neural Network，SNN），该网络学习检测两个输入图像是否相似或不同的。经过训练后，SNN 只需要一个带有标签的输入图像，以便准确地重新识别第二个输入图像是否同一个人的，在人脸识别领域得到广泛应用［3-4］。在实践中，人们会训练SNN 来学习一个物种的相似性，并利用已知的既定事实来比较不同的个体。2015 年，Schroff 等［5］推出了基于孪生网络的网络架构FaceNet，该架构在YouTube 人脸数据集中拥有最高的准确率，曾在top-1 准确率上达到95.12%。并且出现了许多行人重识别（Person Re-identification，ReID）和SNN 的改进模型［6-9］，尤其在目标追踪领域，SNN 的应用十分广泛［10-12］。

SNN 属于模板匹配算法，任何模板匹配算法对采样策略都十分敏感，特别是存在样本不平衡时，而样本不平衡问题广泛存在于大多数任务中。2011年，Barua等［13］提出合成少数类过采样（Synthetic Minority Oversampling Technique，SMOTE），通过对少数类样本进行分析并根据少数类样本人工合成新样本添加到新数据集中对样本进行平衡。2016 年，Shrivastava等［14］提出了难例挖掘（Online Hard Example Mining，OHEM），能够对简单样本进行抑制，使得训练过程更加高效。2017年，Lin 等［15］提出焦点损失（Focal Loss，FL），通过引入两个新的超参数，计算损失时为不同的样本分配不同权重，大幅缓解了样本类别不平衡问题，并将One-Stage 目标检测模型的性能提高至顶尖水准。

线性分配问题是基本的组合优化问题。通过利用线性分配算法为模型挑选样本对有助于加速模板匹配类模型的收敛。本文设计了一种新的度量计算方式，并使用基于线性分配的难负样本挖掘，在具有少数类别样本的鲸鱼尾巴数据集和CUB-200-2011数据集上取得了良好的识别效果。

2 SNN模型

本文所使用的SNN 模型具有两部分：第一部分为分支模型，第二部分为头模型。整体结构如图1 所示。分支模型是对常规卷积神经网络框架取消最后的池化（Pooling）层和全连接（Full Connected，FC）层，因此从分支模型将会得到一个从图像进行提取的特征向量编码。以卷积密集网络DenseNet［8］为例，DenseNet121 将输出1 024 维的特征向量。使用一对具有共享权重的特征提取卷积网络分别对输入样本对进行特征提取，得到一对图像特征向量。头模型对特征向量进行度量距离计算，因此头模型也称为距离层（Distance Layer），输出相似度函数值（通过Sigmoid激活）。

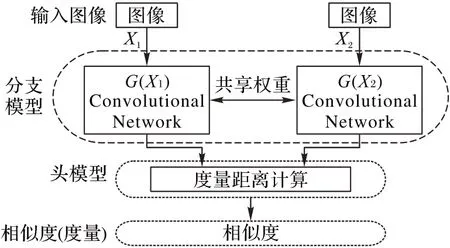
图1 本文算法整体结构Fig.1 Overall structure of the proposed algorithm

通过头模型对分支模型提取出的一对特征向量计算距离，典型的方法是使用欧氏距离度量，定义为：

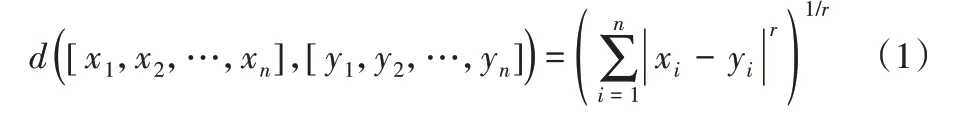
但是有以下原因使得本文尝试不同的方法来计算距离：

1）欧氏距离度量将两个值为0 的特征视为完全匹配，而两个不相等的正值确实为良好匹配（意味着不完全匹配）。然而，在正面（position）特征中比在负面（negative）特征中有更多的正面信号，特别是在线性整流函数（Rectified Linear Unit，ReLU）激活中，这个概念会被距离度量丢弃。

2）欧氏距离度量不提供特征之间的负相关。

因此本文在距离层设计一种新的方法通过一个小型神经网络来学习和计算特征之间的度量距离：

输入 一对特征向量x和y；

输出 距离度量D。

1）将通过计算式（2）～（5）得到的向量拼接为一个长度为4×n的一维矩阵lambda，n为特征向量的长度。

2）将一维矩阵lambda 传递给一个小型的神经网络层，该网络可以学习如何在匹配的零和接近的非零值之间权衡。每个特征使用相同的神经网络，具有相同的权值。网络结构为2 层卷积层，之后将向量展开为一维后输入全连接层，全连接层输出同类的概率，该输出是转换后的特征的加权和，带有Sigmoid激活。头结构如图2所示。

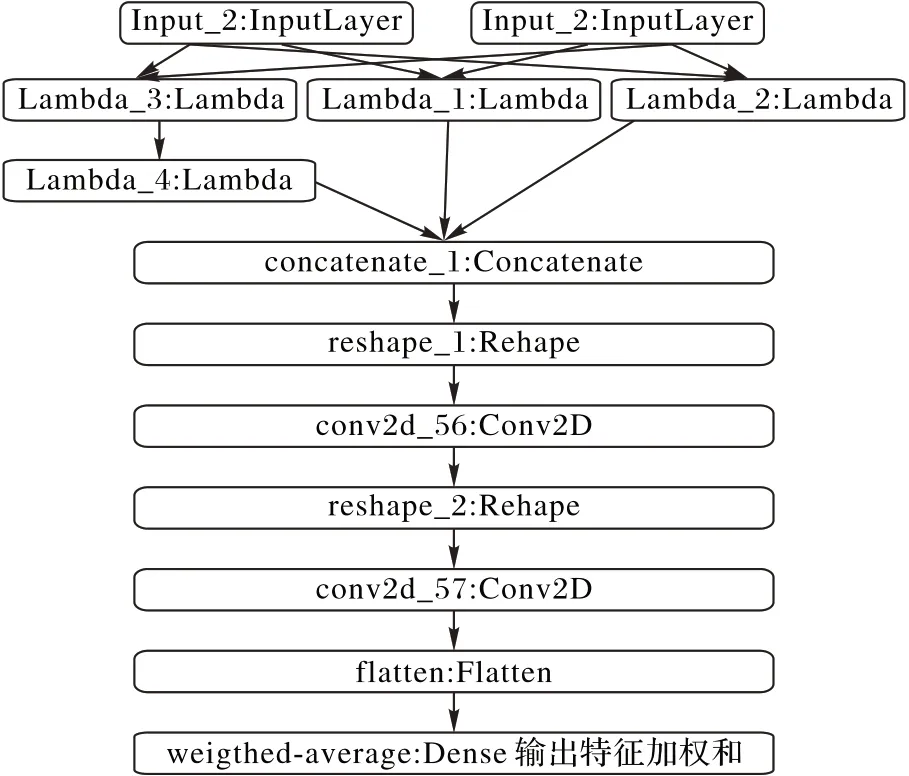
图2 头模型结构Fig.2 Head model structure

3 对抗性训练

由于模型的表达性能在训练期间会得到提高，因此有必要随着训练的进行提供更困难的训练样本对。对于任何随机图像对，相对容易预测它们是否匹配鲸鱼，但是当涉及到更困难的样本时，该模型将很难作出决定。

在训练开始时，通过随机抽样匹配（正）和不匹配（负）对来为模型提供更简单的案例。这是因为若训练开始就将困难样本输入模型，收敛会十分困难。

因此随着训练的进行，开始输入更加困难的负对。由于来自不同类别的任何两只鲸鱼可以形成负对，并且只有来自同一类别的鲸鱼可以形成正对，因此训练期间负对比正对数量更多。由于这种限制，在模型中只为不匹配的鲸鱼形成负对，并对正对仅使用随机抽样。

3.1 线性分配

用线性分配问题（LAP）算法来解决负对的选择问题，任务分配问题是在加权二分图中寻找最大（或最小）加权匹配的问题。

利用LAP对样本进行采样从而构筑训练批次的过程可以简化为以下过程，以一个5×5度量分数矩阵为例，矩阵中的元素代表一对训练对的距离度量，通过特征提取得到如下分数矩阵：

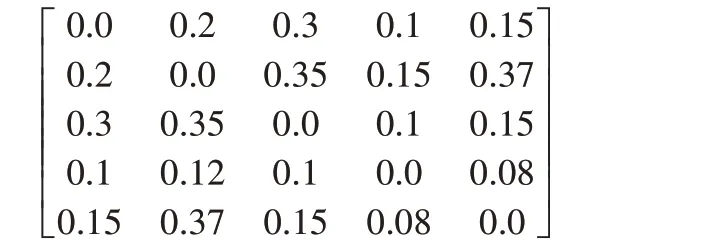
由于算法只挑选负对，所以设对角元素为∞。得到如下分数矩阵：

对于每次迭代，LAP 将输出一个由5 个负对组成的解，当模型训练完这些负对后，将分数矩阵上对应的坐标和其对称坐标设为无穷，进入下一次迭代并再次使用LAP 得到负对用于训练。

在经过一段时间的训练后，矩阵会被消耗殆尽，此时通过重新运行模型再次生产新的分数矩阵。

3.2 基于线性分配的负样本挖掘算法

利用训练后的模型计算所有样本对的距离度量分数矩阵作为矩阵T，其中每个元素Tij是该模型对图像i 和图像j 是否同类的预测概率。

输入 分数矩阵T；

输出 用于训练的负对。

1）将T 中所有值变为负数，即(-1)×T。因为LAP 会采样度量差异最小的样本对，因此将度量分数取反从而采样度量距离最大的样本对。

2）查找T 中与匹配对对应的所有值，将它们的值设置为较大正数（例如10 000），将已训练的样本对过滤。

3）对于矩阵T 中的每个值加上K×x，其中x(0 ≤x ≤1)为随机值，K 在训练过程中从1 000 逐渐减小为需要的较小值（例如0.05），这是因为如果不使用K（即K=0），模型将始终挖掘最困难的例子，这是不理想的，并且在训练的初期限制算法为模型提供随机样本对，以形成模型的初步识别能力，在经过一定次数的迭代后逐渐转变为LAP 策略，因此整个过程是一个随机采样慢慢过渡到LAP采样的过程。

4）使用LAP 来计算每一行i，从对应的列j 中计算对应的对，使得总的代价（所有行的代价求和）最小。然后将使用选定的(i，j)对进行下一阶段的训练。

3.3 正对匹配策略

对于正对，使用最简单的随机匹配算法，同时计算其错排（derangements）。错排的定义为：考虑一个有n 个元素的排列，若一个排列中所有的元素都不在自己原来的位置上，那么这样的排列就称为原排列的一个错排。

这是为了保证没有图像会与自身配对，并且每个图像只会使用一次来形成样本对。

基于LAP的负样本挖掘利用负对的相似性度量为模型提供更加困难的样本对，而不是输入随机的样本对，根据分数矩阵动态地调整训练样本的输入过程，并保证简单的样本对也能得到训练，因此加快了模型的收敛。

4 实验过程与结果分析

本文实验均在Intel Core i7-8700K@3.70 GHz CPU，16 GB 内存，GPU 为Nvidia GTX 1080的平台上实现，操作系统为Windows 10（64 bit），代码在深度学习PyTorch环境下实现。

损失函数使用二元交叉熵（Binary Cross Entropy，BCE）：

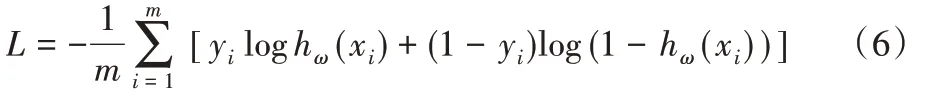
其中：m 为样本数，yi为第i 个样本标签，xi为第i 个样本的特征。

评价指标采用mAP@5（mean Average Precision@5），定义为：

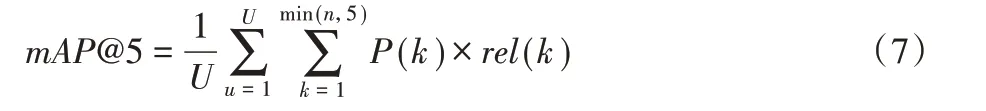
其中：U 是图像的数量；P(k)是在截止点k 处的精度（Precision）；n 是每张图片预测的数量；rel(k)是一个指示函数，如果第k级的项是相关的（正确的）标签，则为1，否则为0。精度Precision的定义如下：

其中：TP（True Positive）表示正确分类的正例数量，FP（False Positive）表示错误分类的正例数量。

4.1 数据集

本文采用的数据集为鲸尾数据集和细粒度分类数据集CUBU-200-201。其中，鲸尾数据集的类别十分不平衡，共有25 361 张图像用于训练，7 960 张图像用于测试。该数据集中大多数是垂直拍摄的鲸尾图像，如图3，每个图像都具有较高的分辨率，例如1 560×600，但是有一些图像较为异常，尺寸非常扭曲，比如尺寸失真、拍摄角度不正确以及图像不清晰等。

通过对鲸尾数据集的标签分布进行统计，发现其标签分布十分不均衡：在25 361张鲸鱼图像中，总共有5 005种鲸鱼，然而其中有9 664个属于未知类别，在该类别中的鲸鱼具有不同个体的特征，因此最简单有效的办法是将所有未知类别样本从训练集剔除，只对剩余的5 004 种鲸鱼进行训练，于是得到有用的图像数量有15 697 张，然而在这其中的标签分布也十分不均衡。其中新鲸鱼类别的图像后续将作为模型未见过的样本进行验证。

根据统计，5 004个类别中有大约2 000个类别仅有1张图像，且有大约1 250 个类别仅有2 张图像。同时模型需要捕捉鲸鱼尾巴划痕图案的微小特征差异来对鲸鱼身份进行辨认，这对模型的性能有一定要求。

图3 数据集中部分垂直拍摄的鲸尾图像Fig.3 Some images of whale tail taken vertically in the dataset

4.2 实验参数

使用Adam 优化器（optimizer），采用动态学习率，初始取值为64×10-5，之后每100 个epoch 减半，l2 正则化参数设为2×10-4；LAP 中的K 值初始为1 000，10 个epoch 后设为100，150 个epoch 后设为1，之后每50 个epoch 减半，总计训练200个epoch。

模型编码器使用在ImageNet［16］预训练的权重来初始化网络参数。

头部模型结构及参数如表1所示，其中“”表示输入层，没有被连接对象。

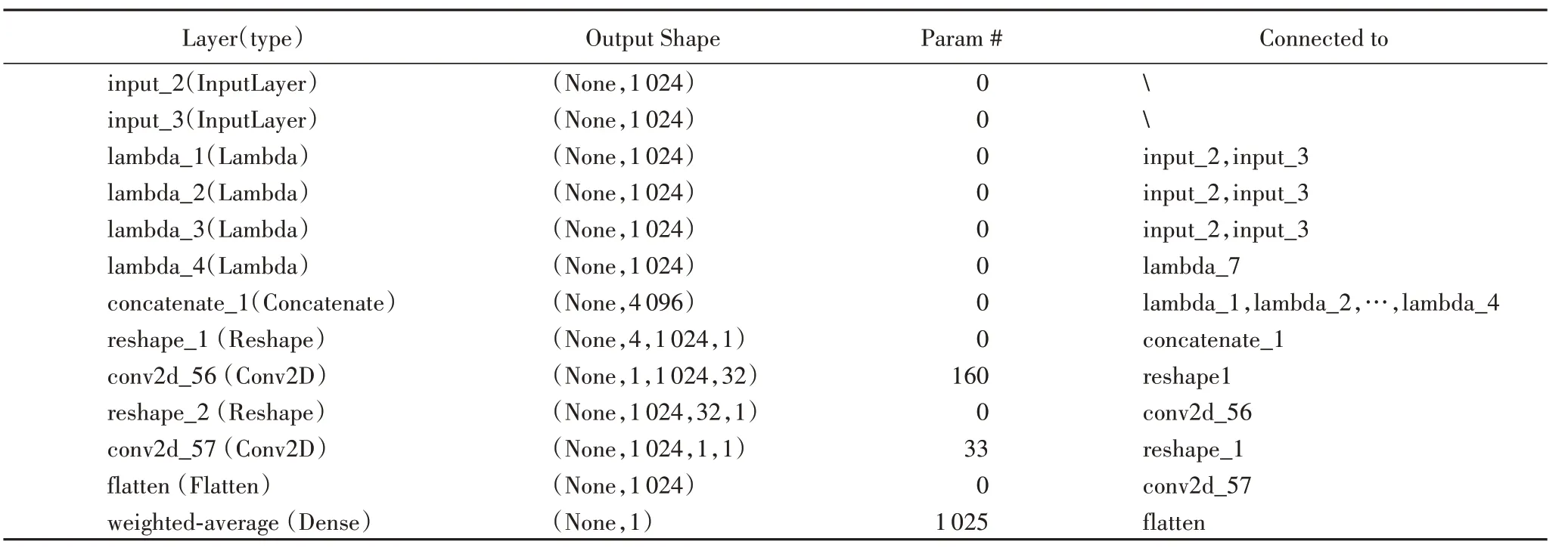
表1 头部模型结构及参数Tab.1 Structure and parameters of head model

4.3 实验结果及对比

使用4 种采样策略进行对比，并且均使用本文提出的度量计算方式：

1）SNN：随机挑选样本对；

2）SNN with OHEM：使用OHEM进行样本对挖掘；

3）SNN with FL：使用焦点损失抑制简单样本对；

4）SNN with LAP：通过LAP算法挖掘样本对。

得到的对比结果如表2 所示，而不同采样策略下的指标变化如图4所示。

其中：焦点损失采用的超参数为γ=2，α=0.25；难例挖掘采用正负样本比例为1∶3。

OHEM 的问题在于放弃了大量简单样本，在持续训练中容易导致模型的学习偏差。

焦点损失的问题在于数据集的样本之间具有较高的相似性，仅通过损失难以区分样本的难度。

结果表明，对于模板匹配模型，基于LAP的难例挖掘采样策略逐渐为模型提供更困难的样本对，而不是所有样本对的随机子集，使得模型能更有效地进行学习。

同时由于每次训练重新生成分数矩阵以挑选负对，因此会导致指标和损失函数的曲线呈锯齿状。

通过训练不同的编码器得到结果如表3 和图5 所示。图5中，X轴为epoch，Y轴为损失数值，同样由于生成分数矩阵的原因，曲线非常陡峭，但总体仍处于收敛状态。

由训练指标和损失函数的对比结果可知，本文算法在具有少样本、未知样本特点的细粒度图像分类问题上具有良好的性能，根据表2和表3可知，相比原型SNN，本文算法在指标上取得了良好的性能提升；同时解码器对算法的性能也有较大影响，通过选择不同的解码器对结果具有不同影响。

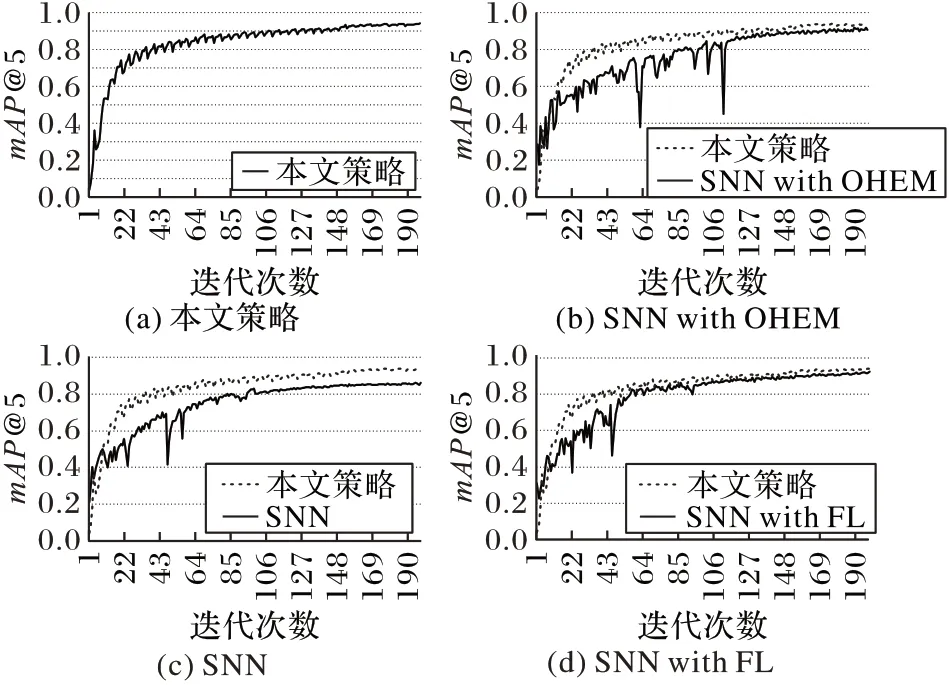
图4 不同采样策略的mAP@5变化Fig.4 mAP@5 change of different sampling strategies

表2 不同采样策略的mAP@5对比（DenseNet121编码器）Tab.2 Comparison of mAP@5 by different sampling strategies（DenseNet121 encoder）

模型中间层的可视化如图6 所示，由模型识别出的测试数据匹配对结果如图7所示。

表3 不同编码器的mAP@5对比Tab.3 Comparison of mAP@5 by different encoders

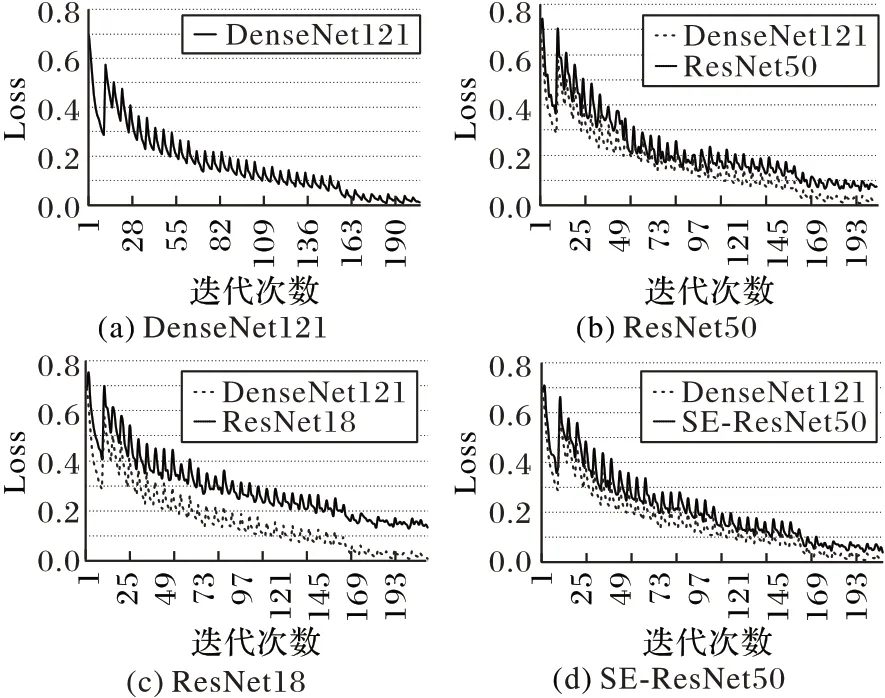
图5 不同编码器下的损失函数变化Fig.5 Loss function change in different encoders

CUB-200-2011 是一个细粒度分类数据集，在CUB-200-2011 以 召 回 率Recall@1、Recall@2、Recall@4、Recall@8、Recall@16、Recall@32 为指标得到的结果如表4 所示。由表4可以看出，直接对整个数据集使用难例挖掘难以取得指标上的提升。而利用线性分配采样策略在Recall@1 上对比随机采样策略，取得了4.2 个百分点的指标提升，说明线性分配采样策略对于实用性具有良好的提升作用；并且在Recall@4 上具有最高的指标提升（6.3个百分点）。

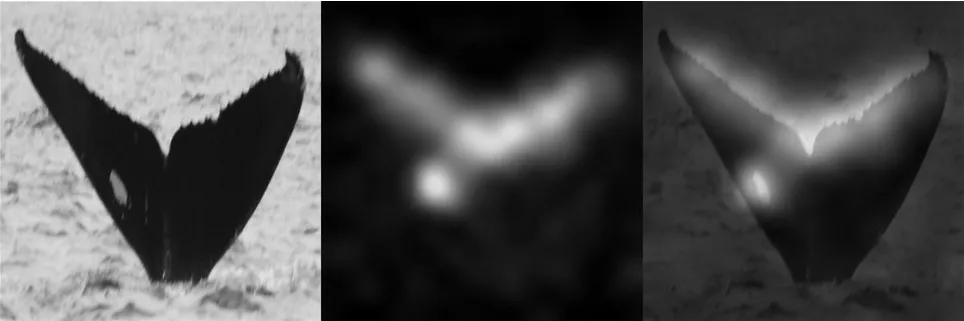
图6 输入样本的特征激活可视化热图Fig.6 Heatmap of visualization of input sample features activation

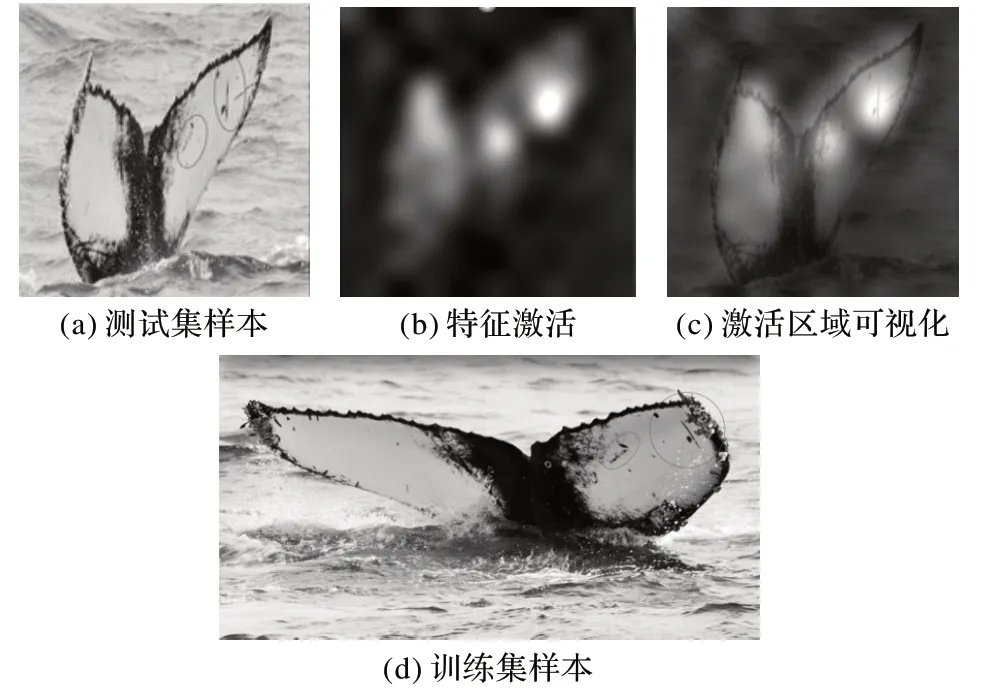
图7 匹配结果Fig.7 Matching results

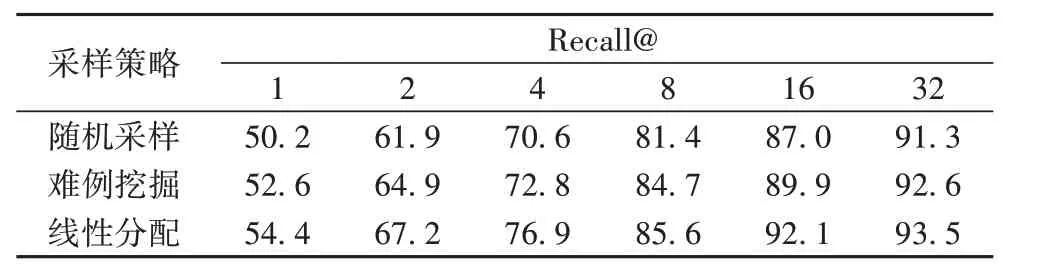
表4 在CUB-200-2011数据集上的召回率对比 单位：%Tab.4 Comparison of recall on CUB-200-2011 dataset unit：%

5 结语

本文针对深度学习中的细粒度识别和一次学习问题，对孪生神经网络的训练过程和距离度量进行改进，并在一个具有少样本、未知样本特点的细粒度鲸鱼图像分类数据集和细粒度分类数据集CUB-200-2011 上取得了良好效果。但本文方法仍有改进之处，如利用LAP 进行难负样本挖掘的耗时较长，在其后生成的热图也表明图片中的噪声（例如背景中的飞鸟）会让模型错误地提取特征。但就总体而言，模型可以正确地提取图像的细粒度特征，因此大多数图像可以得到有效识别。同时利用本文方法需要额外花费算力生成分数矩阵，并且计算LAP也需要一定计算量，因此会相对耗时，后续的改进工作会围绕速度方面进行。