ARMA模型在LNG价格预测中的应用

【摘要】液化天然气（LNG），一种污染程度低、释放热量大、被认为是一种极为清洁的能源，越来越受到人们的关注。在我国天然气市场条件下，对LNG价格进行预测可以为天然气市场参与者提供价格参考依据。本文运用时间序列分析原理对我国LNG价格进行预测，使用计量经济学软件Eviews分析，对数据进行时序图绘制、平稳性检验、数据平稳化处理、模型识别、参数估计、模型检验，建立时间序列ARMA模型对LNG未来价格做出短期预测。

【关键词】LNG  时间序列  价格  ARMA模型

一、引言

在我国天然气市场条件下，LNG价格受到很大的关注，对其价格进行预测显得尤为重要，一方面不但为天然气市场参与者提供了一定的价格依据，使其提前做好相关决策，减少不必要的损失，另一方面也有利于天然气市场的持续稳定健康发展。

由于长期价格预测相对于短期预测而言，时间跨度太大，不能达到很好的预测效果，而且不确定性也会随着预测时间的增加而增大，这使得预测难度变大，预测精度不高，而时间序列正好满足中短期预测这一目标。所以，本文在基于2019年1月1日到至2019年9月9日我国LNG出厂价相关数据，通过对已有研究成果的分析，首先提出本文的研究意义，随之介绍相关模型的理论知识，然后以LNG出厂價作为时间序列分析的数据，对该序列建立ARMA模型，并对模型进行有效性检验，进而对LNG出厂价进行短期预测。

二、ARMA模型理论知识概述

（一）ARMA模型

时间序列模型是LNG价格模型的重要部分，LNG价格形成的时间序列前后时间段具有较强的关联性，时间序列法可以根据这种关联性建立相应模型，以此预测LNG未来的价格，ARMA模型即为时间序列模型之一。

ARMA模型也即自回归移动平均模型，由Box-Jenkins创立，也称B-J方法，是一种精度较高的短期预测方法。此模型是最常用的拟合平稳时间序列的随机模型，因此在建立ARMA模型之前进行序列的平稳性检验，若为非平稳，需经差分处理，再对新的平稳序列建立ARMA（p，q）模型。ARMA模型是由MA模型和AR模型，也即滑动平均模型和自回归模型， “组合”而成，数学模型分为： AR模型、MA模型以及ARMA模型。

AR（p）模型：Xt=ч1Xt-1+ч2Xt-2+…+чpXt-p+εt   （1）

其中，p为阶数，ч1，ч2…чp为待定系数其算子形式为：

ч（B）Xt=εt    （2）

其中， εt为均值为零的白噪声序列

MA（q）模型：

Xt=εt-θ1εt-1-θ2εt-2-…-θqεt-q  （3）

其中q为阶数，θ1，θ2，…，θ1q为待定系数，其算子形式为：

Xt=θ（B）εt   （4）

ARMA（p，q）模型：

Xt=ч1Xt-1+ч2Xt-2+…+чpXt-p+εt-θ1εt-1-θ2εt-2-…-θqεt-q

（5）

其算子形式为：

ч（B）Xt=θ（B）θt    （6）

其中，θ（B）=1-θ1B-θ2B2-…-θQBq，ч（B）=1-ч1B-ч2B2-…-чpBp，B为滞后算子。

由此可见，AR（P）模型和MA（q）是ARMA（p，q）的两种特例，即AR（P）模型是q=0时的ARMA（p，q）模型，MA（q）模型时p=0时的ARMA（p，q）模型。

（二）平稳时间序列

平稳时间序列包含严平稳和弱平稳时间序列。严平稳时间序列要求随着时间的不断变化，序列的一切性质均不会改变，也即是在判断一个时间序列是否为平稳时条件较苛刻，平稳性的结果也较为完美。然而，实际能够达到严平稳相应条件的序列并不多，且计算也较为困难。所以，严平稳时间序列只是存在于理论定义基础上，弱平稳时间序列才是实际问题中应用最多的，其均值、方差和协方差均不随时间t的推移而变化。弱平稳时间序列的条件为：第一，对一切的t，有E（ut）=u;第二，对一切的t，有Var（ut）=б2;第三，对一切的s和t，cov（ut， ut-s）= rs

三、时间序列ARMA模型在LNG价格中的定量分析

对于天然气市场参与者来说，LNG的价格显得尤为重要，提前了解LNG未来价格的趋势走向，能使他们提前做好决策，减少不必要的损失。本文通过建立LNG价格的ARMA模型，来预测短期LNG价格变化情况。以上海石油天然气交易中心2019年1月1日到2019年9月9日的LNG出厂价作为研究对象，分析过程通过Eviews10.0软件实现。

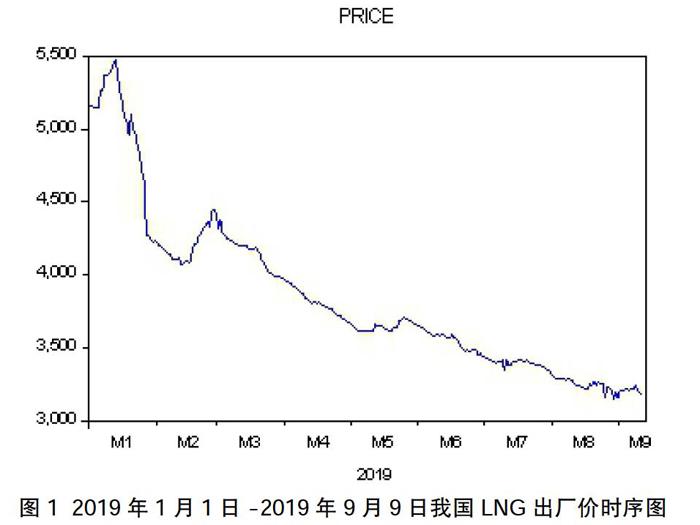
图 1为2019年1月1日至2019年9月9日我国LNG出厂价的时序图。从图中可看出，一月份LNG价格受气温的影响明显高于其他月份，之后随着温度的逐渐上升，价格呈现逐渐降低趋势。

（一）数据的平稳性检验

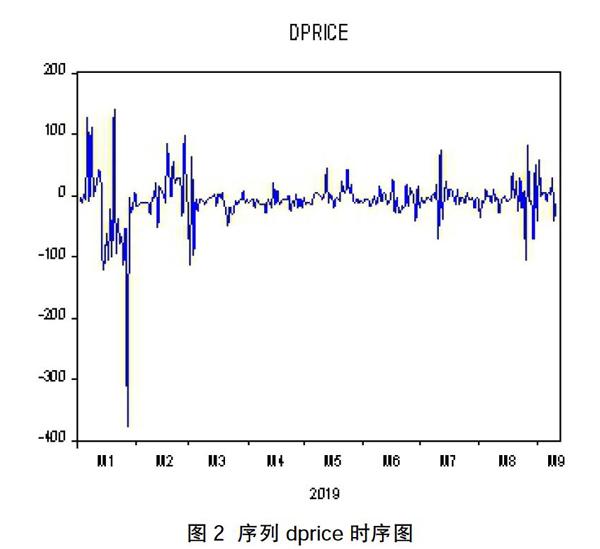
由图 1可以看出，价格序列PRICE逐渐降低，存在明显的趋势性，PRICE序列为非平稳时间序列，一阶差分形成新的序列DPRICE。图 2为序列DPRICE的时序图，序列均值与t无关，且各观察值围绕均值上下波动，且由表 1的 Unit Root Test可进一步确定，一阶差分后的序列呈现平稳性特征。

（二）模型的识别与参数估计

通过Eviews得到的序列DPRICE的自相关图（图 3）可以看出，p>2和q>2之后，样本ACF系数和PACF系数大多在标准差的两倍范围以内波动，且2阶到3阶的ACF系数和PACF系数骤降，呈现2阶截尾，根据B-J建模思想尝试用ARMA（2，2）模型进行序列的拟合。

利用Eviews进行各模型拟合结果如表 2：

结果表明，ARMA（2，2）的剩余平方和和AIC均较其余两模型小，因此，利用ARMA（2，2）模型对序列DPRICE进行拟合较为恰当，且拟合效果较好。使用最小二乘估计法，其表达式为：

DPRICEt=0.7089DPRICEt-2+εt+0.4086εt-2

（三）模型检验

两个参数的显著性检验结果表明：两参数的P值都小于等于0.0001，远小于显著性水平，即拒绝原假设，ARMA模型的两个参数均为显著，通过参数的显著性检验。

对于模型的适用性检验，也即残差序列的白噪声检验，可以看出，P值大多显著大于0.05，接受原假設，表明该模型通过了适用性检验，所以使用ARMA模型进行模拟预测是合适的。

（四）模型预测

利用ARMA（2，2）模型对2019年9月10日-2019年9月12日我国LNG出厂价进行预测。

四、结论与不足

本文的数据源于2019年1月1日至2019年9月9日我国LNG的出厂价，对该数据运用时间序列分析的方法，并使用计量经济学软件Eviews对LNG价格建立了ARMA模型，然后运用所建立的ARMA模型，对2019年9月10日至2019年9月12日的LNG出厂价进行了预测，预测值分别为3210、3177、3189，误差分别为0.66%、0.41%、2.53%。从模型的预测结果来看，拟合效果较好，且预测误差较小，在2.6%以内。预计接下来几天我国LNG出厂价会维持在3200左右这一水平，与前几日相比没有大幅度的波动。

虽然运用ARMA模型来预测LNG的价格有较好的预测效果，但是仍存在不足之处。首先，该模型只适用于预测短期内的序列值，若预测的时间过长，误差就会越来越大。其次，时间序列的期数也不能过少，再者模型的建立是假定其他因素不发生重大变动为前提。

参考文献：

[1]任行伟，温涛.农村居民储蓄率变动对城乡经济一体化发展的实际效应分析[J].经济视角（下），2011（09）：102-104.

[2]田天立.深市股价波动性分析[D].山东经济学院，2011.

[3]聂鹏.金融危机下人民币汇率的ARMA模型预期[J].西南金融，2011（03）：23-25.

[4]尹红伟，刘东进，顾华，徐小艳，李晓晨.大型LNG船用燃料罐研制[J].辽宁化工，2019，48（01）：80-82.

[5]康丹青. 基于深度学习的短时交通流预测方法研究[D].哈尔滨理工大学，2018.

[6]桂梅，刘莲花.基于ARIMA模型对海南省社会消费品零售总额的预测[J].数学的实践与认识，2017，47（03）：25-30.

[7]梅志娟.ARMA-GARCH模型的期货价格预测比较研究[J].经济研究导刊，2010（34）：73-74.

[8]谷国利.基于时间序列和神经网的风电场短期风速与功率预测研究[D].新疆大学，2010.

作者简介：殷青（1996-），女，汉族，四川，硕士研究生，研究方向：预测与决策。