基于幅值谱比对滤波的梁式桥实测冲击系数计算方法

刘晨光， 张连振， 高庆飞

(哈尔滨工业大学交通科学与工程学院，哈尔滨 150090)

冲击系数是反映桥梁动力响应特性的重要指标，是桥梁设计中的重要参数。由冲击系数在各国规范中的发展历程[1-2]可见，冲击系数的设计值是一个半经验半理论的取值，对冲击系数设计值的研究离不开现场试验数据的支持。同时，随着对桥梁检测与状态评估工作的重要性认识的逐渐提高，实测既有桥梁的冲击系数来评定桥梁的动力状态，已成为桥梁工作者的一项重要工作。因此，对冲击系数的实测检验方法进行进一步研究具有理论与实际的双重意义。

中国的桥梁设计规范中[3]，冲击系数定义为：在汽车通过桥梁的效应时间曲线上，由最大静效应位置处，量测得到的最大动效应与最大静效应的比值。在工程应用中，冲击系数的测量多基于动位移测试结果，所以在时间-位移曲线上精确地获取最大动、静位移是计算实测冲击系数的关键。其中，最大动位移的获取较为容易，只需在曲线上量取位移最大值；但是，最大静位移是动位移曲线中的隐含信息，需要对实测动位移信号进行分析处理，实现动、静位移分量分离后才能够获得。

文献[4]提供了一种通过直接的波峰-波谷平均法在位移时程曲线上计算最大静位移。此方法对理想信号具有较小效果，也是目前普遍采用的实测冲击系数计算方法。但在实际操作中，由于噪声等其他不确定因素的干扰，实测时程曲线往往不存在完美的明显峰值和谷值[5]，计算波峰、波谷的选择可能因人而异，导致无法做到对所有桥梁的稳定客观评价。

文献[6]提供了另一种通过车辆低速通过桥梁的跑车试验来获得准静态的桥梁位移曲线。但此方法一方面需要进行额外的跑车试验，增加试验工作量；另一方面，Szurgott等[7]的研究表明，对于某些形式的桥梁，如跨径较大的混凝土梁桥，由于结构阻尼引起的变形滞后性，在相同车辆荷载作用下，高速跑车试验位移时程曲线中的准静态分量可能小于低速跑车试验获得的准静态位移曲线，导致以此方法测得的冲击系数偏小，甚至出现负值冲击系数，不符合实际情况。

除去上述两种规范推荐方法，研究者们也从不同角度对实测冲击系数的计算方法进行研究。王永平等[8]利用Taylor级数对动位移曲线中的静态趋势项进行逼近。李伟钊等[9]采用低通滤波法进行动、静分离，根据桥梁的动响应数据确定滤波器截止频率。于明策[10]同样采用低通滤波法进行动、静分离，但采用了逐步试算法确定截止频率。耿泽[11]采用经验模态分解法对静位移的提取进行了尝试。徐松等[12]则基于实测数据的统计分析对冲击系数的计算方法进行研究。

综合目前的研究成果，低通滤波法是改进实测冲击系数计算方法的一个可行途径，在文献[4]中也建议，在条件允许的情况下可考虑采用低通滤波的方法进行时程曲线中动、静位移分离。但规范中并未给出具体的滤波方法设计指标，而低通滤波法的滤波结果会由于滤波器类型和截止频率选择的影响，导致滤波结果的不确定性，目前的研究多集中于截止频率的确定方法，但尚未有被广泛接受的滤波器设计方法。

基于此，在已有研究的基础上，提出频域幅值谱比对滤波法，以完成实测曲线的动、静分离。此方法针对准静态位移分量受测试条件干扰程度低、冲击系数检测不需要信号实时处理等工程特点，通过综合比对多条动位移时程曲线的频域幅值谱结果，可根据多条曲线幅值谱之间的相似性特点，自适应的确定滤波截止频率，以期有效地解决常用于动、静分离的低通滤波法截止频率估计困难的问题，提高实测冲击系数的计算准确性。

1 动位移曲线的组成分量

桥梁荷载试验中，冲击系数一般根据跑车激振试验所获得的动位移时程曲线进行计算。实测的桥梁动位移曲线是一条由准静态分量、多个振动分量和噪声叠加而成的波动曲线，对动位移曲线频域成分与时域波形的定性讨论，有助于对动、静分离方法的研究。为得出解析形式的解，选择简支梁桥作为代表对象进行分析，简化分析模型如图1所示。

图1 移动力匀速通过简支梁桥模型Fig.1 Model of a force driving through the simple beam bridge

以移动集中力P简化模拟车桥之间作用力，作用力P，可定性表示为

P=Fg+∑FicosΩit

(1)

式(1)中:Fg表示车重等恒定不变的常量力；∑FicosΩit表示由桥面不平整等因素引起的车桥间时变作用力，根据Fourier变换的基本思想，时变的作用力可等效为不同频率谐振力分量之和。在线弹性范围内，车辆过桥时桥梁的动位移曲线可看作式(1)中各荷载分量引起的桥梁位移曲线分量的叠加。

1.1 常量力作用

通过振型分解法可求解以动力作用下简支梁桥的动力响应。对于简支梁桥的跨中动位移，考虑一阶振型的贡献即可对真实位移做出良好的近似，所以在常量力Fg的作用下，简支梁的跨中位移时程曲线方程可表示为

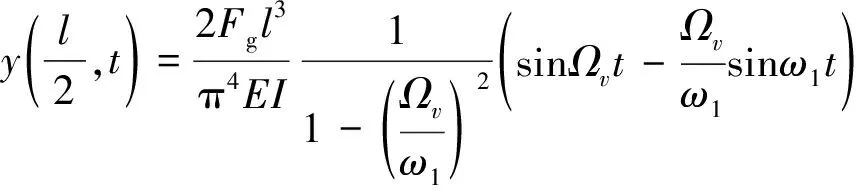
(2)

式(2)中:EI为截面抗弯刚度；L为桥梁长度；Ωv为移动荷载由速度引起的广义激振频率，Ωv=πv/l；ω1为桥梁一阶振动圆频率。所以，常量力作用下的位移曲线可近似看作两条正弦曲线的叠加：第一条低频曲线的波动频率为Ωv，在车辆过桥的时间段0 ～l/v内，曲线完成半个周期的振动，是一条正弦半波曲线；第二条高频曲线的波动频率为ω1，曲线振动周期数由车辆过桥时间决定，车速越慢，曲线上的波动越多。

另外，从静力的角度考虑，简支梁在相同大小集中力Fg作用下，跨中位置的位移影响线方程为

(3)

式(3)中:x为集中力作用位置。将式(3)与式(2)的前半部分正弦半波曲线方程(4)进行对比，

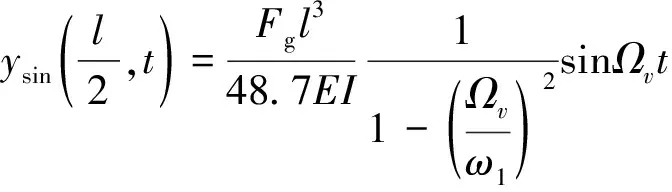
(4)

通过数值方法容易验证，二者无论是在最大幅值、还是曲线形状上，式(3)与式(4)都基本重合，而且二者之间误差的主要原因是由于式(4)仅选择了一阶振型参与计算，当考虑更多的模态组合时，误差将进一步减小。

所以，对于实测的桥梁动位移曲线，设法分离出其中包含的低频半波曲线，即可作为车辆过桥的准静态位移曲线。而且此曲线仅受恒定荷载大小和车辆过桥时间的影响，在现场多次重复性检测数据之间具有较好的稳定性。

1.2 简谐力作用

同样通过振型分解法，在单一频率简谐力分量FicosΩit的作用下，简支梁的跨中位移时程曲线方程如方程(5)所示，式(5)中各符号的含义与式(2)相同：

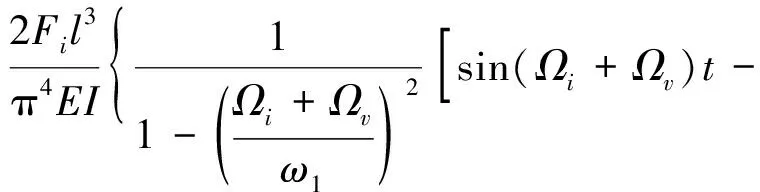
(5)

在移动简谐力作用下的简支梁跨中动位移曲线可看做三条正弦曲线的叠加，一条与常量力作用下的结果相似，是频率为ω1的高频曲线；另两条曲线的频率分别为Ωi+Ωv和Ωi-Ωv，一般情况下由于公路桥梁车速较低，Ωv要远小于Ωi，所以此两条曲线可近似认为频率相等，均为Ωi。在真实的车辆激励荷载中，包含的简谐力含有大量频率成分Ωi，所以最终桥梁动位移曲线中也含有丰富的频率分量。

综合常量力和简谐力的结果，可见在移动车辆荷载作用下的桥梁动位移曲线，表现为以准静态位移曲线为主要趋势项，其上叠加桥梁结构自振频率和外荷载激励频率所决定高频分量的振荡曲线。准静态位移成分控制了动位移曲线的总体位移大小，外荷载频率与结构自振频率曲线的叠加结果决定了在静位移基准上高频波动幅值的大小。在频域上，准静态趋势项决定了低频部分，波动曲线决定了高频部分。总体来说，动位移曲线的动、静分量分离，可以看作是曲线总体趋势的提取，也可以是曲线高、低频成分的分离。

2 频域幅值谱比对低通滤波法

由以上分析可见，在桥梁的动位移曲线中，准静态位移曲线包含了大部分的低频成分，而且由于频率较低，一般的车辆振动、路面颠簸和仪器噪声都不会明显的干扰到此频段，测试结果的稳定性较高，所以若能从测试数据中分离出此低频成分，即可实现动、静位移的分离。

在前文桥梁动位移曲线组成分量的分析中可看出，动位移曲线中的准静态分量曲线形状只与车辆重量有关，其他的动力影响因素的改变不会对准静态分量产生实质性的影响。对于一座检测桥梁，只要加载车辆重量保持不变，经过多次跑车激振获得的各条动位移曲线，虽然可能由于随机因素的干扰表现为不同的波动形态，但其中所包含的准静态位移分量是不变的。另外，桥梁检测中对检测信号的处理不要求实时性，不要求在信号记录的同时完成滤波操作，所以可允许对检测中获得的多条动位移曲线进行比较分析，利用多条曲线之间的相似性关系来完成准静态位移的分离。

在此基础上，提出一种改进的频域幅值谱比对低通滤波法用于准静态位的移提取，具体方法如下：

随着水平井技术在埋藏深、厚度薄、分布散的稠油油藏大规模应用，较充分地动用了该类难动用储量。但是随着热采吞吐周期的增加，地层能量越来越差，周期产量越来越低，周期效益逐渐变差。水平井蒸汽驱技术能够解决开发后期的生产矛盾，现河采油厂在乐安油田草33稠油油藏开展水平井井网下的蒸汽驱技术研究，优化转驱时机、注采参数等油藏工程参数。

(1) 使用同一加载车辆进行两次跑车试验，获得两条数据长度均为N的桥梁动位移曲线信号S1n和S2n(n=1,2,…,N)。

(2) 对记录的动位移信号做FFT变换，得到两组动位移信号的频域幅值谱A1k和A2k(k=1,2,…,N)。将两条跑车曲线的频域幅值谱进行对位比较，计算二者相同频率处的幅值相对偏差倍率：

(6)

(3)设定一偏差阈值，在低频段由低向高对各频点的频率偏差倍率进行判定，偏差倍率小于阈值的频点即认为由准静态位移控制，予以保留。由于准静态位移主要由低频信息控制，所以当偏差开始超过阈值时，此频率即作为低通滤波的截止频率，后续高频频点不再进行判定，全部置零，相当于进行理想矩形窗函数低通滤波。

(4) 对经过低通置零处理的频谱进行FFT逆变换，得到准静态位移曲线。

3 数值算例

3.1 计算模型

通过有限分析软件ANSYS的瞬态动力分析模块模拟计算车辆通过桥梁时，桥梁的动力位移时程曲线。计算模型通过梁单元对桥梁进行建模，通过质量块单元和弹簧阻尼单元对车辆模型进行建模，计算过程中按数组进行分步荷载施加，可模拟桥面不平整的影响。计算模型如图2所示。

图2 车辆模型匀速驶过简支梁Fig.2 Simply supported beam with uniformvelocity vehicle model

3.2 相同车速跑车实验

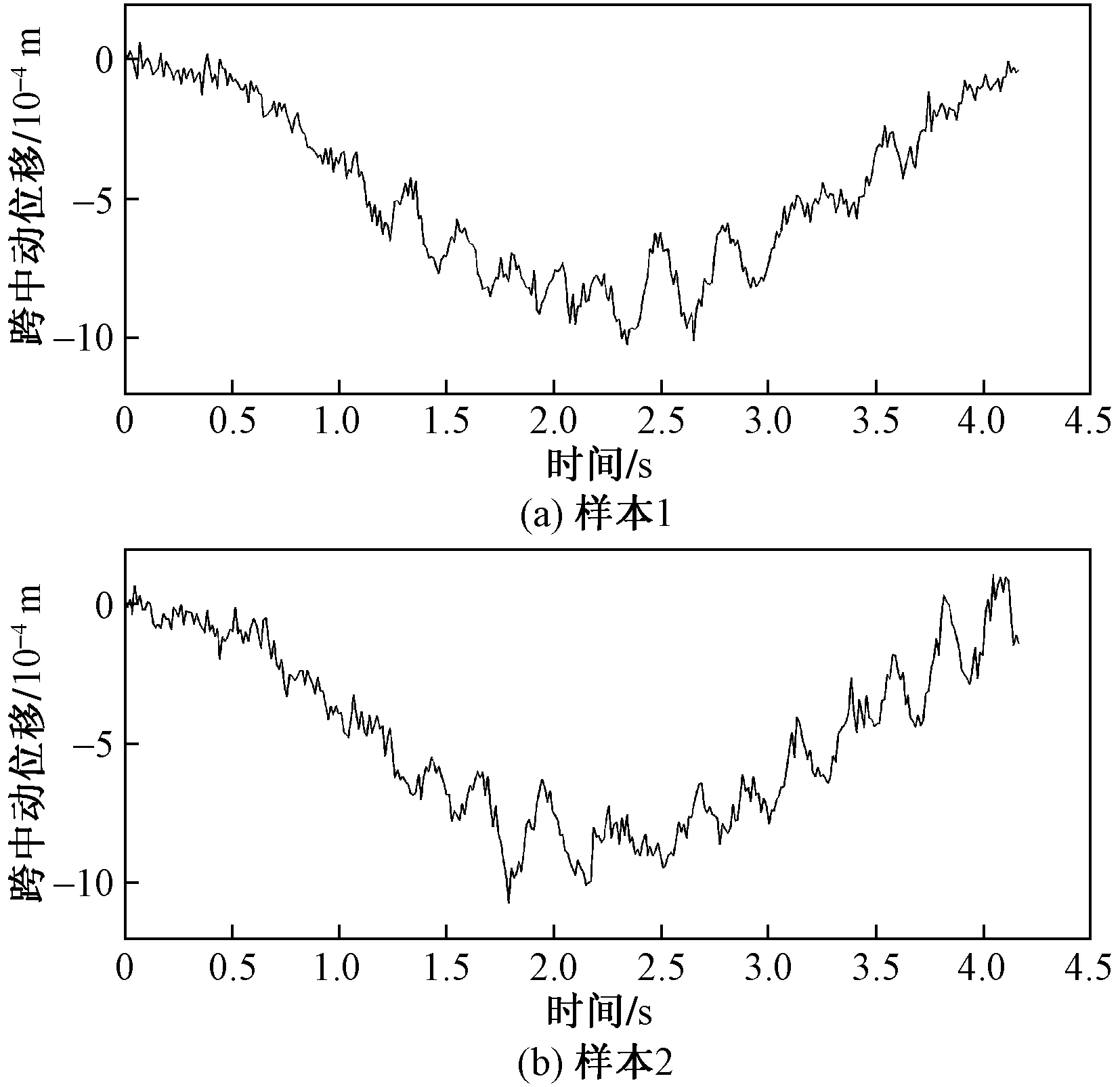
图3 简支梁跨中跑车实验动位移Fig.3 Dynamic displacement of moving truck test forsimply supported bridge

以L=30 m简支梁桥为例，模拟计算两次跑车实验测得的动位移曲线如图3所示，假定两次跑车实验车速相同，均为30 km/h，但两次跑车的行车轨迹并不完全相同，计算采用不同的桥面不平整曲线，并计入随机白噪声干扰。

对此两组动位移信号进行FFT变换，其频域幅值谱如图4所示。为保证两组数据的频谱能够准确对位，在进行FFT变换前，应注意将两组信号截取为相同的数据长度。由于信号中低频与高频部分的幅值相差过大，为方便显示，图4中的坐标y轴采用了对数坐标。

按式(6)计算两条动位移曲线幅值谱之间的相对偏差倍率Rk，结果如图5所示，由于只有低频段对准静态位移的提取有效，为使图形更加清晰，图5

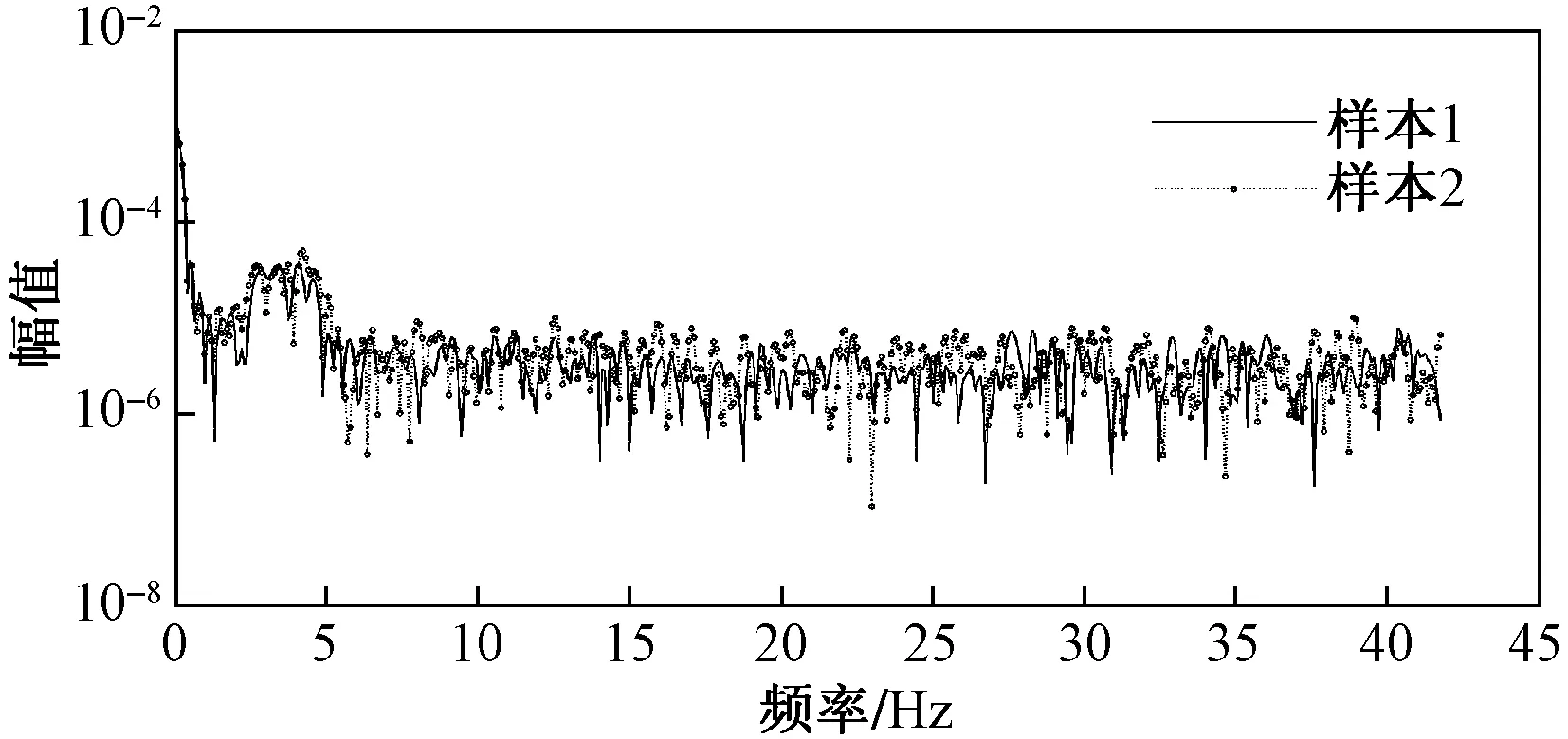
图4 简支梁桥动位移幅值谱Fig.4 Amplitude spectrums of the dynamic displacement data for simply supported bridge

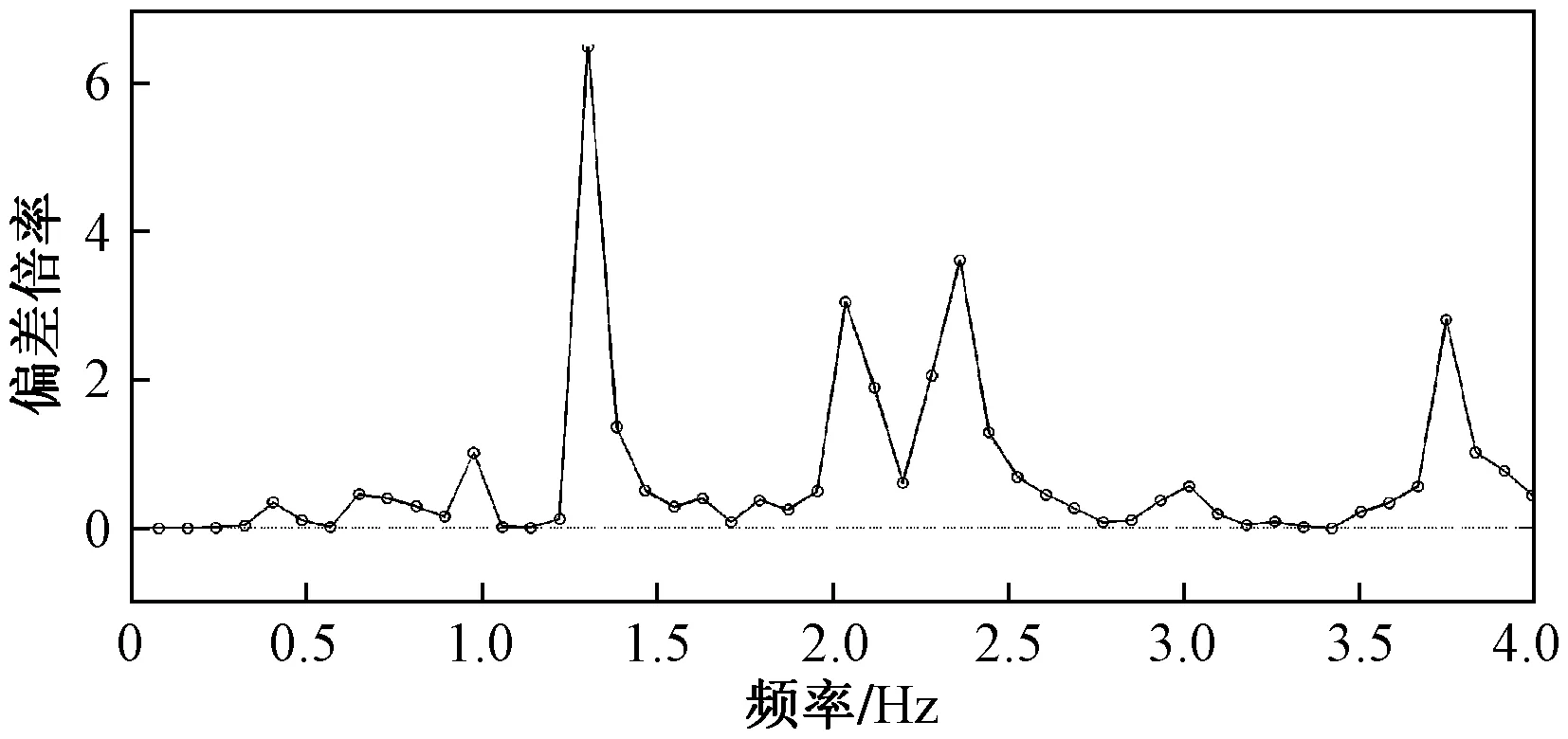
图5 简支梁桥动位移频谱幅值偏差Fig.5 Deviation degree of the amplitude spectrum forsimply supported bridge

中只给出低频部分的一段。

取频率偏差倍率阈值为0.4，根据图5中结果，动位移频谱中频率0.6 Hz以下频点的频率偏差小于阈值，可认为是准静态趋势项所控制的频点。将其余高频点全部置零，而后针对新得到的频谱进行FFT逆变换，得到低频滤波后的准静态位移逼近曲线，结果如图6所示。

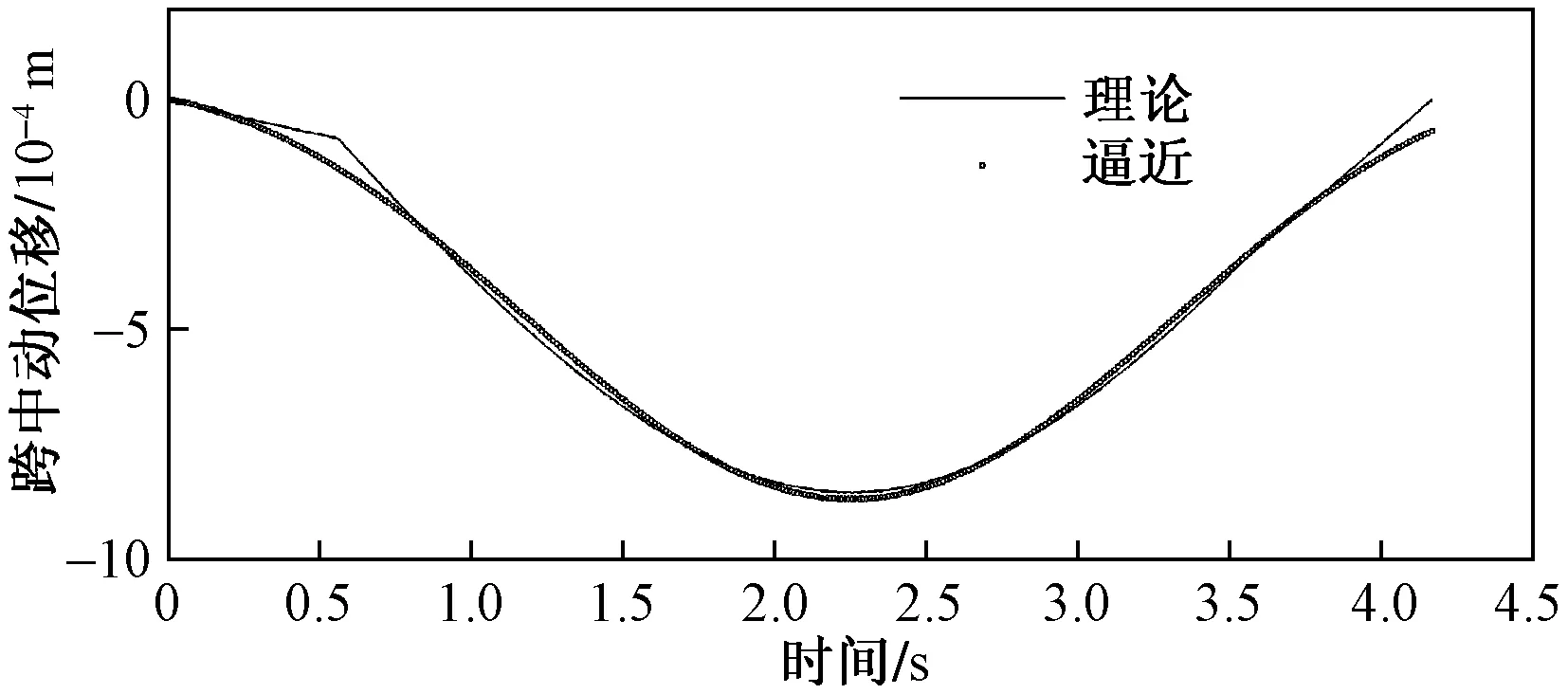
图6 简支梁桥准静态位移逼近曲线Fig.6 Approximating curve of the static displacement forsimply supported bridge

由于曲线局部位置的高频信息未能保留，所以滤波后的逼近曲线相对于理论真实曲线在转折点和端点的细节上存在细微偏差，但总体上拟合情况良好，峰值位置处偏差为0.64%，可满足工程精度要求。一般在桥梁检测的跑车试验中，同一工况均需进行多次跑车以保证测得有效的数据，所以此方法不增加实际试验的工作量，而且不需要预先对截止频率做出估计，避免了人为滤波器设计偏差对试验结果造成的影响。

3.3 不同车速跑车试验

在实际检测试验中，多次跑车的车速客观上难以完全相同，但在动、静分离的数据处理上，两次跑车试验车速不同，不仅不会影响准静态位移的识别，反而会使动、静分离频点更容易识别。因为，差别越大的动力激励荷载所引起的桥梁振动中的高频部分差异越大，但其中准静态趋势项却几乎不受影响，所以人为主观地选用不同车速作用下的动位移曲线，更有利于准静态位移曲线的提取。

在不同车速作用下，虽然准静态位移曲线在空间坐标轴上的形态是相同的，但由于车速越快，车辆过桥时间越短，所以准静态位移曲线在时间坐标轴上会随着车速增大而被逐渐压缩，在频域上会表现为低频部分的频点平移。此时再计算两条动位移曲线的幅值谱偏差时，不能再按照频率值进行对位，而应保证两条动位移曲线的数据长度相等的情况下，根据频点的序号来确定频点的位置。

为包含更多的分析工况，本例在上文桥梁结构参数的基础上，以3×30 m连续梁桥为例，模拟计算两次跑车试验的中跨跨中位置动位移曲线如图7所示，其中第一次车速为10 km/h，第二次车速为50 km/h，两次跑车的行车轨迹并不完全相同，计算采用不同的桥面不平整曲线，并计入随机白噪声干扰。

对动位移信号进行FFT变换，按频点序号进行对位，计算两曲线之间频域幅值的偏差倍率，前50个低频点结果如图8所示。

图7 连续梁桥中跨跨中跑车试验动位移Fig.7 Dynamic displacement of moving truck test forcontinuous beam bridge

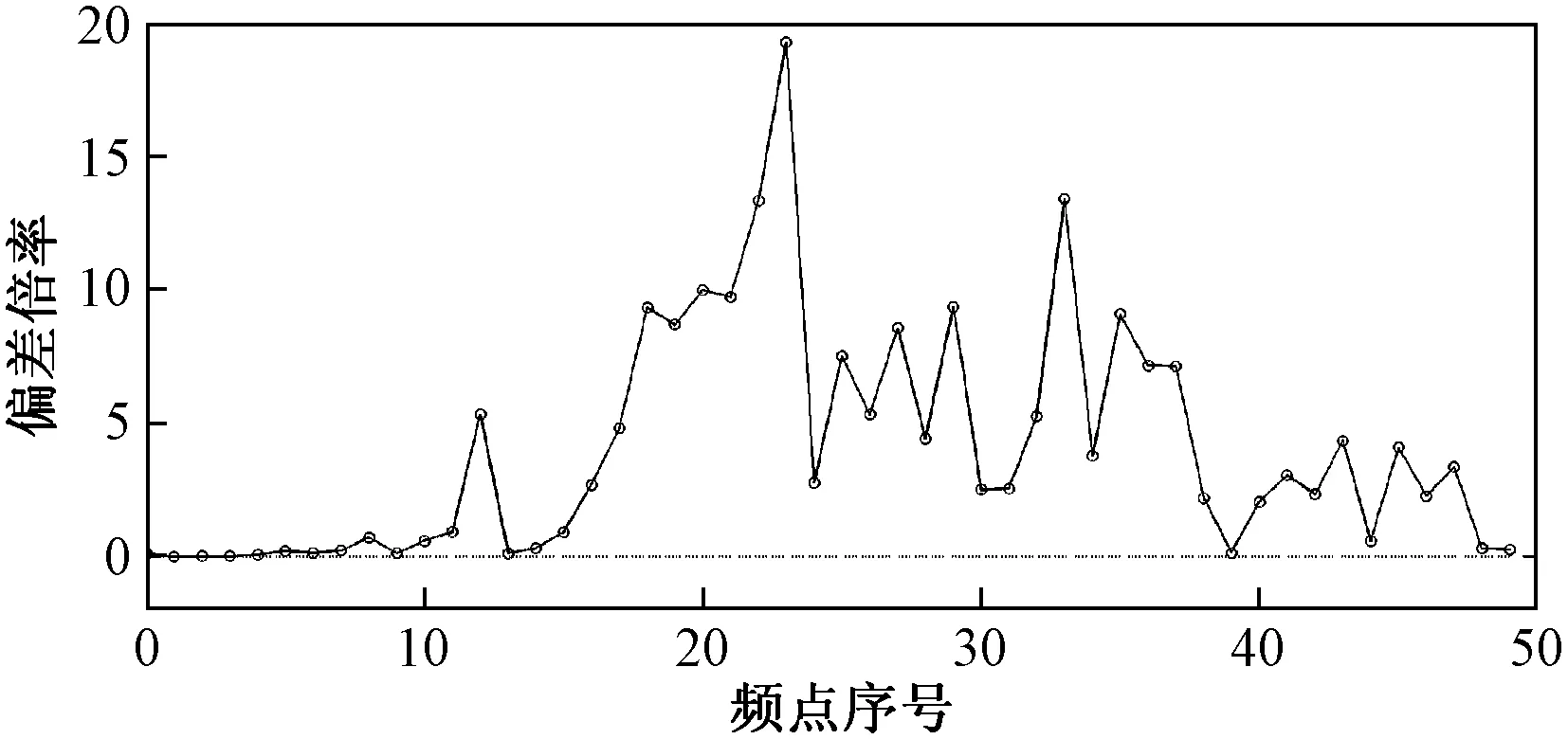
图8 连续梁桥动位移频谱幅值偏差倍率Fig.8 Deviation degree of the amplitude spectrum forcontinuous beam bridge

图9 连续梁桥准静态位移逼近曲线Fig.9 Approximating curve of the static displacement forcontinuous beam bridge

取频率偏差倍率阈值为0.4，在第九个频点处两条曲线的频率偏差超过阈值，所以选择前八个频点的作为准静态位移曲线的频域信息，对其进行FFT逆变换，得到逼近的准静态位移曲线如图9所示。可见逼近曲线与理论曲线拟合良好，在跨中峰值位置，二者偏差0.16%，可满足工程精度要求。

4 结论

根据研究可得出以下结论。

(1)移动车辆荷载作用下的桥梁动位移曲线，表现为以准静态位移曲线为主要趋势项，其上叠加桥梁结构自振频率和外荷载激励频率所决定高频分量的振荡曲线。在频域上，准静态趋势项决定了低频部分，波动曲线决定了高频部分。动位移曲线的动、静分量分离，本质上是信号总体趋势项的提取，或高、低频成分的分离。

(2)提出频域幅值谱比对低通滤波法，此方法针对准静态分量受测试条件干扰程度低、冲击系数检测不需要信号实时处理等工程特点，通过综合比对多条动位移时程曲线的频域幅值谱结果，可根据多条曲线幅值谱之间的相似性特点，自适应的确定滤波截止频率，有效地解决了常用于动、静分离的低通滤波法截止频率估计困难的问题。

(3)通过数值计算结果可验证，幅值谱比对滤波法对试验车速不敏感，动位移曲线测试车速不同时，不影响准静态位移的识别效果。同时，该方法受桥面不平整度、测试噪声等影响较小，具有良好的工程适应性。