基于分数阶微分的盐渍土电导率高光谱估算研究*
2020-04-08田安红赵俊三张顺吉付承彪熊黑钢
田安红, 赵俊三, 张顺吉, 付承彪**, 熊黑钢
基于分数阶微分的盐渍土电导率高光谱估算研究*
田安红1,2, 赵俊三2, 张顺吉1, 付承彪1**, 熊黑钢3,4
(1. 曲靖师范学院信息工程学院 曲靖 655011; 2. 昆明理工大学国土资源工程学院 昆明 650093; 3. 北京联合大学应用文理学院 北京 100083; 4. 新疆大学资源与环境科学学院 乌鲁木齐 830046)
传统电导率的反演模型采用整数阶微分(1阶或2阶)的预处理方法, 忽略位于分数阶微分处的高光谱反射率信息。因此, 本研究提出一种基于分数阶微分的盐渍土电导率高光谱估算方法, 以新疆昌吉回族自治州境内的盐渍化土壤为研究靶区, 于2017年5月采集0~20 cm的表层土壤样品, 利用FieldSpec®3 Hi-Res光谱仪测量盐渍土的野外高光谱, 并在实验室化验土壤的电导率理化参数。在Matlab 2019a软件中编程实现0阶-2.0阶的Grünwald-Letnikov分数阶微分计算(阶数间隔为0.1)。分析土壤高光谱与电导率的相关系数曲线在21种微分处的变化规律, 选择每阶微分的最大相关系数大于0.5时对应的波长为敏感波长, 采用逐步多元线性回归模型对电导率进行预测。结果表明: 分数阶微分预处理方法能够把相关系数曲线位于不同分数阶时的变化细节呈现出来, 在全波段范围内出现更多的波峰和波谷信息。电导率的8个敏感波长为400 nm、418 nm、567 nm、1 667 nm、2 132 nm、2 193 nm、2 257 nm和2 258 nm。估算电导率的最佳模型位于分数阶1.5阶, 其验证集的RPD值为1.99,2为0.81, RMSE为1.08, 该模型因RPD值大于1.8对电导率的估算能力好。本研究探索了电导率在不同分数阶微分处的差异信息, 为电导率的估算提供一种新的研究思路, 对新疆干旱区盐渍土的改良提供了科学可靠的依据。
盐渍土; 电导率; Grünwald-Letnikov分数阶微分; 敏感波长; 野外高光谱
电导率是衡量土壤盐渍化程度的重要评价指标[1],而土壤盐渍化是土地退化的主要表现之一, 在全世界范围内都是难以抑制的生态环境问题。新疆维吾尔自治区是中国重要的耕地后备资源[2], 但土壤的原生盐渍化现象, 以及人类不合理的开荒、放牧、耕种、建筑等干扰导致次生盐渍化现象非常严重。目前, 新疆维吾尔自治区盐渍土的总面积约为160万hm2[3]。土壤盐渍化会引起土壤生产力下降、酸碱失衡、土壤板结等后果[1], 严重制约了土地的可持续利用与生态系统的稳定性。因此, 对盐渍土信息的及时、精准、定量获取亦是当前研究的重点。传统土壤盐渍化检测是通过野外定点采样调查和实验室化学分析得到, 这种方法虽然精度高, 但费时、费力、成本高、效率低, 且稀疏采样导致检测的区域范围有限, 无法满足土壤在大范围连续地理空间的动态监测需求。高光谱技术具有快速、高效、动态、无污染、无破坏、光谱分辨率高、覆盖范围广、波段多且连续性强等优点, 为土壤盐渍化的大面积快速检测与评价提供了可能。
高光谱数据的预处理是高精度预测模型建立的关键。传统的电导率反演建模的预处理主要采用1阶或2阶微分的整数阶微分[4-5], 但其描述的系统物理模型仅仅是一种近似的处理方式, 没有考虑高光谱位于分数阶微分处的高光谱反射率细节信息[6]。然而, 分数阶微分是整数阶微分将阶次推广到任意阶的微分, 因其具有“记忆性”和“全局性”的优点, 能更清晰地刻画出系统的物理特性[7], 从而真实地揭示出研究对象的本质。直到最近几年, 才有学者将分数阶微分引入到土壤高光谱领域。例如, 张东等[8]采用分数阶微分研究新疆盐渍土的盐分与室内高光谱间的相关性, 与整数阶微分相比, 仿真表明分数阶微分提升相关性的结果更优, 且6种常见光谱变换均在分数阶0.6阶时达到通过0.01检验的最多波段数量。Hong等[9]采集汉江平原的土壤样本, 定量估算土壤有机质含量, 仿真表明位于分数阶1.25阶的偏最小二乘支持向量机模型反演效果最佳。Wang等[10]以新疆艾比湖湿地国家级自然保护区盐渍土为研究对象, 采用分数阶微分和灰色关联分析-BP神经网络模型对盐渍土的有机质含量进行定量估算, 仿真表明分数阶1.2阶的模型反演精度最高。Wang等[11]以新疆艾比湖的土壤样本为研究靶区, 对原始高光谱反射率进行吸光度变换和分数阶微分预处理, 结果表明基于1.5阶吸光度变换的随机森林模型对盐分的预测性能最优。
但上述研究中的土壤高光谱均在暗室理想的环境中测量, 且已有的分数阶微分研究主要针对土壤的盐分和有机质进行处理。然而, 分数阶微分对土壤电导率的估算研究少有报道, 且分数阶微分处理土壤野外高光谱更是鲜有报道。野外高光谱不仅能真实反映土壤样本的实际生长环境, 而且与卫星影像数据吻合度更高, 其研究价值更大。因此, 本研究选择新疆昌吉回族自治州境内的盐渍化土壤为研究靶区, 探索分数阶微分对野外高光谱的预处理结果, 并提取更多位于分数阶的波峰和波谷波段信息, 从而建立不同分数阶微分时对应的土壤电导率估算模型, 为电导率的预测提供一种新的研究思路, 对干旱区防治土壤盐渍化和促进精准农业的发展具有重要的参考价值。
1 材料与方法
1.1 研究区域概况
研究区为新疆昌吉回族自治州境内的盐渍化土壤区, 地理坐标为43°29′~45°45′N、87°44′~88°46′E。研究区域的日照非常充足, 夏季炎热, 冬季寒冷漫长, 降水非常稀少。年均气温达6.7 ℃, 全年无霜期为175 d。植被主要包含红柳()、猪毛菜()和梭梭(), 以及人工种植的榆树()、梭梭等育苗林地。
1.2 采样点布设与土壤样品采集
根据野外考察情况, 研究区与新疆102建设兵团的距离很近, 该区域经常受到人类日常活动的影响, 且近2年内有大部分土地被人工种植开发为育苗林地和榆树林地。在研究区布设采样线6条, 每条采样线上间隔400 m左右选择5个代表性的采样点, 共计30个采样点, 每个采样点面积2 m´2 m(图1)。土壤样品采集时间为2017年5月9—23日, 采集0~20 cm的表层土壤, 在每个采样点利用梅花五点混合法取样后混合均匀, 编号入袋, 样本带回实验室, 经过风干、研磨、移除杂物和过筛等操作后[12], 送到中国科学院新疆生态与地理研究所, 由研究所的专业实验人员测量土壤的电导率。

图1 研究区土壤采样点示意图
1.3 野外高光谱的测量与预处理
土壤野外高光谱利用FieldSpec®3 Hi-Res光谱仪测量, 波段为350~2 500 nm[13]。测量时间为当地时间13:00—15:00, 且选择晴朗无云和无风时刻测量, 尽量减少不利天气因素的影响。每个采样点按照梅花采样方法, 选择样点周围1 m范围的5个代表性的位置连续测量10次, 取50条高光谱反射率曲线平均值即为该采样点的高光谱反射率值。
因FieldSpec®3 Hi-Res光谱仪自身的误差和实地测试环境噪声的影响, 需要对野外高光谱进行预处理去噪。首先, 利用Savitzky-Golay平滑滤波方法对原始高光谱进行平滑。然后, 删除位于低信噪比的波段, 即350~399 nm和2 401~2 500 nm。最后, 删除位于水分吸收带1 400 nm和1 800 nm附近的波段, 即1 355~1 410 nm和1 820~1 942 nm。
1.4 高光谱分数阶微分方法
分数阶微分在信号分析、非线性动力学、生物医学等领域被广泛采用[14-19]。Grünwald-Letnikov (G-L)分数阶微分是最常用的一种形式。对于任何实数假设函数()在区间[,]上存在阶连续的导数, 则()的阶导数可以定义如下:
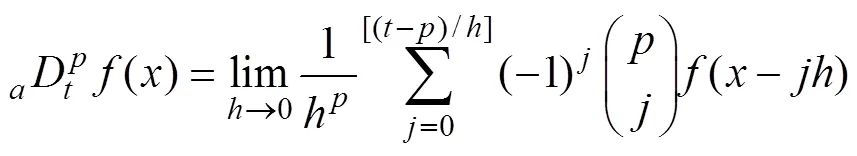
式中:是步长, [(-)/]表示(-)/的整数部分,表示微分的下限,表示微分的上限。当是正实数时, 公式(1)代表阶导数; 当是负实数, 则公式(1)代表阶积分。
函数()的1阶微分定义为:
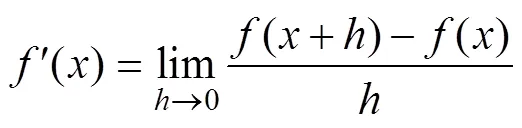
函数()的2阶微分定义为:
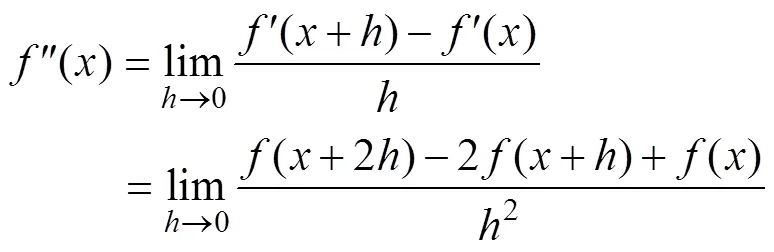
如果函数()的导数被提高到阶, 那么函数()的阶导数表示为:
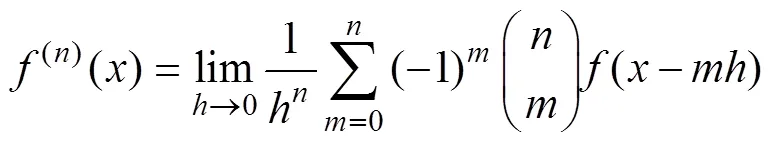
如果使用Gamma函数来代替公式(4)的二项式系数, 并将导数扩展为非整数阶, 可以得到Grünwald- Letnikov分数阶微分公式(1)。由于ASD光谱仪的重采样间隔为1 nm, 因此在公式(1)中, 令=1, 则函数()的阶分数阶微分的表达式可推导如下:

由公式(5)可知, 某波段在阶分数阶微分的值不仅与当前该波段的高光谱反射率()有关, 还与该波段以前的所有波段的高光谱反射率有关, 即与(-1)、(-2)、(-3)、…、(-)有关。并且在数值的计算过程中, 距离当前时刻越近的点, 被赋予的权重值也越大, 对阶分数阶微分值的影响也越大; 而距离当前时刻越远的点, 被赋予的权重值也越小, 对阶分数阶微分值的影响也越小。该性质体现出分数阶微分的“记忆性”和“全局性”特点, 也正是分数阶微分与整数阶微分的区别之处。
1.5 建模与检验方法
本研究采用逐步多元线性回归方法(stepwise multiple linear regression, SMLR)建模, 模型的精度利用决定系数(2)、均方根误差(RMSE)和相对分析误差(RPD)评估[20-22]。一个好的预测模型需要具有较大的RPD和2, 以及较小的RMSE。预测模型的2越接近于1, 说明模型的稳定性越好, 拟合度越高。预测模型的RMSE越小, 说明模型的预测精度越高。模型是否具有预测能力取决于RPD值的大小, 当RPD值为2.0~2.5时, 说明模型预测能力非常好[23-24];当RPD值为1.8~2.0时, 说明模型预测能力好; 当RPD值为1.4~1.8时, 说明模型预测能力一般; 当RPD值<1.4时, 说明模型预测能力差; 当RPD值<1.0时, 说明模型预测能力非常差, 不能进行预测。
2 结果与分析
2.1 电导率的统计分析
按照Kennard-Stone (K-S)算法, 对30个土壤样本进行划分, 其中建模集样本18个, 验证集样本12个。由研究区土壤电导率的统计特征(表1)可知, 建模集的电导率平均值为4.328 mS×cm-1, 变异系数为62.361%, 属于中等程度变异。验证集的电导率平均值为4.667 mS×cm-1, 变异系数为52.175%, 同样属于中等程度变异。全部样本的电导率平均值为4.463 mS×cm-1, 变异系数为57.338%, 属于中等程度变异。因此, 全部样本的平均值与变异系数都是在建模集和验证集的平均值与变异之间。说明建模集和验证集的样本划分合理。

表1 样本集土壤电导率的统计特征
2.2 分数阶微分对土壤高光谱与电导率相关性的影响
在Matlab 2019a软件中编程实现Grünwald- Letnikov分数阶微分的计算, 且分数阶微分的阶数间隔选取为0.1, 起始阶数为0阶, 终止阶数为2.0阶, 共有21种分数阶微分处理方式。分析土壤高光谱与电导率的21种分数阶微分的相关系数, 并在0.01水平下检验相关系数的显著性(图2)。在0阶-0.7阶之间没有任何波长通过0.01检验, 从0.8阶起到2.0阶之间都有波长通过0.01检验, 且通过的波长数量0.8阶1个、0.9阶6个、1.0阶35个、1.1阶47个、1.2阶51个、1.3阶47个、1.4阶40个、1.5阶37个、1.6阶32个、1.7阶28个、1.8阶28个、1.9阶29个、2.0阶31个。在分数阶1.1阶、1.2阶、1.3阶、1.4阶和1.5阶, 通过0.01检验的波长数量都大于整数阶1.0阶和2.0阶。
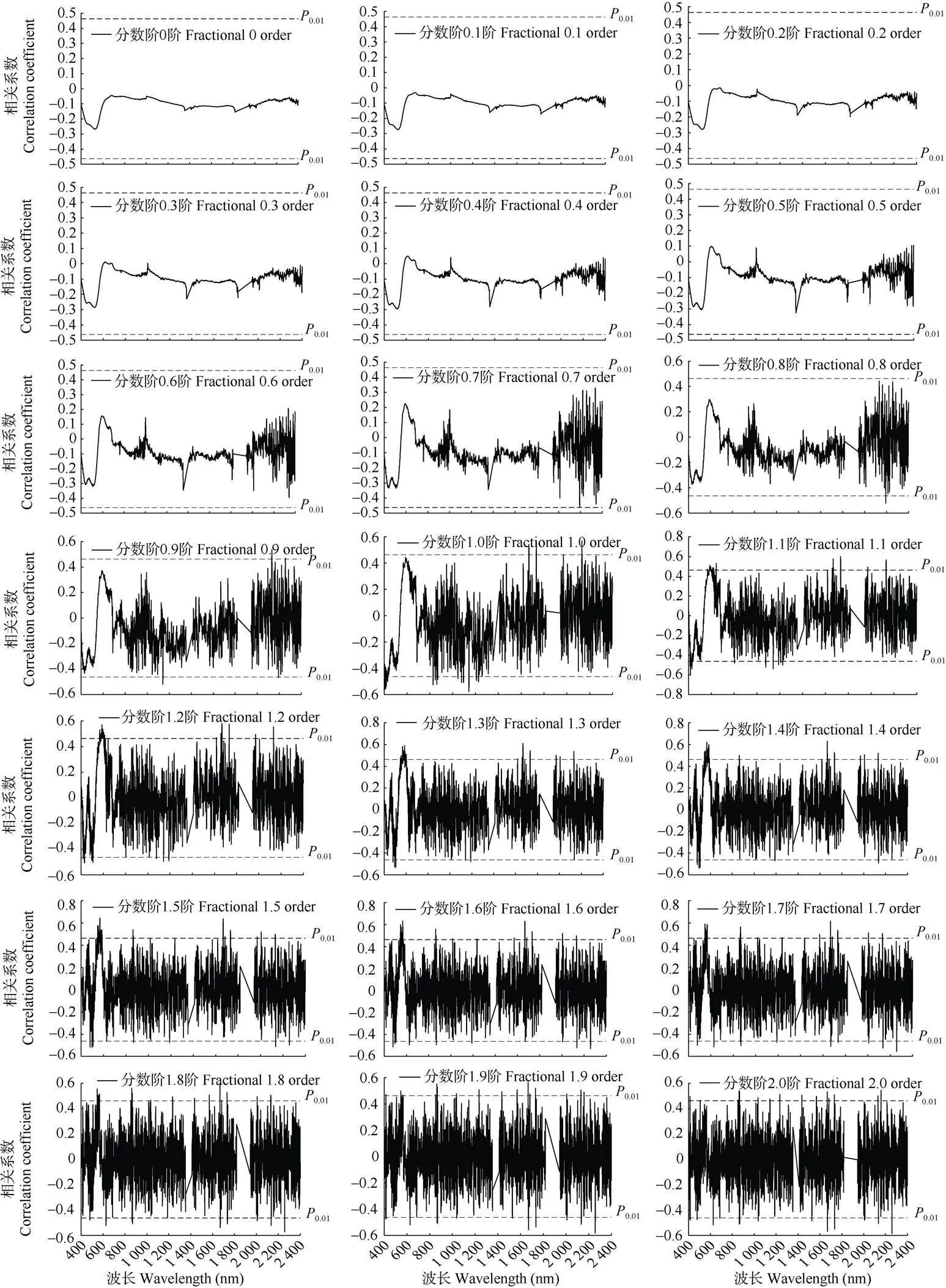
图2 土壤高光谱与电导率在0阶-2.0阶之间的相关系数
<|0.01|表示极显著相关。<|0.01|shows extremely significant correlation.
图2还显示, 当分数阶微分的阶数从0阶递增到1.0阶时, 相关系数曲线表现出一种渐变的变化过程, 尤其是在400~700 nm和1 000~1 400 nm波长范围内的渐变趋势更为明显, 且通过0.01检验的波长数量逐渐增加。当分数阶微分的阶数从1.1阶递增到2.0阶时, 各阶微分的相关系数曲线的波动性比较大, 渐变过程变现不太明显, 且通过0.01检验的波长数量逐渐减少。这说明分数阶微分预处理方法能够把相关系数曲线位于不同分数阶时的变化细节呈现出来, 在全波段范围内出现更多的波峰和波谷信息, 为后续敏感波段的选择提供了更多有用信息。
2.3 敏感波长选择
进一步统计不同分数阶微分时土壤高光谱和电导率的最大相关系数值及对应的波长(图3), 最大相关系数出现在分数阶1.5阶, 值为0.64, 对应波长为567 nm。整数阶1.0阶与2.0阶的最大相关系数均小于分数阶1.1阶、1.3阶、1.4阶、1.5阶、1.6阶与1.7阶的最大相关系数。因两个变量的相关系数绝对值在0.5与0.8之间, 说明两个变量是中度相关[25]。本研究选择每阶分数阶微分的最大相关系数大于0.5时对应的波长为敏感波长。图3显示在分数阶0.8阶-2.0阶对应的最大相关系数都大于0.5阶, 且0.8阶、0.9阶、1.0阶、1.1阶、1.2阶、1.3阶、1.4阶、1.5阶、1.6阶、1.7阶、1.8阶、1.9阶和2.0阶的最大相关系数对应的波长分别为2 193 nm、2 132 nm、400 nm、418 nm、1 667 nm、1 667 nm、1 667 nm、567 nm、567 nm、1 667 nm、1 667 nm、2 258 nm、2 257 nm。因此, 本研究选择的8个敏感波长为400 nm、418 nm、567 nm、1 667 nm、2 132 nm、2 193 nm、2 257 nm和2 258 nm。
2.4 不同分数阶微分阶数对应的电导率估算模型
采用8个敏感波长对应的高光谱反射率值为自变量(波长), 建模集的18个土壤样本的电导率值为因变量(), 建立多元线性回归模型, 预测验证集的12个土壤样本的电导率值(表2)。按照模型精度的评价参数指标, 对21个模型的估算结果分析发现, RPD值大于1.8的模型只有1个, 且位于分数阶1.5阶, 验证集的RPD值为1.99,2为0.81, RMSE为1.08, 验证集的2和RMSE分别为0.69和2.06, 说明建模集和验证集的稳定性和拟合度都较好, 预测误差较小, RPD值在1.8与2.0之间, 说明该模型对电导率的估算能力好, 回归模型为:
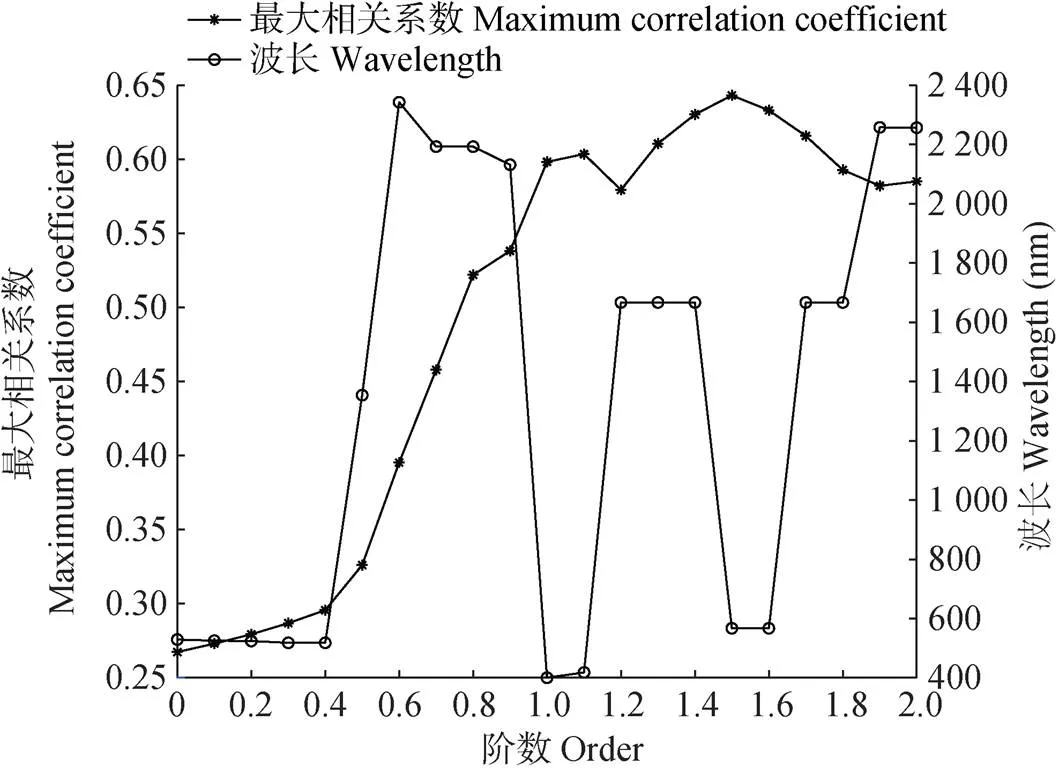
图3 不同分数阶微分阶数对应的土壤高光谱和电导率最大相关系数和波长
=4.4+274.4400–1 893418+712.6567–1 196.51667+
677.52132–674.22193+1 3792257–947.62258(6)
RPD值介于1.4~1.8的模型有5个, 且均是位于分数阶1.1阶、1.2阶、1.3阶、1.4阶和1.5阶, 这5个模型对电导率的估算能力一般。位于其他分数阶的模型因RPD值均小于1.4, 对电导率的估算能力差。因此, 位于分数阶1.5阶的多元线性回归模型对研究区的电导率预测能力好, 且是电导率估算的最优模型。
从不同分数阶微分阶数对应的实测值与预测值的散点图(图4)看出, 与传统整数阶微分1.0阶和2.0阶相比较, 分数阶1.5阶建立的模型的数据点较为均匀地分布在拟合线的两侧, 且最为接近1∶1直线, 电导率的预测值与实测值的拟合方程可表示为=0.788 26+0.658 88,2为0.81。
3 讨论与结论
土壤盐渍化程度可以通过盐分含量和电导率来反映, 但已有研究表明土壤高光谱数据对电导率的响应比盐分的响应更为敏感[26], 因此采用电导率替代盐分监测土壤盐渍化程度的高光谱反演研究是一种高效快捷的方法。以往对土壤电导率的高光谱反演建模主要采用整数阶微分(1.0阶或2.0阶)的预处理方式。杨爱霞等[5]以新疆艾比湖的盐渍土为研究对象, 利用磁感应电导仪测量土壤的电导率, 并对高光谱数据进行整数阶1.0阶和2.0阶微分预处理, 仿真结果表明整数阶1.0阶微分处理后的支持向量机反演模型是最优估算模型。李相等[27]以新疆渭干河-库车河的盐渍土为研究对象, 对高光谱数据进行原始1.0阶微分变换、原始对数倒数1.0阶微分变换和连续统去除1.0阶微分变换的预处理方式, 利用一元线性回归模型和逐步多元回归模型预测土壤电导率和盐分, 仿真表明以电导率构建的反演估算模型对应的决定系数大于含盐量构建的反演模型的决定系数。然而, 已有研究均忽略了模型位于分数阶的情况, 没有对比分析整数阶和分数阶的预测结果。因分数阶微分自身具有“记忆性”和“全局性”特点, 其对高光谱的处理注重的是高光谱曲线的全局性, 而整数阶微分对高光谱的处理注重的是高光谱曲线的局部性。因此本论文利用Grünwald-Letnikov分数阶微分公式对土壤原始高光谱进行微分计算, 深入挖掘出高光谱位于分数阶处的潜在信息, 建立比整数阶微分更多的模型, 从而增加更多的选择范围。
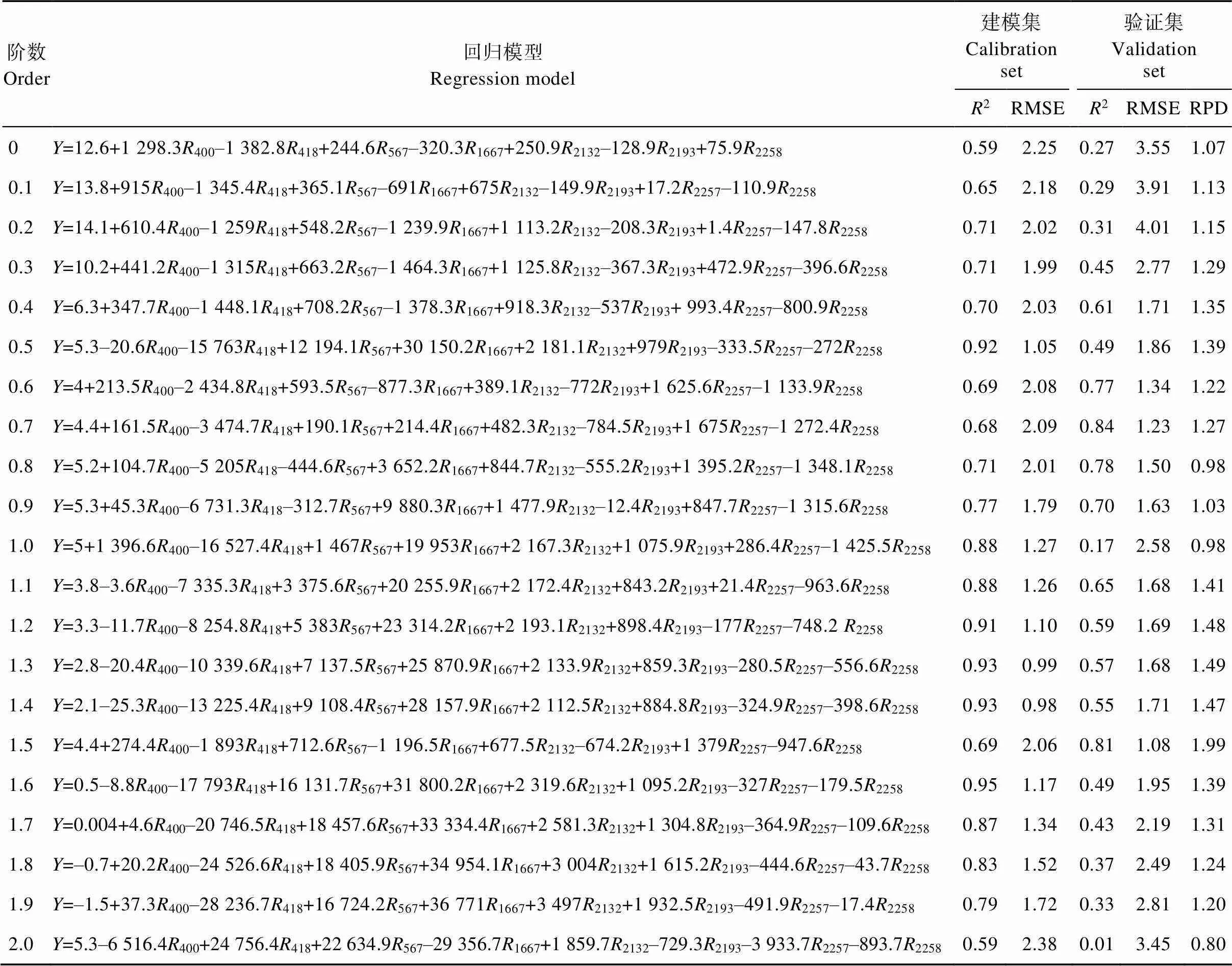
表2 8个敏感波长对应的土壤高光谱在不同分数阶微分阶次的电导率预测模型和预测精度
为高光谱反射率值, 下标数据为波长。is hyperspectral reflectance, subscript data is the wavelength.
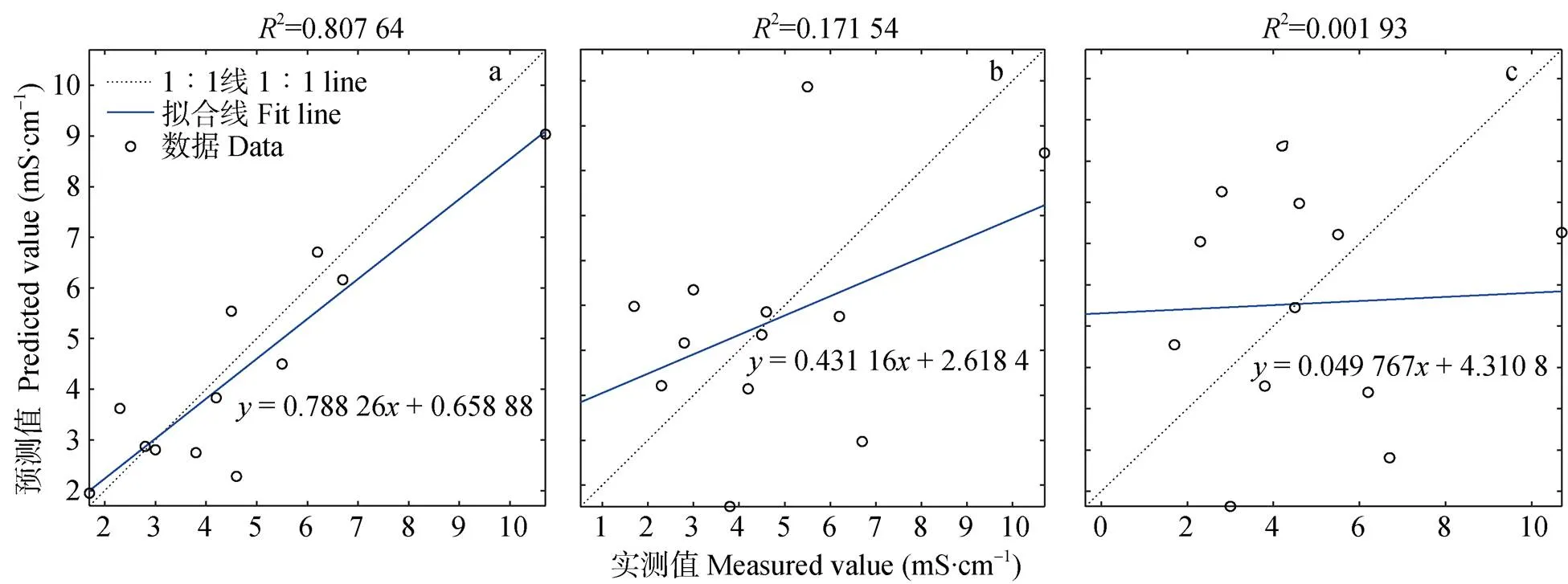
图4 1.5阶(a)、1.0阶(b)和2.0阶(c)微分对应的土壤电导率实测值与预测值的散点图
分数阶微分方法可以充分挖掘出土壤高光谱数据的有用信息, 其被广泛应用于研究土壤的盐分、有机质、速效钾等[28-30], 但分数阶微分对土壤电导率的报道研究则很少。本文对土壤高光谱数据进行分数阶微分预处理, 计算土壤高光谱和电导率在不同分数阶时的相关性, 挖掘出更多位于分数阶处的敏感波长, 采用SMLR模型建立21个模型, 对比分析在不同分数阶时的模型反演结果。研究发现位于分数阶的模型对电导率的估算精度大于位于整数阶的模型, 且位于分数阶1.5阶的SMLR模型是定量反演电导率的最佳模型, 其验证集RPD、2和RMSE分别为1.99、0.81和1.08, 建模集2和RMSE分别为0.69、2.06, 该模型的稳定性较好, 预测误差较小。而整数阶1.0阶和2.0阶的SMLR模型的RPD值均小于1.0, 说明本研究中的整数阶1.0阶和2.0阶模型对电导率的预测能力非常差, 不能对电导率进行预测。
本研究通过探索分数阶微分对野外高光谱的预处理结果, 建立不同分数阶微分时对应的土壤电导率估算模型, 为精确定量反演电导率提供了一种新的研究方法, 为新疆盐渍土的治理提供科学依据, 以促进干旱区土地资源的可持续发展。
[1] SCUDIEROE, SKAGGS T H, CORWIN D L. Comparative regional-scale soil salinity assessment with near-ground apparent electrical conductivity and remote sensing canopy reflectance[J]. Ecological Indicators, 2016, 70: 276–284
[2] PENG J, BISWAS A, JIANG Q S, et al. Estimating soil salinity from remote sensing and terrain data in southern Xinjiang Province, China[J]. Geoderma, 2019, 337: 1309–1319
[3] 孙永猛, 丁建丽, 瞿娟, 等. 应用电磁感应和遥感的新疆绿洲区域尺度盐渍土识别[J]. 农业工程学报, 2012, 28(20): 180–187 SUN Y M, DING J L, QU J, et al. Saline soil identification based on electromagnetic induction and remote sensing in Xinjiang Oasis[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(20): 180–187
[4] 彭杰, 王家强, 向红英, 等. 土壤含盐量与电导率的高光谱反演精度对比研究[J]. 光谱学与光谱分析, 2014, 34(2): 510–514 PENG J, WANG J Q, XIANG H Y, et al. Comparative study on hyperspectral inversion accuracy of soil salt content and electrical conductivity[J]. Spectroscopy and Spectral Analysis, 2014, 34(2): 510–514
[5] 杨爱霞, 丁建丽, 李艳红, 等. 基于表观电导率与实测光谱的干旱区湿地土壤盐分监测[J]. 中国沙漠, 2016, 36(5): 1365–1373 YANG A X, DING J L, LI Y H, et al. Apparent electronic conductivity and measured spectral for monitoring soil salt content in arid lakeside wetland[J]. Journal of Desert Research, 2016, 36(5): 1365–1373
[6] 张亚坤, 罗斌, 潘大宇, 等. 基于分数阶微分算法的大豆冠层氮素含量估测研究[J]. 光谱学与光谱分析, 2018, 38(10): 3221–3230 ZHANG Y K, LUO B, PAN D Y, et al. Estimation of canopy nitrogen content of soybean crops based on fractional differential algorithm[J]. Spectroscopy and Spectral Analysis, 2018, 38(10): 3221–3230
[7] LEYDEN K, GOODWINE B. Fractional-order system identification for health monitoring[J]. Nonlinear Dynamics, 2018, 92(3): 1317–1334
[8] 张东, 塔西甫拉提·特依拜, 张飞, 等. 分数阶微分在盐渍土高光谱数据预处理中的应用[J]. 农业工程学报, 2014, 30(24): 151–160 ZHANG D, TASHPOLAT·TIYIP, ZHANG F, et al. Application of fractional differential in preprocessing hyperspectral data of saline soil[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(24): 151–160
[9] HONG Y S, LIU Y L, CHEN Y Y, et al. Application of fractional-order derivative in the quantitative estimation of soil organic matter content through visible and near-infrared spectroscopy[J]. Geoderma, 2019, 337: 758–769
[10] WANG X P, ZHANG F, KUNG H, et al. New methods for improving the remote sensing estimation of soil organic matter content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in northwest China[J]. Remote Sensing of Environment,2018, 218: 104–118
[11] WANG J Z, DING J L, ABULIMITI A, et al. Quantitative estimation of soil salinity by means of different modeling methods and visible-near infrared (VIS-NIR) spectroscopy, Ebinur Lake Wetland, Northwest China[J]. Peer J, 2018, 6: e4703
[12] 王宁, 熊黑钢, 马利芳, 等. 新疆有无人为干扰下土壤盐分估算的比较[J]. 干旱区研究, 2019, 36(2): 323–330WANG N, XIONG H G, MA L F, et al. Estimation and comparison of soil salinity under different intensities of human disturbance in Xinjiang[J]. Arid Zone Research, 2019, 36(2): 323– 330
[13] 张子鹏, 丁建丽, 王敬哲. 基于谐波分析算法的干旱区绿洲土壤光谱特性研究[J]. 光学学报, 2019, 39(2): 0228003 ZHANG Z P, DING J L, WAMG J Z. Spectral characteristics of oasis soil in arid area based on harmonic analysis algorithm[J]. Acta Optica Sinica, 2019, 39(2): 0228003
[14] CARDONE A, D’AMBROSIO R, PATERNOSTER B. A spectral method for stochastic fractional differential equations[J]. Applied Numerical Mathematics, 2019, 139: 115– 119
[15] SHIRI B, BALEANU D. System of fractional differential algebraic equations with applications[J]. Chaos, Solitons & Fractals, 2019, 120: 203–212
[16] GARRAPPA R. Neglecting nonlocality leads to unreliable numerical methods for fractional differential equations[J]. Communications in Nonlinear Science and Numerical Simulation, 2019, 70: 302–306
[17] YUTTANAN B, RAZZAGHI M. Legendre wavelets approach for numerical solutions of distributed order fractional differential equations[J]. Applied Mathematical Modelling, 2019, 70: 350–364
[18] ARMAND A, ALLAHVIRANLOO T, ABBASBANDY S, et al. The fuzzy generalized Taylor’s expansion with application in fractional differential equations[J]. Iranian Journal of Fuzzy Systems, 2019, 16(2): 57–72
[19] MORET I, NOVATI P. Krylov subspace methods for functions of fractional differential operators[J]. Mathematics of Computation, 2019, 88(315): 293–312
[20] HONG Y S, CHEN S C, LIU Y L, et al. Combination of fractional order derivative and memory-based learning algorithm to improve the estimation accuracy of soil organic matter by visible and near-infrared spectroscopy[J]. Catena, 2019, 174: 104–116
[21] KUANG B, MOUAZEN A M. Effect of spiking strategy and ratio on calibration of on-line visible and near infrared soil sensor for measurement in European farms[J]. Soil and Tillage Research, 2013, 128: 125–136
[22] BALDOCK J A, HAWKE B, SANDERMAN J, et al. Predicting contents of carbon and its component fractions in Australian soils from diffuse reflectance mid-infrared spectra[J]. Soil Research, 2013, 51(8): 577–595
[23] SHI Z, WANG Q L, PENG J, et al. Development of a national VNIR soil-spectral library for soil classification and prediction of organic matter concentrations[J]. Science China: Earth Sciences, 2014, 57(7): 1671–1680
[24] 王海峰, 张智韬, KARNIELI A, 等. 基于灰度关联-岭回归的荒漠土壤有机质含量高光谱估算[J]. 农业工程学报, 2018, 34(14): 124-131 WANG H F, ZHANG Z T, KARNIELI A, et al. Hyperspectral estimation of desert soil organic matter content based on gray correlation-ridge regression model[J]. Transactions of the Chinese Society of Agricultural Engineering, 2018, 34(14): 124-131
[25] TIAN A H, ZHAO J S, XIONG H G, et al. Application of fractional differential calculation in pretreatment of saline soil hyperspectral reflectance data[J]. Journal of Sensors, 2018, 2018: 8017614
[26] 李娟, 陈超, 王昭. 基于不同变换形式的干旱区土壤盐分高光谱特征反演[J]. 水土保持研究, 2018, 25(1): 197–201 LI J, CHEN C, WANG Z. Inversion of high spectral characteristics of soil salt in arid area based on different transform forms[J]. Research of Soil and Water Conservation, 2018, 25(1): 197–201
[27] 李相, 丁建丽, 侯艳军, 等. 干旱半干旱区土壤含盐量和电导率高光谱估算[J]. 冰川冻土, 2015, 37(4): 1050–1058LI X, DING J L, HOU Y J, et al. Estimating the soil salt content and electrical conductivity in semi-arid and arid areas by using hyperspectral data[J]. Journal of Glaciology and Geocryology, 2015, 37(4): 1050–1058
[28] ZHANG D, TIYIP T, DING J L, et al. Quantitative estimating salt content of saline soil using laboratory hyperspectral data treated by fractional derivative[J]. Journal of Spectroscopy, 2016, 2016: 1081674
[29] FU C B, GAN S, YUAN X P, et al. Impact of fractional calculus on correlation coefficient between available potassium and spectrum data in ground hyperspectral and landsat 8 image[J]. Mathematics, 2019, 7(6): 488
[30] WANG J Z, TASHPOLAT T, DING J L, al. Desert soil clay content estimation using reflectance spectroscopy preprocessed by fractional derivative[J]. PLoS One, 2017, 12(9): e0184836
Hyperspectral estimation of saline soil electrical conductivity based on fractional derivative*
TIAN Anhong1,2, ZHAO Junsan2, ZHANG Shunji1, FU Chengbiao1**, XIONG Heigang3,4
(1.College of Information Engineering, Qujing Normal University, Qujing 655011, China; 2. Faculty of Land Resource Engineering, Kunming University of Science and Technology, Kunming 650093, China; 3. College of Applied Arts and Science, Beijing Union University, Beijing 100083, China; 4. College of Resource and Environment Sciences, Xinjiang University, Urumqi 830046, China)
The integer-order differential (first-order or second-order) preprocessing method is often used in traditional electrical conductivity inversion models, but it ignores the hyperspectral reflectance information at the fractional-order differential. In this paper, a hyperspectral method based on fractional differential to estimate the electrical conductivity of saline soil was proposed. The salinized soil in Changji, Xinjiang was used as the research subject. The surface soil samples of 0-20 cm were collected in May 2017, the field hyperspectral of the saline soil was measured by a FieldSpec®3 Hi-Res spectrometer, and physical and chemical parameters of soil electrical conductivity were tested in the laboratory. Next, the Grünwald-Letnikov fractional derivative calculation between 0.0-order and 2.0-order was programmed in MATLAB 2019a software (order interval is 0.1). Then, the variation law of the correlation coefficient curves between soil hyperspectral and electrical conductivity under 21 kinds of differentials was analyzed. When the maximum correlation coefficient of each fractional derivative was greater than 0.5, the corresponding wavelength was selected as the sensitive wavelength. Finally, the stepwise multiple linear regression model was used to predict the electrical conductivity. The results showed that the fractional derivative preprocessing method could display the variation details of the correlation coefficient curve under different fractional orders, and more peaks and troughs appeared in the whole band. The eight sensitive wavelengths of electrical conductivity were 400 nm, 418 nm, 567 nm, 1 667 nm, 2 132 nm, 2 193 nm, 2 257 nm, and 2 258 nm. The best model for estimating electrical conductivity was located at the 0.5th-order. The relative percent difference (RPD) value of the verification set was 1.99, the determination coefficient (2) was 0.81, and the root mean square error (RMSE) was 1.08. This model had the ability to estimate the electrical conductivity because the RPD value was greater than 1.8. This study explored the difference in electrical conductivity estimates under different fractional derivatives and provided a new method for electrical conductivity estimation, which could be of considerable value for research into improvement of saline soils in the arid regions of Xinjiang.
Saline soil; Electrical conductivity; Grünwald-Letnikov fractional derivative; Sensitive wavelength; Field hyperspectral

S151.9
10.13930/j.cnki.cjea.190865
田安红, 赵俊三, 张顺吉, 付承彪, 熊黑钢. 基于分数阶微分的盐渍土电导率高光谱估算研究[J]. 中国生态农业学报(中英文), 2020, 28(4):599–607
TIAN A H, ZHAO J S, ZHANG S J, FU C B, XIONG H G. Hyperspectral estimation of saline soil electrical conductivity based on fractional derivative[J]. Chinese Journal of Eco-Agriculture, 2020, 28(4): 599–607
* 国家自然科学基金项目(41901065, 41671198, 41761081)、教育部产学合作协同育人项目(201802156014)和曲靖师范学院教师教育研究专项项目(2019JZ001)资助
付承彪, 主要研究方向为高光谱遥感图像处理。E-mail: fucb305@163.com
田安红, 主要研究方向为盐渍土的高光谱反演。E-mail: tianfucb@163.com
2019-12-10
2020-02-04
* This study was supported by the National Natural Science Foundation of China (41901065, 41671198, 41761081), the Industry-University Cooperation Collaborative Education Project of Ministry of Education of China (201802156014), and the Teacher Education Research Project of Qujing Normal University of China (2019JZ001).
, E-mail: fucb305@163.com
Dec. 10, 2019;
Feb. 4, 2020
