噪声干扰下的防羽布疵点检测算法

张团善,石 玮

(西安工程大学 机电工程学院,陕西 西安 710048)

0 引 言

织物疵点主要是在织造过程中形成的[1]。随着需求的增加、生产效率不断提升[2],生产过程中织物的疵点数目和种类也会随之增多,而产品表面缺陷会降低产品质量和商业价值[3]。研究表明，纺织品的价格会因生产质量的问题而损失45%～65%[4]。目前,国内几乎所有纺织企业仍然釆用传统的人工验布方式进行瑕疵检测,通过人眼观察,手动剔除不合格产品。由于检测劳动强度大,人为检测效率低,漏检率较高,可靠性较差[5],并增加企业劳动成本[6]。采用机器视觉[7]检测技术,能够使检测实现自动化,并且高速高效地检测织物疵点,保证产品的质量。

因为织物在生产过程中环境的复杂性，生产材料和产品的多样性,使织物疵点检测算法缺乏通用性。织物疵点检测被许多从事此领域的研究人员认为是一个非常艰巨的任务[8]。目前，针对织物疵点检测算法可分为基于统计信息的方法[9]、基于模型的方法[10-11]、基于频谱的方法[12]、基于卷积神经网络的方法[13]和基于显著性的方法等。韩立伟等[14]通过实时收集图像的特征, 分析有价值的统计信息,将有价值的信息进行模板更新和阈值的判断。该方法适用于纹理结构清晰，纹理具有周期性的布匹,但对于密度较高、反光较强的防羽布检测效果不佳。闵信军等[15]利用图像分块处理灰度共生矩阵进行疵点检测。该方法利用分块提取图像灰度共生矩阵特征纹理,分析纹理特征值的分布状况,查找疵点并且确定疵点所在区域。不过，该方法在防羽布检测时易受光照噪声的影响。张波等[16]采用相对总变差模型对织物图像进行滤波，以去除织物纹理,然后在得到的灰度图像上直接进行基于自适应邻域的灰度形态学运算,最终得到织物疵点的增强图像。该方法在防羽布的检测中同样易受环境噪声的影响,并且模型信息不足，与实际纹理具有一定差异,因此检测精度不高。频谱方法主要有小波变换系数[17]、傅里叶变换[18]、Gabor滤波器[19]和轮廓线变换[20]等,其过程是将图像由空间域转换为频域,通过频谱的分布描述纹理中的全局周期性质。肖乐等[21]利用Gabor滤波器和建立图像金字塔对多幅图像进行融合与重建提取疵点,但在防羽布的疵点检测中,最优Gabor滤波器参数的选择难度很大。

本文研究对象是以超细涤纶为原料的740/620高密防羽布，具有透气性较好, 撕破强度高, 耐磨性能好,布面光洁匀整等特征。由于防羽布具有上述特性,在防羽布大规模生产的过程中会出现光照分布不均，布匹易褶皱等现象。目前织物疵点检测算法虽然具有一定的普遍性、通用性,但由于织物的纹理、材料和生产环境的多样性和差异性,因此对不同种织物的疵点检测效果并不理想。本文提出一种针对高密度织物检测算法。该方法利用灰度单通道图,提取图像上每个像素及其8个邻域像素的变化特征；利用疵点像素与非疵点像素变化差异确定疵点因子,通过对比得到织物疵点二值图。该算法虽在通用性、普遍性上尚有一定的局限性,但在光照不均匀、布面不平整等复杂环境下的防羽布疵点检测具有很好的检测性能。

1 算法设计

设图像为m×n的RGB三通道图像,由于疵点类型为非色差类疵点,在不影响对织物检测的前提下,为减少图像处理计算量,方便后续计算,将图像通过式(1)进行灰度变换。

Gray=0.299R+0.587G+0.114B

(1)

式中：R,G,B均为单通道矩阵。灰度图像矩阵Gray表示为

(2)

式中：ai,j∈[0,255],i∈[0,m],j∈[0,n]。

为实现对微小和不显著疵点的准确检测,选取大小为3×3,像素数目为9的基矩阵aω,表达式为

(3)

式中：ω=1,2,…,(m-1)×(n-1)；i=1,2,…,m-1;j=1,2,…,n-1。

由于光照分布不均、布匹不平整等噪声和疵点在灰度图像中都是通过像素值变化体现,因此通过像素变化的差异分析图像。由式(4)计算图像差异矩阵bω,得到差异矩阵式(5)。

(4)

(5)

在噪声环境的疵点图像中,疵点区域、噪声区域和非疵点区域具有不同的变化趋势,对应于差异矩阵中不同的差值。具体分为以下3种情况:

1) 正常织物区域无较大差值变化;

2) 光照分布不均、布匹褶皱等噪声区域差值变化趋势具有均匀性;

3) 疵点区域差值变化趋势具有突变性。

计算差异矩阵像素变化波动值Sω

将Sω与差异矩阵均值mω(见式(4))的对数进行比较,根据式(6)定义疵点因子ε。

(6)

式中：c为常数,c=1,2,…。

Sω的大小可以直观反应基矩阵内像素变化的波动性。通过动态判断差异矩阵bω中的像素bi,j与疵点因子ε的大小,得到对应区域中每个像素的像素值。若疵点因子大于像素变化差异值,则定义为非疵点像素点(像素值为0);否则,定义为疵点像素点(像素值为255)。进而得到整幅图像每个像素的像素值。为使图像更具有直观性和可控性,通过式(7)得到动态二值图像矩阵th。

(7)

式中:ci,j表示二值化后像素值,且

经过上述计算得到的二值图中含有由噪声引起的斑点。为解决这个问题,通过式(8)对最终生成的二值图进行中值滤波,得到图像矩阵I*。

(8)

式中：M为中值滤波算子。

综上分析,防羽布疵点检测的具体实现过程如图1所示。将CCD相机采集的彩色图片进行灰度化处理,利用基矩阵aω和差异矩阵均值mω计算得到差异矩阵bω；然后,计算疵点因子ε,与差异矩阵内像素比较后得到二值图像矩阵th;最后，通过中值滤波得到图像矩阵I*。

图 1 防羽布疵点检测过程Fig.1 Down-proof fabric detection process

2 结果与分析

算法运行软件环境PyCharm2018,通过Python语言编写,使用Intel(R) Pentium(R) CPU G4600 @3.60 GHz处理器。实验样本采用工厂实际生产的防羽布图像。实验环境:光源为D65光源和日光,照射方式为垂直照射和分散式照射;相机采用工业CCD相机,分辨率为2 056×2 056;相机与样本采用垂直拍摄,间距为20 cm。本文算法针对防羽布进行结构类型疵点检测,色差疵点不作为本研究的主要内容。工业CCD面阵相机采集RGB图像，是为进行随后的色差疵点检测。

使用准确率及误检率作为算法检测效果的评价指标。准确率及误检率定义为

为验证算法检测效果的有效性,选择无疵点样本846个，破洞样本439个，边撑疵样本387个，断纱样本501个,极光样本364个，划伤样本511个，使用准确率和误检率指标来评价算法检测效果，检测结果如表1所示。

表 1 疵点检测准确率和误检率统计结果Tab.1 Defect detection accuracy and false detection rate %

从表1中可直观看出,本文算法对防羽布各类疵点具有良好的检测效果,可较为准确判断织物疵点。虽然对于极光类型疵点的检测准确率最低,但也在92%以上。由表1可得本文算法对防羽布疵点检测平均准确率为95.37%,平均误检率为3.63%。

选取图像差异矩阵均值、图像均值不同的4类图像,分别记为a，b，c，d;各取89个样本,当c为不同数值时，4类图像检测的准确率如图2所示。

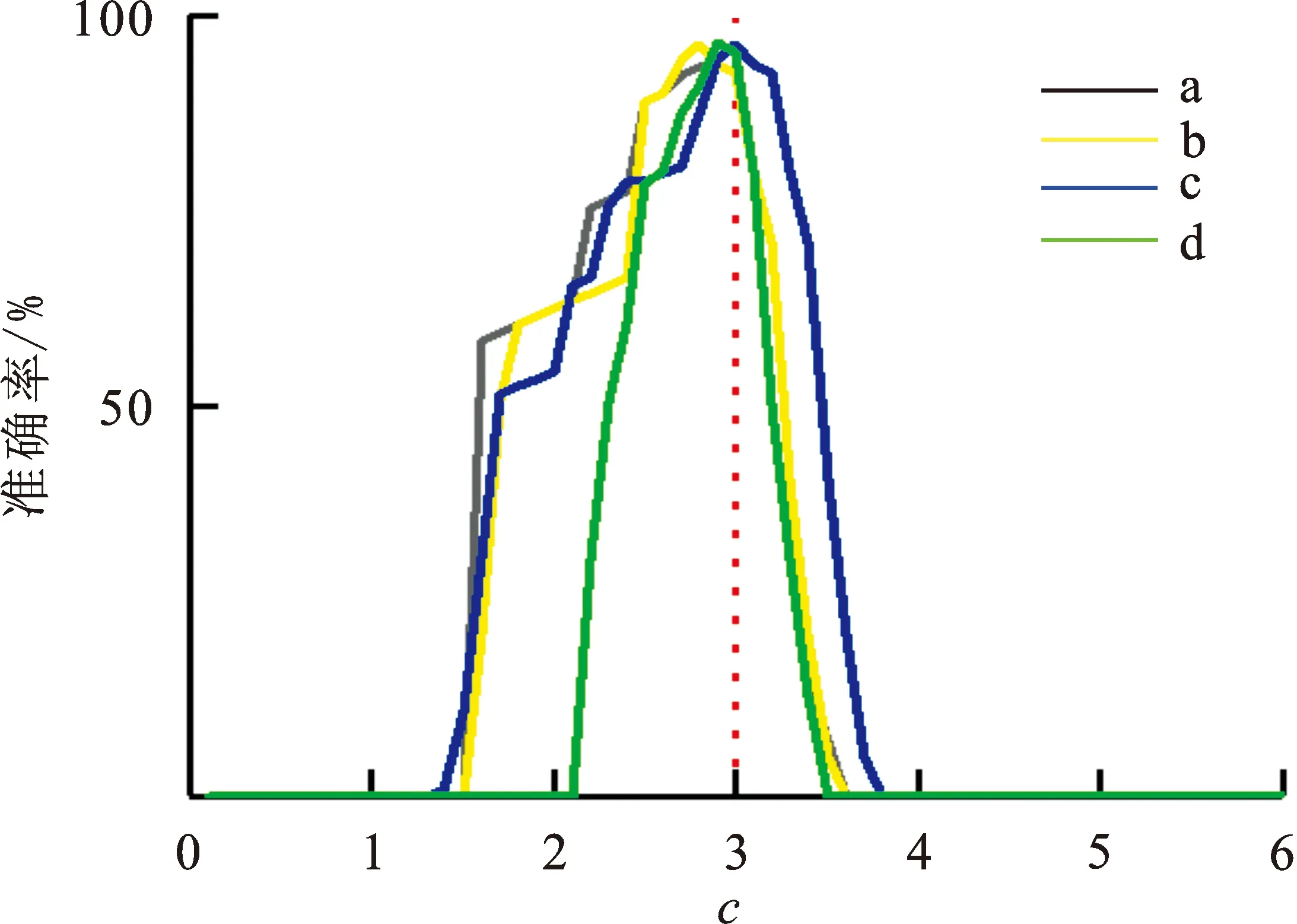
图 2 常数c与检测准确率关系Fig.2 Relationship between constant c and detection accuracy

从图2可得,对于不同均值和不同差异矩阵均值的防羽布疵点图像,当常数c=3时,检测结果都具有较高的准确率。故将c=3,带入式(6),进行后续计算。

为进一步验证算法的有效性,选择有破洞、边撑疵、断纱、极光和无疵点5种类型织物,采用另外3种疵点检测算法与本文算法对比实验效果,其中包括基于灰度共生矩阵(GLCM)的方法、基于傅里叶变换的方法和基于Gabor变换的方法。实验结果如表2所示。

表2疵点检测统计结果

Tab.2 Defect detection results

从表2可直观看出，基于灰度共生矩阵的检测算法对防羽布断纱和划伤效果较为明显,而对于破洞、色点以及无疵点图像检测的准确率偏低;基于傅里叶变换的检测算法在防羽布细小疵点和反光较为明显的图像中,检测的准确率偏低;基于Gabor的检测算法对于防羽布上有明显疵点和无疵点图像的检测效果较好,但是其抗干扰能力偏低;本文算法具有较高的抗干扰能力,能够消除复杂环境对疵点检测的影响,并且对防羽布疵点检测具有较高的准确率。其他3种算法检测效果鲁棒性不强,主要是因为防羽布质地柔软平滑易出现反光和褶皱现象影响检测结果，以及算法参数设定不够精准等原因造成。

3 结 语

对于防羽布这种高密度、柔软平滑的纺织物,经典的疵点检测算法很容易将光照与布面不平整等噪声在检测时误识别为疵点。本文提出的防羽布疵点检测算法,主要通过比较区域内像素的变化差异判断疵点。由于非疵点噪声在区域内像素变化是非突变的,而疵点是突变的,通过该特性,可以有效的区分反光、褶皱的影响,并且能够较准确地从织物图像中定位出疵点区域的位置。相比于其他疵点检测算法,本文提出的算法针对性强、准确率高，因而更具有实际应用价值。但本文算法在时间的优化和对其他纺织布品的检测效果等方面,还有待进一步研究。