一种无标定视觉伺服系统的快速跟踪策略
2020-04-08马树军金铁铮王英蕾白昕晖
马树军, 金铁铮, 王英蕾, 白昕晖
(东北大学 机械工程与自动化学院, 辽宁 沈阳 110819)
视觉伺服利用视觉传感器间接检测目标物体和机械臂的实际位姿或相对位姿,并以此实现机械臂对目标物体的跟踪或定位控制.传统的视觉伺服系统作业前需要精密的标定以获得机械臂系统和视觉系统参数,如相机标定、手眼标定、机器人标定等.标定过程精密繁琐,在一些特殊情况下几乎不可能完成.相比之下,无标定视觉伺服无需预先进行系统标定,通过对控制律的研究来控制机械臂运动,在控制成本、控制时间、便捷性和性能等方面表现更优良.在自动化、智能化的发展趋势下,无标定视觉伺服无疑拥有更大的发展潜力[1-3].
视觉跟踪控制涉及领域众多,包括机器人学、图像处理、控制理论、计算机技术等多个领域,一直以来受到各领域学者及工业界的广泛关注.按照跟踪目标是否运动,视觉跟踪可以分为静态目标跟踪和动态目标跟踪两类.其中,静态目标跟踪可以视为速度为零的动态目标跟踪.

本文从提高动态目标跟踪的时间效率出发,考虑图像特征提取频率和提取时间对跟踪效率的影响,提出了一种新的跟踪策略.
1 传统跟踪策略与新跟踪策略
雅克比矩阵描述图像特征变化速度与关节角变化速度之间的关系.计算雅克比矩阵的算法有很多,如动态Broyden算法、RLS算法、BP算法、卡尔曼滤波法等[4-6].由于传统跟踪策略和新跟踪策略均可以应用不同的算法计算雅克比矩阵,本文在介绍无标定视觉伺服跟踪策略时,以RLS算法为例.
图1为机械臂与目标相对位置示意图.如图所示,在传统跟踪策略中,机械臂末端位置θk+1由目标位置Objk计算而来.机械臂由θk运动至θk+1,末端位置接近Objk.但此时,目标已由Objk运动到Objk+1,并非停留在Objk处.运动后末端位置滞后于目标实际位置.尽管重复该过程,末端与目标距离越来越小直至成功跟踪,但是仍损失了跟踪的时间效率.

图1 机械臂与目标相对位置示意图
假设以下不等式成立
tfc≤nΔt.
(1)
式中:tfc为进行一次特征提取和计算的时间;Δt为图像捕捉时间间隔;n为使式(1)成立的最小正整数.
表1为两种跟踪策略的算法流程,其中:θk为第k次迭代时的机械臂关节角向量;Jk为第k次迭代时的雅克比矩阵;fk为第k次迭代时的目标函数;Pk为遗忘因子比例矩阵;λ为遗忘因子常数[4].

表1 两种无标定视觉伺服跟踪策略流程
定义机械臂1个图像捕捉间隙Δt所走的关节角向量θΔt,如式(2)所示.其中,ωmax为关节运动速度;θk+1-θk=[Δq1,…,Δqn]T;θk+1-θk所有元素中绝对值最大的元素为Δqmax.
(2)
为提高跟踪效率,一方面,新跟踪策略控制机械臂不停歇地以ωmax运动,以保证机械臂的跟踪速度;另一方面,控制系统使用尽可能新的图像计算关节角,以提高系统的实时性.
为了最大限度使用实时图像信息,每获取n张图像进行一次特征提取和计算.系统特征提取和计算用时tfc,机械臂运动nθΔt用时nΔt.由于控制器根据特征提取和计算结果控制机械臂运动,故nΔt时间内,无法完成上述两行为.若每获取2n张图像进行一次特征提取和计算,以下方法可完成任务.一方面,若计算结果θk+1距离θk过远,等比例缩小θk+1-θk的数值,以提高特征识别和计算的频率;另一方面,在计算结果θk+1的基础上,预测nθΔt的关节角,由于θk+1+nθΔt不依赖于下一次的特征提取与计算结果,所以,机械臂由θk+1运动至θk+1+nθΔt的过程可与下一次的特征提取与计算行为同时进行.
2 仿真实验结果
2.1 仿真实验介绍
如图2所示,使用Machine Vision Toolbox[8]和Robotics Toolbox[9]建立ABB IRB1200机械臂模型和CentralCamera相机模型,并在Matlab软件中编写不同策略控制程序,基于此建立仿真环境.其中:机械臂模型的D-H参数如表2所示;相机配置为1 024×1 024像素,焦距8 mm,像素尺寸10 μm;使用RLS算法计算关节角;ωmax设置为16.5 (°)/s;相机图像捕捉速度30 帧/s,即Δt为1/30 s;特征提取时间为25 ms,计算时间3.3 ms,即tfc等于28.3 ms.

图2 机械臂模型和相机模型
根据传统跟踪策略和快速跟踪策略构建两个无标定视觉伺服系统,控制机械臂的第二、第三关节在世界坐标系的XOZ平面追踪目标物体.目标物体分别沿式(3)描述的直线运动和式(4)描述的圆形运动.为了模拟现实情况,在仿真实验中,为观测数据添加均值为0、方差为1的高斯白噪声.
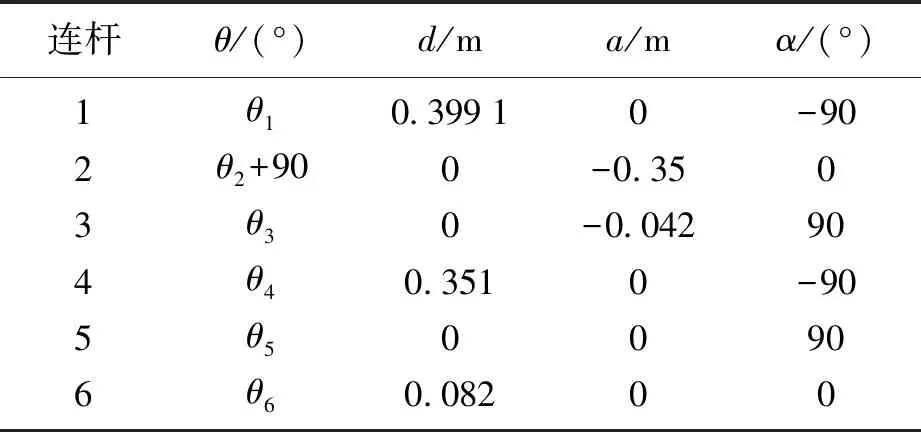
表2 ABB IRB1200 D-H参数表
注:θ为关节角;d为连杆偏距;a为连杆长度;α为连杆扭转角.

(3)
(4)
2.2 仿真实验结果
图3a和图3b分别表示目标沿式(3)和式(4)描述的曲线运动时,观测噪声方差σ2=1条件下,不同策略的跟踪轨迹.图3a中,目标由图左上角向右下角方向运动;图3b中,目标沿图中顺时针方向运动.
传统策略轨迹和新策略轨迹由起始点到第一个拐点之间的轨迹重合.该轨迹表示机械臂由θ0运动到θ1的末端轨迹.θ0,θ1为RLS算法计算的初始关节角,由于两种策略初始关节角相同,所以此段轨迹重合.

图3 不同策略跟踪轨迹图
由图3可知,新策略的轨迹比传统策略的轨迹短;新策略的轨迹方向不停向目标运动方向缓慢变化,传统策略的轨迹方向在拐点处大幅变化,在两拐点之间轨迹方向几乎不变.新策略轨迹不停向目标运动方向运动,证明新策略相比于传统策略有更好的实时性.
相比于新策略,传统策略的跟踪轨迹在目标轨迹附近有明显波动,新策略的跟踪轨迹接近目标轨迹后与目标轨迹近似重合,无明显波动.通过估计得到的初始雅克比矩阵[10]并不精确,而不同的算法每次计算都会修正雅克比矩阵.因此,随着计算次数的增加,雅克比矩阵越来越精确,计算出的关节角对应的末端位置与目标位置的误差越来越小.传统策略在每个轨迹拐点处计算一次雅克比矩阵和关节角;新策略最大移动2θΔt便进行一次计算,雅克比矩阵不精确带来的误差只作用在新策略跟踪轨迹的起始几步的一小段距离,影响极小,在轨迹图上无法分辨.传统策略初始移动距离长,受雅克比矩阵估计误差影响大,初始移动时机械臂末端超出相机视野范围风险大.
传统策略轨迹与目标轨迹近似重合后,传统策略轨迹和新策略轨迹之间无显著差别.这是因为此时机械臂末端与目标非常接近,机械臂每次移动的关节角较小.而当|θk+1-θk|≤2nθΔt时,新策略与传统策略相同,所以此部分轨迹无显著差别.
图4a和图4b分别表示目标沿式(3)和式(4)描述的曲线运动时,观测噪声方差σ2=1条件下,不同策略下机械臂末端和目标之间的距离-时间曲线.
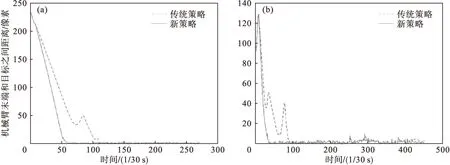
图4 不同跟踪策略机械臂末端和目标之间距离-时间曲线
图4中,初始时,新策略与传统策略曲线完全重合;随后,新策略曲线用更短的时间收敛;传统策略曲线经过几次波动后达到收敛位置.两策略曲线均收敛后,两曲线变化规律相似.
设某时刻机械臂末端和目标在像素平面上的坐标分别为(uend,vend),(uobj,vobj),机械臂末端和目标之间距离d为
(5)
表3记录了机械臂末端与目标之间距离由起始到第一次小于一个像素的时间,记为收敛时间.每种情况重复10次实验并取平均值,记录收敛时间.由表3可得,相比于传统策略,当系统应用新策略且目标沿着式(3)所描述的直线运动时,收敛效率提升了约46%;跟踪沿式(4)圆形运动的目标时,收敛效率提升了约60%.证明了新策略收敛的快速性.

表3 收敛时间统计表
3 实物实验结果
3.1 实验条件
实验设备主要包括ABB机械臂、台式电脑和Kinect v1相机,如图5所示.其中:ABB机械臂型号为IRB1200,D-H参数见表2;台式电脑CPU型号为AMD速龙200GE,运行内存8 GB;相机的图像捕捉频率为30 帧/s,分辨率为640×480.
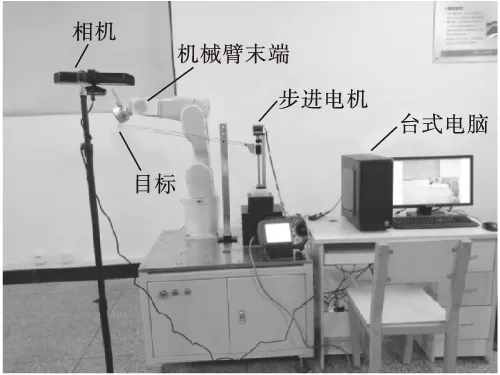
图5 实验设备
机械臂初始关节角向量θ0为[0,-5π/180]T,θ1为[π/90,-2π/45]T,单位为rad;最大关节角速度ωmax设置为21 (°)/s;初始雅克比矩阵为
一次特征提取时间约为23 ms;计算时间小于0.1 ms;一次特征提取和计算的时间和tfc约为23 ms;图像捕捉间隔Δt=1/30 s;使式(1)成立的最小正整数n为1.
3.2 实验结果
在图6a中,目标由轨迹的左上端向右下端运动;传统策略的跟踪轨迹与目标轨迹近似重合前有明显波动,新策略跟踪轨迹无明显波动.证明新策略对初始雅克比矩阵误差具有更高的抗干扰性.
在图6a中,传统策略的轨迹方向在拐点前后大幅变化,拐点之间无明显变化,其轨迹方向并非总是指向目标位置;新策略的轨迹方向一直向目标运动方向缓慢变化.图6b中,传统策略下,目标与机械臂距离有较大波动;新策略下距离近似直线减小.证明新策略相比于传统策略有更好的实时性.
在图6b中,传统策略收敛时间约为5.3 s;新策略收敛时间约为3 s;证明了新策略收敛的快速性.

图6 不同跟踪策略跟踪轨迹图及对应距离-时间曲线
4 结 语
本文提出一种新的无标定视觉伺服跟踪策略.一方面,系统通过预测机械臂关节角,使控制器行为与机械臂运动并行进行;另一方面,系统使用更实时的图像信息计算关节角.在仿真和实物实验中,通过对比跟踪时间、跟踪路径,验证了新策略的快速性、实时性和对初始雅克比矩阵误差的抗干扰性.
