后方交会解算方法选取的若干问题

蔡文豪

（广东省建筑科学研究院集团股份有限公司 广州510500）

0 引言

后方交会是摄影测量、计算机视觉等相关领域的一个基础性问题，它是通过一定的物方控制点及其在影像上对应像点的坐标反算出相机的位置与姿态（也称为相机的外方位元素）［1］。后方交会被广泛地应用于全站仪测量、三维激光扫描仪测量等测量测绘设备中。特别是在三维激光扫描的外业测量中，针对大体量的目标物体，可以采用架设两个棱镜作为标靶，并通过这两个棱镜与扫描仪的后方交会解算与不断地辗转转站方式进行扫描测量。

以某三维激光扫描外业为例介绍后方交会辗转转站测量过程。如图1所示，某双幅跨线桥由4根独柱墩A、B、C 和D 支撑横跨底部道路，为了获取该跨线段的桥梁三维模型对其进行三维激光扫描。在桥底靠近桥墩的合适位置架设两个360°棱镜HS1和HS2且始终固定不动，并在底部道路上选取5个合适位置Z1、Z2、Z3、Z4和Z5作为仪器架站位置，使这些仪器架站点均能和棱镜点HS1 和HS2 形成通视。扫描过程如下：设定第一站Z1的坐标（可以给定任意坐标值），通过仪器的全站仪功能计算出HS1 和HS2 的坐标，然后进行第1 站扫描获取第1 站点云；将仪器转站至Z2 点，由HS1 和HS2 的坐标解算出Z2 的坐标，然后进行第2 站扫描获取第2站点云；……以此类推可获取全部5站的点云。该方法获得的点云避免了内业拼接误差，具有更高的精度。但是如果在后方交会解算Z2、Z3、Z4和Z5的坐标过程中由于选取方法和选取点的不恰当，同样会形成精度较低的点云数据。因此后方交会解算方法的选取对于三维激光扫描点云的精度尤为重要。

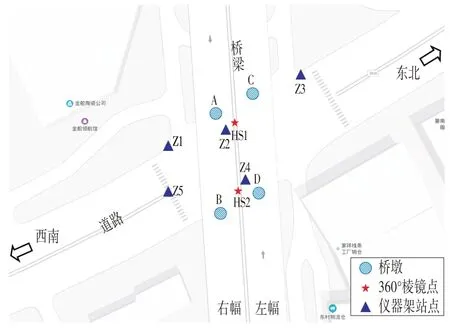
图1 采用后方交会的辗转转站三维扫描过程Fig.1 Three-dimensional Scanning Process Based on Station Tossing and Reversing Using Resection

后方交会本质上可以理解为是将影像的位置和姿态从像方坐标系归算到物方坐标系下的过程。这个过程可以看作为刚体的空间运动，即刚体的旋转运动和平移运动的组合。目前大多数学者将旋转变换采用欧拉角与四元数来表达，称为欧拉角法和四元数法［2］。但是由于欧拉角存在一些天生缺陷，在使用过程中需要特别注意。本文旨在从理论角度分析欧拉角方法是如何产生自身缺陷，并在此基础上介绍其与方向余弦阵以及四元数之间的关系，从而给出实际应用中的一些建议。

1 欧拉角

欧拉角（Euler angle）的概念最早由欧拉于1776年提出，简单来讲，它是描述三维空间任一刚体相对固定坐标系的姿态或者方位（orientation）的三个角度。对于任何一个空间物体上的随体坐标，都可以将其平移至惯性坐标系处并使二者原点重合，然后将随体坐标绕不同轴经过三次基本的旋转都可以使两个坐标系完全重合，这三次基本旋转的转动角度就是欧拉角，记为α，β，γ，绕三个轴的旋转的顺序被称为旋转顺规（rota⁃tion convention）或者旋转顺序（rotation sequence）。

众所周知，任意一个旋转或者空间方位都可以通过三个基本的绕轴旋转组合得到。对于一个拥有三个坐标轴（X，Y，Z）的欧式空间，依据排列组合知识共有33=27种可能的旋转顺规，我们可以将其分成三类：

⑴ 无效旋转顺规。凡是在相邻的两次旋转中绕同一轴旋转的顺序都是无效的，因为它们势必要削减问题的自由度［3，4］，这样的旋转顺规有 15 种：XXX，YYY，ZZZ，XXY，XXZ，YYX，YYZ，ZZX，ZZY，XYY，YXX，ZXX，ZYY，XZZ，YZZ；

⑵ 对称旋转顺规。第一次旋转轴和第三次旋转轴一致的旋转顺规，共有6 种：XYX，XZX，YXY，YZY，ZXZ，ZYZ；

⑶ 非对称旋转顺规。第一次旋转轴和第三次旋转轴不同的旋转顺规，共有 6 种：XYZ，XZY，YXZ，YZX，ZXY，ZYX。

以ZXZ旋转顺规为例来说明这一旋转过程。如图 2 所示，xyz为惯性坐标系，XYZ为随体坐标系，N是两个坐标系xy平面和XY平面的交线。在这一旋转顺序下，3个欧拉角按照如下旋转顺序获得：第一步：绕z轴旋转角度，使坐标轴x与交线N重合；第二步：绕x轴（N轴）旋转角度，使坐标轴z与Z重合；第三步：绕z轴（Z轴）旋转角度，使坐标轴x与X重合。

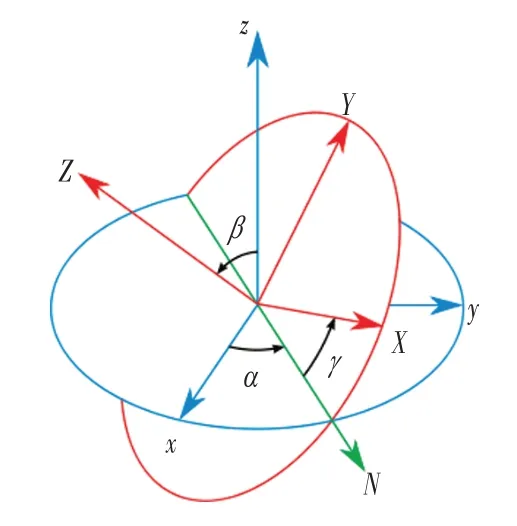
图2 ZXZ旋转顺规下的欧拉角定义Fig.2 The Definition of Euler Angles under ZXZ Rotation Convention

需要注意的是，不同的旋转顺规会得到不同的欧拉角的值，这被称为欧拉角的多值性。因此在使用欧拉角前一定要声明旋转顺规，否则所述欧拉角是无意义的。此外，注意到在上述例子中，如果一开始xy平面就和XY平面重合，即，z轴和Z轴有相同的或者相反的方向，此时将会出现奇点问题（singularity problem）——若z轴与Z轴同向，此时β=2π，（α-γ）的值是唯一确定的但是它们各自的值并不能唯一确定；反之，若z轴与Z轴反向，此时，β=π，（α-γ）的值是唯一确定的但是它们各自的值并不能唯一确定。这一奇点问题在工程应用中就变成了令人头疼的“万向节死锁”问题（gimbal lock problem）［5-7］。

综上，欧拉角方法具有多值性以及可能存在的奇点困境，因此在后方交会解算中需慎重选用。

2 方向余弦阵

方向余弦阵（direction cosine matrix，DCM）是连接像方坐标系和物方坐标系的桥梁，二者之间的坐标关系一般可表述为

其中，X 和x 分别表示像方坐标和物方坐标；T 表示两个坐标系之间的平移关系；R即方向余弦阵，为3阶方阵。由于方向余弦阵起到两个坐标系之间坐标变换的转承过渡作用，因此又被称为旋转矩阵（rotation ma⁃trix）。为了表述上的方便，对任意角度θ的正、余弦作如下简记

对于三个基本的旋转运动（elemental rotation），其方向余弦阵定义如下：

绕x轴旋转θ角度的方向余弦阵定义为：

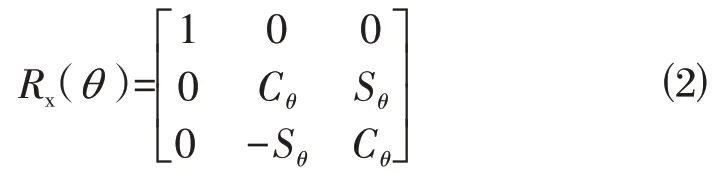
绕y轴旋转θ角度的方向余弦阵定义为：

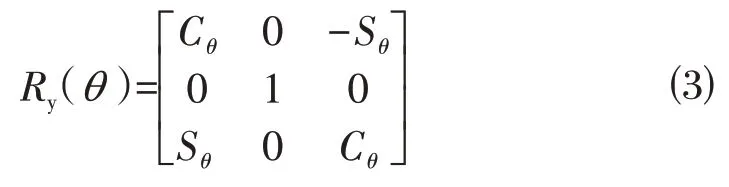
绕z轴旋转θ角度的方向余弦阵定义为：

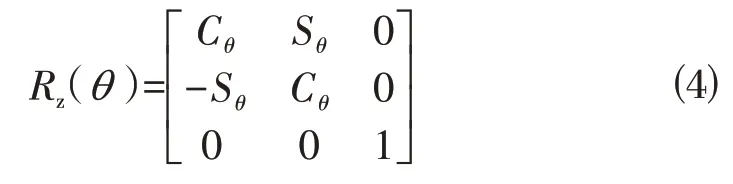
任何旋转顺规下的旋转矩阵都可以通过上述基本方向余弦阵按照矩阵左乘的规则来得到［8］，例如XYZ顺规下的方向余弦阵为：

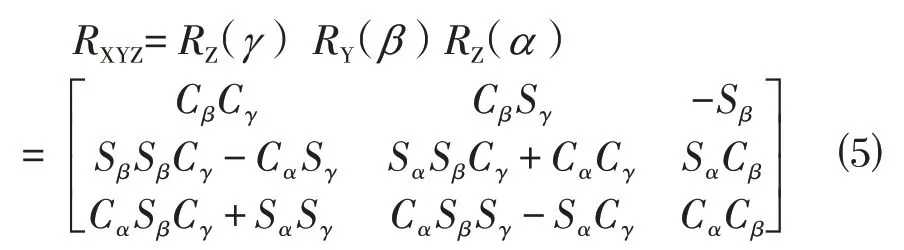
同样地，例如ZXZ顺规下的方向余弦阵则为：

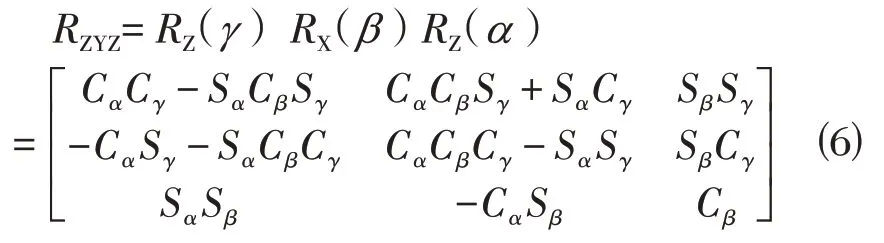
值得注意的是，虽然欧拉角在不同的旋转顺规下有数值的差别，但是方向余弦阵确是具有唯一性的，举例说明，若在XYZ顺规下的欧拉角为（α1，β1，γ1），而在ZXZ顺规下的欧拉角为（α2，β2，γ2），那么将它们分别代入式⑸和式⑹中，最终计算出来的方向余弦阵应该是相等的，即

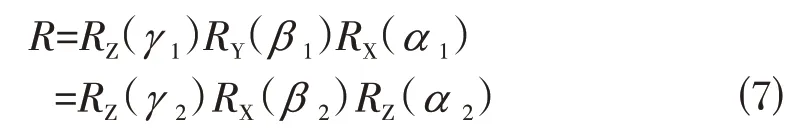
方向余弦阵的唯一性对后方交会解算具有重要作用和意义。

那么在出现欧拉角奇点的情形下，方向余弦阵是如何失效的呢？以XYZ顺规下的奇点为例说明。若β=π/2，则Cβ=0，Sβ=1，则此时的方向余弦阵为：

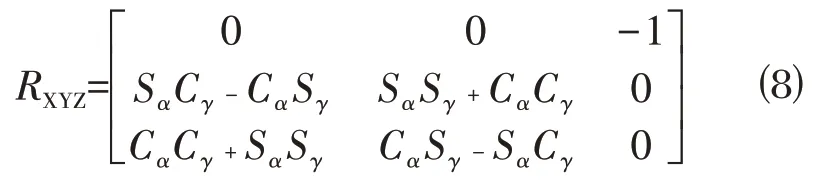
利用三角函数和差角公式，式⑻可化为：

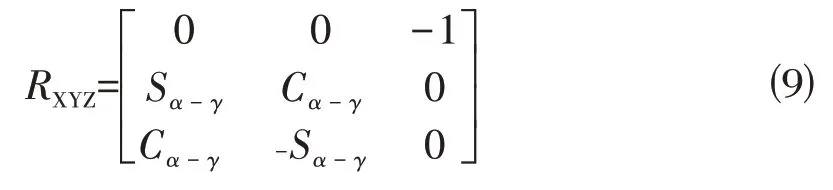
可见此时，无论（α-γ）如何变化，上述矩阵只有第一列和第二列在变化，说明此时刚体方向始终指向-Z轴，也就是说在出现欧拉角奇点的情形下，方向余弦阵将会出现自由度丢失（loss of DOF），进一步造成了方向余弦矩阵的失效。

3 四元数

在数学中，四元数是复数系经过扩充形成的一种数系，最早由爱尔兰数学家William Rowan Hamilton 于1843 年提出并将其应用于三维力学领域［9］。四元数的一个典型特征就是不满足乘法的交换律，且用其表征空间的物体的姿态（方位）具有唯一性。四元数的基本形式如下：

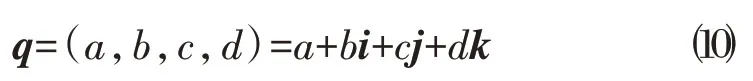
其中，a、b、c和d是实数；i，j和k是基本虚单位，这些虚单位的运算性质与笛卡尔坐标系下的三个正交坐标轴的运算性质形式上是一致的：

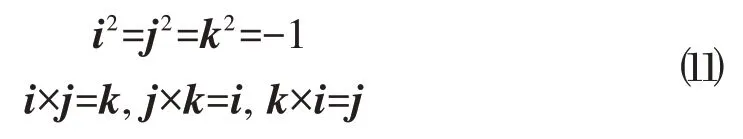
在本文第2节介绍了由欧拉角表征的方向余弦阵，而用四元数表征方向余弦阵的研究在文献［10，11］中都有详细介绍。用四元数表征的方向余弦阵形式如下：

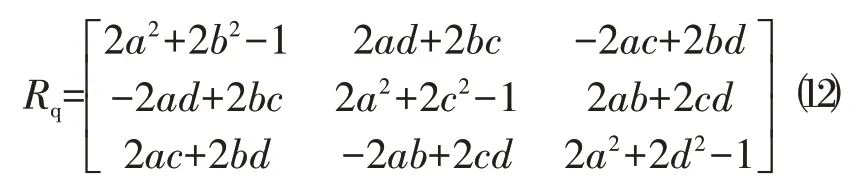
显然四元数与欧拉角之间没有一一对应的关系，但欣慰的是，对于任何一个姿态给定的空间物体，其方向余弦阵都是唯一的，即无论是用欧拉角表示的，还是用四元数表示的，还是用其他哪种形式给定的，方向余弦阵都应该有一个最终的统一的数值。这种统一的形式可以写成：

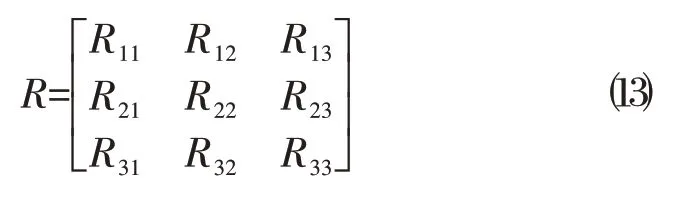
亦即，对于同一个空间姿态给定的物体，式⑸、式⑹、式⑿和式⒀最终都应该相等：

综上，无论欧拉角方法还是四元数方法都可以用来表征刚体的空间姿态并用以进行后方交会解算，并且二者最终表现出来的方向余弦矩阵形式是一致的。由于在工程应用特别是三维激光扫描作业中，其方向余弦矩阵通常很容易根据物方坐标和像方坐标求得。接下来的问题就转变成在已知空间物体姿态的方向余弦阵前提下，如何解算出相应的四元数。一种传统而直观的方法就是根据式⒀和式⒁建立四元数和与对应的方向余弦阵之间对应关系然后求解复杂的代数方程组，可以想见这种方法至少有两方面缺陷，其一是方程的数量（9个）远远大于未知数的数量（4个），其二是负数可能出现在平方根符号下面。一种行之有效的方法就是对方向余弦阵进行最优正交化处理，即可得到最优化正交矩阵［12，13］：

在这种方式下，四元数（a，b，c，d）可由式⒃计算

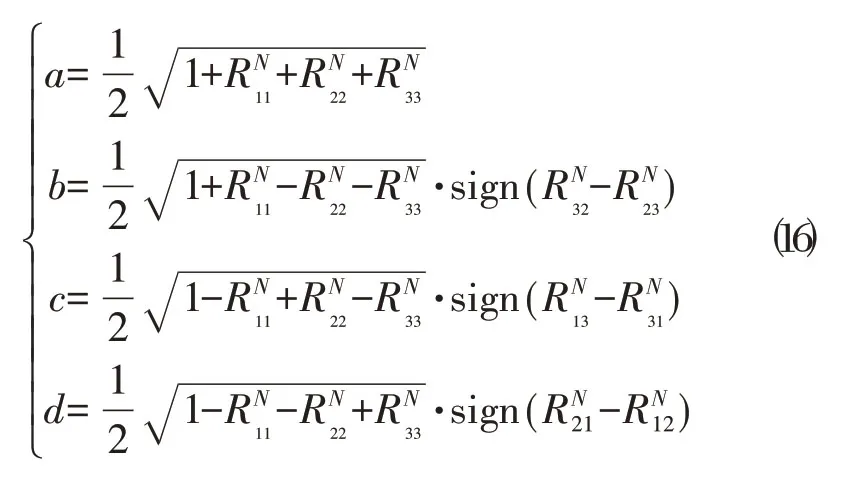
由式⒃表征的空间姿态具有唯一性，不会出现如欧拉角方法面临的奇点问题，因此该方法是后方交会解算的首选方法。

4 结语

无论是采用欧拉角方法还是四元数方法，从物方坐标到像方坐标之间转换过度的方向余弦阵的最终表达形式是唯一的，正是由于方向余弦矩阵的唯一性这一特征，我们可以建立起三者之间的关系。但是由于欧拉角存在多值性和可能存在奇点问题，而四元数方法表征空间姿态具有唯一性。因此在后方交会解算过程中应尽量避免使用欧拉角方法，而尽量采用四元数方法。