Matlab在化学领域中的应用
2020-04-07窦立岩汪丽梅
窦立岩,汪丽梅
(吉林建筑大学,吉林 长春 130018)
Matlab语言是国内大学电子信息和通信工程类专业必修的工具基础课,但从其产生及发展的历程来看,强大的数据分析处理能力更能体现其核心价值,因此,Matlab的应用范围绝不仅仅局限于某些目前比较热门的学科领域,而应该作为一种用途广泛的常用工具软件加以推广。本文旨在从基础化学本科教学的内容中列举一些实例来阐述Matlab的辅助教学作用。目前化学本科教学的基础内容包括无机、有机、分析、物理化学、物质结构及相关实验内容,除无机和有机主要涉及结构反应外,其他几门课程都包括大量的计算和实验数据处理,在已基本保证学生人手一台笔记本电脑的基础上,把Matlab软件纳入到必备学习工具软件的范畴里,提高学生利用现代工具的能力,将进一步靠近高校当前的培养目标。
1 实例分析
1.1 分析化学
实例1:草酸在水溶液中存在的形式是:H2C2O4, HC2O4-, C2O42-, 已知Ka1=5.9e-2,Ka2=6.4e-5,请绘制出HC2O4-在不同pH值下分布曲线图。
Matlab程序如下:
Ka1=5.9e-2;
Ka2=6.4e-5;
pH=0:0.1:7;
H=10.^(-pH);
d1=Ka1*H./(H.^2+Ka1*H+Ka1*Ka2);
plot(pH,d1);
xlabel('pH值');
ylabel('分布系数');
title('分布曲线')
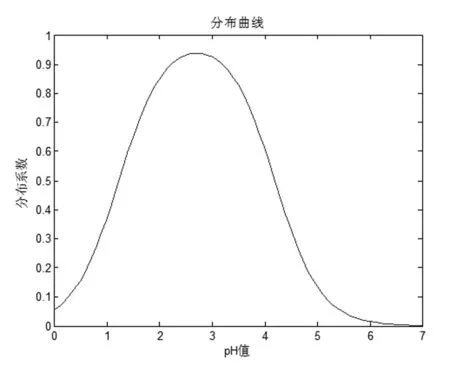
图1 HC2O4- 在不同pH值下分布曲线
从上例可以看出,通过简短的Matlab语句表达,就可以将HC2O4-随pH值的变化规律以曲线的形式清晰的展示出来,而且任意pH值下的分布系数也都可以获取,体现了强大的数据处理能力。
1.2 物理化学
实例2:某温度下乙醛分解反应为C2H4O(g)→CH4(g)+CO(g),根据以下数据判断其反应级数。

表1 乙醛浓度与时间对应关系

表2 乙醛浓度与反应速率对应关系
将(1)式两端取对数得:lnr=lnk+nlnC,随之可使用Matlab继续解题,语句如下:
c=[5.85,4.46,3.83,2.81,2.01];c=log(c)
r=[0.013,0.010,0.006,0.004,0.002];
r=log(r);
p=polyfit(c,r,1);
ci=linspace(log2.0,log6.0,50);
ri=polyval(p,ci);
plot(c,r,'o',ci,ri,':')
xlabel('logc');ylabel('logr')
p
回车后运行:
p =
1.7833 -7.4197
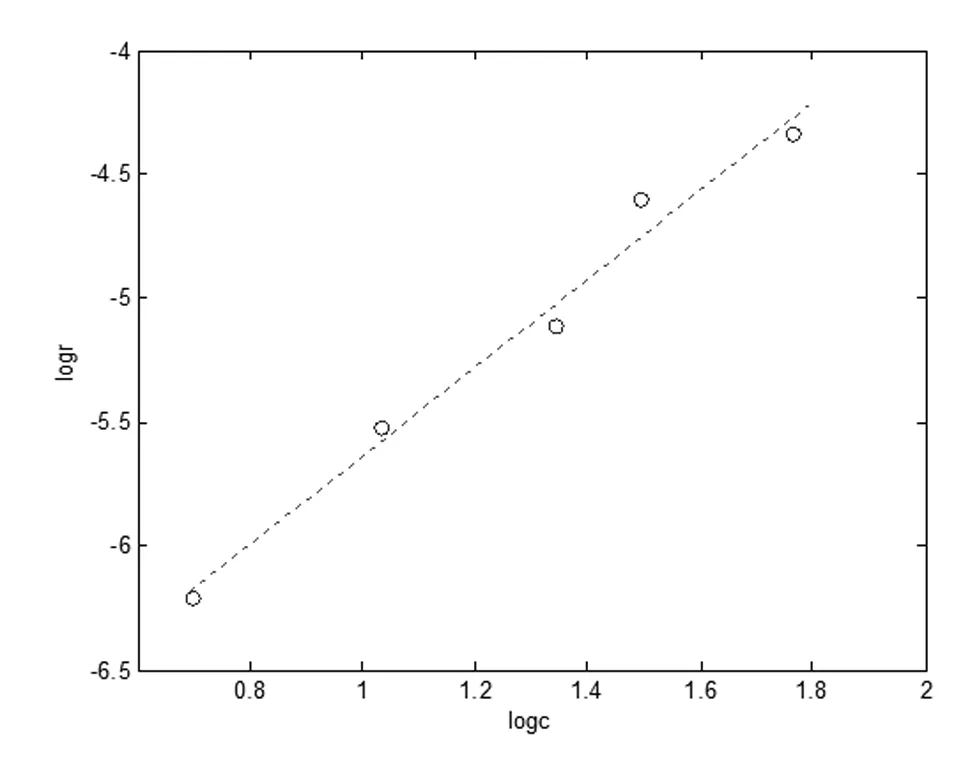
图2 乙醛反应速率与浓度对数关系
舍掉负值后得p(斜率)=1.7833,故判断反应级数为2级。
在本例中遇到一个非常重要的Matlab函数,polyfit即拟合函数,它的作用是可以把若干获得的已知数据进行处理,最终达到拟合到一条函数曲线上的目的,相当于根据数据的变化规律来建立相应的数学模型。对于本例,该法有些大材小用,因为仅仅是一级拟合,如有大量数据需要处理,而且对拟合精度有很高要求,需进行多项式拟合,人工计算是无论如何都不能比拟的。与拟合函数同等重要的另外一个函数是插值函数,命令通常为interp1,即一维插值,与拟合函数不同,插值函数除一维插值外,还包括其他插值方式,如二维插值、N维数据插值、三次样条插值等,其中以一维插值最为常用,示例如下:
实例3: 某检测参数w随时间采样结果如表3所示,用数据插值法求出t=3,18,26时的w值。
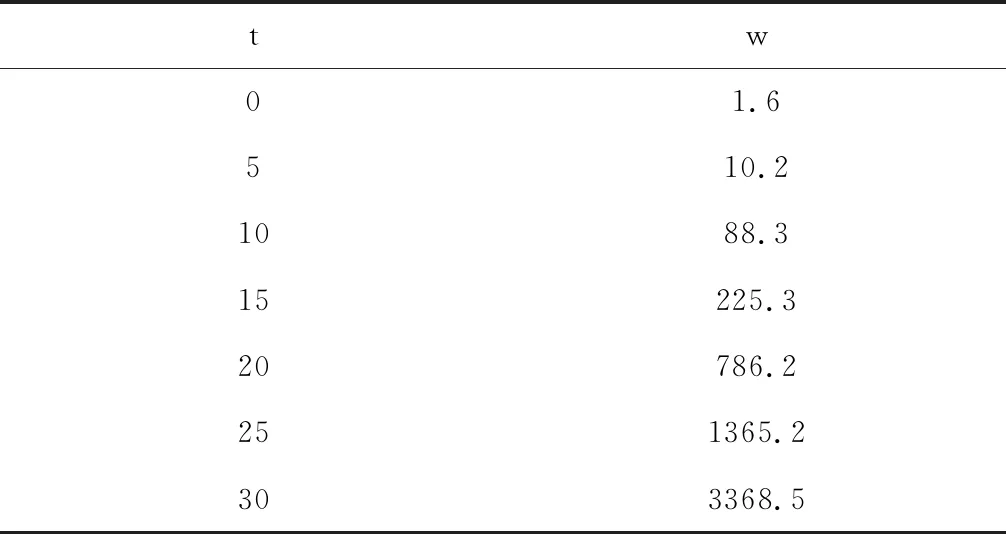
表3 参数w随时间采样结果
Matlab语句如下:
t=[0,5,10,15,20,25,30];
w=[1.6,10.2,88.3,225.3,786.2,1365.2,3368.5];
X=[3,18,26];
w1=interp1(t,w,X);
w1
回车后运行结果:
w1 =
1.0e+003 *
0.0068 0.5618 1.7659
不难看出,利用插值方法可以得到此时间范围内所有对应结果,前提是要获取若干采样结果,从而找到其变化规律,实际上这里面已经暗含了拟合的过程,因此插值可以看作是数据拟合基础上的进一步应用。
1.3 物质结构
Matlab语句如下:
r=0:1:500;
a0=52.9;
a=sqrt(1/pi*a0^3).*exp(-r/a0);
Dr=4*pi*r.^2.*a.^2;
plot(r,Dr,'-*b');
xlabel('核外半径')
ylabel('电子出现概率')
title('基态氢原子径向分布函数图')
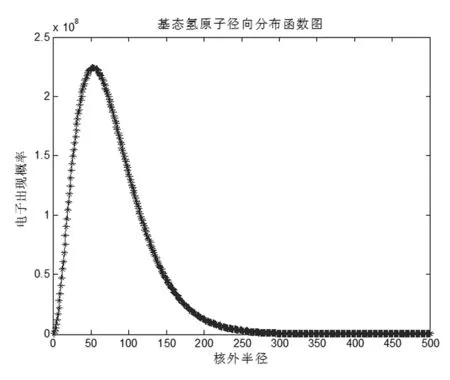
图3 电子出现概率与核外半径关系
本例从功能方面来看,与实例1并无区别,都体现了计算和数据处理能力,但从计算量来看要大得多,说明Matlab完全可以处理更加复杂的计算,而对于物质结构这类研究微观领域电子云分布函数涉及到大量复杂公式的科学,正可作为Matlab软件用武之地。
2 结语
Matlab在国外早已成为流行的学习工具软件,其受欢迎之处不仅在于其功能几乎覆盖了目前所有的重要科技领域,而且是入门极易的一门语言,短期的学习即可掌握其基本语言。对于化学领域的工作者来说,一旦具备了利用Matlab进行计算及数据处理能力,使许多抽象的公式以图形曲线的形式展现出来,不仅会对问题的理解更加直观,而且也增添了趣味性,尤其是学生平日的学习也能培养出善于乐于使用Matlab解答学科问题的习惯,对于其日后发展将产生不可估量的作用。
