多线预应力混凝土斜拉桥上无缝线路纵向受力与变形

张鹏飞 耿琦慧 桂昊

（华东交通大学铁路环境振动与噪声教育部工程研究中心，南昌 330013）

随着桥梁技术的发展，斜拉桥在铁路中的应用逐渐增多，尤其在跨越宽阔的峡谷、河流和海峡时被广泛采用。斜拉桥是自锚式体系，斜拉索承受的水平分力使主桥连续梁受压，在施加荷载前后，桥梁结构的形状及轴线有较大变化；同时，斜拉桥是高次超静定结构，为“塔-索-梁”空间结构组合体系，具有强非线性，因此，斜拉桥结构各部件之间的力学传递机理较为复杂。研究大跨度斜拉桥上无缝线路纵向受力与变形规律时，需要充分考虑斜拉桥结构体系的特点，这增加了大跨度斜拉桥上无缝线路研究的难度［1］。

与一般桥上无缝线路相比，大跨度斜拉桥上无缝线路的力学传递机理、计算模型、计算参数及设计荷载的取值有很大差异，国内外学者对此做了大量的研究。蔡小培等［2］建立了大跨度斜拉桥上无缝线路空间耦合模型，分析了斜拉桥上无缝线路各结构间的相互作用和力学行为，对调节器设置方案进行了优化。闫斌、戴公连［3-4］用带刚臂的梁单元模拟斜拉桥主梁，用非线性弹簧模拟线路纵向阻力，建立“塔-索-轨-梁-墩-桩”空间耦合有限元模型，分析了纵向力对斜拉索和塔墩的影响，讨论了桥梁截面形式、斜拉桥约束方式、线路纵向阻力模型、主梁和拉索温度变化、风压、伸缩调节器的位置等参数对纵向力的影响。赵卫华等［5］建立了模拟半漂浮体系的平面模型，分析了主塔刚度、斜拉索刚度和黏滞阻尼器对制动力的影响，并提出了制动力的简化算法。徐浩等［6］以钢桁斜拉桥为例，建立了斜拉桥上无缝线路纵向力计算模型，分析了斜拉索和主塔墩温差、主塔墩和主梁刚度以及支撑体系对钢轨伸缩力的影响。王平等［7］建立了斜拉桥上无缝线路纵向力计算模型，并编制软件计算钢轨伸缩力，计算时将斜拉桥简化为跨中设置固定支座的连续梁。丁静波等［8］基于有限元刚度法建立无缝线路附加纵向力简易模型，直接加载位移，并利用梁、轨相对位移与纵向阻力间的关系，计算特殊桥梁结构无缝线路各种附加纵向力。

本文在既有研究的基础上，基于有限元理论并结合实际工程，充分考虑斜拉桥上无缝线路、有砟轨道、梁体、主塔、斜拉索及桥墩之间的相互作用，建立4线预应力混凝土斜拉桥上无缝线路空间模型，分析在温度荷载、列车荷载及制动荷载作用下大跨度斜拉桥上无缝线路纵向受力与变形特点。

1 有限元模型及计算参数

1.1 工程概况

某4线铁路跨越宽阔河流时采用（130+260+130）m双塔预应力混凝土斜拉桥，桥上铺设有砟轨道。主梁为预应力混凝土结构，采用单箱三室变高度整体箱形截面，中支点处最低点梁高13 m，跨中及边支点处最低点梁高6 m。斜拉索锚固点纵向间距8 m，每个桥塔单侧各设10根斜拉索。主桥墩采用双肢薄壁墩，双柱中心间距6.4 m，净间距4.0 m，墩高25.5 m。

1.2 有限元模型

以该4线双塔斜拉桥为例，基于有限元法建立斜拉桥上无缝线路空间模型。为了消除边界效应，在主桥两侧分别选取5×32 m简支梁和100 m路基段进行建模。

1）主梁和简支梁均为C60预应力混凝土结构，采用solid45实体单元模拟。主梁为变截面连续梁，其截面参数均按实际工程尺寸选取。

2）采用beam188单元模拟60 kg/m钢轨；桥墩与桥塔均采用beam189单元模拟。beam189单元包含有应力刚度，默认情况下应力刚度使元素能够进行弯曲、侧向弯曲和扭转稳定性分析。

3）斜拉索采用combin14弹簧单元模拟，斜拉索垂向刚度和纵向刚度均为70 kN/mm；边墩支座采用弹簧进行模拟；简支梁的墩顶纵向刚度为350 kN/mm。

4）扣件采用非线性弹簧单元模拟，扣件横向刚度和垂向刚度分别取50，35 kN/mm。线路采用Ⅲ型混凝土轨枕，线路纵向阻力采用非线性弹簧单元模拟。道床阻力变化如图1所示。

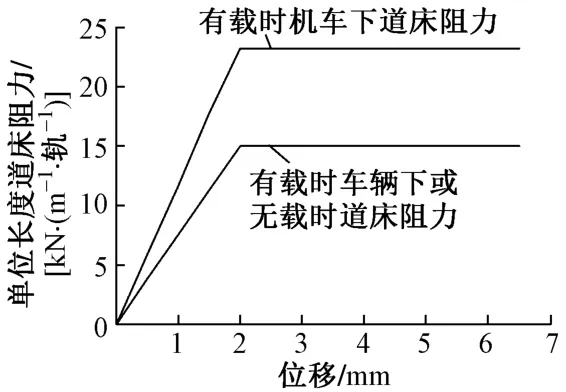
图1 道床阻力

斜拉桥上无缝线路结构如图2所示。“塔-索-梁-轨”空间耦合有限元模型如图3所示。斜拉桥连续梁端部横断面及线路布置如图4所示。

图2 斜拉桥上无缝线路结构示意

图3 空间耦合有限元模型

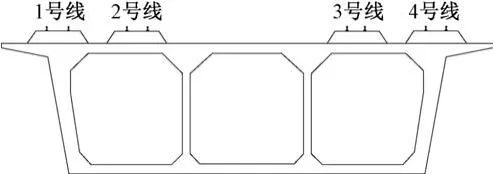
图4 连续梁端部横断面及线路布置

1.3 荷载参数

1）温度荷载

在计算钢轨伸缩力时，文献［9］中规定按梁日温差考虑。本文在计算钢轨伸缩力及位移时考虑梁体及桥塔日升温20℃。

2）列车荷载

桥上无缝线路挠曲力和制动力采用静荷载计算，不考虑冲击系数。列车荷载取ZK标准荷载中的均布荷载，为64 kN/m。

3）制动荷载

制动荷载集度q计算式为

式中：μ为制动率，取0.164；Qd为设计荷载，采用ZK标准荷载中的均布荷载，取64 kN/m。

由式（1）计算得到q=10.5 kN/m。加载长度一般取400 m。

1.4 模型验证

斜拉桥结构复杂，计算难度较大，为了验证本文模型及计算参数的正确性，对比了与本文类似的斜拉桥上有砟轨道无缝线路的计算结果。

文 献［10］以［2×23.8+3×31.7+（48+96+48）+31.7+23.8］m预应力混凝土斜拉桥为例，将梁体和桥塔日降温20℃以计算钢轨伸缩力，得到梁轨最大相对位移为17.2 mm，钢轨最大伸缩力为574.96 kN（见图5）。为了验证本文模型的正确性，采用与文献［10］相同的工况进行计算，得到日降温20℃时钢轨伸缩力，见图6。由于本文主梁跨度要大于文献［10］的主梁跨度，因此本文计算结果与文献［10］结果有偏差，但伸缩力和梁轨相对位移的变化趋势较为吻合，验证了本文模型的可靠性。

图5 文献［10］钢轨伸缩力

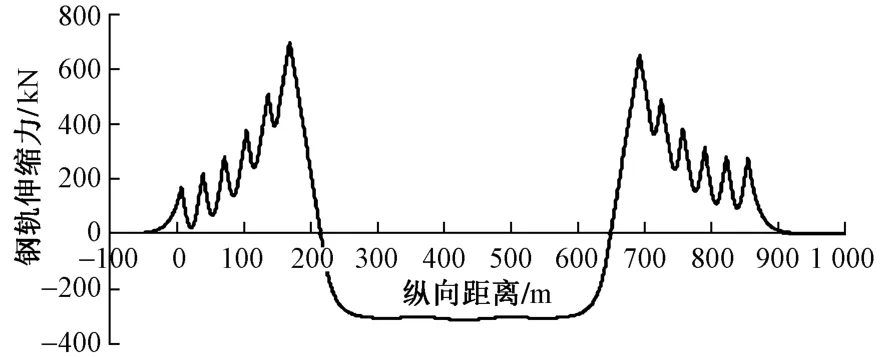
图6 本文钢轨伸缩力

2 伸缩力计算分析

为分析大跨度斜拉桥在温度荷载作用下的纵向受力与变形情况，本文设计了3种工况：工况1为梁体、桥塔同时日升温20℃；工况2为梁体日升温20℃；工况3为桥塔日升温20℃。计算得到钢轨伸缩力及位移，见图7，钢轨伸缩力与位移的最值见表1。

图7 钢轨伸缩力及位移

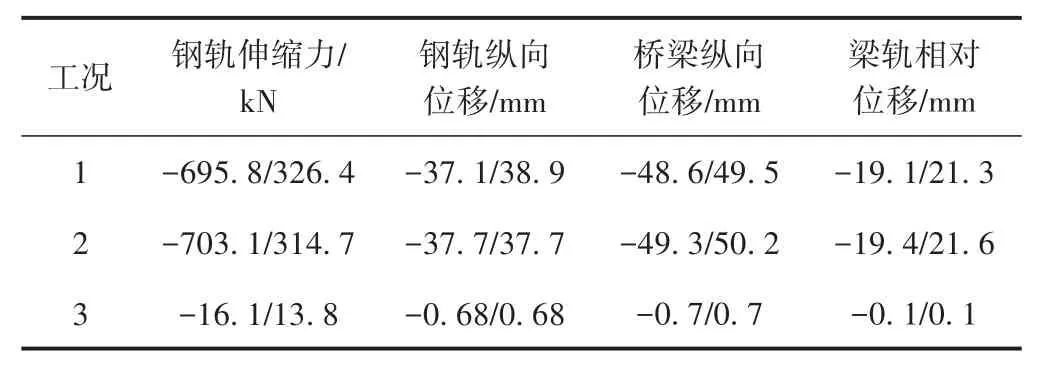
表1 各种工况下钢轨伸缩力与位移最值

从图7可知，工况3下钢轨伸缩力与位移无明显变化，这是因为桥塔升温变形主要表现为垂向，而钢轨的伸缩力主要由梁体变形引起，钢轨与主梁在温度荷载作用下的受力与变形几乎与桥塔无关；对比工况1与工况2发现，这2种工况下钢轨伸缩力数值相差不大，变化趋势相近；工况1数值比工况2略小，这主要是由于桥塔的存在对梁体有一定的约束作用，所以3个工况中工况2钢轨伸缩力幅值最大；钢轨伸缩力最大幅值出现在连续梁两端与简支梁连接处，并在简支梁梁缝处出现峰值；在连续梁中部一定范围内梁轨相对位移为0，所以这一范围内钢轨伸缩力几乎没有变化；桥梁纵向位移及梁轨相对位移的最值都出现于连续梁和简支梁连接处。

从表1中看出，钢轨伸缩力与位移的最大幅值均出现在工况1或工况2时，钢轨伸缩力最大幅值为703.1 kN；钢轨纵向位移最大幅值为38.9 mm；桥梁纵向位移最大幅值为50.2 mm。

3 挠曲力计算分析

进行挠曲力计算时列车荷载取64 kN/m。列车荷载加载在1号线上（位置参见图4），从左侧主桥墩处向右施加400 m（参见图2），约16节动车组的长度。钢轨挠曲力及钢轨纵向位移计算结果见图8，各线钢轨挠曲力及钢轨纵向位移的最值见表2。

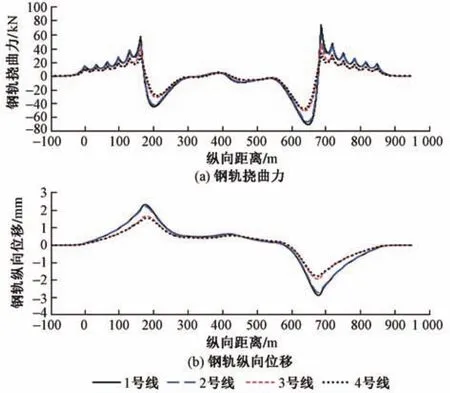
图8 钢轨挠曲力及钢轨纵向位移

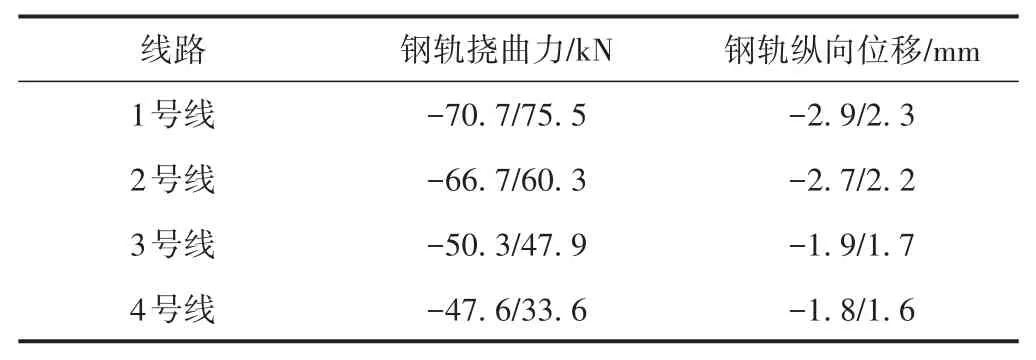
表2 各线钢轨挠曲力与钢轨纵向位移最值

由图8及表2可知，钢轨挠曲力在连续梁两端出现突变，挠曲力最大幅值出现在连续梁端部附近；钢轨在连续梁部分受压，简支梁部分受拉；由于加载位置的不对称，钢轨挠曲力与钢轨纵向位移呈不对称分布；相比于施加荷载的1号线，其他线路的钢轨挠曲力与钢轨纵向位移随着距1号线距离的增大而逐渐减小；1号线与2号线距离较近，所以1号线与2号线钢轨挠曲力与钢轨纵向位移相差不大；相比1号线，2号线钢轨挠曲力最大幅值减小5.7%，3号线减小28.9%，4号线减小32.7%；相比1号线，2号线钢轨纵向位移最大幅值减小6.9%，3号线减小34.5%，4号线减小37.9%。

4 制动力计算分析

本节分析在斜拉桥上列车紧急制动时钢轨产生的制动力，计算时不考虑温度荷载及列车荷载的影响。制动荷载加载于1号线，从左侧主桥墩位置向右加载400 m。钢轨制动力与钢轨纵向位移计算结果见图9，钢轨制动力与钢轨纵向位移最值见表3。

图9 钢轨制动力及钢轨纵向位移

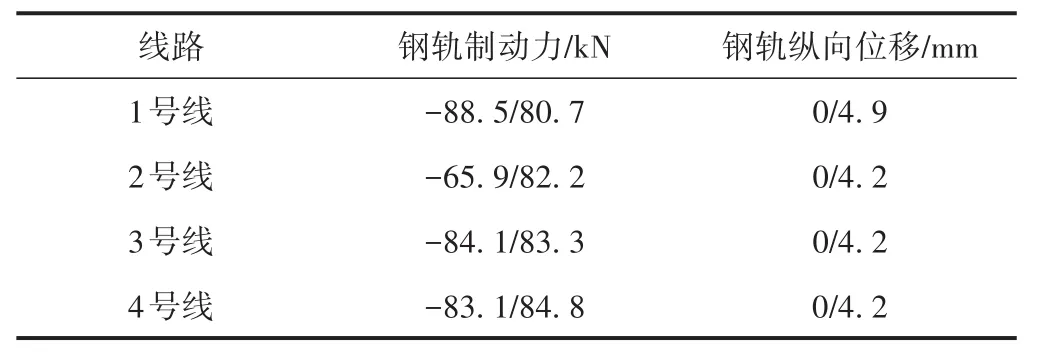
表3 各线钢轨制动力及位移最值

从图9及表3可以看出，钢轨制动力最大幅值出现在右侧连续梁与简支梁连接处；1号线在300 m处（制动荷载加载起点）钢轨制动力出现突变；由于制动荷载加载终点与连续梁端部重合，所以此处出现制动力最大幅值；钢轨纵向位移在两侧路基段为0，纵向位移随着离路基段距离的增加而增大，在连续梁处钢轨纵向位移出现最大值；在制动荷载加载的400 m范围内，1号线钢轨纵向位移比其他3条线大；各条线路的制动力最大幅值差距较小；1号线相比其余各线的钢轨纵向位移最大幅值增大16.7%。

5 结论

本文基于有限元法，以一座预应力混凝土斜拉桥为例，建立了4线预应力混凝土斜拉桥空间耦合有限元模型，分析了温度荷载、列车荷载、制动荷载对无缝线路纵向附加力及变形的影响，得出以下结论：

1）当桥塔升温时钢轨伸缩力、钢轨纵向位移、桥梁纵向位移均无显著变化，因为桥塔升温变形对桥梁和钢轨变形影响不大，钢轨的伸缩力主要是由梁体温度变形引起；桥梁与桥塔同时升温时，钢轨伸缩力最大幅值出现在连续梁端部，并在简支梁梁缝处出现峰值；在连续梁中部一定范围内梁轨相对位移为0，这一范围内钢轨伸缩力几乎没有变化。

2）钢轨挠曲力和钢轨纵向位移随着距加载线路距离的增大而逐渐减小；钢轨挠曲力最大幅值出现在连续梁端部；由于加载位置的不对称，钢轨挠曲力与钢轨纵向位移呈不对称分布。

3）钢轨制动力最大幅值出现在连续梁端部，并在制动荷载加载的起点与终点出现峰值突变；钢轨纵向位移在所加载的1号线400 m范围内出现最大幅值；加载的起点或终点与连续梁端部重合时为最不利位置。