变壁厚半球谐振子设计及参数优化

胡 强，滕 霖，岳亚洲，曹诗音，朱良健，孟 冰

（中国航空工业集团公司西安飞行自动控制研究所，西安 710065）

半球谐振陀螺是利用科氏效应敏感角运动的一种新型壳体振动陀螺[1,2]。相比基于Sagnac 效应的激光陀螺和光纤陀螺，尺寸对半球谐振陀螺的理论精度影响较小，使半球谐振陀螺能够实现相对小体积下的高精度[3]。半球谐振陀螺采用高品质因数的半球谐振子和较为简单的结构，具备精度高、体积小、重量轻、功耗低、可靠性高和环境适应性好等优势，在航空、航天、航海以及陆用等各个领域具有广阔的应用前景[4,5]。

传统半球谐振陀螺采用球面电极与谐振子形成驱动和检测电容，零部件制造和装配难度大、成本高；而新型半球谐振陀螺采用平板电极结构，简化了电极制造以及谐振子、电极的装配问题，但由于该陀螺方案仅利用了谐振子的唇沿面积，与平板电极形成的电容面积大幅降低。为增大电容面积，本文设计了一种变壁厚半球谐振子，通过有限元分析软件ANSYS 对该结构进行了模态分析，并研究了壁厚、内外表面球心距离、内圆角、锚柱中部半径等参数对该结构各阶振型及相应频率的影响。

1 新型半球谐振陀螺和变壁厚半球谐振子

传统半球谐振陀螺采用的“三件套”基本结构如图1 所示，从上到下分别为激励罩、半球谐振子和敏感基座，所用基材均为高纯熔融石英玻璃[6]。图中，激励罩球面内壁上分布有离散激励电极与环形激励电极；敏感基座表面分布有球面的信号检测电极；半球谐振子内、外表面镀制金属薄膜，分别与球面检测电极、球面激励电极形成激励电容和检测电容。为了在半球谐振子表面与球面电极之间形成各向同性的球壳形微小间隙，必须使半球谐振子分别与球面检测电极、球面激励电极完全匹配。这对电极的制造以及谐振子与两个电极的装配提出极高的要求。

图1 传统三件套半球谐振陀螺基本结构[6]Fig.1 The structure of classical three-piece HRG

半球谐振子以四波腹振型振动时，谐振子唇沿处任一质点的运动不仅包含唇沿面内径向振动分量，还包含半球谐振子轴向振动分量。所以，可利用上述轴向振动，将激励电极和检测电极放置在平面内，与谐振子唇沿面产生静电力，实现四波腹振型的激励和检测，如图2 所示。这种新型半球谐振陀螺的激励和检测电极均集成在平板电极上，是一种“两件套”结构[7]。该方案相对采用球面电极的传统半球谐振陀螺方案，将半球谐振子和电极的装配由三维问题转变为二维平面问题，显著降低了制造和装配难度，更有助于减少零件数量和降低陀螺重量。

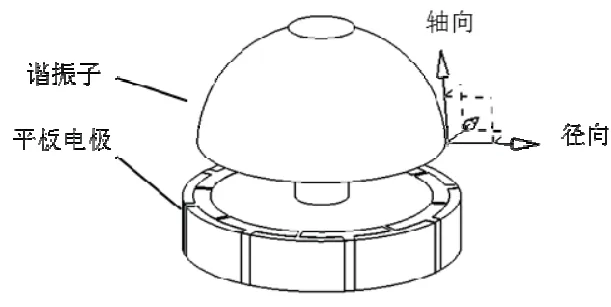
图2 采用平板电极的两件套半球谐振陀螺结构[7]Fig.2 The Structure of two-piece HRG with flat electrodes

新型陀螺方案仅利用了半球谐振子的唇沿底面，由于半球谐振子球壳壁厚通常为毫米级，所以半球谐振子唇沿与平板电极形成的电容面积大幅降低；并且半球谐振子轴向振动幅度仅为唇沿面内径向振动幅度的一半，这将影响谐振子的驱动效率和检测信号大小。为了保持检测电容和驱动电容基本不变，一方面，减小半球谐振子唇沿与平板电极的间隙；另一方面，增加半球谐振子唇沿面积。

对于传统的等壁厚半球谐振子，增加唇沿面积须增加球壳壁厚，导致刚度增大、工作振型谐振频率显著增大，影响半球谐振子性能。为了在增加谐振子唇沿面积的同时抑制谐振频率增大，通过将等壁厚谐振子的内外表面球心离心，可得到一种顶部较薄、唇沿处较厚的均匀变壁厚谐振子结构，如图3 所示。由于该结构内外表面均为球面，因此易于加工。变壁厚结构在增加谐振子唇沿面积的同时也增加了四波腹振型的模态质量，提高了材料利用率，有利于提高陀螺性能。

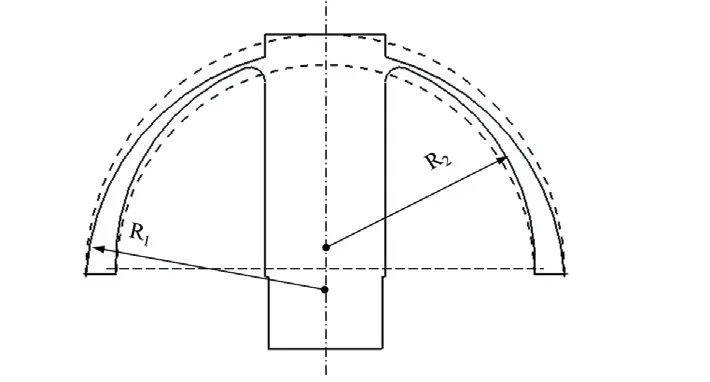
图3 均匀变壁厚谐振子的基本结构Fig.3 The structure of resonator with gradually variable thickness shell

2 变壁厚半球谐振子设计及模态分析

2.1 模态分析的基本理论

对谐振子进行模态分析可得到其本征振型及相应频率[8,9]，这在数学上归结为求系统矩阵的特征值与特征向量的问题。将半球谐振子看作无阻尼多自由度线性振动系统，其自由振动微分方程可表示为：

其中，x是位移列阵；M与K分别为系统的质量与刚度矩阵，均为n×n阶实对称矩阵。可设式(1)的解为：

其中，X为振幅列阵，ω为圆频率，φ为初相位。将式(2)代人式(1)，可得：

式(3)的特征方程为：

通过求解式(4)可得到半球谐振子的固有频率，将固有频率代入式(3)则可解得半球谐振子在各频率下的本征振型。

2.2 传统等壁厚半球谐振子与模态分析

采用有限元分析软件ANSYS 建立某型等壁厚半球谐振子模型并对其进行模态仿真分析，传统等壁厚半球谐振子结构如图4 所示，尺寸单位为毫米。材料选取熔融石英玻璃，在25 °C时，其密度为2.201 g/cm3，杨氏模量为72.7 GPa，泊松比为0.16。

图4 传统等壁厚半球谐振子结构Fig.4 Classical resonator with constant thickness shell

模态仿真分析时，在锚柱底部添加固定约束。仿真得到的谐振子前四阶振型如图5 所示。

图5 等壁厚谐振子前4 阶振型Fig.5 The first 4 modes of resonator with constant thickness shell

图5(a)-(d)分别对应谐振子的二阶弯曲振型、轴挠性振型、一阶弯曲振型与轴弯曲振型，其中二阶弯曲振型为半球谐振陀螺的工作振型，该振型也称为四波腹振型。各阶振型对应的谐振频率如表1 所示，工作振型与相邻振型频差较大，满足半球陀螺的工作要求，但其壁厚仅为0.8 mm，导致唇沿面积较小，影响工作振型激励效率和检测信噪比。

表1 等壁厚半球谐振子各阶频率及对应振型Tab.1 The frequencies and corresponding modes of resonator with constant thickness shell

2.3 变壁厚半球谐振子结构设计与模态分析

为了提高谐振子唇沿面积的同时抑制工作振型谐振频率的增大，本文设计了一种变壁厚谐振子结构，优化后参数如图6 所示。图6 中各参数单位为mm。该结构是通过将谐振子内外球心离心得到的上薄下厚的变壁厚谐振子。

图6 变壁厚半球谐振子Fig.6 The resonator with gradually variable thickness shell

该变壁厚谐振子前四阶振型如图7 所示，图7(a)-(d)分别对应谐振子的轴挠性振型、一阶弯曲振型、二阶弯曲振型与轴弯曲振型。各阶振型对应的谐振频率如表2所示。

图7 变壁厚谐振子前4 阶振型Fig.7 The first 4 modes of resonator with gradually variable thickness shell

对比等壁厚谐振子与变壁厚谐振子结构可以看出，变壁厚结构在基本不改变工作振型谐振频率的基础上，可将谐振子唇沿底部宽度从0.8 mm 增大至1.3 mm，使唇沿面积增大了约65%，有效提高了谐振子的工作面积。

表2 变壁厚半球谐振子各阶频率及对应振型Tab.2 Frequency and corresponding mode of resonator with gradually variable thickness shell

3 结构参数对变壁厚半球谐振子的影响规律

为了研究结构参数变化对变壁厚谐振子前四阶振型谐振频率的影响，通过ANSYS 对不同参数下的变壁厚谐振子进行了模态仿真，所用材料及仿真设置与2.4节一致。选取的结构参数变量如图8 所示，其中a为外表面半径、b为内外表面球心距离、c为内圆角、d为锚柱中部半径。图8 中各参量单位为mm。

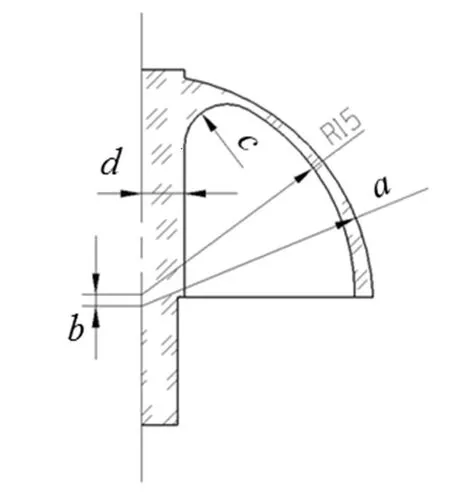
图8 谐振子结构参数变量示意图Fig.8 Schematic diagram of structural parameter variables of resonator

变壁厚谐振子外表面半径对振型谐振频率的影响规律如图9 所示。随着谐振子外表面半径的增大，谐振子壁厚增大，一阶弯曲、轴弯曲与轴挠性振型的谐振频率线性下降，二阶弯曲振型的谐振频率线性增大。其中二阶弯曲振型的谐振频率随壁厚的变化最为显著。因此，谐振子壁厚变化同时显著影响二阶弯曲振型谐振频率及相邻振型间的频差，是谐振子设计的关键参数。

固定谐振子内表面球心，变壁厚谐振子内外球心距离对振型谐振频率的影响规律如图10 所示。随着内外球心距离的增大，谐振子的顶部变薄而唇沿变厚。一阶弯曲和二阶弯曲振型的谐振频率线性下降，轴挠性和轴弯曲振型的谐振频率线性增大。其中，二阶弯曲振型谐振频率变化最显著，轴弯曲、轴挠性和一阶弯曲振型谐振频率变化较小。因此，改变内外球心距离是调节二阶弯曲振型的谐振频率的有效手段。

图9 外表面半径对谐振频率的影响Fig.9 The influence of the outer surface radius on the resonance frequency

图10 内外表面球心距离对谐振频率的影响Fig.10 The influence of the distance between the center of the inner and outer surfaces on the resonance frequency

变壁厚谐振子内圆角半径对振型谐振频率的影响规律如图11 所示。随着内圆角半径的增大，一阶弯曲与轴弯曲振型的谐振频率均线性增大，二阶弯曲与轴挠性振型的谐振频率变化较小。因此，通过调节内圆角半径，可改变二阶弯曲振动与相邻振型间的频差，从而对振型间串扰进行抑制。

图11 内圆角半径对谐振频率的影响Fig.11 The influence of fillet radius on resonance frequency

变壁厚谐振子锚柱中部半径对振型谐振频率的影响规律如图12 所示。随着锚柱中部半径的增大，一阶弯曲、轴弯曲与轴挠性振型的谐振频率均线性增大，而二阶弯曲振型的频率变化较小。因此，改变锚柱中部半径也可调节二阶弯曲振动与相邻振型间的频差从而抑制振型间串扰，且比调节内圆角半径的效率更高。

图12 锚柱中部半径对谐振频率的影响Fig.12 The influence of the radius of the anchor column on the resonance frequency

综上所述，谐振子壁厚及内外表面离心程度对二阶弯曲振型谐振频率影响显著，谐振子内圆角半径与锚柱中部半径对二阶弯曲振型谐振频率的影响较小但对相邻振型频差影响较大。可通过改变壁厚及离心程度调整谐振子的工作振型谐振频率。改变内圆角半径与锚柱中部半径均可增大工作振型与相邻振型间的频率差，但锚柱中部半径对振型间频差的影响更为显著。另外，调节不同参数时，谐振子振型谐振频率的变化率存在差异，所以可进一步对各个关键参数的误差进行分析。

4 变壁厚谐振子工作振型谐振频率测试

为验证表2 中谐振频率仿真结果的准确性，按照图6 所示的结构设计参数加工变壁厚谐振子；针对3 个完成加工的谐振子，开展工作振型（二阶弯曲振型）的谐振频率实验测试。采用敲击法激励谐振子产生振动，同时用激光多普勒测振仪对谐振子谐振频率进行测试，测试实验如图13 所示。

变壁厚谐振子工作振型谐振频率测试与仿真结果如表3 所示。可以看出，工作振型谐振频率测试与仿真结果非常接近，相对误差小于3%，证明本文有限元仿真和分析较为准确。

表3 变壁厚半球谐振子谐振频率测试结果与仿真结果Tab.3 Resonance frequency experimental results and simulation results of resonator with gradually variable thickness shell

5 结 论

采用有限元软件进行半球谐振子模态分析，相比等壁厚半球谐振子，变壁厚半球谐振子在保证工作振型谐振频率基本不变且相邻振型频差较大的情况下，有效增加了唇沿面积；研究了结构参数对变壁厚半球谐振子的影响规律，即通过调节变壁厚谐振子的壁厚与内外表面球心的距离可调整谐振子的工作频率，增大内圆角半径与锚柱中部半径尺寸可增大一阶弯曲振型与二阶弯曲振型的频率差进而减少模式间串扰的发生。设计了一种变壁厚半球谐振子，并对优化后的变壁厚谐振子进行了模态实验，验证了仿真模型的可靠性与准确性。结果表明该结构在保证工作振型谐振频率特性基本不变的前提下，可将谐振子唇沿底部宽度增大至1.3 mm，使唇沿面积相比传统等壁厚半球谐振子增大了约65%，有效提高了激励电容和检测电容面积。最后对3 个变壁厚谐振子工作振型的谐振频率进行了实验测试，测试与仿真结果非常接近，相对误差小于3%，证明本文有限元仿真和分析较为准确。