基于改进人工势场的无人地面车辆路径规避算法

刘冰雁，叶雄兵，王新波，贾 珺，王 涛

(1. 军事科学院，北京100091；2. 解放军32032 部队，北京100094)

无人地面车辆(UGV)，最初仅作为爆炸物清除设备，随着城市化发展，如今已能够担当运输、护送等多类型使命。然而，城市环境最大的特点是高楼林立，而无人地面车辆应用的最大难点则是规避路径的自主规划。国内外关于路径规划研究与实现的基本方法依据对周围环境信息的掌控情况[1-4]，可大致可归纳为：全局路径规划方法和局部路径规划方法。全局路径规划，是指对全局环境信息完全已知，不需要进行环境的实时更新，根据已知信息建立合适的环境模型，再据此规划出合适路径的方法。典型的全局规划法有：可视图法、栅格法、自由空间法等，其中A*[5,6]、Dijkstra[7]算法最为常用。全局路径规划，由于事前已知环境信息不再需要大量采集周围环境信息，能够减少计算量，但其规划效果却与环境粒度划分密切相关。局部路径规划，是一种在线规划法，是指移动体不完全了解周围环境，实时采集周围环境信息，动态更新路径的方法。典型的局部规划法有：人工势场法，遗传算法[8]、蚁群算法、粒子群算法[9]和模糊逻辑算法等[10]。局部路径规划，是在环境信息完全未知或部分未知情况下进行，具有实时性强，响应速度快等优点。

人工势场法(Artificial Potential Field, APF)，是局部路径规划法中的一种[11,12]，与其它局部路径规划法算法的特性比较如表1 所示。相比较，人工势场法具有数学描述清晰、运算迅速、计算量小、硬件要求低以及规划路径平滑等优势[13]，目前在无人机、无人车、仿生人等的路径规划研究中应用广泛。例如，文献[14][15]针对无人机航路规划问题，借鉴人工势场思想，提出了能够满足任务执行指标并保障飞行安全的路径规划方法。文献[16][17]针对移动不够灵活、易入“陷阱”的机器人路径规划问题，发挥人工势场法便于控制、路径平滑的优势，提出了路程短、效率高的路径规划方法。

但是，人工势场法也存在局部极小值和震荡等不足，使得人工势场法不适合直接用于城市环境规避路径自主规划问题。为进一步解决无人地面车辆(UGV)在城市自主规避难的问题，通过构建城市环境人工势场模型，剖析经典人工势场模型运用于城市环境的优势与不足，改进人工势场函数、调整势场作用区域，构建以远距点斥力忽略、障碍点引力减弱的综合势场模型，提出了一种基于改进人工势场的城市障碍规避算法。

表1 局部路径规划方法比较Tab.1 Comparison of local path planning methods

1 城市规避人工势场模型

由Khatib 提出并被称为人工势场法的一种虚拟力场法，是运用空间势场力来研究物体所处的相对运动，并通过不断变化的位置势场来控制物体的规避运动，其势场变化及路径规划效果如图1 所示。人工势场法基本思路是：通过目标位置的引力势场和障碍物的斥力势场共同作用，搜索出一条无碰撞的最优路径。人工势场法相较于其他规避方法具有数学描述简单、运算量小、实用性高以及路径平滑的比较优势。

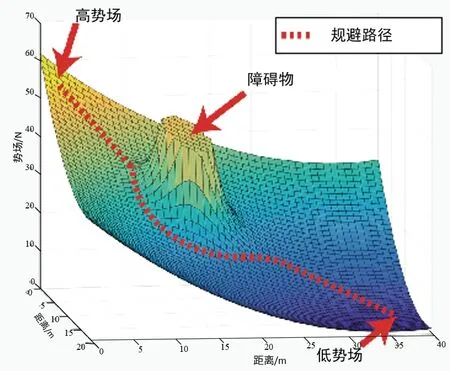
图1 人工势场规避路径示意图Fig.1 Schematic diagram of artificial potential field avoidance path

城市规避人工势场中，目标位置将对无人地面车辆产生引力势场，城市建筑对无人地面车辆产生斥力势场，其受力情况如图2 所示。引力势场与斥力势场的合力场将决定无人地面车辆的机动方向和机动速率。

图2 无人地面车辆在人工势场中的受力示意图Fig.2 Diagram of force exerted on unmanned ground vehicle in artificial potential field

于是，无人地面车辆在城市任意位置的综合势场可表述为：

式中：x是无人地面车辆当前位置状态矢量；U（x）是无人地面车辆所受的综合势场；Uatt（x）是目标位置对无人地面车辆的引力势场；Urep（x）是城市障碍对无人地面车辆产生的斥力势场。

图3 城市环境中的人工引力势场与斥力势场Fig.3 Artificial gravitational potential field and repulsion potential field in urban environment

如图3 所示，目标位置对无人地面车辆产生的引力势场大小与两者之间的距离大小相关，两者间的距离越大势能则越大，反之则越小。因此，引力势场与两者之间的距离成正比，引力势场可表述为：

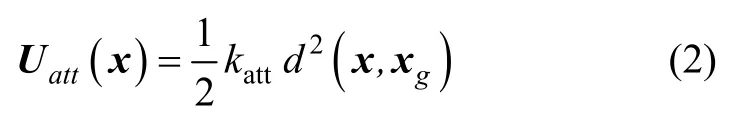
式中：katt是引力势场增益系数；x是无人地面车辆的当前位置矢量；xg是目标位置矢量；d2（⋅）是欧氏距离计算函数。

由该引力势场对无人地面车辆所产生的引力，为引力势能的负梯度：

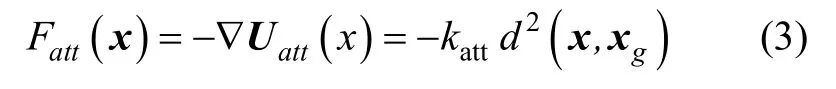
与此同时，城市障碍将对无人地面车辆产生斥力势场。斥力势场的大小由无人地面车辆与障碍之间的空间距离确定，两者之间的距离越小斥力势场越大，反之越小。由此，斥力势场可表述为：

式中：krep是斥力势场增益系数；xo是城市障碍的位置矢量；dn是无斥力区域范围。

由斥力势场所产生的斥力，为斥力势能的负梯度：

2 人工势场优劣分析

人工势场法，能够很好地将空间规避行为用数学表达式进行描述，为规避路径规划方法提供了具体化的、有效的解决方案，具有显著优点：

①实时规避性

相较于其他路径规划方法，人工势场法具有很好的实时规避性能，能够将路径规划建模的重心聚焦于无人地面车辆飞行方向以及城市障碍，只需要较少的运算就能达到较好的实时规避效果[18-20]。

②路径平滑

无人地面车辆在规避城市障碍过程中，人工势场法能够随着周围空间环境采集无人地面车辆与城市障碍的状态信息，并在双方之间的斥力势场与引力势场中体现。人工势场法在路径规划中，只需根据当前位置结合综合势场即可获得平滑而安全的路径，不需像别的算法那样还要进行路径平滑、避障检测等操作，应用优势明显。

然而金无足赤，传统人工势场法在大量现实应用中也暴露了自身结构性的缺陷，即存在局部最优解。所谓局部最优解是指引力势场与斥力势场等效反向作用，致使无人地面车辆原地驻留或者来回震荡，无法继续向目标位置行进。局部最优解主要有两方面的体现：

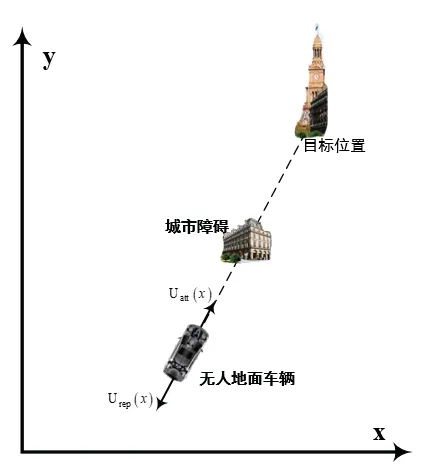
图4 目标不可达现象示意图Fig.4 Target unreachable phenomenon diagram

① 目标不可达

无人地面车辆在规避城市障碍的过程中，如果此刻城市障碍位于目标位置附近，当无人地面车辆离目标位置以及城市障碍都较远时，受到的引力势场较大，而斥力势场较小，斥力势场小于引力势场，这时无人地面车辆将在合力势场作用下向着目标位置行进；然而，无人地面车辆距目标位置和城市障碍越来越近，所受引力势场越来越小，而斥力势场反而越来越大，当引力势场与斥力势场等大反向时，这将可能致使无人地面车辆在当前位置震荡或驻留，无法到达目标位置，其情况如图4 所示。

② 局部极小陷阱

当无人地面车辆临近城市障碍时，如果目标位置正好在城市障碍另一端，此时无人地面车辆所受到的引力势场与斥力势场之间角度为180 °且大小相等，无人地面车辆将停留在此处合力为零的点，即局部极小陷阱，最终无法成功到达目标位置，其情况如图5 所示。本文将局部极小陷阱分为两类：

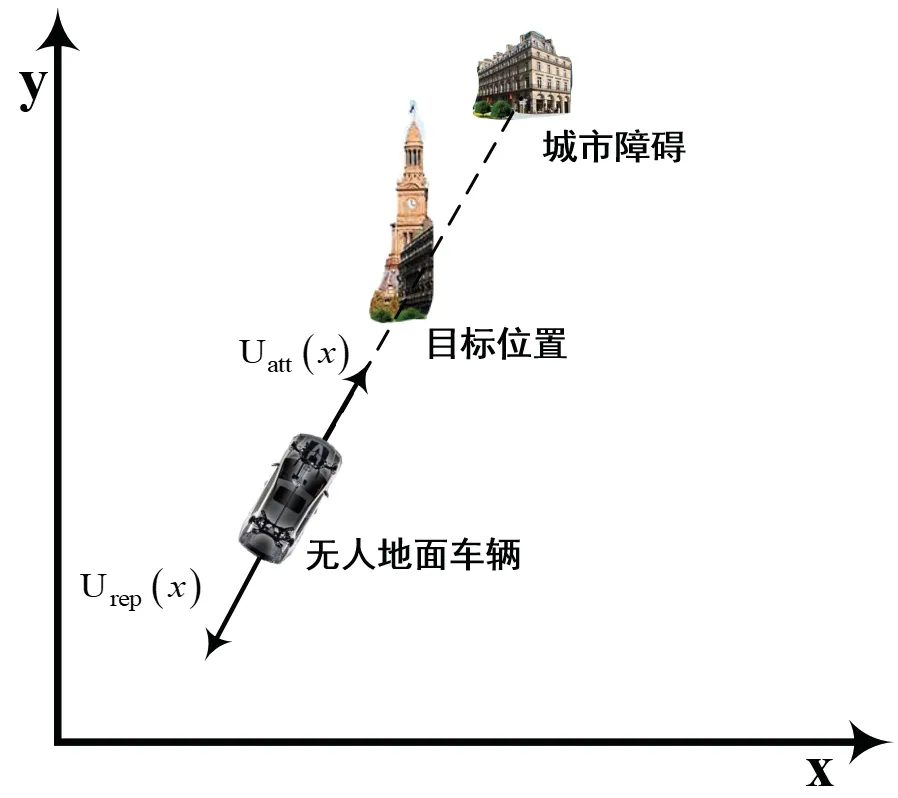
图5 局部极小陷阱示意图Fig.5 Local minimum trap schematic

I 局部极小值问题

第一类局部极小陷阱是势场遇到局部极小值问题，处于该陷阱时任意方向均为极小值，其综合势场呈凹状。局部极小值可根据定理4.1 进行判定。

定理4.1[21]设U（x）为Rn→R的一个二阶连续可微函数，g∈Rn是U（x）的驻点。若在g处的Hessian 矩阵正定，则g为局部极小值点；反之g则不一定为极值。

II 鞍点问题

第二类局部极小陷阱是鞍点问题，即在某个或某些方向上的综合势场均为局部最小值。当无人地面车辆沿着这些局部最小值的方向机动时，可能因为势场不足而在鞍点附近往复徘徊无法继续行进。

设以角度φ∈ ［ 0,2π）为参数的方向矢量为：

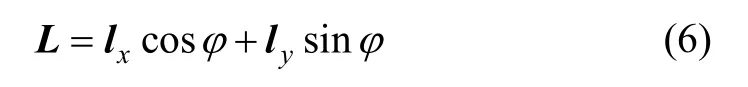
式中：lx与ly是运动方向的单位矢量。

求解矢量lx与矢量ly的一阶和二阶偏导数并满足式(7)的所有空间位置以及对应的角度参数φ，即可得到第二类陷阱中的鞍点位置及方向。

3 综合势场改进模型

人工势场法通常是将终点作为引力源，障碍作为斥力源，引力势场与斥力势场在空间合成综合势场，驱使运动体沿着势场减弱方向在规避障碍的同时到达终点。

在无人地面车辆规避机动的运用中，在距城市障碍较远时应该弱化斥力势场，以免出现过早轨迹偏离现象。同时，在抵近城市障碍时应弱化引力势场，以免出现局部震荡现象。如图6 所示，本文构建了以远距点斥力忽略、障碍点引力减弱的综合势场模型：

式中：U（x,Δs）为当前位置x无人地面车辆所受的综合势场；Uatt（x）为引力势场；katt为引力势场系数；Urep（x）为斥力势场；krep为斥力势场系数。

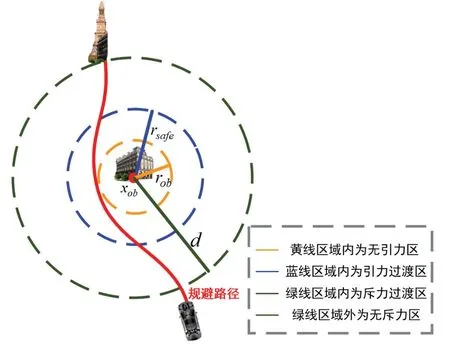
图6 无人地面车辆规避机动人工势场示意Fig.6 Unmanned ground vehicle evading maneuvering artificial potential field signal

3.1 引力势场模型

为顺利规避城市障碍并避免局部震荡现象，对引力势场函数进行了改进，在城市障碍附近设置弱化引力势场的环形区域：

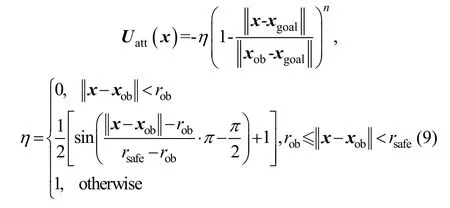
式中：η为与城市障碍距离相关的吸引场系数；xob为城市障碍位置矢量；xgoal为目标位置矢量；n为正整数；rob为城市障碍的威胁范围；rsafe为引力衰减区范围；为2-范数。

3.2 斥力势场模型

为紧跟目标方向避免过早偏离，采用势场平滑过渡策略对斥力势场函数进行改进：

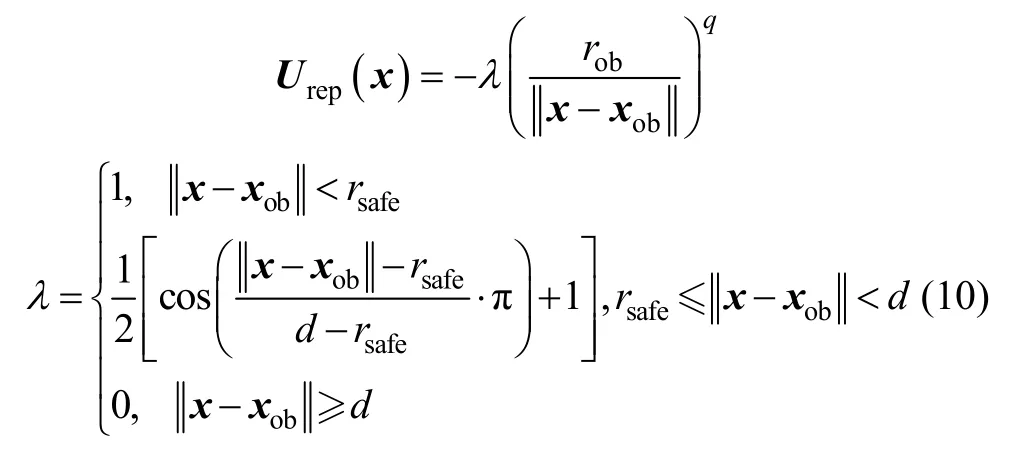
式中：λ为斥力势场系数；q为正整数；d为斥力过渡区作用范围。

3.3 连续可微证明

通常，对人工势场模型进行负梯度求解可得到势场力，但要求综合势场模型是连续可微的。然而，本文所构建势场模型的系数均是由无人地面车辆相对位置所确定，特别是引力势场模型和斥力势场模型系数都是与相对位置相关的分段函数。为了检验通过所构建的势场模型可以得到连续的势场力，本节对各分段函数的连续可微性给予证明。

对于引力势场函数Uatt（x），其连续可微性主要看式(9)中的分段函数η：

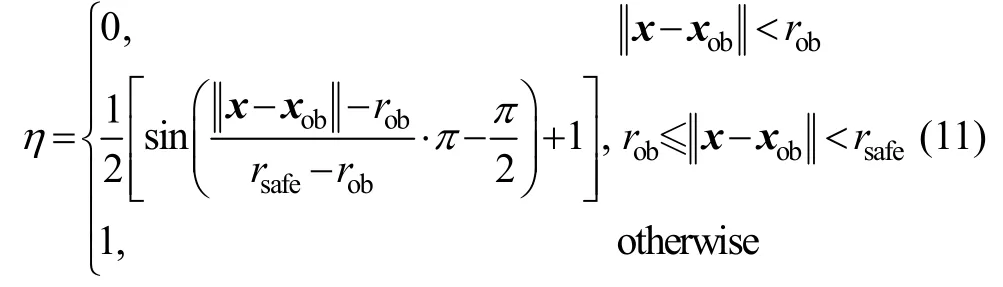
由此，证明分段函数η是连续可微，从而可知引力势场模型Uatt（x）亦是连续可微的。同理，可证明斥力势场模型Urep（x）的连续可微性。

4 算例分析

通过将改进的人工势场法与经典人工势场法以及常用的迪杰斯特拉(Dijkstra)、快速扩展随机树(RRT)路径规划算法进行仿真实验，以对比说明改进算法的应用优势。其中，Dijkstra 算法以起始点为中心向外层层扩展，直到扩展到终点为止，是典型的单源最短路径算法，主要用于计算一个节点到其他所有节点的最短路径；RRT 算法通过对状态空间中的采样点进行碰撞检测，避免了对空间的建模，能够有效地解决高维空间和复杂约束的路径规划问题。针对城市环境规避路径规划问题，运用本文所提方法进行仿真，以检验本文所提算法的有效性。

4.1 算法对比

为说明改进人工势场法的比较优势，分别与经典人工势场法以及常用的最短路径算法进行了仿真对比。如图7 所示，设有一屏障规避问题，即需自主规划出从绿色点出发顺利绕过两屏障到达蓝色叉地的最短路径，在1.6 GHz、1.8 GHz 双核CPU、8 GRAM 计算硬件上，运用相同的PyCharm 工具，分别运用四种算法进行求解。

运用典型广度优先搜索法（Dijkstra 算法[22-24]）可得到如图7(a)所示的红色路径。在Dijkstra 算法求解过程中，需预先设定搜索区域（图中黑框部分）并采取以起始点为中心向外层层扩展的方式（图中蓝色叉点代表已搜索节点），使得搜索过多无关节点，平均耗时0.48 s，所得路径棱角明显，路径长度93.3 m。运用增量式、概率完备且不最优的路径规划算法（RRT 算法[25-27]）可得到如图7(b)所示的红色路径。RRT 算法采取以初始状态作为根节点、目标节点作为叶子结点的搜索树方式（图中绿色支路为已搜索区域），平均耗时0.62 s，所得路径曲折，长度111.4 m。运用经典人工势场法可得到如图7(c)所示的红色路径。经仿真发现，接近目标过程中路径会出现波动，当引力势场与斥力势场等大反向且受障碍阻断时，会产生局部震荡（图中红色加粗部分），出现目标不可达现象。运用改进人工势场法，平均耗时0.29 s 后顺利到达目标位置，所得路径如图7(d)所示，路径长度91.1 m，平滑效果更好。总体来说，本文算法比Dijkstra 算法路径规划效率提升了 39.5%，比 RRT 算法路径规划效率提升了53.2%。

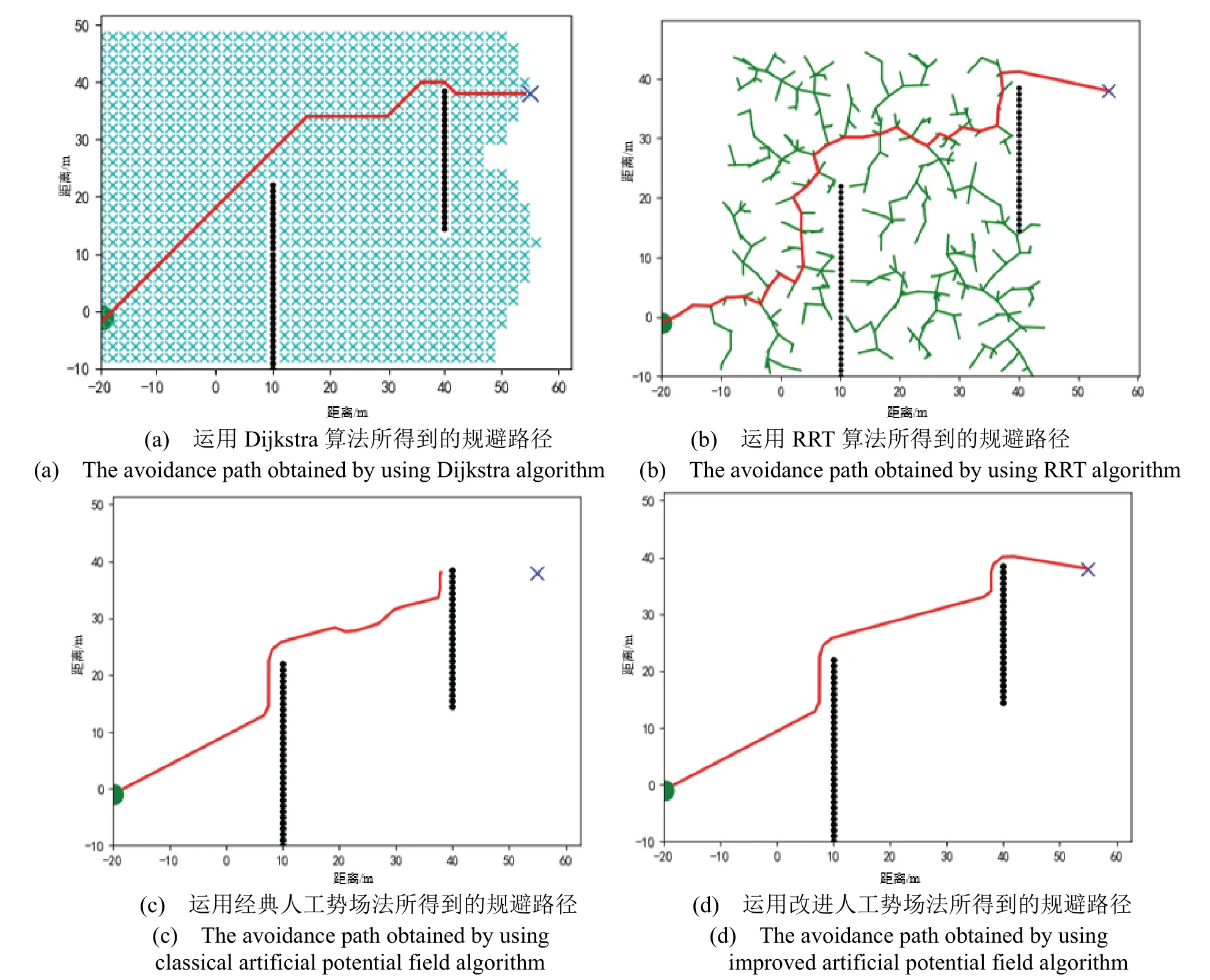
图 7 屏障规避问题的不同算法求解效果Fig.7 Different algorithms to solve the barrier avoidance problem

因此，改进的人工势场法能有效弥补经典人工势场在路径波动、局部震荡以及目标不可达方面的不足，与两种常用路径规划算法相比较耗时短、路程少、路径平滑，具有较强对比优势和应用优势。

4.2 算例求解

设无人地面车辆质量为50 kg，从起始地穿过城市建筑到达目标地域，期间有高楼林立，需要无人地面车辆自主规划出最优规避路径。如图8 所示，设计了三个不同复杂度的城市环境障碍环境，以验证本文算法的有效性。

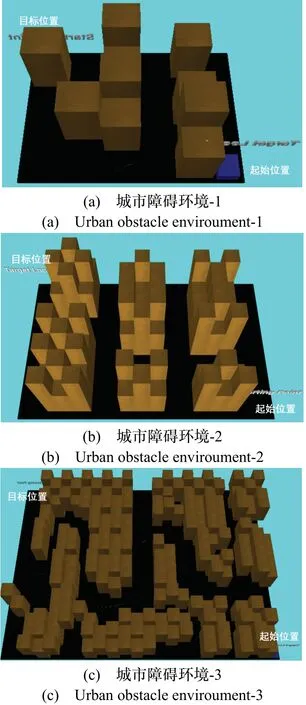
图8 城市障碍环境Fig. 8 Urban barrier environment

在运用基于改进人工势场的城市环境规避算法求解过程中，将模型参数设置为：krefer=0.2，katt=0.4，krep=0.4，δ=0.92，η=0.4，n=1，q= 1，λ=0.4，rsafe= 5m ，d=3m。

如图9 所示，较为详细地展现了无人地面车辆在城市环境-2 中规避建筑的路径生成过程。该方法可以根据当前城市环境实时自主规划最佳的规避路径，最短路径为106 m，并顺利抵达目标位置。

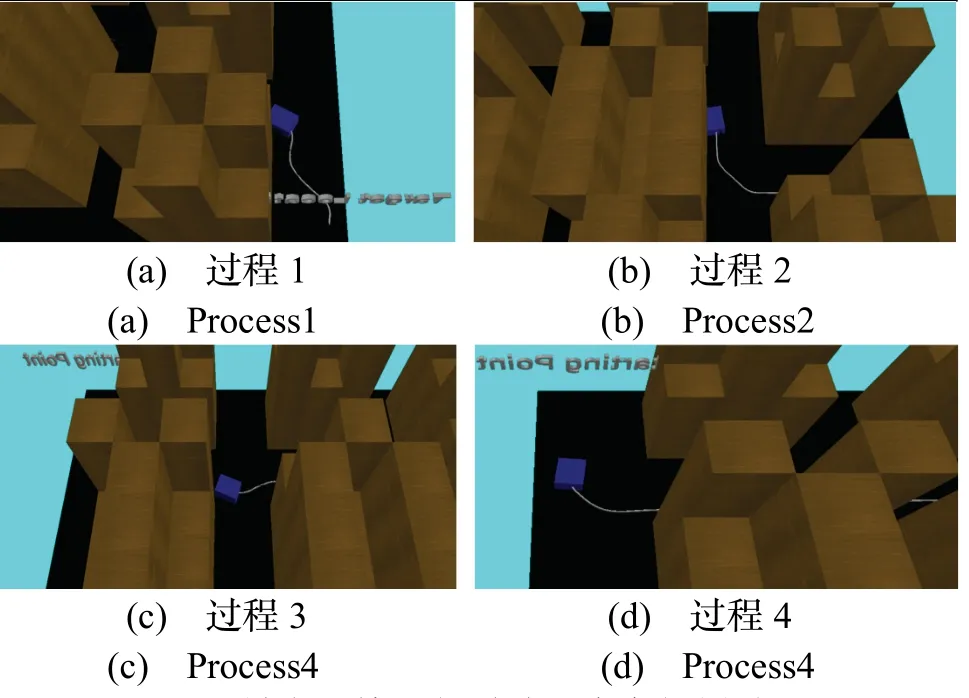
图9 城市环境-2 规避路径自主规划过程Fig.9 The process of autonomous planning of avoidance path for urban environment-2

如图10 所示，展示了3 种不同城市环境复杂度下规划得到的最佳规避路径，各条路径均能根据目标位置，结合当前城市环境，自主规划出最合适的路径，均能顺利到达目标位置，满足城市环境中障碍自主规避的需求。

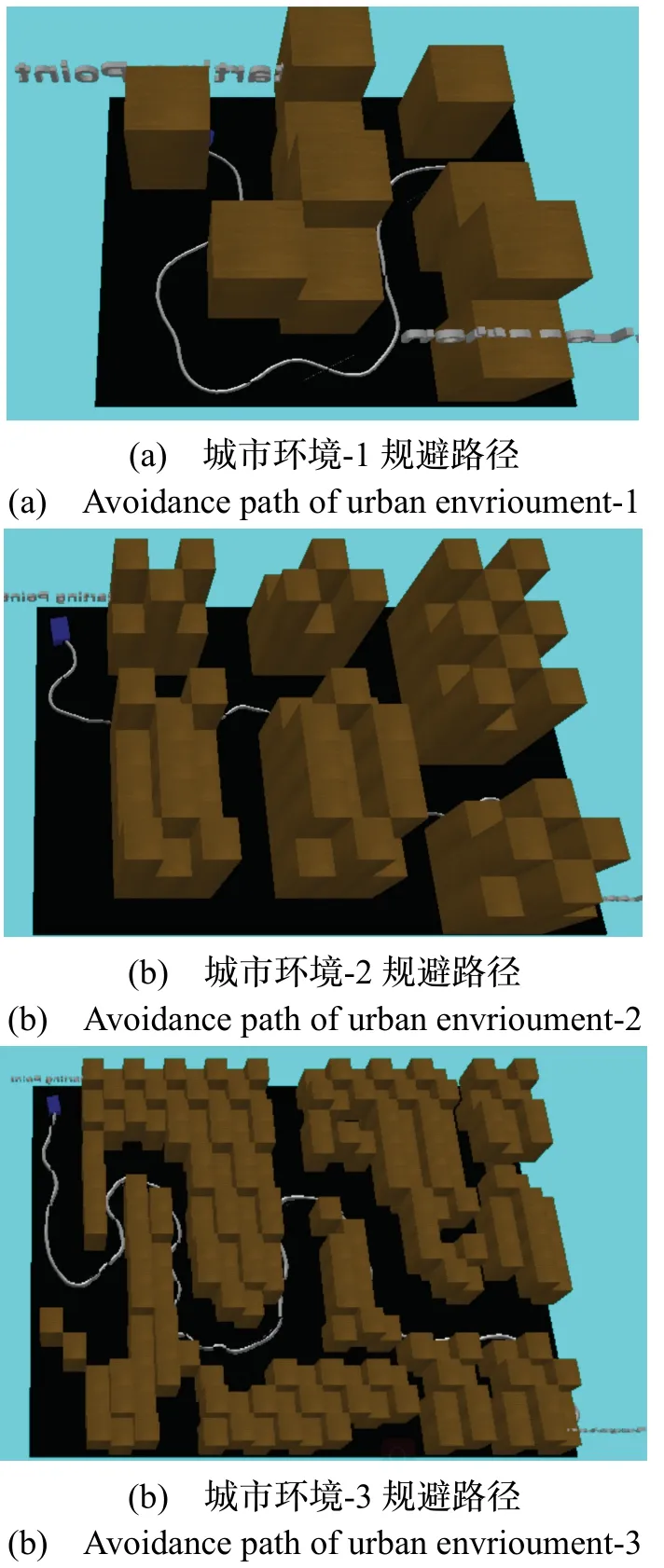
图10 城市环境规避路径Fig.10 Urban environment avoidance path

此外，为了检验算法对城市动态障碍的规避性能，在仿真场景中增添了动态障碍物，即在无人地面车辆行进过程中突遇一黄色障碍车辆的逼近。

如图11 所示，为最初无人地面车辆在城市环境中的最优机动路径。但当无人地面车辆行进过程中，突然临时出现一黄色障碍辆车，且其行进路线与无人地面车辆路线冲突。为了避免两车相撞，无人地面车辆依据本文算法临时动态规划了新的路径。

图11 无人地面车辆在城市环境中的最佳机动路径Fig.11 Optimal mobility path of unmanned ground vehicle in urban environment

根据本文算法，当障碍车辆驶进人工势场的斥力过渡区（d=10m）后，如图12 所示无人地面车辆自动改变了机动方向并采取了动态规避行为。

图12 无人地面车辆改变机动方向规避障碍车辆Fig. 12 The unmanned ground vehicle changes its maneuvering direction to avoid the obstacle vehicle

当无人地面车辆顺利规避动态运动的障碍车辆且距离大于无引力区（rob=5m）后，如图13 所示无人地面车辆将主要受引力场引导继续向目标位置驶去。

图13 无人地面车辆成功规避障碍车辆Fig.13 The unmanned ground vehicle successfully evaded the obstacle vehicle

当障碍车辆驶离人工势场的斥力过渡区（d=10m），如图14 所示无人地面车辆仅受引力势场作用，将实现与最初路径相一致的行驶方向。

图14 无人地面车辆继续向着目标位置驶去Fig.14 The unmanned ground vehicle continued to move toward the target position

面对动态运动的障碍车辆，运用本文算法，无人地面车辆动态规划的最优机动路径如图15 所示。整个规避过程实现了对障碍车辆的动态规划，并能在规避过后尽快向目标位置继续行进。整个路径平滑、路程少、应变能力强，将有助于更好地解决城市复杂环境自主规避问题。

图15 无人地面车辆的整个动态规避路径Fig.15 The entire dynamic avoidance path of the unmanned ground vehicle

5 结 论

城市化，是未来社会建设与发展的重要阶段性标志。为进一步解决无人地面车辆(UGV)在城市环境自主规避难的问题，提出了一种基于改进人工势场的城市环境规避算法。构建了城市环境人工势场模型，给出了引力势场、斥力势场以及综合势场函数，将空间规避路径规划问题转化为势场力作用问题。深入剖析了经典人工势场模型运用于城市环境的优势与不足，改进了人工势场函数、调整势场作用区域，构建了以远距点斥力忽略、障碍点引力减弱的综合势场模型，避免了传统人工势场法存在过早轨迹偏离以及局部震荡现象，实现了在城市环境中的自主规避。算例分析表明，论文算法具有耗时短、路程少、路径平滑的对比优势，能够更有效地应对城市障碍以及动态车辆规避问题，为复杂环境下规避路径自主规划提供了新思路。同时，对于其他领域中的规避路径规划问题具有较强借鉴意义。