助燃空气对乙烯裂解炉NOx排放的影响

2020-04-06胡贵华叶贞成杜文莉

化工学报 2020年2期

胡贵华，叶贞成，杜文莉

（1 华东理工大学信息学科与工程学院，上海200237； 2 化学工程联合国家重点实验室（华东理工大学），上海200237）

引言

乙烯裂解炉是乙烯生产装置乃至整套石油化工工业的龙头，其生产能力的高低，直接决定了整套乙烯装置的生产规模、产量和产品品质。乙烯裂解炉在燃烧过程中形成的氮氧化物(NOx)是主要大气污染物之一，燃烧产生的NOx中，NO 占95%以上[1]。排入大气的NOx引起酸雨和光化学烟雾污染，破坏臭氧层，严重破坏生态环境，危害人类健康。然而，以往的研究更为关注裂解炉的产品收率与节能问题，对于NOx减排指标关注很少[2-3]。所以，控制乙烯裂解炉的NOx排放对防止环境污染具有积极意义。

裂解炉炉膛内燃料气的燃烧是一个复杂的物理化学过程，涉及一系列的流动、传热和化学反应过程。在乙烯裂解炉燃烧模拟的研究中，目前仍大量使用简单的两步或五步化学反应机理[4-6]，没有考虑燃料的详细化学反应动力学特征，所以，基于简单湍流-化学相互作用模型和宏观反应机理的CFD模拟对NOx的生成预测缺乏可靠性。为了有效解决这一问题，目前国内外的学者通过在燃烧模拟研究中嵌入详细反应机理提高预测可靠性[7-9]。但是，反应个数和组分数随着染料分子链长度的增加呈指数增加，另外，包括大量组分和反应的机理实体通常不仅是非线性耦合的，而且时间尺度不一样。所以，将这些详细反应机理嵌入到CFD 中，计算量将急剧增加，给模拟带来很大的困难[10]。针对这个问题，许多学者尝试采用简化详细的化学反应机理方法对燃烧过程进行研究。Hewson 等[11]采用简化机理研究碳氢化合物与空气非预混燃烧过程NOx的产生及其燃烧机理，其反应历程所包含的步数取决于所需精确描述宏观现象的数目。Stefanidis 等[12]通过对七步到十二步反应的六种预混燃烧的简单机理进行模拟分析后，确定八步简化反应机理能够较为满意地预测炉膛内的温度分布及包括NO 等污染物的形成。Tang等[13]采用两种湍流燃烧模型——涡耗散概念(eddy dissipation concept，EDC)模型和联合概率密度函数(probability density function，PDF)模型与两种简化反应机理(降维和储存/检索)耦合进行有限速率化学计算。但是这些研究基本上都是针对火焰的燃烧动力学所作的理论研究和实验验证，其成果对于预测工业规模裂解炉NOx产生的普遍性指导意义是有限的。

本文采用郑清平等[14]研究的GRI-Mech 3.0简化机理模型，建立了标准Flame D 的数值模型，并使用EDC 燃烧模型与GRI-Mech 3.0 简化机理联合模拟的方法模拟湍流扩散的燃烧过程，仿真结果验证了GRI-Mech 3.0 简化机理预测NO 排放的准确性和EDC-GRI3.0 模型的可靠性。在此基础上，使用CHEMKIN 和CFD 相结合的方法研究了助燃空气对降低裂解炉NO 排放的影响。结果表明：空气预热温度300～600 K 和过量空气系数1.1 被确定为最佳操作范围，为乙烯裂解炉的工业改造和优化提供了理论依据。

1 数学模型

1.1 湍流模型

由于烟气的流动是湍流，炉内发生复杂的燃烧和传热过程，需要求解质量、动量和能量、湍流动能、湍动能的耗散率以及组分输运方程。采用雷诺平均Navier-Stokes (RANS)方程描述三维可压缩湍流流动。Realizablek-ε模型在提高火焰稳定性、反应效率以及降低NOx排放等方面优于其他湍流模型[15]，所以本文选用Realizablek-ε湍流模型封闭方程。得出的输运方程的一般形式可写为

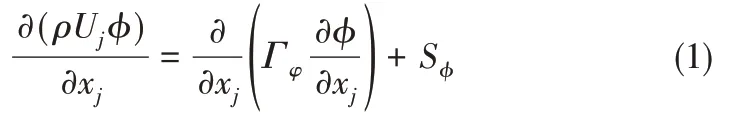
1.2 辐射传热模型

辐射传热模型应用离散坐标模型(discrete ordinates)[16]，其求解有限数量离散立体角发出的辐射传播方程，辐射传播方程的个数与空间坐标系中的方向矢量个数相同，其数学表达式为

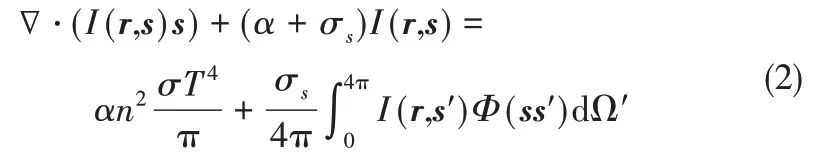
本文采用多灰气加权模型(WSGGM)计算烟气的辐射特性[17]，该模型把真实气体的黑度分为若干灰气黑度的加权和，具有较高的计算精度和效率。

1.3 燃烧反应动力学机理模型

本文研究的乙烯裂解炉中燃烧反应动力学是基于郑清平等[14]研究的GRI-Mech 3.0 简化机理模型，该模型包括24 组分的42 步甲烷燃烧过程，能详细准确地描述裂解炉内的燃烧过程中的化学反应行为且不影响计算精度。

目前几种常用的炉膛燃烧模型中，有限速率模型只适用简单动力学机理[18]，而要在裂解炉的数值仿真引入GRI-Mech 3.0 简化燃烧机理就必须使用EDC 模型，该模型的湍流流动结构适合详细燃烧机理的计算[19]。EDC 模型假定分子混合和随后的反应发生在Kolmogorov 规模的小湍流结构中，在该结构中湍动能被耗散成热量[20]。该模型考虑了湍流结构中详细的燃烧化学反应机理，可以更准确地跟踪化学反应过程，与湍流的相互作用更符合物理意义。EDC模型的复杂的湍流结构导致了FLUENT计算速度很慢，此时可以使用非结构化自适应列表法（ISAT）[21]来提高EDC 模型的运算速度，为保证收敛精度，将ISAT 的误差容错率设置为0.0001。EDC 模型更适用于反应速率较低的化学反应[22]，比如裂解炉燃烧中的NO和CO生成过程。

方程式(1)的组分输运方程中物质i的源项计算公式为

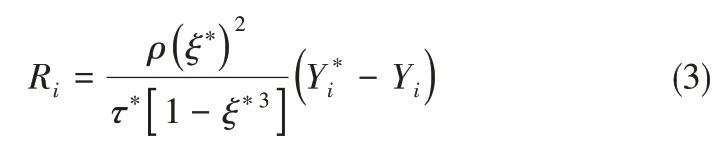
其中，

2 GRI-Mech 3.0简化机理模型验证

2.1 几何结构和操作条件

Sandia Flame D 是一种稳定在一个导向燃烧器上的甲烷-空气射流扩散火焰，其燃烧器结构包括三个部分：中心射流、值班火焰和空气伴流。中心射流是由25%甲烷和75%空气组成的燃料流，中心射流外面紧接着被空气伴流包围的环形值班火焰，作用是点火与稳燃。Sandia Flame D 结构和操作条件分别如图1和表1所示[23]。

2.2 网格划分

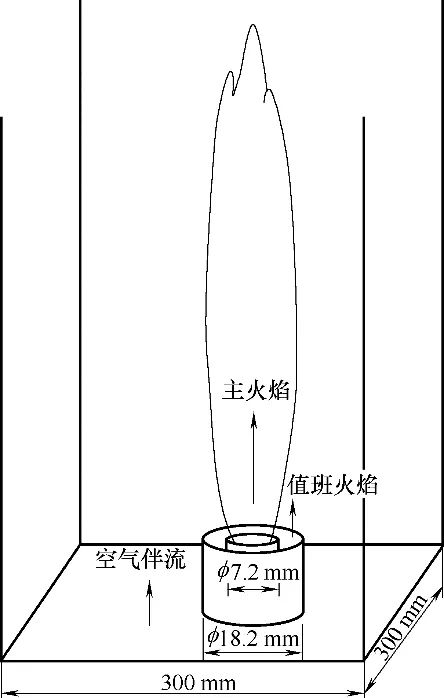
图1 Sandia Flame D燃烧器结构示意图Fig.1 Schematic diagram of Sandia Flame D burner

采用Gambit 软件[24]对Flame D 进行几何建模和划分网格，计算域延伸到射流出口平面的上游，以确保燃料、值班火焰和空气伴流管道内的湍流充分发展。为了保证计算的准确性，对速度梯度较大的部分，如速度出口和对称轴附近网格使用六面体和四面体混合网格做了必要的细化，其余部分采用六面体结构网格，网格总数为189537 个。Flame D 网格模型如图2所示。

2.3 数学模型和模拟方法

采用EDC 燃烧模型结合GRI-Mech 3.0 简化机理联合模拟Flame D 燃烧过程，使用Realizablek-ε湍流模型模拟烟气流动过程，选用DO 模型模拟辐射传热过程。利用Ansys Fluent 14.0[25]对Flame D 的燃烧过程进行模拟计算。

质量、动量、能量、湍流、化学组分和辐射守恒的控制方程用控制体积法连续地求解。非线性控制方程用第二迎风格式隐式离散，线性化产生出每一个计算单元格中的因变量的方程组。然后求解由此产生的一个稀疏系数矩阵的线性系统，产生一个更新的流场方案。采用适合的下松弛因子以防止不稳定的解。因为高的压力校正下松弛值引起不稳定，采用带有轻微更守恒的下松弛值(≤0.7)的压力联立方程的半隐式算法(SIMPLE)。除了能量和辐射方程残差收敛标准为10-6，其他方程的残差收敛标准均为10-3。

表1 Flame D入口速度和组分条件Table 1 Inlet velocity and composition conditions of Sandia Flame D

图2 Flame D模型网格Fig.2 Grid of Flame D model

2.4 结果与分析

图3中给出了Flame D 燃烧的速度与温度云图。由图3(a)可知，当甲烷从中心射流喷嘴以高速射入，与空气伴流射入的空气相混合时，由于气体的扩散性，燃烧火焰的速度呈由喷嘴中心向四周由大到小逐渐减小的趋势，在火焰区外不发生变化。在图3(b)中，由于受到火焰的速度影响，燃烧火焰的温度呈现从中心一点向外逐渐扩散的分布趋势，燃料的充分燃烧造成火焰温度的升高。烟气速度和温度梯度的变化趋势一定程度上反映了火焰的形状，没有出现熄火和燃烧不稳定的状况。

图4 给出了Flame D 轴向和径向温度分布的模拟值和实验数据[26]的比较，轴向和径向长度使用主火焰喷嘴直径d进行了无量纲化。从比较结果来看，该模型模拟的轴向温度分布与实验数据吻合很好，火焰最高温度范围与实际相同，这从一方面说明了采用Realizablek-ε湍流模型与EDC-GRI 3.0耦合模型结合的方法来数值模拟湍流射流火焰是可靠的。从图中还可以看出，在中心轴大约50d处出现温度峰值2000 K。

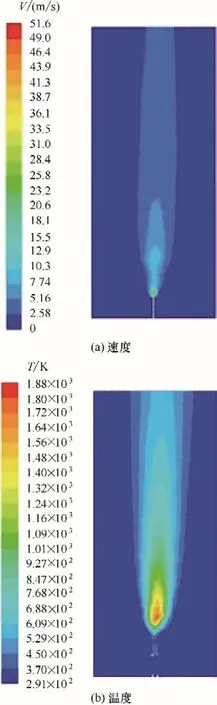
图3 Flame D燃烧速度与温度云图Fig.3 Velocity and temperature contours of Flame D combustion

图5 为Flame D 的O2与CO2质量浓度轴向分布云图。从图中可看出，燃烧反应物O2的浓度随着反应区域的增大及燃烧的充分程度的增加而减少，而燃烧生成物CO2的浓度则相应地增加。一般来说以往采用简化化学反应机理对Flame D 模型进行数值仿真时，只是满足了工程上的热需求，这将导致其仿真结果对燃烧反应后的化学组分的浓度场的预测效果很差而分布云图会严重失真。然而，本文采用EDC-GRI 3.0 反应机理模型对Flame D 进行数值模拟，其结果很直观地表现出各组分的浓度分布，成功克服了以上弊端。同时从O2轴向剖面可以很清晰地观察到不同火焰段的空气夹带与燃烧火焰的厚度，这也表明了仿真过程并未出现甲烷射流火焰常见的局部熄火问题，证明了EDC-GRI 3.0 耦合模型在燃烧过程的适用性。

图4 Flame D温度分布模拟值与实验数据比较Fig.4 Comparison of temperature distributions with simulation results and experimental data for Flame D

图6（a）为NO 质量分数的分布云图，图6（b）显示了模拟的NO 沿中轴线方向上的分布与实验数据的比较。由图可知，NO 的浓度随着燃烧充分程度变化而先增大后减小，大约58d处出现最大值。在峰值以前，火焰温度较低，主要产生快速型NO，在50d处燃烧温度出现最大值，此处火焰温度较高造成大量的热力型NO 累积，在随后几米出现浓度峰值，此后由于氧的不足造成NO 的浓度有所降低。这表明EDC-GRI 3.0 耦合模型能够准确预测NO 轴向轮廓，且模型对NO 质量分数峰值的预测位置与实测值吻合较好。

综上所述，EDC-GRI 3.0 耦合模型是一个准确且可靠的燃烧动力学模型，可以用来模拟燃烧过程中湍流化学相互作用，可以准确地预测温度和组分浓度。

3 助燃空气对NO生成的影响

助燃空气是关乎裂解炉污染物排放量的重要影响因素[27]。一方面，在裂解炉中适当提高空气预热温度会促进燃料的燃烧，降低化学不完全燃烧损失，提高裂解炉的热效率[28-29]，但空气预热温度提高将同时增加NO 排放量。为达到保证裂解炉的热量需求又降低NO 的效果，需要寻求一个最佳的空气预热温度来使两种需求达到平衡。另一方面，在低过量空气系数下的燃料会充分燃烧，不仅减少了NO 的生成率，还提高了裂解炉的热效率。但是，如果过量空气系数过低，会增加CO 的生成率并降低热效率，因此对过量空气系数有最低限度。本文采用CHEMKIN[30]和CFD 相结合的方法探究裂解炉中空气预热温度和过量空气系数对NO 排放的影响，分析比较不同工况下的热效率和NO 产生率，寻求一种最优的助燃空气模型。

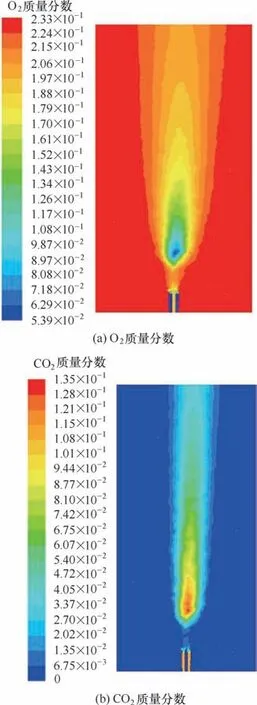
图5 Flame D组分分布云图Fig.5 Species distributions contours of Flame D

3.1 模型建立

图6 NO质量分数分布Fig.6 NO mass fraction distribution

本文以某工业乙烯裂解炉为研究对象。本部分的主要目的是比较在不同空气预热温度和过量空气系数条件下炉膛内燃烧排放的NO 生成量及产生速率影响，为了节省计算时间和资源，没有对炉管内裂解反应的吸热过程进行模拟[1,31-32]。在保证计算精度的前提下，使用化学反应动力学软件CHEMKIN-PRO 计算不同的空气预热温度和过量空气系数对NO 产生的影响。燃烧反应动力学模型采用第2部分验证的GRI 3.0简化机理。表2是炉膛结构和操作条件。

表2 裂解炉炉膛结构尺寸和操作条件Table 2 Structure dimension and operating conditions of cracking furnace

3.2 空气预热温度对NO生成的影响

图7显示了空气预热温度分别为300、350、400、450、500、550、600、670、740、810、890 和960 K 工况下燃烧器上方烟气平均温度和NO 的分布规律。随着燃烧空气的预热温度逐渐升高，烟气的平均温度有着显著的升高，这表明，随着空气的预热温度升高，燃烧反应速率加快，这有助于燃料的完全燃烧和温度分布的均匀性。但随着温度的升高，受高温影响热力型NO 产生量将远大于燃料型NO，燃烧器内的NO 迅速累积。从图中还可以看出，当预热温度大于600 K时，NO的摩尔分数显著上升。

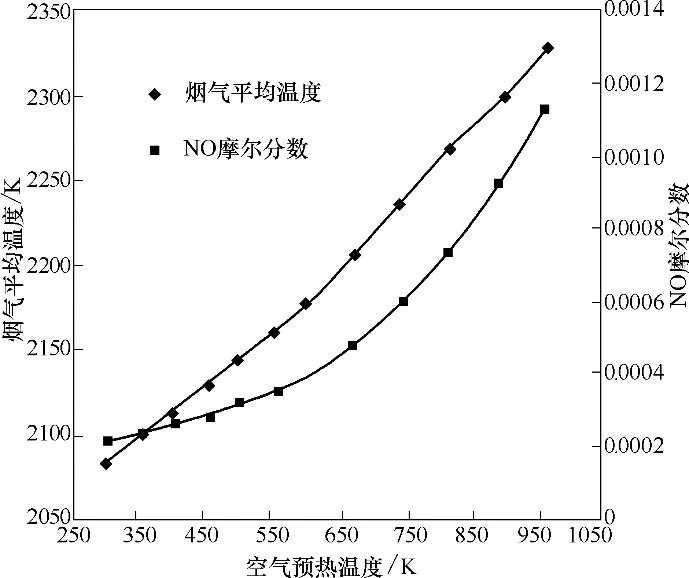
图7 不同空气预热温度下燃烧器上方烟气平均温度和NO分布规律Fig.7 Flue-gas average temperature and NO distribution above burners at different preheating temperatures

图8 为不同空气预热温度下NO 的摩尔生成率和质量流率分布。随着燃烧室的平均温度升高，空气的预热引起了NO 排放量增加。NO 的生成速率和质量流率随着燃烧空气预热温度的升高呈指数关系增大。当预热温度低时，NO 浓度增长不快，但当温度持续升高且超过600 K 时，NO 的生成率显著增加且浓度累积更快，这表明空气预热温度对NO排放有很大的影响。在保证燃烧火焰的稳定和燃烧器热效率的前提下，同时考虑到过高的空气温度对燃烧器的寿命影响，因此，裂解炉的空气预热温度应控制在600 K以下。

3.3 过量空气系数对NO排放的影响

图8 不同空气预热温度下的NO摩尔生成率和质量流率Fig.8 Mole production rate and mass flow rate of NO at different air preheating temperatures

裂解炉燃料实际燃烧空气量与理论空气量的比值为过量空气系数，用α表示。当裂解炉的α＜1时，将造成燃料不完全燃烧，降低裂解炉热效率；α过大时，会降低火焰最高温度，使辐射传热能力变低，进而影响NO 的产生率。本文主要模拟了质量流量为1.05、1.07、1.09、1.10、1.13、1.16、1.20 的七种工况，旨在寻找出乙烯裂解炉的最优α值范围。由于裂解炉燃烧器混合方式不同，当使用不同的过量空气系数后，风门入口流量、侧壁烧嘴流量都会相应改变，计算后的不同过量空气系数下的入口条件如表3 所示。

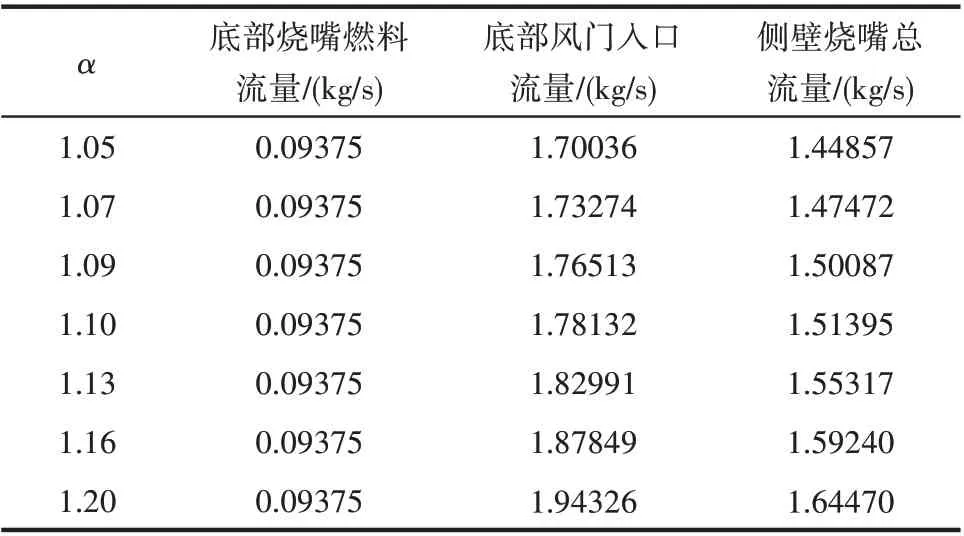
表3 不同过量空气系数下的入口条件Table 3 Inlet conditions under different excess air coefficients

表4 表示使用CHEMKIN 计算的不同过量空气系数下的模拟结果。从表中可以看出，当过量空气系数＞1 时，火焰最高温度随着α的增加而降低。这是因为当α＞1 时，随着过量空气系数增加，不参与燃烧的空气量增加，并且这部分空气带走大量热量，从而降低火焰温度。从表中还可以看出，较大的过量空气系数会使燃料放热量减少，使燃料CH4剩余量增多，从而降低了燃烧器的热效率。

表4 不同过量空气系数下的模拟结果Table 4 Simulation results under different excess air coefficients

图9 表示不同过量空气系数下的NO 摩尔生成率和反应净生成热曲线。当燃料释放的热量越大，燃烧越充分，热效率越高。图9表明，当过量空气系数从1.05 增大到1.1 时，模拟出的NO 产生率的减小速度明显高于过量空气系数大于1.1 时的NO 生成率减小速度。而当α由1.05 增大到1.1 时热效率下降速度缓慢，α大于1.1时燃烧器的热效率下降速度突然加快。为保证裂解炉不仅要降低NO 排放的要求，更重要的是保证足够多的燃料放热量为管内的裂解反应提供必要的热量，确保目标产物的收率。因此，过量空气系数为1.1 时基本可以满足较高的裂解炉热效率和较低的NO排放量的要求。

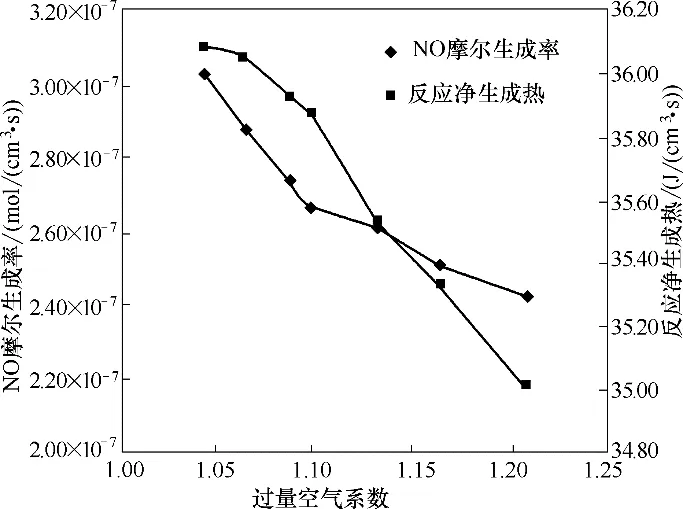
图9 不同过量空气系数下的NO摩尔生成率和反应净生成热Fig.9 NO molar production rate and net heat production of reaction under different excess air coefficients

3.4 空气预热温度与过量空气系数的综合影响

根据3.2 节和3.3 节的结论，在FLUENT 中采用与2.3 节相同的流动、辐射和燃烧模型对空气预热温度为400 K、过量空气系数为1.1 的工况进行数值模拟，得到NO 浓度分布。并与某典型工业生产工况[15]（空气预热温度为环境温度300 K、过量空气系数1.05）的NO 浓度分布进行比较。图10 和图11 分别显示了两种工况下沿炉膛高度方向的NO 摩尔分数云图和平均NO摩尔分数分布。图12显示了两种工况下炉膛出口处的NO 质量分数分布云图。从图中可以清晰地看到当空气预热温度为400 K、过量空气系数为1.1时能明显降低NO的排放。

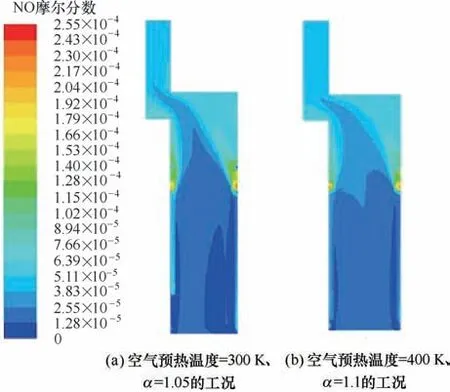
图10 两种工况下沿炉膛高度方向NO摩尔分数分布Fig.10 NO molar fraction distribution along furnace height under two conditions

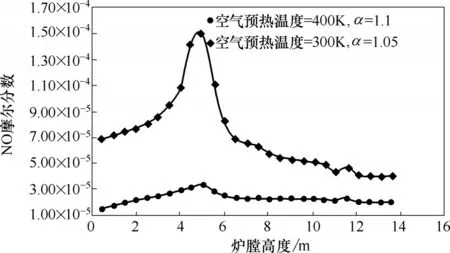
图11 两种工况下沿炉膛高度截面的平均NO摩尔分数分布Fig.11 Average NO molar fraction distribution along furnace height section under two conditions

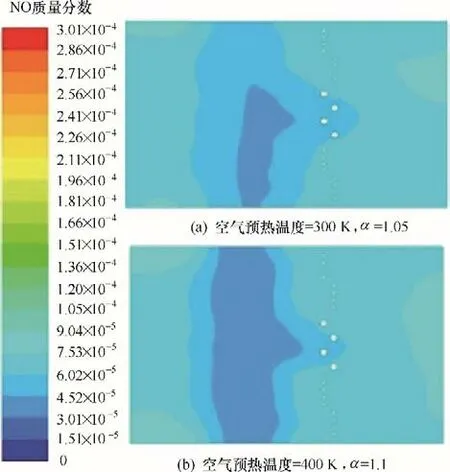
图12 两种工况下炉膛出口处的NO质量分数分布Fig.12 NO mass fraction distribution at furnace outlet under two conditions

4 结论

(1)采用EDC 燃烧模型与简化机理GRI 3.0 联合模拟的方法模拟标准Flame D 湍流扩散的燃烧过程，仿真结果验证了GRI-Mech 3.0 简化机理预测NO 排放的准确性和EDC-GRI 3.0 耦合模型的可靠性。

(2)考察不同空气预热温度和不同的过量空气系数对裂解炉NO 排放的影响，确定最优工况范围为空气预热温度300～600 K，过量空气系数1.1。使用CFD 对改进工况与实际工况的裂解炉NO 浓度分布进行数值模拟，结果表明：当空气预热温度在400 K、过量空气系数为1.1 时，既可以满足裂解炉的热效率，又能达到减少NO排放的目的。

符号说明

I——辐射强度，J/(m2∙s)

K——湍动能,m2/s2

n——折射指数

Ri——由化学反应引起的组分i净产生率, mol/(cm3∙s)

r——位置矢量

Sφ——源项

s——方向矢量

s'——散射方向矢量

T——温度,K

Uj——j方向的速度分量,m/s

xj——j方向的坐标,m