位置社交网络中谱嵌入增强的兴趣点推荐算法

刘真，王娜娜，王晓东，孙永奇

（北京交通大学计算机与信息技术学院，北京 100044）

1 引言

基于位置的社交网络（LBSN,location-based social network）中不仅包含原有传统社交网络中的社交网络关系和用户标注信息，还包含基于GPS 服务收集的用户签到位置轨迹及相关位置的标注信息[1]。用户的移动行为模式、行动轨迹呈现一定的规律及特点[2]。随着LBSN 服务中用户数量的增加，包含多维度信息的LBSN 签到数据信息量也急剧增加，感兴趣的位置点（POI,point of interest）推荐成为LBSN 中的重要研究方向。为了满足用户寻找感兴趣地点的需求，POI 推荐使用用户历史签到位置、轨迹等一系列时空信息预测用户当下可能感兴趣且尚未访问过的位置[3]，例如酒店、餐厅、博物馆、商场等。

LBSN 中的多维度签到信息包括用户地理位置（Geo）、时间（temporal）、POI 类别信息和社交关系[4-7]。通过对LBSN 数据的深度挖掘，可以揭示更深层次的用户的POI 偏好。利用这些信息为用户推荐POI 可以有效帮助用户过滤掉不感兴趣的位置点，提高推荐准确率。

目前基于LBSN 的POI 推荐研究采用的模型主要有基于矩阵分解的协同过滤模型、概率模型以及神经网络模型。Cheng 等[8]综合考虑地理因素和社交因素，使用多中心高斯模型对地理因素建模，使用概率矩阵分解处理社交因素，最后将这两者融入广义矩阵分解框架中。Zheng 等[9]提出了一种新的概率方法，从用户签到记录挖掘隐藏的主题，基于该主题采用跨区域协同过滤方法以推荐新的POI。

近年来，神经网络应用于推荐系统中并取得较大进展。Ma 等[10]为融合上下文信息（如社交信息、地理信息等）和对用户-POI 之间的交互进行非线性建模，提出了一种基于自动编码器的模型。Zhao 等[11]提出了一种最大边际度量地理社交多媒体网络表示学习框架。Yang 等[12]将协同过滤与半监督学习相结合提出了一种基于神经网络的模型PACE（preference and context embedding），该模型通过对相邻用户和POI 进行平滑缓解数据稀疏，构造上下文信息图以共同学习用户和POI 的嵌入，从而预测用户对POI 的偏好。Ying[13]等提出了一种基于秩的方法PGRank，它将用户地理偏好和潜在偏好集成到贝叶斯个性化排名框架中。

现有研究中还存在以下2 个问题。

1)LBSN 中包含丰富的签到、社交等上下文信息，现有的融合上下文信息的推荐模型如果不能很好地捕捉数据的多维空间特性，将难以准确地捕获用户最近邻。

2)矩阵分解模型中用户对POI 的交互被处理为其潜在特征向量的内积，而内积只反映了潜在空间中向量之间的线性关系，忽视了用户和POI 之间存在的非线性交互[14]。

基于上述分析，本文提出谱嵌入增强的POI 推荐算法PSC-SMLP（preference enhanced spectral clustering and spectral embedding enhanced multi-layer perceptron）。该算法由两部分组成：偏好增强的谱聚类算法PSC 和谱嵌入增强的多层感知机SMLP。一方面，与传统的社交网络推荐算法不同，LBSN 丰富的信息有助于捕获用户之间的偏好紧密程度。因此，借助谱聚类能在任意形状的样本空间上聚类且收敛于全局最优解的优点，提出了融合上下文信息的偏好增强的谱聚类算法PSC，以更准确地获得用户最近邻，便于更好地学习用户对POI 的偏好。另一方面，本文提出谱嵌入增强的神经网络SMLP，通过捕捉用户和POI 的二分图关系进行谱嵌入，以增强MLP（multi-layer perceptron）学习用户与POI 之间的非线性交互能力。使用谱聚类后用户最近邻所形成的用户-POI 对的拼接向量作为SMLP 网络的输入，通过谱嵌入和神经网络的网络结构和非线性激活函数对用户与POI 之间的复杂交互进行非线性建模，以学习用户的POI 个性化偏好。

2 融合上下文信息的POI 推荐模型框架

2.1 问题描述

对融合上下文信息（签到信息、社交信息）的POI 推荐定义如下。

定义1用户签到。假设u 为用户，p 为POI，uID为用户u 的ID 标识，pID为p 的ID 标识，则用户u 在位置点p 的一次签到可以用一个三元组来表示：，其中，t 为签到时间。进一步地，用户u 的签到POI 集合可以表示为

定义2社交关系。是指用户之间互为好友，对于一对互为好友的用户u 和用户v，他们之间的社交关系可以用一个二元组来表示，即。进一步地，用户u 的好友集合可以表示为。

定义3POI 推荐。给定用户u 及其签到的POI集合Pu和好友集合Fu，POI 推荐为预测用户u 对所有未有签到记录的POI 点p 的偏好值，按偏好值排序的前K 个POI 则为对用户u 推荐的结果。

2.2 PSC-SMLP 推荐模型框架

本文提出的PSC-SMLP 模型框架如图1 所示。图1 中，通过设计偏好增强的谱聚类算法PSC 提出SP 相似度从用户签到偏好和社交偏好2 个方面捕捉数据的多维空间特性，更准确地捕获用户最近邻，继而使用谱聚类获得用户群组；进一步构造谱嵌入增强的神经网络SMLP 挖掘用户和POI 的非线性交互。SMLP 共分五部分，分别是输入层、谱嵌入层、拼接层、隐藏层和输出层。将用户群组中的用户-POI 标记对输入谱嵌入层，通过用户和POI 二分图的谱进行潜在因子建模，获得用户和POI 的谱特征向量表示。然后，将用户和POI 谱特征向量进行拼接，构造拼接向量作为隐藏层的输入，使用多个隐藏层深度模拟用户和POI 之间的交互。最后采用softmax 层作为输出层产生用户对POI 的偏好预测。

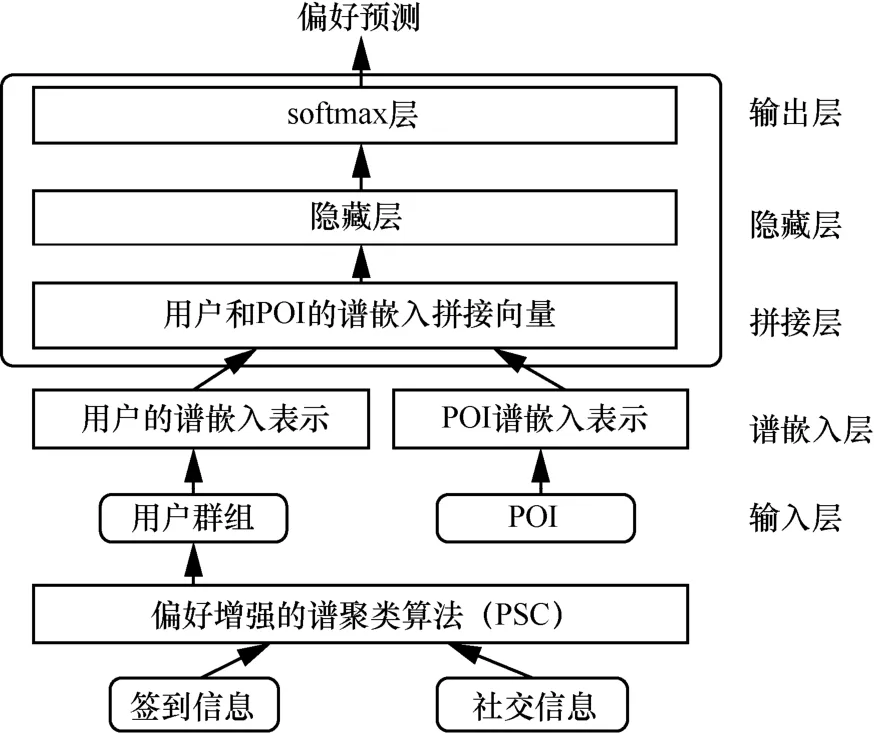
图1 PSC-SMLP 模型框架

3 偏好增强的谱聚类算法PSC

LBSN 中用户与用户之间的关系可以表示为社交网络图G，如图2 所示。图G 中的顶点有两类，分别是用户和POI；边有三类，分别为用户之间表示社交关系的边，用户和POI 之间表示签到关系的边，POI 之间表示关联关系的边。

图2 LBSN 社交网络G

以LBSN 标准离线数据集 Brightkite 为例，对其社交信息的分析结果分别如表1 和图3 所示。

表1 社交信息分析结果

图3 社交信息分析统计结果

从表1 中可知好友之间的平均共同签到数量远大于非好友之间的平均共同签到数量，这反映出好友之间有更大的签到相似性。图3 中，纵坐标是用户数量，横坐标表示用户访问其好友曾经访问过位置的概率，即用户第一次访问该位置之前该位置已被其好友访问过的概率。由图3 可知，用户初次访问的位置中90%以上曾被其好友访问过的用户数量位居第三。

经过上述分析可知，社交好友之间拥有更相似的签到偏好，用户在选择新的访问地点时，更偏向于访问其好友访问过的位置。

因此，本文从签到偏好和社交偏好两方面挖掘用户偏好的相似程度，构造偏好相似矩阵，继而采用常用于图领域、可识别任意形状空间并且能收敛于全局最优解的谱聚类算法挖掘用户最近邻，提出了偏好增强的谱聚类（PSC）算法。

3.1 PSC 算法

PSC 算法框架如图4 所示。

图4 PSC 算法框架

PSC 算法详细步骤如下。

1)偏好提取归一化相似度矩阵W

图2 中用户和用户之间的边定义为偏好相似程度，本文提出同时考虑签到关系和好友关系的sp相似度来度量用户与用户之间的边权值，如式(1)～式(3)所示。其中，式(1)中代表u1和u2共同签到的POI个数，up 表示两用户的兴趣偏好相似度的程度；式(2)中代表u1和u2共同好友个数，uf 表示两者的好友关系程度；式(3)中sp 相似度由up 和uf两部分的乘积计算得到。进一步采用随机游走的思想将用户和用户之间的相似度进行归一化，构造用户与用户的相似度矩阵U 以作为归一化的相似度矩阵W，如式(4)所示。

2)归一化的Laplacian 矩阵Lsym

谱聚类算法将聚类问题看作图分割问题，图分割的最优化问题与求解Laplacian 矩阵特征向量问题等价，因此要得到用户相似度矩阵对应的Laplacian矩阵。本文归一化的相似度矩阵W 为对称矩阵，故选择归一化Laplacian 矩阵Lsym，根据式(5)可以计算得到。

其中，D 为W 的对角矩阵，L=D-U。通过特征值处理，获得用户相似度矩阵对应Laplacian 矩阵Lsym的特征向量矩阵VT=[x1,x2,…,xn]，采用K-means对VT中的列向量进行聚类，聚类结果中x1,x2,…,xn分别所属的类别对应用户所属的类别。将隶属于相同类别的用户归为一个群组，从而获得用户最近邻构成的群组。

3.2 PSC 算法伪代码

PSC 算法伪代码如算法1 所示。

算法1PSC 算法

输入用户签到矩阵R、社交矩阵S

输出用户群组

4 SMLP 神经网络设计

一些研究进展[10-12]证明了神经网络在处理信息检索和推荐任务中挖掘用户和物品之间非线性潜在关系的有效性。

本文构建了谱嵌入增强的神经网络SMLP，网络结构如图1 所示。SMLP 的网络结构包括输入层、谱嵌入层、拼接层、隐藏层和输出层。通过PSC 算法获得的用户群组及其签到过的POI 形成用户-POI 对分别输入到谱嵌入层，将获得用户和POI 的谱嵌入表示，通过拼接层，获得用户-POI 对的谱嵌入式拼接向量。在隐藏层中，对拼接向量进行学习，最后在softmax 层输出用户对POI 的偏好预测。

4.1 谱嵌入层

图2 中的用户和POI 之间的签到关系可以表示为二分图，包含丰富的用户和POI 的直接或间接连通信息，间接隐含的连通度对挖掘偏好也具有重要意义。图的谱侧重于反映图的连通性，有助于更好地挖掘潜在连通性。

图的谱即是图拉普拉斯矩阵的特征向量所组成的矩阵[15]。本文提出的谱嵌入层通过连通信息图的谱对用户和POI 进行谱映射，从而获得用户和POI 的谱嵌入向量。具体设计如式(6)所示。

其中，SE=Efα(Λ)ET，Λ=diag {λ1,λ2,…,λn}，fα(Λ)==diag{α1λ1,α2λ2,…,αnλn}。E 和Λ分别是用户-POI签到二分图对应拉普拉斯矩阵的特征向量矩阵和特征值矩阵，fα(Λ)对特征值进行参数化以获得更好的特征表示，eu和 ep是指定嵌入维度使用高斯分布随机初始化的用户特征向量和POI 特征向量，分别代表用户谱嵌入向量和POI 谱嵌入向量。

4.2 其他各层的设计

本文使用神经网络来拟合输入用户-POI 对和输出POI 预测结果之间的关系。本文选用非线性激活函数，通过隐藏层层数的不断加深可以使神经网络逼近任意复杂函数，从而可以更加明确地描述输入与输出之间的关系，并将神经元的输出映射到有界的区域。

因此，SMLP 神经网络各层的输出为

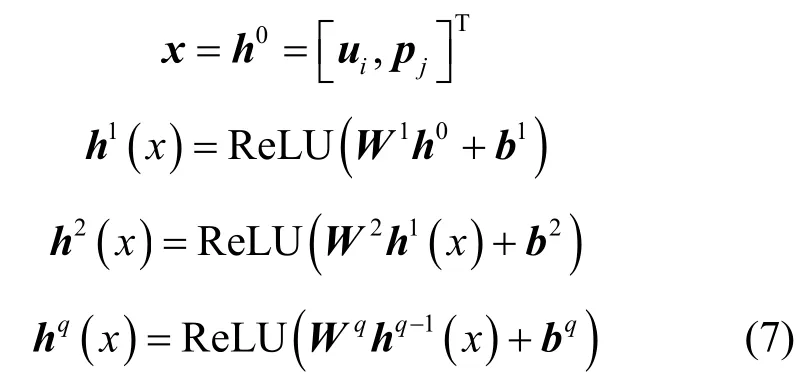
其中，Wq，bq是第q 层的参数。当q=0 时，x 为用户-POI 对的拼接向量。

POI 推荐属于OCCF（one class collaborative filtering）问题[16]。为了特别处理POI 推荐中隐式反馈的单类性质，在隐藏层的顶部连接了一个二进制softmax 层。softmax 层是一个使用sigmoid 函数的逻辑回归层，因此在输入层也使用sigmoid 函数来获得用户对POI 的偏好程度，如式(8)所示。

本文选用对数损失函数（logloss）作为SMLP神经网络的目标函数，如式(9)所示。

5 实验及结果分析

5.1 实验设置

5.1.1 数据集分析

本文实验部分数据集采用的是LBSN 中2 个经典的数据集（Gowalla 和Yelp）。

Gowalla 数据集为斯坦福大学研究人员在Gowalla 平台上获得的2009 年2 月至2010 年10 月在全球范围内生成的真实签到数据。过滤掉签到POI 次数少于15 的用户及被签到次数少于10 的POI，过滤后的数据集包括18 737 个用户，32 510 个POI，1 278 274 次签到。平均每个用户签到68 个POI，每个POI 被40 个用户签到过。

Yelp 数据集包含大量的POI 和若干个城市内的签到记录。过滤掉签到POI 次数少于10 的用户，过滤后的数据集包含30 887 个用户，18 995 个POI和860 888 次签到。平均每个用户签到27 个POI，每个POI 被45 个用户签到过。

Gowalla 和Yelp 数据集中都包括好友关系和签到记录，其中互为好友关系的用户成对出现。对数据进行预处理后的基本信息如表2 所示，表中稀疏度表示为用户-POI 签到次数矩阵中空白项和所有项的比例。

表2 数据集基本信息

针对Gowalla 和Yelp 这2 个数据集，对用户签到POI 数量和POI 被签到的用户数量进行统计，如图5 所示。图5 中纵轴表示参与统计的用户数量或POI 数量，横轴表示签到数量。

图5 N1和N2的数量

将用户签到POI 数量标记为N1，POI 被签到用户数量标记为N2。从图5 可看出在Gowalla 数据集上用户签到POI 数量为31～51 的用户数目最多，而在Yelp 数据集上，用户签到POI 数量范围为0～20的用户数量最多。

5.1.2 对比算法

本文采用以下 8 个算法与本文提出的PSC-SMLP 算法进行对比。

1)iGSLR（personalized geo-social location recommendation）[17]。使用KDE（kernel density estimation）为用户签到行为的地理因素进行个性化建模，然后将用户偏好、社交和地理因素融合到统一的框架中。

2)LFBCA（location-friendship bookmark-coloring algorithm）[18]。基于4 种因素，分别为用户的历史行为、地理因素、社交因素和相似用户，使用PPR（personalized page rank）算法，计算过程使用书签着色算法（bookmark-coloring algorithm）。

3)LORE（location recommendation）[19]：从用户的签到行为中挖掘顺序影响，将顺序、社交和地理影响融合到统一的推荐框架LORE 中。

4)USG（user social geographical）[20]。考虑到用户偏好、社交及地理影响，分别使用UserCF（user collaborative filtering）、FCF（friend collaborative filtering）和幂律分布对其进行建模，最后将多个模型融合到统一的推荐框架USG 中。

5)IRenMF（instance-region neighborhood matrix factorization）[21]。通过将相邻特征合并到加权MF（matrix factorization）中来对地理影响建模。

6)ASMF（augmented square error based matrix factorization）和ARMF（augmented ranking error based matrix factorization）[22]。考虑到社交影响、分类影响、地理影响，提出了基于平方误差的MF 模型和基于增强的排名误差的MF 模型。

7)PACE（preference and context embedding）[12]。考虑到LBSN 中的多种上下文因素（重点是社交影响和地理影响），将协同过滤和半监督学习相结合提出了一种通用的推荐框架。

8)LOCABAL（local and global）[13]。利用2种社会关系社交朋友和全球声誉较高的用户使用MF 进行建模。

本文使用了4 个评价指标用于衡量算法的性能，即准确率（Pre@K）、召回率（Rec@K）、归一化折扣累积增益（nDCG@K）和平均精度（MAP@K），其中，K 表示推荐列表的大小。

5.2 参数设置实验

采用留一法方案[12]，根据文献[23]的策略为每个用户真实签到的POI 随机选择100 个未签到的POI 作为负样本，然后将真实签到的POI 和负样本混合构造测试集。

5.2.1 PSC 中聚类簇数k 的设置

本文选择常用的聚类评估指标。CH 指标（Calinski-Harabaz index）分数来进行聚类簇数k 的评价。CH 指标分数越大说明聚类效果越好。

对于k 个簇，CH 指标分数由簇间离散平均值与簇内离散之比得出

其中，N 是数据集的数量，Bk是簇内离散矩阵，Wk是簇间离散矩阵。Bk和Wk的定义如式(11)和式(12)所示。

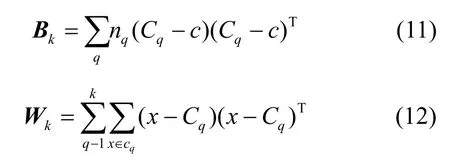
其中，Cq是簇q 的中心，c 是数据集的中心，nq是簇q 的数据点的数量。

假设k 分别为2、5、8、10、15，对数据集Gowalla和Yelp 使用CH 指标分数来评估聚类效果，结果如图6 所示。从图6 中可以看出，对于数据集Gowalla，当聚类簇数k 为8 时聚类效果最好。对于Yelp 数据集，当k 为2 时，聚类效果最好，但是考虑到该数据集的整体平均情况，选择聚类效果次优的k=8 的值。因此，设置聚类簇数k 为8。选用用户数量最多的群组分别进行后续实验，最后在Gowalla 和Yelp 数据集上分别选用用户群组2 和用户群组1，这2 个群组的用户数量分别为8 302 和9 233。

图6 聚类簇数k 对聚类效果的影响

5.2.2 神经网络结构的评估

本文通过改变神经网络架构中隐藏层的层数以及每个隐藏层的容量（即神经网络的深度和宽度）来讨论PSC-SMLP 中学习用户偏好的有效性。

本文设置用户和POI 嵌入到共享维度空间[16]。输入层是用户和POI 的联结向量，所以隐藏层的输入层容量是2 的倍数，受文献[12]启发，将隐藏层以2 的指数衰减进行架构的设计。

1)首先令聚类簇数k=8，按照32→16→8→4设计神经网络的架构（为避免过饱和，设置较为适中的网络结构），设推荐列表数量为10，以Gowalla为数据集讨论迭代次数对于损失函数值loss 和命中率HitRatio@10 的影响，如图7 所示。从图7 中可以发现随着迭代次数的增加，训练目标函数的loss越来越小，且在迭代次数为20 时，loss 急剧下降。综合考虑HitRatio@10 和loss，本文将迭代次数设为50。

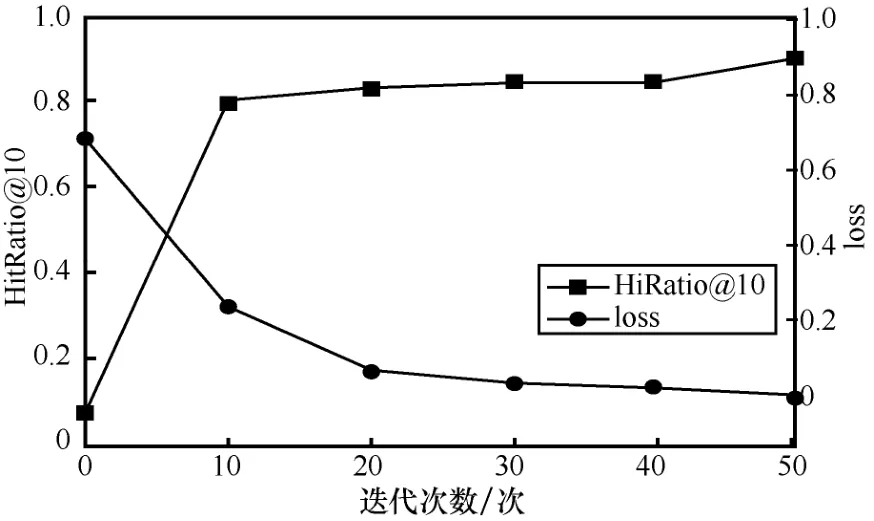
图7 迭代次数对命中率和损失值的影响

2)在 Gowalla 数据集上对所有数据使用accuracy 来评估神经网络深度和宽度的影响。accuracy 通过预测值和实际值之间差值来衡量神经网络在不同网络结构下的训练效果，如表3 所示，其中h 为神经网络层数。

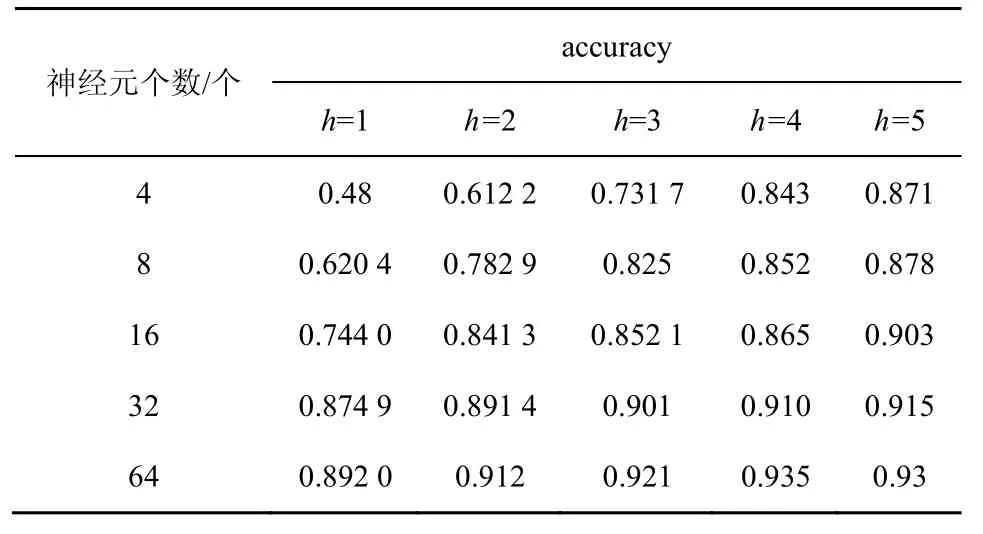
表3 不同神经网络结构的accuracy

设置其它参数，如学习率为0.000 1。从表3 中可以看出，当只使用一层神经网络时，神经元的个数越多，accuracy 越高。一般来说，固定最后一层的容量大小，随着层数的增加，accuracy 增大。当最后一层的容量较大时，隐藏层层数的增加会给模型带来饱和，例如表3 中当层数为4，最后一层神经元的个数为64 时，本文提出的神经网络模型对于已固定的其他参数而言，达到了饱和状态。

5.3 性能比较

5.3.1 与对比算法的比较

图8 表示在Gowalla 和Yelp 这2 个数据集上PSC-SMLP 与其他算法的性能，PSC-SMLP 在各项指标上均优于其他模型。图8(a)～图8(d)所示在Gowalla 数据集上的各个算法性能均优于图8(e)～图8(h)所示在Yelp 数据集上的算法性能，这是因为Gowalla 数据集的签到信息和社交信息较Yelp数据集更为丰富，充分表明利用PSC 融合上下文信息给模型带来的优势。

图8 Gowalla 和Yelp 数据集上的性能对比

对比算法中PACE 属于神经网络模型，其他算法模型都是基于传统的协同过滤矩阵分解模型。PSC-SMLP 和PACE 在各指标上性能的优越性充分表明了神经网络结构和非线性激活函数对于复杂交互场景下的学习能力。PSC-SMLP 在Gowalla 数据集 Rec@K 中平均提高约3%，最高达13%。在Pre@K 中提高最高达1.9%。在Yelp 数据集中Rec@K 中平均提高约4%，在Pre@K 中提高最高达2.1%，从在同一数据集上算法的性能提升来看，PSC-SMLP 算法在稀疏数据集上比PACE 模型的有效性更明显。一方面是因为PSC 不仅从用户签到偏好和社交影响2 个方面捕捉相似用户获得用户群组，而且从聚类角度缓解数据稀疏；另一方面，模型的SMLP 部分有效地利用神经网络和非线性激活函数的优势捕获用户和POI 之间的复杂交互，更好地学习了用户偏好。

充分利用签到信息和社交信息，更有利于提高算法的性能。PSC-SMLP 在Gowalla 上的平均性能比IRenMF 提高约3%，其中，在Recall@10 上的改进高达7.9%。在Yelp 数据集上，PSC-SMLP 优于IRenMF 约3.2%，可以发现PSC-SMLP 在稀疏度更大的Yelp 数据集上实现的性能提高优于在Gowalla 数据集上实现的提高，这也说明利用更多的上下文信息，PSC-SMLP 可以缓解数据稀疏。

5.3.2 PSC-SMLP 与SMLP 的比较

在Gowala 数据集和Yelp 数据集上，从Pre@K和Rec@K 这2 个指标来对比PSC-SMLP 和SMLP算法，以衡量PSC 谱聚类所起的作用，如图9 所示。从图9 可以发现，PSC-SMLP 在2 个指标上均优于SMLP，在 Gowalla Pre@K 上，性能提升约为0.2%～1.6%；在Gowalla Rec@K 上性能最高提升约为2.11%。在Yelp Pre@K 指标上PSC-SMLP 性能提升约为0.5%～1.8%；在Yelp Rec@K 上性能最高提升约为3.08%。从这些数据中可发现，PSC-SMLP相比于SMLP 在Yelp 上性能改进均大于Gowalla。由此可知，在数据稀疏度大于Gowalla 的Yelp 数据集上，PSC 能更有效地捕捉数据的多维空间特性，准确地定位用户最近邻。

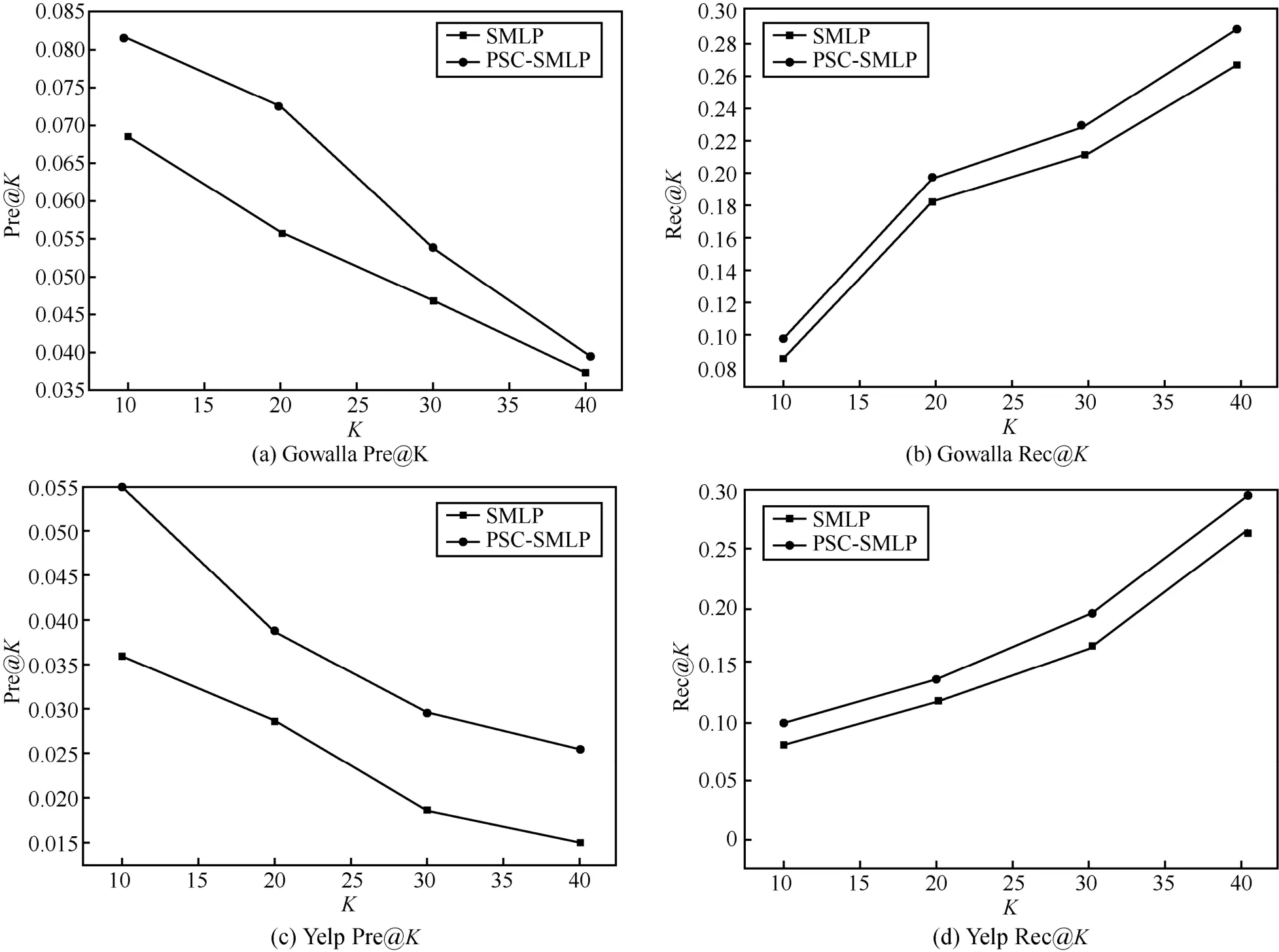
图9 PSC-SMLP and SMLP 的对比

6 结束语

LBSN 中丰富的上下文信息（签到信息、社交信息）为充分学习用户偏好，提高POI 推荐算法的准确率提供了机遇。然而将上下文信息直接融入到推荐模型中会引起数据维度增大，也将增加用户和POI 非线性交互的挖掘难度。本文提出了一种新的POI 推荐算法PSC-SMLP。在图模型基础上提出了偏好增强的谱聚类算法PSC 进行用户偏好上下文的挖掘，PSC 可从用户偏好和社交偏好2 个方面捕捉用户对POI 签到的相似性，基于谱聚类的PSC 也能在多维数据构成的任意形状空间中具有良好的空间识别能力。本文进一步构造了谱嵌入增强的神经网络SMLP，谱嵌入层通过连通信息图的谱对用户群组和POI 进行谱映射，更好地捕捉用户和POI之间的连通信息，从而获得用户和POI 的谱嵌入向量，构造的深层网络结构和非线性激活函数基于谱嵌入层充分学习了用户对POI 的偏好。在Gowalla和Yelp 这2个数据集中与传统的协同过滤和复合模型算法进行了对比，在多个评价指标上，本文算法推荐性能更优。

更进一步的研究将考虑自注意力模型，从多个层次来捕获用户对不同POI 的关注度，以进一步提高推荐准确率。