16QAM-LFM 雷达通信一体化信号设计
2020-04-06曾浩吉利霞李凤李创
曾浩,吉利霞,李凤,李创
(重庆大学微电子与通信工程学院,重庆 400044)
1 引言
长期以来,雷达系统和通信系统作为2 个独立的系统被研究,但是这2 个系统又有很多相似之处。雷达系统的功能是实现目标探测、定位和跟踪,通信系统的功能是实现信源和信宿之间信息的传输。雷达通信一体化通过硬件共享和简化结构,降低了成本,减轻了电磁干扰[1]。在雷达通信一体化技术研究中,一体化波形设计是关键内容之一。早期Roberton 等[2]设计的一体化波形是先独立产生通信波形和雷达波形,再采用二者叠加的方式形成的。近年来,各种雷达通信一体化波形不断被提出。文献[3]提出了将最小频移键控(MSK,minimum frequency shift keying)信号与线性调频(LFM,linearly frequency modulated)信号结合的波形一体化设计方法MSK-LFM,把LFM 信号作为MSK 信号的载波。这种波形设计可以在现场可编程门阵列(FPGA,field programmable gate array)中具体实现[4]。但由于MSK-LFM 一体化信号采用的是低阶调制,通信速率较低,无法满足实际通信的需要。为了提高通信速率,目前主要采用多载波的方法,如文献[5-6]对正交频分复用(OFDM,orthogonal frequency division multiplexing)信号与LFM 信号相结合的OFDM-LFM 波形一体化设计方法进行了研究,这种设计方法存在2 个问题,一是雷达发射机发射功率大,峰均功率比高,从而引起波形失真较大;二是计算复杂度高。文献[7]提出了一种使用多频率补码相位编码序列与OFDM 系统相结合的一体化波形设计方案,计算量非常大。文献[8]设计了一种恒包络OFDM 雷达通信一体化方案,该方案将一体化信号分为通信调制项和雷达调制项,通过控制通信加权系数,在雷达和通信性能之间取得最佳折中。文献[9]用正交调频方案将通信符号嵌入雷达波形中,但需要加权系数来权衡误码率性能和模糊函数性能,权系数求解非常复杂。文献[10]提出了基于功率最小的雷达通信一体化系统,依然采用OFDM体制。文献[11]提出了基于多输入多输出的正交频分复用(MIMO-OFDM,multiple-input multiple-output-orthogonal frequency division multiplexing)的雷达通信一体化系统,提高了系统的分辨率和传输速率,缺点是实现难度大,成本高。本文提出了一种提高通信速率的方法,把16 阶正交幅度调制(QAM,quadrature amplitude modulation)信号与LFM 信号相结合构成16QAM-LFM 波形,具体方法是用线性调频信号作为16QAM 信号的载波。由于16QAM-LFM 波形采用了高阶调制,因此比BPSK-LFM、MSK-LFM 等低阶调制的一体化波形具有更高的频带利用率,并且比OFDM-LFM 的实现复杂度低。通过分析可知,16QAM-LFM 波形具有与16QAM 波形相同的通信误码率特性,同时也具有良好的雷达分辨率、虚警概率和检测概率。
2 16QAM-LFM 一体化信号设计
在高阶数字调制中,16QAM 已经被广泛使用,具有较高的通信传输速率。而LFM 脉冲也是雷达中的基本波形,能够解决雷达作用距离和距离分辨率之间的矛盾。把16QAM 信号和LFM 信号结合,可以保持两者各自的优点,构成新的雷达通信一体化波形。新波形也是脉冲波形,每个雷达脉冲中有一个16QAM 信号。但该16QAM 信号的载波并不是固定频率,而是 LFM 信号。16QAM-LFM 一体化信号实现过程如图1 所示。

图1 16QAM-LFM 一体化信号实现过程
图1 中,16QAM 信号可以通过两路独立正交的四进制振幅键控(ASK,amplitude shift keying)信号叠加产生。基带二进制序列 d(t)首先经过串并转换,形成两路并行的新二进制序列。然后通过进制转换,获得2 个支路的四进制基带信号 ao(t)和ae(t),其等概率取值为 ±1 或 ±3 。显然,此时四进制信号的速率已经降为原始二进制序列速率的。把基带信号与2 个正交载波相乘,并叠加两路信号,就形成了最终的16QAM-LFM 雷达通信一体化波形。
通常,固定频率载波16QAM 信号可以表示为
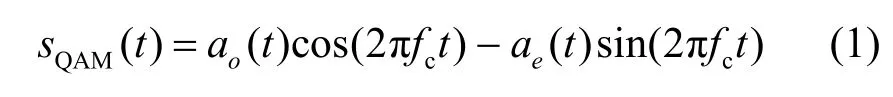
但在雷达通信一体化波形设计时,载波应该采用LFM 脉冲信号,即

其中,A 为幅度值;μ 为线性调频信号的调频率,其由雷达脉冲宽度T 和带宽B 决定,即

此时,最终的16QAM-LFM 雷达通信一体化信号的计算式为
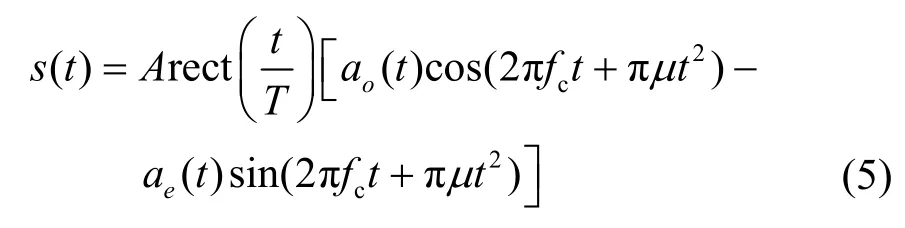
图1 中产生16QAM-LFM 信号的方法对于工程实现而言并不复杂。但是,考虑信号幅度种类增加,信号的动态范围变大,这就要求射频前端放大器的线性度较高,因此增加了成本。雷达通信一体化接收机由2 个并支路构成,一个支路是针对通信的解调,另一个支路则是针对雷达脉冲的检测。其中,通信接收采用相干解调,需要从脉冲信号中提取相干载波。该载波是一个LFM 信号,所以不能采用锁相环实现,而是采用参数估计的方式产生[12]。雷达脉冲检测的方法与传统雷达接收机并没有区别,只是匹配滤波器需要保持与发射脉冲波形一致。
3 性能分析
3.1 通信性能分析
3.1.1 误码率分析
分析16QAM-LFM 信号误码率时,根据式(5),可以视其为两路独立的4ASK-LFM 调制信号之和。所以,首先分析4ASK-LFM 调制信号的误码率。4ASK-LFM 信号经过高斯白噪声信道后的计算式为

其中,A 为幅度值,n(t)为带限高斯白噪声,其功率谱密度为N0。接收机采用相干解调,因此解调器输出信号为

其中,no(t)为输出高斯噪声,其平均功率为

其中,ρ 为接收机中低通滤波器的系统函数的能量。
接收机中,对4ASK-LFM 解调器输出电压值抽样判决,但由于噪声的影响会导致误码。平均误码率为
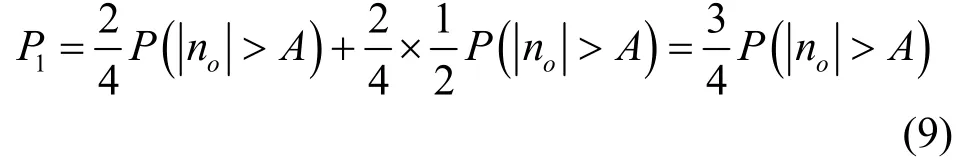

将式(10)代入式(9)中,可得

其中,误差函数为

另一方面,A 可以通过接收信号功率Ps表示。等概率的4ASK 信号的平均功率为

由式(13)可得

将式(14)代入式(11),单路4ASK-LFM 误码率为

由于16QAM-LFM 是两路正交的4ASK-LFM信号叠加,因此一体化波形的误码率为
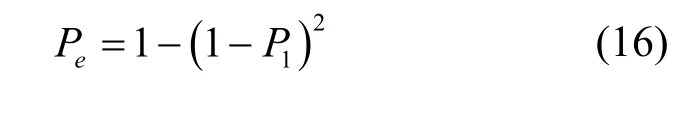
即
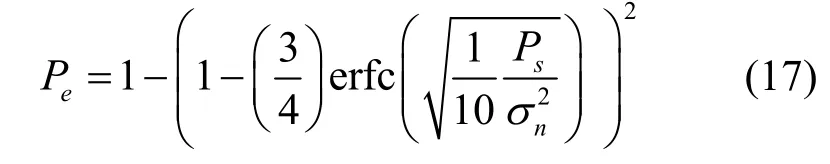
进一步地,4ASK-LFM 信号的功率为16QAM-LFM 信号功率的一半,可得16QAM-LFM信号的接收信噪比为

将式(18)代入式(17),可以得到16QAM-LFM一体化波形的通信误码率为

3.1.2 频带利用率分析
16QAM-LFM 信号相比采用低阶调制的雷达通信一体化信号,如BPSK-LFM 信号、MSK-LFM 信号,其频带利用率显著提升,这是因为16QAM 比BPSK 和MSK 具有更高的频带利用率。OFDM-LFM多载波调制信号的频带利用率与子载波调制方式有关,如果子载波采用QPSK 调制,16QAM-LFM和OFDM-LFM 具有相同的频带利用。不同一体化波形频带利用率对比分析如表1 所示。

表1 不同一体化波形频带利用率对比分析
虽然16QAM-LFM 的频带利用率提高了,但也需要付出一定代价。根据前文分析方法和结论,可以得到不同一体化波形误码率与接收SNR 关系,如表2 所示。另外,OFDM-LFM 信号的平均误码率与其子载波的误码率保持一致,由子载波采用的调制方式决定。从表2 中不难看出,高阶调制在一定程度上牺牲了误码率性能来提高频带利用率,即频带利用率越高,相同SNR 下误码率也越高。
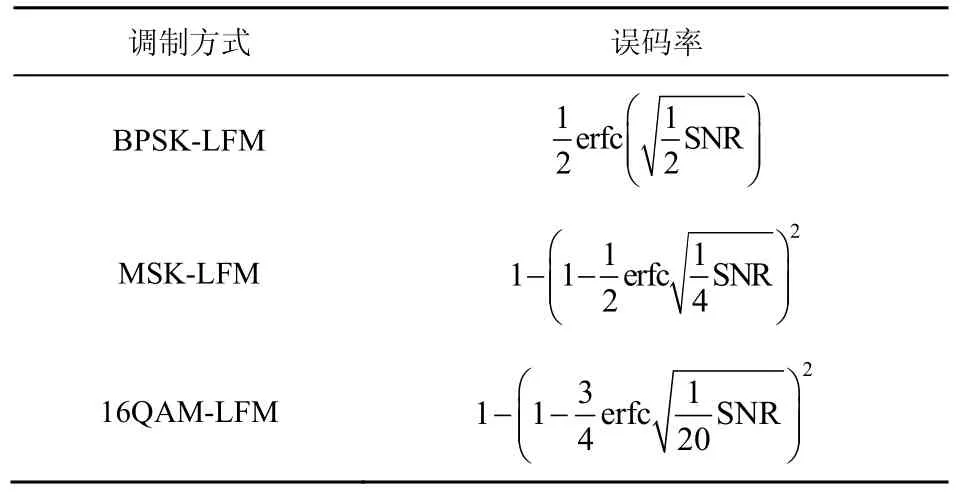
表2 不同一体化波形误码率与接收SNR 关系
3.2 雷达性能分析
3.2.1 模糊函数
模糊函数是描绘雷达波形距离分辨率和速度分辨率的关键性能指标,传统上定义为


显然,根据16QAM-LFM 的式(5)可以得到其归一化复包络为

其中,m(t)是由调制星座图确定的离散复随机变量,计算式为

把式(22)代入式(21)并交换积分与求均值顺序,得到
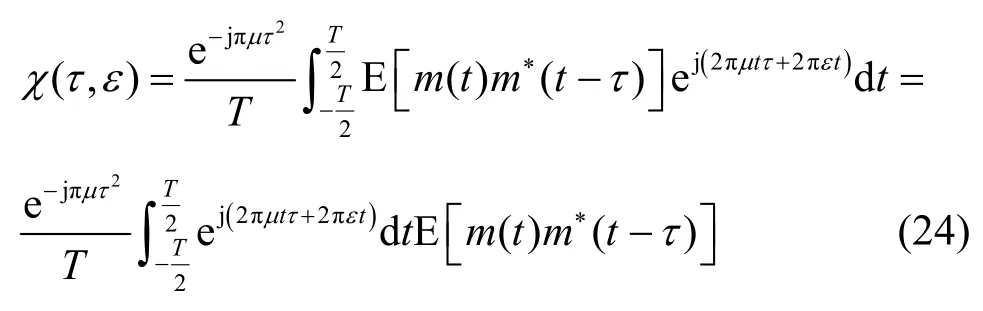

第二个因子根据自相关函数定义,并考虑 ao(t)和 ae(t)为独立且均值为0 的同分布随机变量,有

式(26)结果显示,构成一体化波形模糊函数的第一部分等于经典LFM 的模糊函数,为刀刃状;第二部分信息序列的自相关函数为图钉状,即只有在≤ Tb范围内才不为0,且越大,自相关函数值越小。因此一体化波形模糊函数接近图钉型,可以保持较好的分辨率。同时,图钉状的模糊函数也说明,在动目标情况下,16QAM-LFM 信号的多普勒容错性能相对于经典LFM 信号要差一些,原因是一体化信号的匹配滤波器输出与线性调频信号匹配滤波器输出相比,基带包络 m(t)不是矩形,而是随机起伏的分段函数,使式(26)的自相关函数曲线宽度变窄。虽然16QAM-LFM 信号多普勒容错性下降,但一体化波形设计目的主要是使雷达具有通信功能,所以牺牲了雷达对于高速动目标的检测性能。针对多普勒敏感的雷达信号,要解决失配问题,需要进行多普勒频移补偿。
3.2.2 虚警概率与检测概率分析
雷达接收信号经过系统函数为 ks(τ-t)的匹配滤波器,然后进行包络检波,在包络检波输出信号x(t)最大值时刻 t0取样,对回波进行判决。匹配滤波器系统函数由16QAM-LFM 一体化波形 s(t)决定,对于接收机而言是已知量。虚警概率的定义是接收信号 x(t)只有噪声出现时,样本值超过门限电压VT的概率。检测概率是接收信号 x(t)包含信号和噪声时,样本值超过门限电压VT的概率[14-15]。
对于低速目标,在只有噪声情况下,检波器输出的噪声电压r=x(t0)的概率密度函数为

其中,高斯噪声经过匹配滤波器输出功率为

其中,E 为输入信号s(t)能量。虚警概率定义为
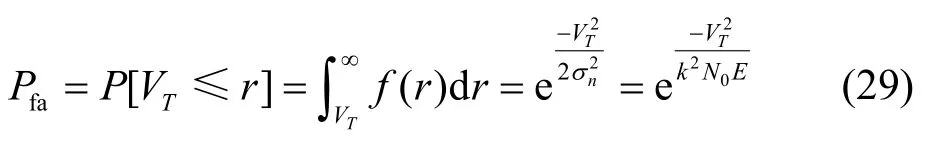
含噪声的一体化信号经过匹配滤波器后,同样经过包络检波器,输出信号r=x(t0)的概率密度函数为瑞利分布,即

其中,I0()为零阶贝塞尔函数。检测概率定义为
采用国际上公认的分类标准,将甲状腺癌患者肿大淋巴结内部血流分布分为Ⅰ~Ⅴ型,分别为淋巴口型、中央型、边缘型、混合型和无血流型,判断标准为Ⅰ型和Ⅴ型为良性特征,Ⅱ、Ⅲ和Ⅳ型为恶性特征。

为了进一步求解检测概率,在 t0时刻,不含噪声的有用信号功率为

所以,包络检波器输出最大瞬时信噪比为

根据Marcum Q 函数的定义
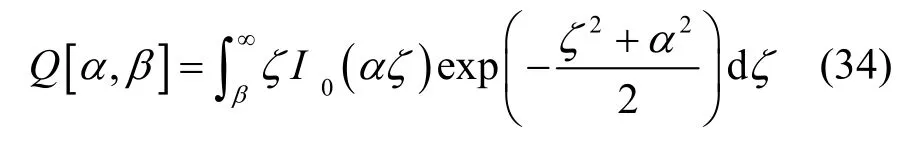
并结合式(29)、式(31)、式(33),检测概率可以表示为
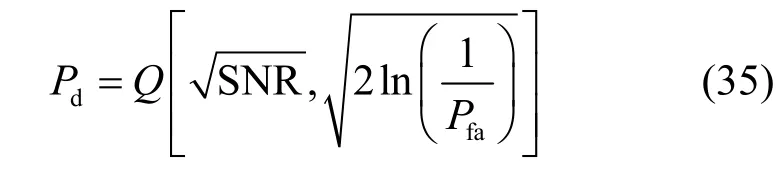
由式(35)可知,16QAM-LFM 信号与LFM 信号的检测概率的表达式相同,原因是匹配滤波器的输出只取决于信号的能量,而与信号的形式无关。从检测概率的表达式可以看出,当虚警概率一定时,信噪比越大,检测概率越大。
3.3 运算复杂度分析
在发送端,一体化波形产生的运算量主要来自数字调制信号的生成。对于16QAM-LFM 实现,根据图1 结构可知,仅仅需要2 个乘法器运算。而基于OFDM-LFM 的调制则需要进行混频和快速离散傅里叶反变换(IFFT,inverse fast Fourier transform)运算。显然OFDM-LFM 的实现复杂度在发射机更复杂。
在接收端,不同一体化波形雷达信号的处理是完全相同的,不同之处在于通信信号的解调。对于BPSK-LFM、MSK-LFM、16QAM-LFM 一体化波形解调,运算主要是由混频和滤波产生的,但在OFDM-LFM 波形解调中,除了混频和滤波所产生的运算外,还有FFT 计算产生的运算量。不同一体化波形接收端的计算复杂度比较如表3 所示,其中M 为滤波器阶数,N 为信号的采样点数,L 为码元个数。从表3 中可以看出,低阶调制运算量最低,而以QPSK 为子载波调制方式的OFDM-LFM 运算量要比16QAM-LFM 多 O(Nl b N)的运算量。

表3 不同一体化波形接收端的计算复杂度比较
4 仿真
4.1 通信性能仿真
仿真条件设置如下。信道为高斯白噪声信道,信噪比为0~18 dB,脉冲宽度为10 μs,脉冲周期数为250 个,符号率为4 M ·Symbol · s-1,载波频率为fc=3 GHz,中频频率fi=20 MHz,调频带宽B=10 MHz,采样率 fs=100 MHz,16QAM-LFM信号产生和解调采用第2 节中介绍的方法。误码率如图2 所示。根据式(19)结论,16QAM-LFM 的理论误码率和16QAM 完全相同,如图2 中实线所示,而通过仿真实验获得的真实误码率值如图2 中所示,二者基本重合。该仿真一方面说明了本文对16QAM-LFM 一体化波形误码率的推导结论是正确的,另一方面也说明16QAM-LFM 与传统16QAM 调制具有相同的通信性能。

图2 误码率曲线
同时,MSK-LFM 一体化信号和BPSK-LFM一体化信号的误码率仿真结果和理论曲线如图2所示。对比传统一体化信号 BPSK-LFM 和MSK-LFM,在相同的SNR 情况下,16QAM-LFM信号的误码率性能有所下降。因为在通信中,高阶调制时牺牲了一定的误码率性能来提升信号的频带利用率。
4.2 雷达性能仿真
4.2.1 模糊函数仿真
为了更容易判断和比较信号的分辨能力,在实际中,通常采用模糊图|χ(τ,ε)|2进行分析,并对模糊图进行归一化处理。对16QAM-LFM 信号的一个脉冲周期进行仿真,得到仿真结果分别如图3 和图4所示,图3 为16QAM-LFM 信号模糊图,图4 为16QAM-LFM 信号模糊图的等高线图。

图3 16QAM-LFM 信号模糊图

图4 16QAM-LFM 信号模糊图的等高线图
对传统LFM 信号采用相同的仿真参数,得到LFM信号的模糊函数仿真结果分别如图5 和图6 所示,图5为LFM 信号模糊图,图6 为模糊函数等高线图。

图5 LFM 信号模糊图
对16QAM-LFM 信号与LFM 信号的模糊函数仿真结果进行对比。16QAM-LFM 信号的模糊图为图钉形状,LFM 信号的模糊图为刀刃形状。通过观察16QAM-LFM 信号模糊图的等高线图发现,16QAM-LFM 信号模糊图只在原点处有明显主瓣,而旁瓣较少;LFM 信号的模糊图能量则集中在一条斜线上。显然16QAM-LFM 比LFM 信号具有更高的时延和多普勒分辨能力。

图6 LFM 信号模糊图的等高线图
4.2.2 虚警概率检测概率仿真
在噪声功率为定值的条件下,改变门限电压值,对虚警概率进行仿真,仿真结果如图7 所示,其中时间长度为30 个脉冲周期。

图7 虚警概率
由式(29)可知,在噪声功率为定值的情况下,虚警概率只与门限电压有关,门限值越高,虚警概率越小。虚警概率的理论值如图7 中实线所示,虚警概率的仿真值如图7 中所示。理论值与仿真值基本拟合,说明了式(29)的正确性。
本文分别在虚警概率Pfa=10-2、10-3、10-4的条件下,对16QAM-LFM 信号的30 个脉冲周期的检测概率进行仿真,仿真结果如图8 所示。

图8 检测概率
由式(35)结论可知,当信号能量相同时,LFM信号与16QAM-LFM 信号具有相同的检测概率,如图8 中连续曲线所示。16QAM-LFM 信号实际的检测概率仿真值如图8 中离散标记符所示。显然,实际仿真值与理论值基本拟合,一方面说明16QAM-LFM 信号的检测概率推导结论式(35)是正确的,另一方面也说明16QAM-LFM 信号的检测概率与传统LFM 信号的检测概率相同。
在探测目标运动的情况下,由于受目标径向运动的影响,产生了多普勒频移,导致检测概率下降。通过图9 的仿真结果可以看出,当目标在低速运动,即运动速度在360 km/h 以内时,检测概率有一定下降;当目标运动速度变大时,对检测概率的影响逐渐变大。

图9 不同速度目标的检测概率
5 结束语
16QAM-LFM 是把LFM 作为16QAM 调制的载波,从而形成新的雷达通信一体化波形。该波形具有良好的通信和雷达性能。相对于现有的雷达通信一体化波形,16QAM-LFM 的通信频谱利用率比低阶调制一体化波形显著提高,运算复杂度又比OFDM-LFM 低。
