平滑改进A*算法在无人机航迹规划中的应用

储泽楠 赵凯 宋倍倍

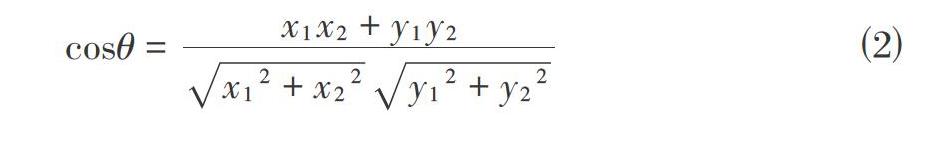
摘  要： 传统的A*算法易于陷入局部极小，搜索速度较慢，规划的路径有较多折线。文章对传统A*算法进行了两个改进，并将其应用于无人机航迹规划。一是在代价函数中加入无人机的转向代价估计，稳定其飞行方向;二是采用后处理方法对航迹点进行拟合，获得平滑的最短路径曲线。为保证拟合后的路径不会出现较大波动，拟合过程没有使用所有的航迹点，而是在一定的误差允许范围内选取特征点进行拟合。改进算法的有效性通过仿真和实验予以验证。

关键词： A*算法; 曲线拟合; 无人机; 后处理

中图分类号：TP399          文献标识码：A    文章编号：1006-8228（2020）02-54-04

Application of smooth improved A-star algorithm in UAV flight path planning

Chu Zenan1， Zhao Kai1， Song Beibei2

（1.Anyang Institute of Technology， 2.Anyang Quality and Technical Supervision， Inspection and Testing Center， Anyang， Henan 455000， China）

Abstract： Traditional A-star algorithm spends much time on searching optimal solution， and is easy to fall into local minima. Moreover， the planned path contains many polygonal lines. In this paper， two improvements are made to the traditional A-star algorithm， and it is applied to the path planning of UAV. One is to add the UAV steering cost estimation to the distance cost function to stabilize its flight direction; the other is to use the post processing method to fit the track points to obtain the smooth shortest path curve. In order to ensure that the fitted path will not fluctuate greatly， the fitting process does not use all the track points， but selects the feature points for fitting within a certain range of allowable error. The effectiveness of the improved algorithm is verified by simulation and experiment.

Key words： A-star algorithm; curve fitting; unmanned aerial vehicle; post processing method

0 引言

A*算法结构简单，易于执行，受到了人们的广泛关注。唐平[1]等使用动态二叉树表示二维空间，对全局路径规划和局部路径规划进行综合考虑，设计了移动机器人在复杂环境下对动态障碍物进行避障的A*算法。贾庆轩等[2]针对空间机械臂在轨操作任务需求，利用A*算法在空间机械臂的自由工作空间进行无碰撞路径搜索，实现了空间机械臂的避障路径规划。姚远等[3]提出了一种基于稀疏A*搜索算法预规划和改进人工势场相结合的无人机动态避障算法。该算法根据障碍物分布建立栅格化模型，采用稀疏A*搜索算法进行全局航迹规划。王殿军[4]阐述了全局地图构建方法，根据移动机器人的实际运行环境，采用栅格法构建了环境地图，利用A*算法做初步路径规划。文中也指出了A*算法的不足，路径规划数据中包含了所有规划点的坐标，冗余点较多，且移动机器人无法在拐点处调整自身姿态。

针对传统A*算法的不足，很多研究人员提出了改进型的A*算法。针对A*算法时间性能较差的问题，熊壬浩等[5]提出了一种并行搜索和快速插入的算法。改进的算法与原算法相比，大大节省了的搜索时间。Fu等[6]提出了一种改进的A*算法，在进行下一步搜索之前，該算法会直接使用当前规划出的无碰撞局部路径。同时，在算法中引入了后处理模块，通过把局部路径取直的方法提高规划路径的光滑性。

在本文中，针对传统A*算法搜索时间长和容易出现局部冗余点较多的问题，提出了一种平滑改进的实时A*算法。首先对传统的A*算法的代价函数作了改进，加入了转向的代价函数估计。采用后处理的方式对算法规划出的最短航迹进行拟合，拟合后的B样条航迹具有三阶连续导数，能够保证航迹的光滑性，有利于后续的速度规划和飞行控制。最后在二维和三维地图上对提出的方案仿真，基于自制的无人机平台对该方案进行了实验测试。

1 A*算法回顾

A*算法是一种基于栅格的算法。自主运动设备被放置在均匀栅格的地图中。设备需要自行规划路径，从给定的起点到达目标地点。在这个过程中，通常要求路径长度是最短的。而且，规划的路径必须避开地图中的障碍物。为了简单起见，我们对地图环境有如下假设。

假设1：在建立的坐标系中，无人机所处的起始点的坐标是已知的。

假设2：目标地点可以是除去障碍物内的任意位置，坐标是已知的。

假设3：障碍物可以是栅格地图上的任意位置，位置是已知的。

基于以上假设，典型的A*算法要在一个树或图表示的特定搜索空间中，找到最短路径。这条路径是由一系列的节点组成，连接这些节点即可找到最优的路径。首先，A*算法需要将所在的地图划分栅格，有障碍物的栅格用“满”表示，无障碍的栅格用“空”表示。最优路径连接的节点就是某些空的栅格中心。算法需要维护Openlist和Closelist两张表，分别用来保存待检验的节点和已经检验过的节点。路径是否最短是通过如下代价函数来判断。

[F=G+H] ⑴

其中，[F]为代价函数的值，[G]代表从起点到中间节点代价的估计，[H]代表从中间节点到最终节点的代价的估计。注意，在估计[H]时一般忽略障碍物的影响。通常，[G]是欧拉距离，而[H]是曼哈顿距离。典型的A*算法可以通过如下步骤来描述。

输入：地图，起点，终点，障碍物。

输出：最短路径。

步骤1：将起点移动到Closelist，并将与起点相邻的26个节点加入Openlist中，将起点设置为这26个节点的父節点。

步骤2：遍历整个Openlist，查找出代价函数最小的节点，将该节点移动到Closelist中（此时Openlist中会减少一个节点，而Closelist中会增加一个节点），并将该节点作为当前节点。

步骤3：对当前节点的26个相邻的节点进行检查，并对每个节点完成如下步骤。

① 判断该节点是否为障碍物以及该节点是否已经在Closelist中。如果至少有一项条件满足，则忽略该相邻节点;如果均不满足，转步骤3.2。

② 判断该相邻节点是否在Openlist中。如果不在，则将该相邻节点加入Openlist中，把A节点设置为该相邻节点的父节点，计算该相邻节点的代价函数[F，G]和[H]。如果该节点已经在Openlist中，转③。

③ 检查经由A到该相邻节点是否比其他路径好，用代价函数[G]来衡量，即该相邻节点的[G]值（注意：此时的[G]值是以起始节点作为父节点计算得到的）是否比通过A节点到达更小。如果通过A节点到达是比其他路径好，则将该相邻节点的父节点更改为A节点，并重新计算代价函数的值[F，G]和[H]。如果经由A节点到达该相邻节点不是最好的，则返回步骤2。

步骤4：当步骤2和步骤3执行完毕后已经找到了一个当前节点，符合最小路径的条件，则继续下一个当前节点的寻找。

步骤5：重复步骤2，3，4，直到目标节点被加入Openlist中，说明已经找到了最短路径。此时停止搜索。

除起始节点外，所有曾经或仍然在Openlist中的节点都有一个父节点。通过父节点即可以找到最短路径。注意，如果Openlist为空，则说明没有找到最短路径，搜索失败。

2 改进的A*算法

为了能够加速收敛，我们对代价函数进行修改，在代价函数的基础上增加了方向和转向时间的代价。

假设向量[a=[xa，ya]T]表示父节点与目标节点构成的向量，向量[b=[xb，yb]T]表示父节点的相邻节点与目标节点构成的向量，则两者夹角的余弦表示为：

[cosθ=x1x2+y1y2x12+x22y12+y22] ⑵

式⑵实际上是对方向的估计。另外，在无人机实际运行的过程中，我们总是希望其能够沿直线前进，减少不必要的转向。因此，在代价函数中考虑转向时间的影响是有必要的[7]。转向时间用[K]来表示：

[K=1     转向≥450     其他] ⑶

其中，转向角度总是以角度变化的绝对值衡量。[K]值的引入是为了能够将转向的时间成本计算到代价函数里，以兼顾时间成本。

综上，经过改进的代价函数可以写成：

[F=G+H+Length*（cosθ+K）] ⑷

其中，[Length]表示栅格化地图时使用的栅格的边长（2D）或棱长（3D）。加入[Length]因子是为了能够使所有的代价函数估计能够在同一数量级下。另外，在使用自适应栅格的改进A*算法中，由于[Length]因子的存在，代价函数仍然能够正常的发挥作用。

3 航迹光滑化

尽管A*算法规划出来的路径是最短路径，但是由于栅格化地图的影响，这些路径是以节点的形式存在的。直接连接这些节点构成的最短路径并不光滑，会影响到后续的速度规划和速度控制。为此，Fowler[8]等提出了使用后处理的方法对路径进行光滑化的处理。本文中，借鉴逆向工程里的思想，将A*算法规划的路径拟合为光滑的B样条曲线，方便后续的速度规划和飞行控制。我们改进了基于主点选择的自适应拟合方法[9]，并将其用于拟合A*算法规划出的最短路径。算法的描述如下。

输入：构成最短路径的一系列节点[{N1，N2，…，Nn}]。

输出：光滑的B样条曲线

步骤1：采用局部曲率法计算各节点处的曲率。

步骤2：根据局部曲率寻找曲率极值点作为初始拟合点，这些初始拟合点称为特征点。

步骤3：基于最小二乘法将初始的特征点拟合为初始曲线[α（s）]，其中，[s]为3阶B样条曲线的参数。

步骤4：使用自适应弦长法将所有节点进行参数化。

步骤5：用式计算除选中的特征点外的其他节点偏离初始拟合曲线[α（s）]的距离

[di=α（si）-Ni]   ⑸

步骤6：将最大偏离距离对应的节点加入到初始拟合点，并重复步骤3-5，直到满足如下条件：

[j=1nα（sj）-Nj≤δ]    ⑹

其中，[δ]为给定的误差上限。光滑后的曲线为3阶的B样条曲线，其具有连续的3阶导数信息，完全能够满足后续速度规划的要求。

4 仿真与实验

本文使用仿真和实验的方法来验证提出算法的有效性。仿真软件使用Matlab，运行在装有win7的PC机上，内存8G，处理器为AMD-6500。总共进行了两组仿真，一组是在二维空间中进行;另一组是在三维空间进行。

测试1：

为了测试本文提出的方法的有效性，测试1在30m×30m栅格地图上进行。如图1（a）所示，其中黑点表示障碍物，蓝色加号表示改进A*算法规划出的航迹点。其中，绿色圆圈表示起始点，红色圆圈表示目标地点。从图中可以看出，这些航迹点能够避开障碍物，但是由于栅格化地图的缘故，得到的航迹点是节点不是曲线。用线段连接这些航迹点可以得到最简单的航迹，然而光滑性很不好。采用我们提出的B样条拟合的方法对航迹点拟合可以得到光滑的航迹，如圖1（b）所示。

测试2：

二维环境下没有考虑无人机在[Z]轴方向上的运动，但真实的无人机是在三维环境下运动的。测试2即在三维环境下对提出的规划算法进行了验证。该三维地图如图2（a）所示，大小为10m×30m×6m，起点设置为[（0，-4.9，0.2）]，终点设置为[（6.0，18.0，5.1）]。图2（a）中红色方块为障碍物，红色实线为无人运动的轨迹。图2（b）给出了无人机在三个坐标轴方向上的速度曲线。从中可以看出速度曲线均较为光滑，说明我们提出的算法成功地光滑化了无人机的飞行路径。

实验在自制的无人机平台上进行，如图3所示。自制的无人机平台包括无人机机体和遥控器两部分，无人机飞行控制部分采用STM32为核心处理器，配合MPU6050作为飞行姿态传感器，HMC5883L作为电子罗盘，GPS作为定位系统。STM32以72MHz的主控频率能够顺利完成A*算法的实时规划。在飞行过程中，无人机通过飞行姿态传感器和电子罗盘获得姿态数据，通过PD控制器实现无人机的姿态控制。配合GPS定位系统，气压计等，无人机可以实现机体在空中的悬停。在实验中，我们给出起点和目标点的GPS信息，无人机顺利的完成了自主航迹规划，飞行到达目的地。

5 结论

本文对基本的A*算法进行了改进，在代价函数中引入了转向和时间控制。采用B样条拟合的方法对航迹点进行了拟合，该拟合方法能够减少拟合曲线的尖点，最大程度的实现航迹的光滑性。在二维和三维空间中对提出的方案进行了仿真，仿真结果表明，提出的方案能够有效的实现最短路径规划和路径光滑化。三维空间中，在各个坐标轴的速度的仿真曲线表明航迹充分光滑，没有出现突变。实验在自制的无人机平台上运行，也证实了方案的有效性。

参考文献（References）：

[1] 唐平， 杨宜民. 动态二叉树表示环境的A*算法及其在足球机器人路径规划中的实现[J].中国工程科学，2002.4（9）.

[2] 贾庆轩，陈钢，孙汉旭等.基于A*算法的空间机械臂避障路径规划[J].机械工程学报，2010.46（13）：109-115

[3] 姚远，周兴社，张凯龙等.基于稀疏A*搜索和改进人工势场的无人机动态航迹规划[J].控制理论与应用，2010.27（7）：953-959

[4] 王殿君.基于改进A*算法的室内移动机器人路径规划[J]. 清华大学学报：自然科学版，2012.8：1085-1089

[5] 熊壬浩，刘羽.A*算法的改进及并行化[J].计算机应用， 2015.35（7）：1843-1848

[6] Fu B，Chen L，Zhou Y，et al. An improved A* algorithm for the industrial robot path planning with high success rate and short length[J]. Robotics & Autonomous Systems，2018：106.

[7] 刘晨曦. 基于改进A*算法的仿人机器人路径规划研究[D].北京建筑大学，2018.

[8] Fowler L，Rogers J.Bézier Curve Path Planning for Parafoil Terminal Guidance[J]. Journal of Aerospace Information Systems，2014.11：300-315

[9] Park H.，Lee JH.B-spline curve fitting based on adaptive curve refinement using dominant points[J].Computer-Aided Design，2007.39（6）：439-451