径向载荷作用下圆筒稳定性的对比研究

刘 帅*

（武汉工程大学机电工程学院）

0 引言

圆筒失稳问题研究大多集中在外压作用的影响上。例如张璩等[1]表明使用有限元法对膜片进行线性屈曲分析为设计提供指导意见是可行的；翟家海[2]通过实验证明了圆筒在外压作用下的弹性临界屈曲力与初始缺陷大小成反比，初始缺陷越大，其临界压力越小。对外压圆筒进行失稳分析可以得到比较精确的结果，但圆筒因为自重影响在吊装运输等过程中受到较大的轴向力，如果其受力超过极限值，也会导致圆筒产生轴向失稳。因此本文在简化力学建模的基础上，基于Eurocode 3：EN1993-1-6 "Strength and stability of shell structures"标准对轴向载荷下的圆筒稳定性进行分析，采用标准公式求出其特征屈曲载荷，并使用ANSYS 软件对其进行具有初始几何缺陷的几何材料及非线性（GMNIA）的数值模拟分析，将两个结果进行对比研究，证明EN1993-1-3 标准中方法的可行性。

1 计算标准

可用长度参数ω 来表示壳体节段的长度：

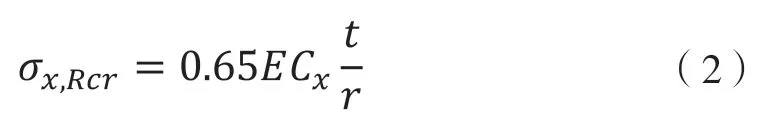
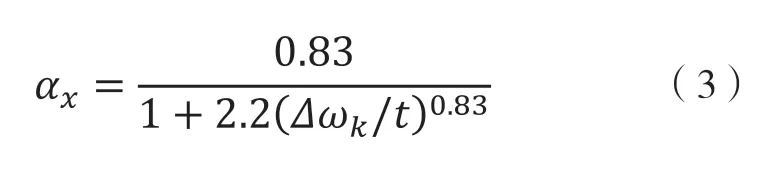
式中：l——圆筒高度；

r——圆筒中径；

t——圆筒壁厚；

E——弹性模量；

Q——径向受压制造质量参数，应根据材料制造等实际情况从表1 中选取。

表1 制造质量公差 Q

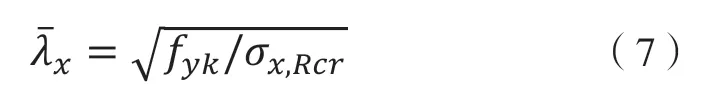
式中：α——弹性缺陷折减系数；

β——塑性范围系数。

设计屈曲应力可根据下式计算得到：

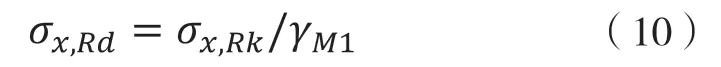
2 GMNIA有限元数值模拟分析

通常设备失稳的理论值与试验值之间存在较大差异。1945 年，Kotter[3]首次提出了“缺陷敏感度”一词，他发现壳体失稳值的差异是由圆筒生产使用过程中产生的几何缺陷造成的。而其中影响最大，反应最敏感的是初始几何缺陷[4]。于是研究者设计了2 种方法来解决这个问题，一种为“一致缺陷模态法”，另一种为傅里叶级数法[5]。本文采用前一种方法进行分析，将特征屈曲的一阶失稳模态乘以相应的比例因子得到的值作为圆筒的初始缺陷值。

（1）建立模型

根据给出的几何参数在SpaceClaim 中建立实体模型并导入Static Structural，添加弹性和弹塑性2 种材料，设置材料的相关参数，然后划分网格，添加约束条件（两端限制移动，转动自由，并允许另一端轴向移动，沿Y 轴负方向施加轴向载荷F=1 N）。

（2）获取静力解

注意使用的是弹性材料，大变形应关闭。

（3）获得特征值屈曲解

在Workbench 界面添加Eigenvalue Buckling 模块进行屈曲分析，求取前三阶的变形量，因为施加的是单位载荷，因此一阶变形的屈曲系数即为弹性临界屈曲载荷。

（4）求出非线性解

为了尽量提高模拟精度，采用“一致缺陷法”求解。根据具体情况给材料添加相应的初始缺陷比例系数，选择相应的弹塑性材料，施加的载荷应略大于所求的弹性临界屈曲载荷值，设置适合的载荷，打开大变形，然后进行求解。

（5）查看结果

按照时间位移曲线图，经换算得到带缺陷的GMNIA 屈曲的临界失稳载荷。

3 结果对比

某个实体模型的壁厚t 为2 mm,材料的弹性模量E 为2×105MPa，泊松比M 为0.3，屈服强度fy为265 MPa，边界条件为顶端BC1f，底端BC2f，A 级公差，r/t 分别为100、80、50、30、10，l/r 分别为10、6、3、1、0.3、0.1 时，按照有限元法和EN 1993-1-6 标准分别进行模拟计算，具体结果可见表2、表3。

表2 EN1993-1-6公式法计算结果 单位：MPa

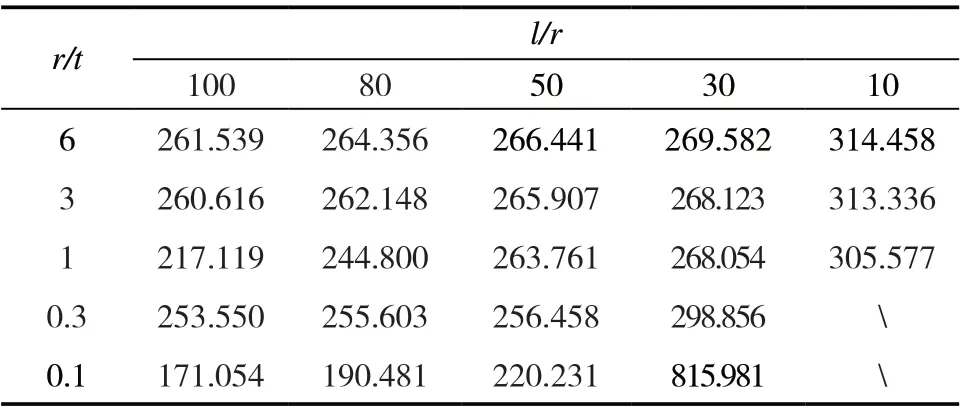
表3 有限元法模拟分析结果 单位：MPa

对结果进行分析后可知，当厚度t 不变时，根据EN 1993-1-6 标准，圆筒的临界屈曲载荷值随着r/t的减小而增大，随着l/r 的增大而减小。通过GMNIA模拟法的结果可知，当厚度t 不变时，圆筒的临界屈曲载荷随着r/t 的减小而增大，随着l/r 的增大而增大。EN 1993-1-6 标准的计算结果相对稳定，有限元法的计算结果则波动较大。结合表2 和表3 可知，当 l/r 小于3 时，这2 种方法的计算结果相差甚远，并且EN1993-1-6 标准的计算结果大于GMNIA 模拟法得到的结果；随着l/r 逐步增大，两者的差距慢慢减小，并趋于稳定。

本次研究的影响因素包含多个方面。一是制造公差质量等级和边界条件，实验证明，采用A 级公差及BC1 和BC2 的固定方式得到的结果明显高于另外两种情况，且与有限元模拟结果最为接近。二是一致缺陷模态法虽然将模型复杂凌乱的缺陷问题简单化、具体化，且便于研究，但得到的结果与实际结果存在较大误差。

4 结论

为了研究轴向受压圆筒的稳定性问题，分别依据EN 1993-1-6 标准进行计算并通过ANSYS workbench软件进行仿真模拟。通过对2 种结果进行对比可知，在一定程度上，两者的结果还是比较吻合的，长圆筒模型计算结果比较接近，中短圆筒模型的计算结果误差则略大。长圆筒模型的公式法计算结果大于模拟值，中短圆筒模型的模拟值则略大于公式计算的理论值。该研究的实际意义在于，在径向载荷作用下，圆筒失稳时的临界屈曲载荷非常大，相较于外压作用下的临界屈曲载荷，其对圆筒所造成的影响比较小，但是在实际设计生产过程中也不容小觑。