基于多模型优选的区域土壤重金属含量空间预测方法研究
2020-04-03黄赵麟王君櫹贾振毅曾菁菁周生路
黄赵麟,丁 懿,王君櫹①,贾振毅,曾菁菁,周生路
(1.南京大学地理与海洋科学学院,江苏 南京 210023;2.同济大学软件学院,上海 201800)
随着城市化和工业化进程的快速发展,土壤重金属的积累越来越明显,重金属污染问题日益严峻[1-5]。2014年《全国土壤污染状况调查公报》显示,我国土壤点位超标率达到16.1%,其中由重金属导致的超标点位数占超标点位总数的82.8%[6],这一调查结果受到社会各界的广泛关注。掌握区域土壤重金属含量的空间信息与变化特征,是实现土壤资源优化利用以及土壤环境保护和防治的重要手段[7]。因此,拓展土壤重金属含量空间预测理论,探索和改进空间预测技术手段,具有重要的科学与现实意义。
近年来,人工神经网络(artificial neural network,ANN)方法开始逐渐应用于土壤重金属污染领域[8]。ANN可通过大量训练方式完成模型构建和变量预测等工作[9-10],特别适合处理多条件、内部机制不明确和物理过程不清晰的非线性问题[11]。国内外学者选取了不同的建模要素,尝试优化提高模型预测精度,获得更准确的重金属空间分布特征。ANAGU等[12]优选了13种土壤属性作为人工神经网络输入数据,对德国9种土壤重金属含量进行预测,发现其预测精度较线性回归模型有较大提高;胡大伟等[13]、张红等[14]选取经纬度作为人工神经网络建模要素,预测重金属污染空间分布特征;郭云开等[15]以高光谱影像中一阶微分光谱数据作为输入部分,预测了长沙县重金属Cu含量的空间分布特征。目前研究多采用样点地理坐标、土壤属性或人类活动等单一因子作为利用神经网络方法预测土壤重金属含量的建模因素,并且多将单一预测模型应用于多元素与研究区全境,忽略了空间区域和重金属元素间的差异性,缺少对模型适宜性的对比与优选研究,这大大削弱了该方法在土壤重金属污染风险预测、管控和治理等方面的有效性。
基于GIS技术和反向传播网络(back-propagation network,简称BP神经网络),将影响土壤重金属分布的“源”因子、土壤属性的“汇”因子以及空间分异因素纳入土壤重金属空间分布预测模型构建中,进一步对比不同模型在区位间、重金属元素间的预测精度,筛选出预测区域重金属空间分布的最优化方案,以期为区域土壤重金属污染评价和管控提供方法和技术支撑。
1 材料与方法
1.1 研究区概况
研究区为常州金坛区(31°33′42″ N~31°53′22″ N,119°17′45″ E~119°44′59″ E),位于江苏省南部地区,面积约为975 km2(图1)。
金坛属北亚热带季风气候区,年平均气温为15.3 ℃,降水量为1 063.6 mm,主要土壤类型为黄棕壤和水稻土。境内地形自西向东逐渐降低,同时该区地处长江三角洲腹地,资源丰富,经济发展迅速,工业发展颇具规模。根据研究区的地形和经济差异特征,将研究区划分为西部丘陵山地区、中部平原城乡区和东部平原农业区3大空间区域。伴随着经济发展的同时,区内土壤也受到了不同程度的重金属污染。
1.2 土壤样品采集及测定
将研究区划分为2 km×2 km网格,每个网格作为1个采样点,对于区域边界上的破碎网格按照四舍五入规则处理,共选取180个样点。按照5点混合采样法采集0~20 cm表层土壤样品,采用四分法取分析样品约1.5 kg。样品经自然风干,剔除石砾和植物残体,研磨后过2 mm孔径筛,充分混匀后用聚乙烯袋保存备用,部分土壤样品进一步研磨后过0.15 mm孔径筛以保存备用。对Cd、Pb、Cr、Cu、Zn元素含量以及pH,有机质(OM)、全碳(TC)、有机碳(Corg)、全氮(TN)、全磷(TP)和全钾(TK)含量进行测试分析。为确保分析的准确性,对空白和标准样品(GBW08303,国家标准物质研究中心)同时进行消解,计算得到回收率为96.7%,满足分析质量控制要求。重金属含量及土壤理化性质测定所用仪器、方法和检验精度按照DD 2005—01《多目标区域地球化学调查规范(1∶250 000)》执行。
1.3 源汇指标的选取与数据来源
在土壤污染研究中,“源”指以人类活动为代表的重金属污染物的来源。选取土地利用方式[16]、交通道路[17]、工业污染源[18]、城市人口密度[19]和水系分布[20-21]作为土壤重金属“源”指标。相对于土壤重金属污染的源,“汇”指可以吸纳重金属的土壤理化性质。由于土壤理化性质对重金属的吸附、迁移和累积能力有较大影响[22-24],故选取pH、OM、TC、Corg、TN、TP和TK作为土壤重金属“汇”指标。其中,土地利用数据、道路交通数据和水系分布来源于江苏省2014年土地变更调查数据。人口密度数据采用中国公里网格人口分布数据集(2010,1 km×1 km)。工业污染源仅包含研究区内国家重点监控污染企业,其基本信息下载自生态环境部网站(http:∥www.mee.gov.cn/)。高程、坡度数据来源于地理空间数据云平台(http:∥www.gscloud.cn/)。
1.4 模型的构建与改进
BP神经网络是神经网络模型中的一种基于误差反传递算法训练的多层前馈网络,它包含神经网络理论中的精华部分,现已成为影响最大、应用最广的机器学习算法之一[10,25]。BP神经网络的模型训练主要分为网络输入信号正向传输和误差信号反向传输2个部分,逐层修正模型连接权值,2个阶段反复交替进行,直到网络输出与期望输出一致为止[26]。
1.4.1模型构建
将基于源-汇因子的模型简称为BP-S模型,将基于空间分异的模型简称为BP-K模型,同时将考虑多种建模因素并加以改进的模型称为BP-SK模型。利用MATLAB R2012a软件中的神经网络构建功能包nntool完成模型构建。模型需要设计的内容包括神经网络层数、输入层节点数、隐含层节点数、输出层节点数、传输函数、训练方法和训练步长等参数。根据影响重金属分布的空间分异与源-汇因素,选取30个指标作为输入层因子(表1)。其中,样点坐标、工业污染源距离、土壤属性因子、人口密度和高程等均以监测值表征,不涉及缓冲区分析。针对土地利用(5种地类)和道路交通,进行500、1 000 和2 000 m 3个半径系列缓冲区分析后共得到18(3×6)个影响因子。
表1 BP神经网络输入因子
Table 1 Input factors of BP neural network

变量因子/单位变量因子/单位变量因子/单位X1500 m缓冲区内农用地面积/hm2X111 000 m缓冲区内水体面积/hm2X21pH值X21 000 m缓冲区内农用地面积/hm2X122 000 m缓冲区内水体面积/hm2X22w(OM)/%X32 000 m缓冲区内农用地面积/hm2X13500 m缓冲区内交通用地面积/hm2X23w(TC)/%X4500 m缓冲区内农村建设用地面积/hm2X141 000 m缓冲区内交通用地面积/hm2X24w(Corg)/%X51 000 m缓冲区内农村建设用地面积/hm2X152 000 m缓冲区内交通用地面积/hm2X25w(TN)/(mg·kg-1)X62 000 m缓冲区内农村建设用地面积/hm2X16500 m缓冲区内道路总长度/kmX26w(TP)/(mg·kg-1)X7500 m缓冲区内城市建设用地面积/hm2X171 000 m缓冲区内道路总长度/kmX27w(TK)/%X81 000 m缓冲区内城市建设用地面积/hm2X182 000 m缓冲区内道路总长度/kmX28高程/mX92 000 m缓冲区内城市建设用地面积/hm2X19到污染企业平均距离/kmX29坡度/(°)X10500 m缓冲区内水体面积/hm2X20人口密度/(万人·km-2)X30样点经纬度坐标
OM为有机质,TC为全碳,Corg为有机碳,TN为全氮,TP为全磷,TK为全钾。
BP-S模型包含所有样点的27个源-汇影响因子(X1~X27),BP-K模型输入层包含所有经过标准化的样点的高程、坡度和经纬度坐标(X28~X30),隐含层通过多次训练选取可使模型决定系数(R2)最大的值,训练方法选用对于中等规模神经网络收敛速度最快的Levenberg-Marquart法,学习步长设置为5.0×10-10,学习步数设置为105,模型达到训练误差目标值后自动停止训练,上述模型均需通过有效性检查(validation check)。使用采三留一验证法对模型精度进行评估[27],将180个样点随机分为建模点位(135个)和验证点位(45个)2个部分。
1.4.2模型改进
BP-K模型仅考虑空间分异和自相关性,忽视人类活动和土壤自身属性,而BP-S模型缺少对经纬度坐标、高程和坡度的考虑,重金属空间分布预测精度可能偏低。因此,根据BP-K和BP-S模型进行综合考量,构建基于源、汇和空间分异多种考量因素下的BP-SK模型。考虑到将30个因子作为变量直接构建综合模型,可能产生共线性问题,且难以揭示变量之间的重要程度,故采用逐步拟合方法对模型进行改进。建模主要过程是首先构建BP-S模型,然后以BP-S模型模拟出的模拟值与真实值之间的残差为因变量,以经纬度为自变量,再次运用BP神经网络建模,利用残差的空间自相关性对原模型进行修正。模型改进具体过程如下:
(1)输入源、汇影响因子数据及建模点位重金属含量,构建BP-S模型。
(2)获得BP-S模型在各建模点位上的模拟值,对比BP-S模型模拟值与建模点位实测值,得到各验证点位上的残差值Δy。
(3)将残差值Δy与建模点位的经纬度进行匹配并对数据进行标准化。
(4)以Δy为因变量,以建模点位经纬度为自变量,构建模拟残差分布的BP-Δ神经网络模型。
(5)输入经纬度数据,获得BP-Δ模型在各建模点位上的残差模拟值以及在各验证点位上的残差预测值。
(6)将BP-S模型的模拟值与BP-Δ模型对应的残差模拟值相加,得到BP-SK模型模拟值;同理,将BP-S模型的预测值与BP-Δ模型对应的残差模拟值相加,得到BP-SK模型预测值。
1.5 模型质量评价与比较
选取R2和赤池信息量(AIC)作为评价模型拟合优度的指标[28]:R2越大,表明拟合优度越高;若改进的模型AIC值减少3个单位以上,则表明模型得到显著改善[29]。此外,选取R2、平均误差(ME)、平均绝对误差(MAE)、均方根误差(RMSE)和相对提高度(RI)作为模型预测精度评价指标。R2越大,ME、MAE和RMSE值越小,模型精度则越高;用RI相对百分比表示2个模型预测精度的差异。
2 结果与分析
2.1 研究区土壤重金属含量及理化性质描述性统计与分析
研究区180个样点土壤重金属含量与理化性质测定结果的描述性统计结果见表2。
表2 研究区土壤重金属含量及理化性质描述性统计
Table 2 Statistical characteristics for heavy metal concentrations and physical characteristics in the study area

指标平均值±标准差最小值最大值峰度偏度变异系数/%背景值w(Cd)/(mg·kg-1)0.192±0.217 0.081 2.53477.0868.415112.50.09w(Pb)/(mg·kg-1)30.70±28.9720.50422.12140.83711.36687.822.3w(Cr)/(mg·kg-1)78.98±6.5362.50109.562.9790.9228.376.2w(Cu)/(mg·kg-1)26.38±5.4218.2946.802.9790.92220.623.9w(Zn)/(mg·kg-1)69.55±17.3244.52198.1619.4553.11224.965.6pH6.64±0.724.378.160.024-0.31110.8—w(OM)/%2.20±0.551.263.550.3400.25824.9—w(TC)/%1.38±0.320.792.170.1010.22422.70.76w(Corg)/%1.28±0.320.742.06-0.0160.13224.90.27w(TN)/(mg·kg-1)1 393±3147952 2370.3360.03122.6460w(TP)/(mg·kg-1)667±1873361 1572.4401.10528.0525w(TK)/%1.57±0.151.492.36-0.684-0.1650.11.86
OM为有机质,TC为全碳,Corg为有机碳,TN为全氮,TP为全磷,TK为全钾。
表2显示,5种重金属含量普遍超过江苏省土壤背景值[30],Cd、Pb、Cr、Cu和Zn平均含量分别为土壤背景值的2.13、1.38、1.04、1.10和1.06倍,表明研究区土壤可能受到不同程度的污染。变异系数(CV)可以反映数据的离散程度,CV越大,说明受人类活动干扰越强烈[31]。5种重金属CV由大到小依次为Cd、Pb、Zn、Cu和Cr,其中Cd和Pb的CV分别为112.5%和87.8%,属于高度变异(>36%),说明这2种元素受外界干扰较大;Zn和Cu的CV分别为24.9%和20.6%,属于中度变异程度(16% 由训练完毕的BP-S、BP-K和BP-SK模型分别得到各建模点位的重金属含量模拟值,将模拟值和样点实测值进行对比计算,并将验证点位的经纬度数据输入训练完毕的3种模型,获得验证点位重金属含量预测值,对比预测值与验证点位实测值,获取不同模型对于不同重金属的拟合优度参数与预测精度参数(表3)以及预测值与实测值散点图(略)。 表3 3种模型拟合优度参数与预测精度参数 Table 3 Goodness-of-fit parameters and predictive precision parameters of three models 元素模型 拟合R2AIC预测R2MEMAERMSECdBP-S0.532-714.3540.4500.0150.0380.071BP-K0.683-887.6440.3200.0070.0470.076BP-SK0.665-745.8780.673-0.0270.0490.066PbBP-S0.702360.8110.4361.4903.7496.795BP-K0.535372.2020.422-0.3134.6166.536BP-SK0.665366.2630.1850.7844.9817.733CrBP-S0.748357.2460.4570.7743.6834.740BP-K0.638398.9080.509-0.0973.4304.139BP-SK0.839310.2150.562-1.2983.9234.538CuBP-S0.751259.8810.508-0.9112.5193.407BP-K0.600254.6840.524-0.5672.3603.128BP-SK0.817217.2940.661-0.5251.8932.682ZnBP-S0.784607.6570.698-4.6796.3298.227BP-K0.605585.1250.454-2.0777.0648.622BP-SK0.906466.6290.7581.3984.0656.123 AIC为赤池信息量,ME为平均误差,MAE为平均绝对误差,RMSE为均方根误差。 在拟合效果方面,除Pb外,BP-K模型对其他重金属元素的拟合R2均≥0.6,各重金属的散点图也基本符合散点聚集于1∶1线周围的规律,散点的线性回归方程系数均低于0.6,说明模型对于低值的预测偏高,而对于高值的预测偏低,预测值变化幅度小;除Cd外,BP-S模型对其他重金属元素的拟合R2均高于0.7,2个模型拟合效果均较好。经改进的BP-SK模型模拟值与实测值散点基本集中在1∶1线附近,说明模型拟合误差小,对Cd和Pb的拟合R2大于0.6,对Cr和Cu的拟合R2均大于0.8,而对Zn的拟合R2则达到0.906,且BP-SK模型中Cr、Cu和Zn的AIC值较BP-K、BP-S模型均减少3个单位以上,因此,BP-SK模型对Cr、Cu和Zn的拟合优度明显高于其他2个模型。 综合各模型的预测精度参数(表3),以R2为判定模型预测精度的主要参数,同时考虑不同模型间ME、MAE和RMSE的差异。在对Cd的预测中,各模型的预测结果差异较大,BP-SK模型预测精度最高,R2达到0.673,BP-S模型次之,R2为0.450,而BP-K模型最低,R2为0.320;在对Pb的预测中,各模型预测结果差异适中,BP-S模型预测精度最高,R2为0.436,而BP-SK模型最低,R2仅为0.185;在对Cr的预测中,各模型预测结果差异较小,BP-SK模型的预测精度最高,BP-K模型次之,BP-S模型最低,R2依次为0.562、0.509和0.457;在对Cu的预测中,各模型预测结果差异较小,BP-SK模型预测精度最高,R2达到0.661,而BP-S模型最低,R2为0.508;在对Zn的预测中,各模型预测结果差异显著,BP-SK模型预测精度最高,R2为0.758,而BP-K模型最低,R2仅为0.454。综上所述,BP-SK模型在预测Cd、Cr、Cu和Zn含量时预测精度较高,其R2比BP-S与BP-K模型分别提高0.223、0.105、0.153、0.060与0.353、0.053、0.137、0.304,而BP-S模型对Pb含量的预测效果较好,其R2比BP-K和BP-SK模型分别高0.014和0.251。 根据研究区的地形和经济差异特征,将研究区划分为西部丘陵山地区、中部平原城乡区和东部平原农业区,得到3种模型在不同空间域的重金属预测精度参数(表4),根据各模型预测精度参数,选取各元素在不同区域的最优模型。在对Cd的预测中,在中部平原城乡区BP-SK模型的MAE值和RMSE值分别为0.045和0.082,MAE值比BP-S和BP-K模型分别降低0.004和0.012,RMSE值则分别降低0.012和0.003;在西部丘陵山地区BP-SK模型MAE和RMSE值分别为0.036和0.057,MAE值比BP-S和BP-K模型分别降低0.017和0.015,RMSE值则分别降低0.012和0.017;而在东部平原农业区,BP-K模型ME、MAE和RMSE值均最低,ME值比BP-S和BP-SK模型分别降低0.006和0.019,MAE值分别降低0.006和0.005,RMSE值则分别降低0.006和0.004。因此,中部平原城乡区和西部丘陵山地区选取预测精度最高的BP-SK模型,东部平原农业区则选取BP-K模型。同理,在对Pb的预测中,东、中部选取预测精度最高的BP-S模型,西部选取BP-K模型;在对Cr的预测中,东、中部选取预测精度最高的BP-SK模型,西部选取BP-K模型;在对Cu的预测中,中、西部选取预测精度最高的BP-K模型,而东部选取BP-SK模型;在对Zn的预测中,中、西部选取预测精度最高的BP-SK模型,而东部选取BP-S模型。 采用ArcGIS 10.2软件生成网格,并通过构建缓冲区、克里格插值等方式获得所有样点的经纬度、高程、坡度以及27个源汇影响因子数据,将公里网格数据分别输入BP-K、BP-S和BP-SK模型并得到各模型在相应点位上的预测值,并通过普通克里格(ordinary Kriging)插值后,得到各模型在研究区全域上的土壤重金属含量空间预测分布(图2)。总体来看,区域中心城镇及东北部的经济开发区土壤Cd、Pb、Cr、Cu和Zn含量均较高,研究区西部丘陵山地区Cd和Pb含量较高,而东部平原农业区Cu含量较高。Cd高值区主要分布在中心城镇与西部丘陵,BP-SK模型对其预测效果较好,但对东部Cd含量的预测精度偏低,而BP-K模型较好地反映了东部Cd含量高值区与低值区的区别;Pb高值区则集中分布在中心城镇地区,BP-S模型能较好地区别Pb在中、东部的高值区与低值区,而BP-K模型在西部丘陵山地区的预测效果最好;在对Cr的预测中,3个模型都出现了类似条带状的分布特征,BP-SK模型在东、中部的预测精度最高,而BP-K模型能够反映Cr在西部丘陵区存在高值;Cu主要分布在城镇中心,BP-K模型预测效果较好,而BP-SK模型更好地划分了东部平原农业区Cu的高值区与低值区;Zn则集中分布在研究区中心城镇与农业区主要交通干道,BP-SK模型对中、西部的预测效果较好,而对东部地区预测效果最好的是BP-S模型。 表4 3种模型对5种重金属的分区预测精度 Table 4 Predictive precision of different zones among three models 元素模型 西部丘陵山地区中部平原城乡区东部平原农业区MEMAERMSEMEMAERMSEMEMAERMSECdBP-S-0.0350.0530.069-0.0090.0490.0940.0110.0310.036BP-K-0.0140.0510.0740.0230.0570.0850.0050.0250.030BP-SK0.0320.0360.057-0.0080.0450.0820.0240.0300.034PbBP-S0.0983.8926.219-2.4186.0848.3402.5772.2942.692BP-K-0.5433.0555.132-0.5675.0618.446-1.3642.8834.126BP-SK0.7414.2517.337-2.1776.6039.377-0.7242.9373.418CrBP-S1.1813.7574.3360.8633.8154.4122.4394.4655.131BP-K0.2063.5434.5870.6234.0474.963-1.2173.1824.537BP-SK0.3604.1495.024-1.3963.4073.860-1.6052.1182.555CuBP-S0.3401.6323.9910.1402.6913.5633.6173.0353.490BP-K0.8531.5563.3230.2762.1362.9963.0354.8805.450BP-SK-0.4141.6993.9520.2202.5013.3610.5491.2471.587ZnBP-S6.1637.1617.8025.0608.41510.5100.6723.8164.639BP-K1.8047.2689.0144.0106.3258.573-1.5924.3435.077BP-SK-2.7134.4187.5120.6463.4904.521-3.2024.6095.969 ME为平均误差,MAE为平均绝对误差,RMSE为均方根误差。 根据各重金属元素在不同区域的最优预测参数(表4),选取RMSE衡量优选前后模型预测精度变化,根据优选前后模型R2验证模型预测精度变化,利用RMSE计算优选组合后模型空间预测精度较原单一模型(即不考虑空间差异的模型)的相对提高度RI(表5),并得到优选后模型预测值与实测值散点图(图3)。优选组合后模型RMSE值通过加权平均东、中、西部最优模型的RMSE值得到,优选前模型RMSE值选用各重金属元素单一最优模型RMSE值。结合表3可知,Cd、Cr、Cu和Zn的单一最优模型是BP-SK,Pb的单一最优模型是BP-S。优选组合后模型对Pb和Cr的整体区域空间预测精度有较大提高,较原单一最优模型分别提高20.71%和19.19%,R2分别提高0.059和0.046,Pb的线性回归方程系数低于0.6,说明对高值区的预测值偏低;对Cd和Zn的整体空间预测精度也有显著提高,精度分别提高15.15%和9.24%,R2分别提高0.028和0.010;Cu的整体空间预测精度提升较小,较原单一最优模型精度仅提高1.75%,R2提高0.026,Cr、Cu和Zn模拟值和实测值基本集中在1∶1线附近,说明离散程度较小(图3)。 图2 优选后土壤重金属含量预测空间分布结果 表5 优选组合前后模型预测精度比较 Table 5 Comparison of predictive precision of model before and after optimization 元素优选后各区域RMSE西部丘陵山地区中部平原城乡区东部平原农业区优选组合后RMSE优选组合前RMSE相对提高度RI/%优选组合后R2优选组合前R2Cd0.0570.0820.0300.0560.06615.150.7010.673Pb5.1328.3402.6925.3886.79520.710.4950.436Cr4.5873.8602.5553.6674.53819.190.6080.562Cu3.3232.9961.5872.6352.6821.750.6870.661Zn7.5124.5214.6395.5576.1239.240.7680.758 RMSE为均方根误差。 为探究重金属元素与源-汇、空间分异之间的影响关系,对研究区重金属含量与30个变量进行双变量分析。在源影响因子中,5种重金属元素与500、1 000和2 000 m缓冲区城市建设用地面积得到的15个相关系数中,大部分存在不同程度的相关性,其中存在极显著相关性(P<0.01)的有8个,存在显著相关性(P<0.05)的有5个,说明5种重金属含量的空间分布与城市建设有较强相关性;Cd、Pb、Cu、Zn和Cr与1 000 m缓冲区内道路总长度间存在显著相关性,Pb、Cr、Cu和Zn与到污染企业平均距离间存在极显著负相关,说明离污染企业越远,重金属受其影响就越小。在汇影响因子中,5种重金属元素与OM、TC、Corg和TN均存在极显著相关性,说明土壤理化性质构成了重金属元素赋存的环境要素,重金属含量高低与土壤汇有着密不可分的关系。如土壤有机质对重金属具有较强的吸附作用,pH环境的改变也可影响重金属在土壤中的富集和迁移[32-33];而所选取的4个空间分异因子在解释Cd、Cr、Cu和Zn含量时,均存在显著相关因子,但在解释Pb时,不存在显著相关因子。相关研究表明Pb含量空间分布主要受到人类活动影响,诸如煤炭燃烧和汽车尾气排放[31,34],工业和交通密集地区Pb含量相对较高[35],“源”因素主导了Pb的空间分布特征。 图3 优选后模型预测值与实测值散点图 针对不同空间区位条件对土壤中多种重金属元素进行差异化、精度最优化空间预测是当前亟待解决的科学问题。笔者研究中,BP-SK模型对东部平原农业区和中部平原城乡区的预测精度整体上高于BP-S和BP-K模型。如在东部平原农业区,BP-SK模型对Cu含量的预测精度最高,通过对重金属元素含量与影响因子的相关性进行分析发现,解释Cu存在显著相关性的源汇和空间分异的指标分别占全部源汇和空间因子指标的66.7%和75.0%;在中部平原城乡区,BP-SK模型对Cd含量的预测精度最高,通过相关性分析发现,解释Cd存在显著相关性的源汇和空间分异的指标分别占全部源汇和空间因子指标的70.4%和50.0%,表明其极大地受到源汇和空间分异双重因素的影响。一方面,这可能是因为东、中部地区工农业发达,受人为因素影响剧烈,从而导致重金属在空间分布中更为复杂;另一方面,重金属元素也受到空间分异的影响,而BP-SK模型恰好综合了影响土壤重金属分布的源汇和空间分异因素,能够有效地解决这种复杂现象下内部机制不明确的空间非线性问题,更好地揭示土壤污染状况。相比之下,在西部丘陵山地区BP-K模型预测效果却更好。如针对西部丘陵山地区的Pb选用预测精度最高的BP-K模型,通过相关性分析可知,Pb与源汇因子呈显著相关的因子数仅为9个,较东部和中部地区分别减少5和12个,但Pb与多数空间分异因子呈显著相关,说明在该地区Pb更多地受到地形影响。究其原因,该地区地势起伏比平原地区大,高程和坡度变化频繁,且丘陵山地区人为干扰较小,更多地表现出重金属含量随自然空间变化而变化的规律,BP-SK和BP-S模型加入过多人为因素反而降低模型对该地区的预测精度,故仅考虑空间分异的BP-K模型能更准确地预测丘陵山地区重金属分布。因此,在今后的研究中,应区分不同空间区域和各元素间的差异,避免模型及其参数选用的盲目性,科学优选出最佳预测模型,可更准确地揭示区域重金属含量空间分布。 但笔者研究仍存在不足,模型所选取的重金属预测参数更多地侧重于土地利用类型的影响,忽略了土壤母质可能对其的影响。另一方面,笔者研究是在区县尺度下进行的重金属含量空间分布预测,并未在其他区域对笔者研究结论进行验证,故在涉及其他研究区域时,笔者研究所得结论有待进一步验证。 (1)BP-SK模型在对Cd、Cr、Cu和Zn含量的空间预测中,其R2较BP-S和BP-K模型分别提高0.223、0.105、0.153、0.060与0.353、0.053、0.137、0.304;在对Pb的空间预测中,BP-S模型的R2比BP-K和BP-SK模型高0.014和0.251。BP-SK模型较其他模型更能突出局部特征,包含的信息更为丰富。 (2)优选组合后模型对Pb和Cr的空间预测精度有较大提高,较原单一最优模型分别提高20.71%和19.19%;对Cd和Zn的预测精度也有显著提高,分别提高15.15%和9.24%;对Cu的预测精度提升较小,较原单一最优模型仅提高1.75%。 (3)不同区域之间同一重金属含量分布规律存在差异,BP-SK模型对人为干扰较大地区的重金属空间分布预测的适用性较好,BP-K模型对自然要素影响较大的丘陵山地区土壤重金属空间分布预测精度较高。2.2 基于不同建模因素的土壤重金属含量预测精度分析与比较
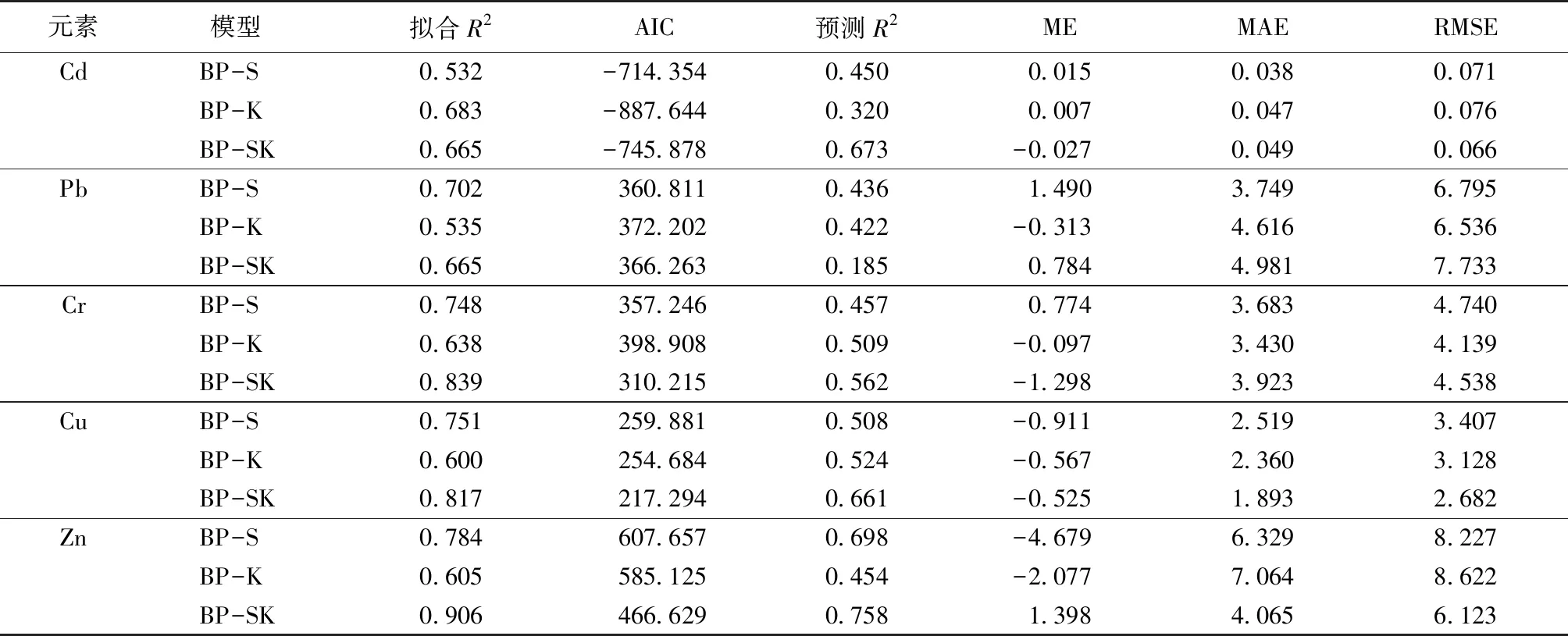
2.3 不同区域土壤重金属模型优选组合
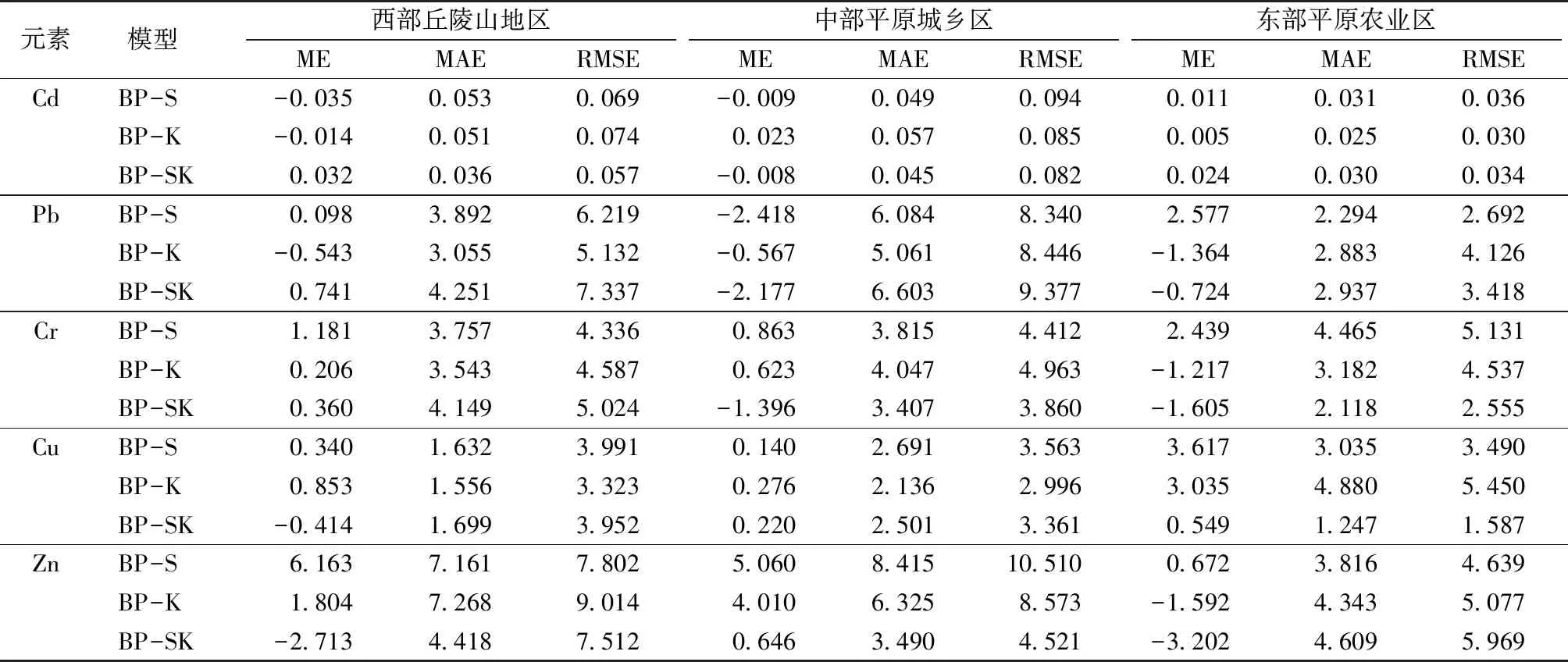
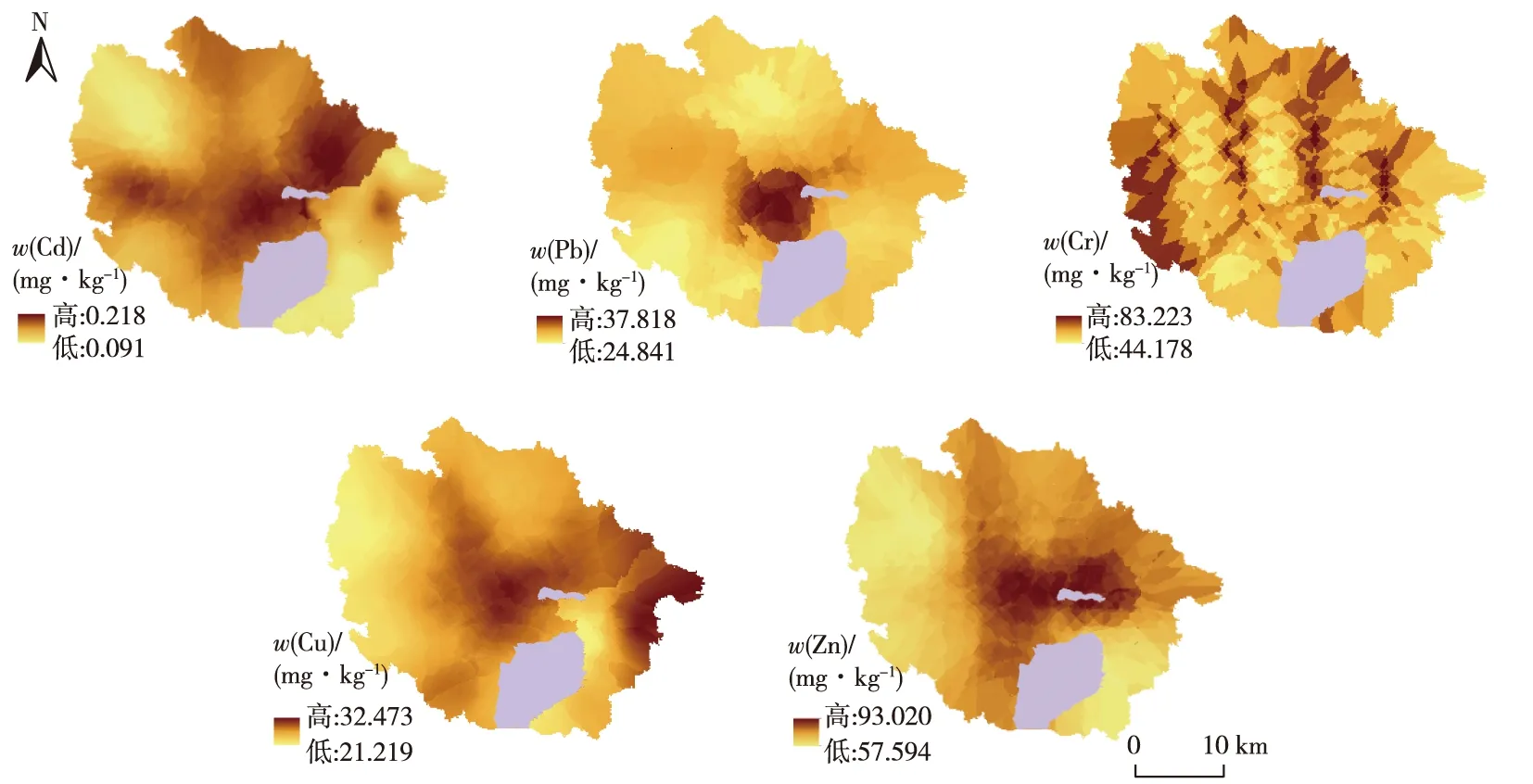

3 讨论
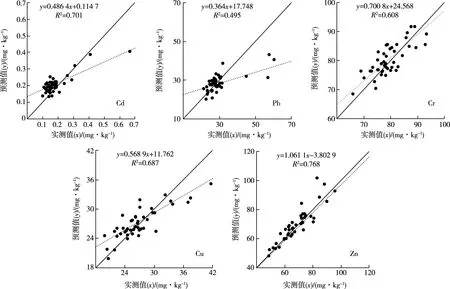
4 结论
