以终为始：支架式教学在小学数学低段解决问题中的实践

孙其英

[摘要]一年级学生的解决问题能力处于发展阶段，因此解决问题能力的培养成为重要目标之一。教学中，教师可通过“问题串”“列举优化”等多种支架在“知道了什么”“怎样解答”“解答正确吗”解决问题三步骤中的运用，让学生对解决问题充满信心，形成解决问题的整体意识，领会数学思想方法，进而形成解决问题的核心能力。

[关键词]小学数学;以终为始;支架式教学;解决问 题

[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068（2020）08-0029-03

一、概念界定

支架式教學在学生已有的知识经验与要达到的目标之间搭建了脚手架，让学生感受到解决问题的乐趣，学会解决问题的方法，提升解决问题的信心，从而获得解决问题的核心能力。

以终为始：以培养解决问题核心能力为终极目标，以终点为起点，追求解决问题教学中学生思维的完整性，从单一片面的碎片化学习走向整体的方法、经验、情感和思想的学习。

支架式教学：基于波利亚的怎样解题理论，为学生在解决问题过程中提供辅助阅读、解题、反思三个步骤的脚手架，便于学生循序渐进解决问题，培养解决问题的核心能力。

二、实践

基于波利亚提出的解决问题四步骤——理解问题、拟定计划、实现计划、回顾与检验，以及人教版教材将小学数学低段解决问题浓缩为“知道了什么”“怎样解答”“解答正确吗”三个步骤，以培养学生解决问题核心能力这个终极目标为起点进行思考和设计各种支架。

（一）支架式教学在“知道了什么”板块中的应用

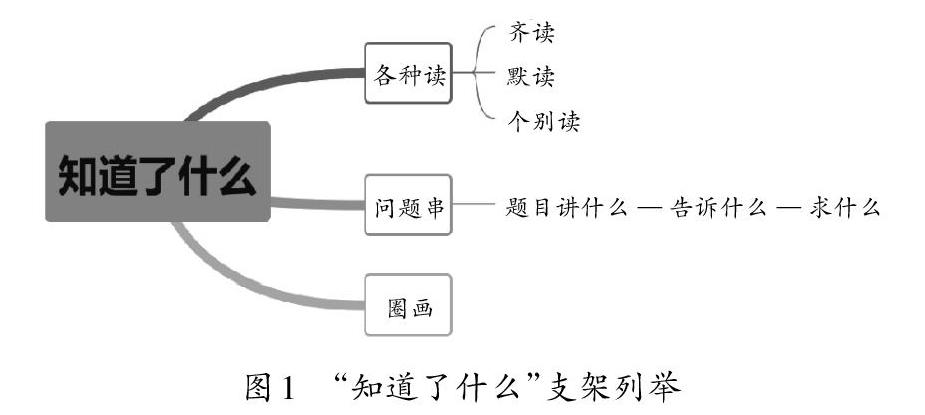
“知道了什么”是对信息进行整体把握，了解已知的条件和要解决的问题。提供各种读、问题串、圈画等教学支架，引导学生将生活情境的描述逐渐抽象到数学理解，将“事理”和“数理”有效链接。

1.采用各种读题方式，理解难懂字词

低段学生识字少，在解决问题时给学生理解和把握信息带来困扰。教师可以采用齐读、默读、个别读等多种读题方式，让学生在读的过程中感悟某些字的意思，也可以让个别学生说说疑难字的意思，从而达到全班领会题目意思的目的。

2.提供问题串，把握整体信息

审题过程中，带着问题去思考，可以为低段学生提供解题台阶，学生拾级而上，整体把握解决问题所需的信息。如图2，教师提出“题目讲了什么事？”“你知道了什么？”“要求什么？”3个问题。学生的回答就很积极：“小朋友们在跳啦啦操。”“知道了男生有9人，女生有6人。”“知道了第一排有7人，第二排有8人。”“要求一共有多少人。”通过对这3个问题的思考，学生厘清了题目的信息，对下一板块“怎样解答”的学习有很大帮助。

3.动手圈画，明确问题关键

在读题的过程中加入动笔圈圈、画画的环节，低段学生会更有兴趣去理解题目的意思。比如：学生圈出两个大圆圈表示已经知道了左边和右边的数量;学生对大括号感兴趣，于是圈出来并提问;在“？只”下面画线，并说出题目问的是一共有多少只兔子。

学生用自己的方式将问题的主干进行了思考和分析，关键的条件和问题就明确了，即“知道了什么”。

（二）支架式教学在“怎样解答”板块中的应用

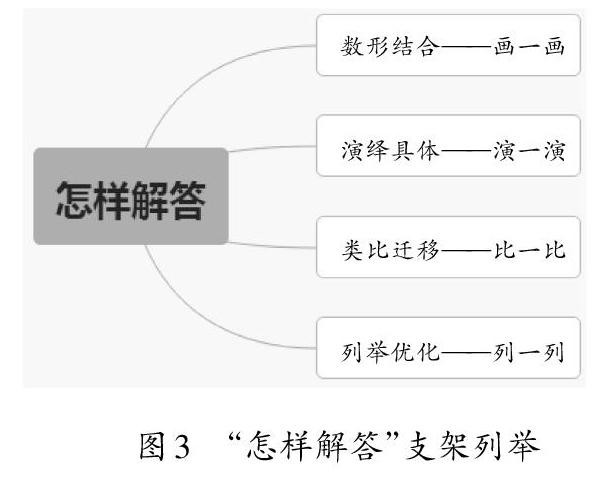
“怎样解答”是解决问题中最重要的环节，教师在引导学生探寻解题思路的同时要进行策略应用能力的培养。

1.数形结合——画一画

学生通过画图，用几何直观来表征题目意思，用数形结合思考数量关系，从而列出正确的算式，这是经常采用的支架教学方法。如图4的例题，教师这样引导。

师：这道题要怎么解呢？

生1：题目中有“还剩”两个字，应该用减法计算。

生2：不对不对，“原来有”的怎么会少呢？

师：那我们就用“画一画”来帮助解题吧。

学生尝试画图（如图5），理解了把“领走”的和“还剩”的合起来就是“原来有”的，应该用加法计算。

2.演绎具体——演一演

有些题目的表述很抽象，低段学生理解起来很困难，如果能将题目用“演一演”方法还原成生活场景，学生理解起来就会容易许多。例如，一年级上册教材第79页的例6，问的是小丽和小宇之间有几人。生，：“15-10=5（人）。”看到个别学生露出怀疑的表情，教师拿出分别写着小丽、小宇名字的头饰，并提议：“我们用‘演一演的方法来帮助理解。”学生根据题目意思排好队，发现小丽和小宇之间只有4人。之后，师生讨论如何列式计算，并把算式中的数据与小演员一一对应，理解算理。

3.类比迁移——比一比

在解决问题中，数量关系是从“数学问题”到“数学方法解决”的桥梁。从一年级开始就要让学生对数量关系有感知、会归纳、会类比。例如，一年级上册教材第97页的例5，问的是跳啦啦操的一共有多少人，学生列出9+6=15（人）和8+7=15（人）两种算式。教师引导思考：“与之前学过的题目比一比，与哪类问题很像？”学生面露难色，于是教师出示之前学的几类问题。学生看出了关联，纷纷发言：“跟小兔子题很像，但今天这道题中出现的不是兔子而是人，站的也不一样，小兔子是前后站的。”“今天学的这道题还分男女生。”“这两道题都是将两个数量合起来。”教师总结：“比一比，就会发现类似的题目之前就学过，只是数字和观察角度变了，但都可以根据‘部分数+部分数=总数来解题。

4.列举优化——列一列

列举法不仅是解题的一种支架，更是训练思维的好方法。如图6的例题，学生有3种解题方法，如图7所示。

生1：我写了3个算式，只有6+7=13（元）符合要求。

生，：我有顺序地列出了6个算式，发现5+8=13（元）也符合。

生3：我先试了5+6=11（元），11<13，说明还不够，如果5不变，6变成8，得数是13;如果6不变，5变成7，得数也是13。

师：生：用了有序列举的方法，生，比生：列得少，也找到正解。这都是“列一列”的方法。

教师通过“列一列”列举优化策略，让学生的思维有理有据。

（三）支架式教学在“解答正确吗”板块中的应用

“解答正确吗”将所得的结果进行檢验，与前面两个板块合成一个完整的解决问题闭环。

1.算一算——再算一遍

我曾经对高段学生做过一次调查：“解决问题过程中，你怎样确认自己的解题过程是对的？”有将近70%的学生认为再读一遍题目，思考一下列式是否正确，然后再计算一遍。对于大部分高段学生而言，这个方法可能不是最好的，但移植到低段学生，采取再算一遍却是一种比较好的检验方法。

2.验一验——结果代入

解答完毕之后，要想检验结果是否正确，可以把结果代入题目情境中。如图9的例题，大部分学生列式16-9=7（人），个别学生列式9+4=13（人）或16-4=12（人）。教师请学生检验哪个算式正确。

生1：检验第二个算式，13+9=22（人），但已知的踢球人数不是22人，列式错误。

生2：检验第三个算式，12+9=21（人），但已知的踢球人数不是21人，列式错误。

生3：检验第一个算式，7+9=16（人），正好是题目已知的踢球人数。

师：将结果代入题目情境，看看是不是符合已知条件，这也是一种检验方法。

3.理一理——回顾过程

课程标准解决问题板块第一学段教学目标中的第四条写道：尝试回顾解决问题的过程。在实践中，教师要引导学生用语言表征的方式表述解题过程，整理自己的解题经历，注重回顾方法和经验。如图10，教师请学生说一说：“你刚才是怎样解决问题的？”生1：“我先仔细读题，知道了小华套中的个数减去小雪套中的个数就是多套中的个数，然后列式解答。”生2：“我先阅读信息再画图，明确了用减法计算，最后列式解答。”回顾过程是很好的检验方法，学生通过说方法、说过程，强化解题策略，提高了解决问题的能力。

4.想一想一一再次提问

数学家华罗庚多次提到治学方法，指出学习要经过“由薄到厚，再由厚到薄”的过程。在实践中，教师应引导学生对“一道题”再次提问，引出“一类题”，思考题目之间的共性，建构数学模型。

三、成效

实践表明，支架式教学在培养学生解决问题核心能力方面确实有一定的成效。这样的教学方式符合孩子的童趣心理和认知特点，使学生对解决问题充满热情和信心，课堂参与度大大提高。同时，学生对解决问题的三个步骤形成了整体意识，在低段就能很好地领会数学思想方法，形成解决问题的核心能力。

思考一直在继续，比如，支架类型还可以再丰富，设计更符合学生个体特点，为学生提供更多的选择性;每一个支架运用的操作细则可以再优化、再具体……我将在实践中不断探索和深化，继续丰富支架式教学方法。

（责编：李琪琦）