Kepler-9b、c的近2:1平运动共振分析∗

陈媛媛 王雪枫 马月华

(1 中国科学院紫金山天文台南京210033)

(2 中国科学院行星科学重点实验室南京210033)

(3 南京大学天文与空间科学学院南京210023)

1 引言

目前, 我们发现的系外行星已多达3823颗, 其中有632个多行星系统1http://exoplanet.eu/catalog/.巨大的样本空间为我们提供了丰富的对比和统计指标, 也为更细化的分类统计奠定了基础.对多行星系统中行星周期比的统计发现[1–2], 无论是考虑相邻行星的周期比还是将系统内不相邻行星的周期比加入一起考虑, 最明显的特征是: 周期比均聚集在略大于3:2和2:1 (右边)处, 而在其紧邻的左边(小于3:2和2:1)有明显空缺.关于此现象的解释有很多.

文献[1]讨论了一对行星在气体盘的耗散作用下进入平运动共振后, 在邻近主星的轨道上受潮汐耗散的影响脱离共振的过程.结论显示, 通过假设这种演化模式, 可以用当前周期比来限制行星的潮汐耗散系数与Love数之比.但同时, 这种机制并不能解释所有近共振行星对的周期比.文献[3]指出考虑行星与气体盘之间的引力作用可使相邻行星产生相背迁移, 从而停在任意的周期比, 其周期比的具体值与两行星打开的共同气体空隙中的密度结构有关.文献[4]给出了一阶平运动共振及由一阶共振组成的三体共振中行星受耗散作用影响而产生的半长径及周期比变化的分析表达式, 并提出对周期比已偏离整数比10%的情况, 系统可能依然处在平运动共振中, 只是经历了较强的耗散作用.文献[5]提出了处于共振的两行星周期比本身就有偏向大于整数比方向的不对称分布, 分别用分析和数值方法给出了合理解释.文献[6]通过模拟27个近2:1共振的Kepler系统受潮汐作用远离整数比的过程, 得出在10 Gyr内若要达到现在的周期比所需要的初始偏心率很大, 以致其初始状态不可能稳定, 从而得出推论: 只考虑行星-恒星潮汐并不能解释当前的近2:1 Kepler共振系统.

Kepler-9系统中已发现3个行星, 两个类海王星和一个超级地球, 围绕着一个近太阳质量(1.0±0.1) M⊙的恒星[7–8].其中两个类海王星Kepler-9b和c的周期分别为19 d和39 d, 其周期比接近2:1.其详细轨道根数见表1.表1中m、P、e、i、ω、M0、∆Ω分别表示以地球质量m⊕为单位的行星质量、轨道周期、轨道偏心率、行星轨道面与观测者视向夹角、近点角距、初始平近点角以及两行星轨道的升交点之差.文献[9]讨论了这两个行星在I型迁移作用下到达当前周期比的可能性, 发现模拟结果中的周期比比实际的大很多, 推测是由于其质量较大, 从而有II型迁移的作用.

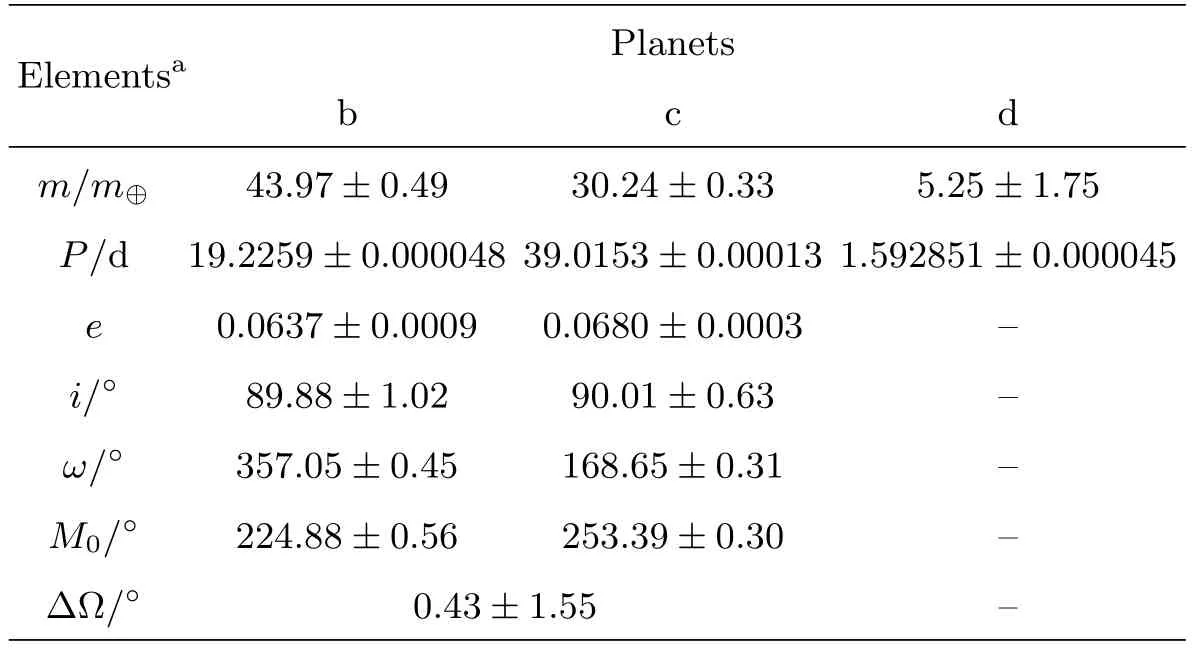
表1 Kepler-9中3颗行星的轨道根数, 其中Kepler-9b、c来自文献[10], Kepler-9d来自http://exoplanet.eu.Table 1 The orbital elements of three planets in the Kepler-9 system.The values of Kepler-9b and c are from Ref.[10], and those of Kepler-9d are from http://exoplanet.eu.

本文利用文献[11–12]中介绍的研究近平运动共振的方法, 对Kepler-9b、c两行星的共振状态进行分析, 并由此讨论了可能的演化历史.第2节介绍了二阶哈密顿分析模型,第3节给出了只考虑长期共振情况下的两个周期解, 同时给出取不同周期解时对应的能量和行星的轨道偏心率.第4节针对Kepler-9b、c的当前各参数进行讨论, 提出此两行星正好处于接近共振区的边缘的观点.第5节是总结.

2 二阶哈密顿分析模型

考虑两个行星围绕一个中心恒星的运动.恒星与两个行星的质量分别为m0、m1和m2, 其中下标0、1、2分别对应恒星、里面和外面的行星(里面的行星对应半长径较短), 这对以下带下标的符号也通用.ai、ei、ϖi、λi分别为两行星的轨道半长径、偏心率、近点经度和平经度, i = 1,2.此工作中基本单位分别为M⊙、au和yr, 于是G=4π2.

假设两行星的轨道周期比接近简单整数比(r+1)/r, 其中r为整数.此时系统的哈密顿函数可以表示为:

其中H0为开普勒部分, Hsec为摄动中的长期项, Hres为摄动中的共振项.H0可以表示为:

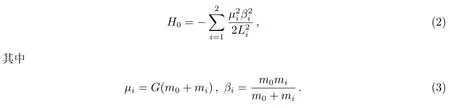
Li=为庞加莱变量,与平经度λi互为共轭变量.另一对共轭变量为Ii=Li−Gi=其中同时, Hsec可以表示为:

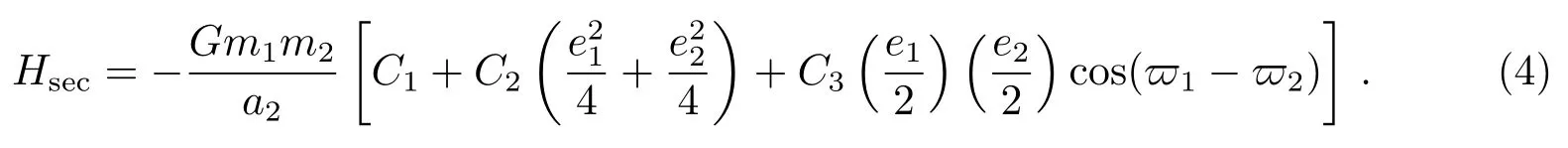
Hres可以表示为:

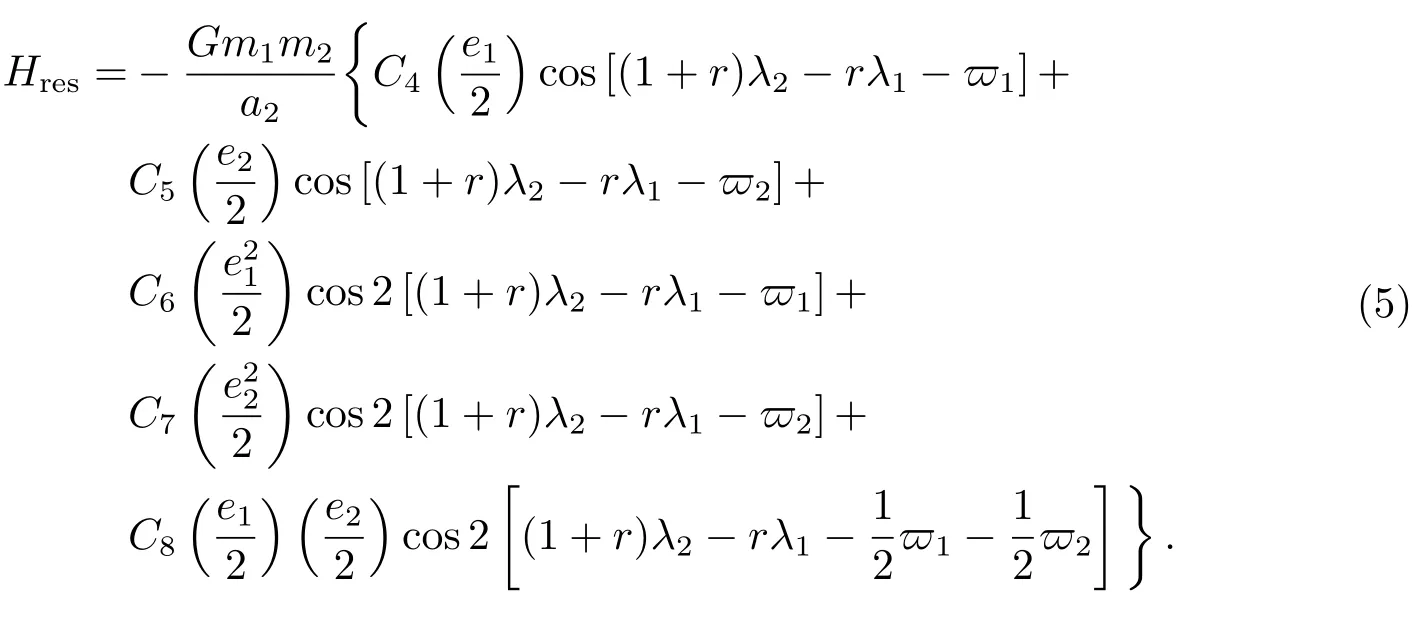
其中系数C1、C2、C3、C4、C5、C6、C7、C8是关于r和半长径之比α = a1/a2的函数, 具体的表达式见附录.而系数C5由于含有摄动函数中的间接项, 因此还是m0、m1和m2的函数.这里的长期项和共振项只截取到偏心率的二阶项, 而舍去了更高阶的项.如果只取到偏心率的一阶项, 则只有一个共振角出现, 可以集中研究一个共振角的平动范围(见文献[13]的第8章).

下一步是通过共轭变换, 把其中的共振角表达式换成一个整体的变量.从旧变量Ii,−ϖi;Li,λi, 到新变量Ii,σi;Ji,λi的转换可以利用下列变换实现:

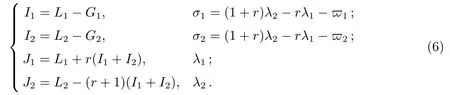
将哈密顿方程中含角度的部分变成其中两个角变量σ1和σ2的函数, 于是另外两个角变量λ1和λ2便不会出现在方程中, 它们的共轭变量J1和J2即为运动常量.因此, 此系统由含4个自由度变成了仅含两个自由度.

变换后的哈密顿方程为:

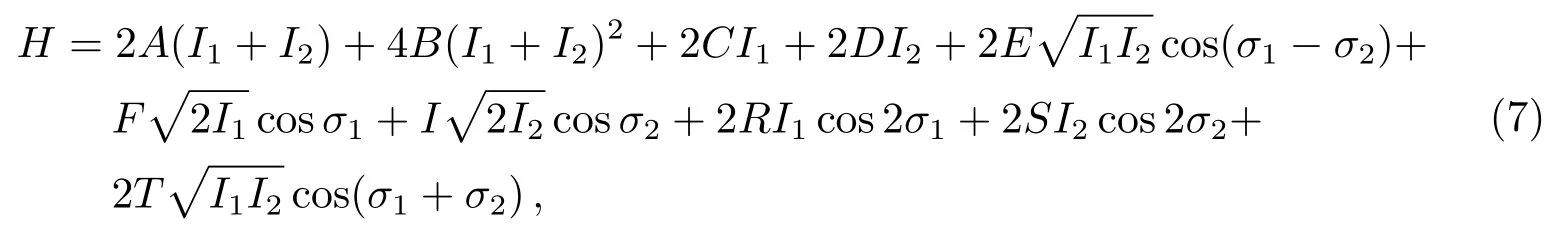
其中系数的具体表达式见附录.前两项来自于哈密顿方程(1)式的开普勒部分H0, 分别为偏心率的二阶和四阶项.含系数C、D、E的3项来自于开普勒部分和长期项Hsec, 为偏心率的二阶项.剩下的项对应共振项Hres, 其中含F、I的两项为一阶主要共振项, 后面3项为二阶项.

进一步进行如下共轭变换:

上述哈密顿方程可以隐去根号和三角函数, 变成更简单的代数形式:

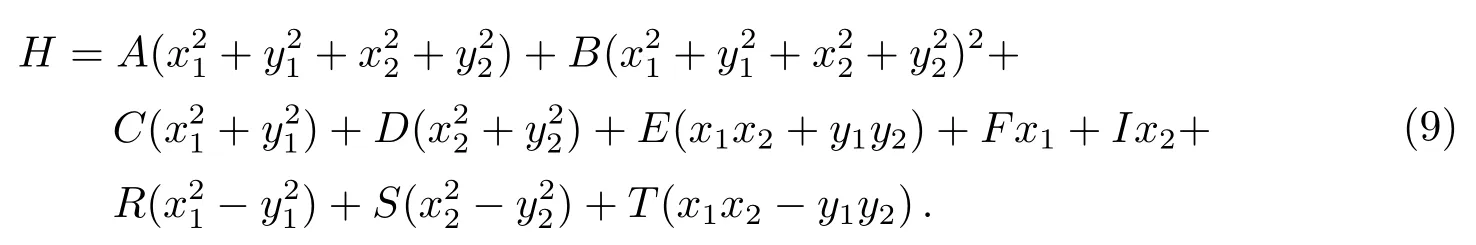
本文我们将考虑σ1平动对应的共振, 于是引入参数

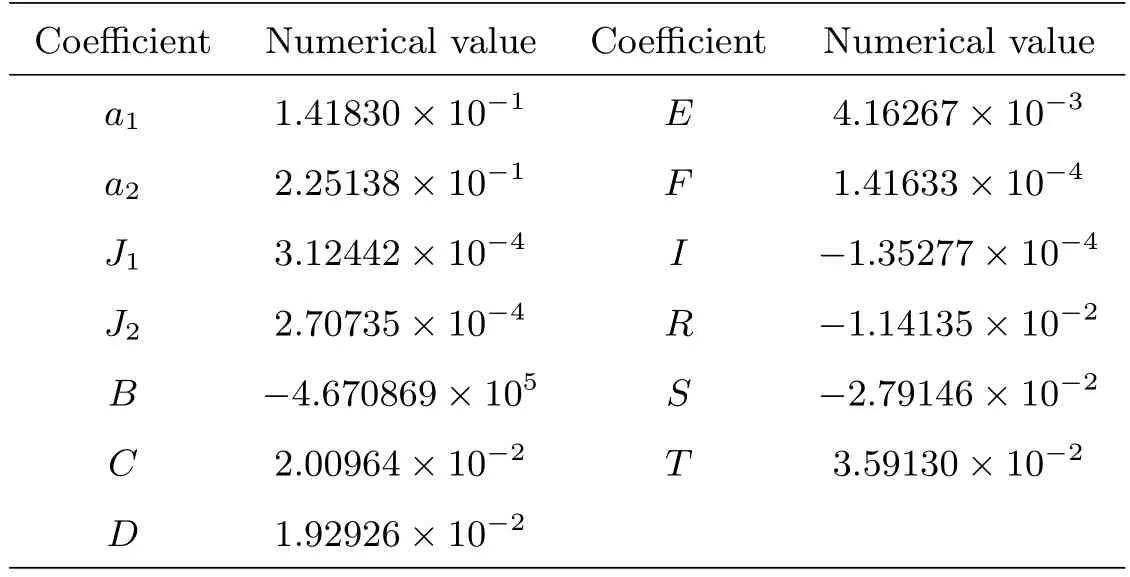
表2 Kepler-9b、c在2:1共振附近各参数取值列表Table 2 List of parameters of Kepler-9b and c near 2:1 resonance

3 长期作用下的哈密顿方程

当系统离共振中心较远时, 各个共振角都处于循环状态, 对系统没有长期影响, 此时可以去掉(7)式中后面5项共振项, 从而简化方程.经简化后的方程只剩一个长期项的角,于是可以做如下正轭变换:

此时哈密顿方程变为

再经过(8)式变换, 上述方程可变为

变换之后的(12)式中不含角变量ϕ, 所以其对应的角动量K2是常量.于是变为一个自由度的哈密顿方程, 是可解的.哈密顿方程如下:

其中K1= 0和K2= K1是方程中的两个奇点, 这对应e1= 0或e2= 0, 即两行星中有一个轨道为圆轨道的情况.两行星之间的引力摄动使得其轨道偏心率不可能始终严格为0,所以对含两行星的动力系统来说, 方程中的奇点情况或许有瞬间会满足, 但并不会对应持续的稳定状态.

设(13)式中的变化率都为0, 从而得到只考虑长期共振时哈密顿方程的周期解, 详细说明见文献[11].首先令=0, 从而得到∆ϖ =0或者∆ϖ =±π.这一关系把周期解分成了两组, 通常把满足∆ϖ =0的这组周期解叫做模态I (Mode I), 而把满足∆ϖ =±π的这组周期解叫做模态II (Mode II).此两种长期作用下的模态在文献[14]中有详细的研究.

将此关系代入(12)式, 可得Hsec相对K1的关系式为

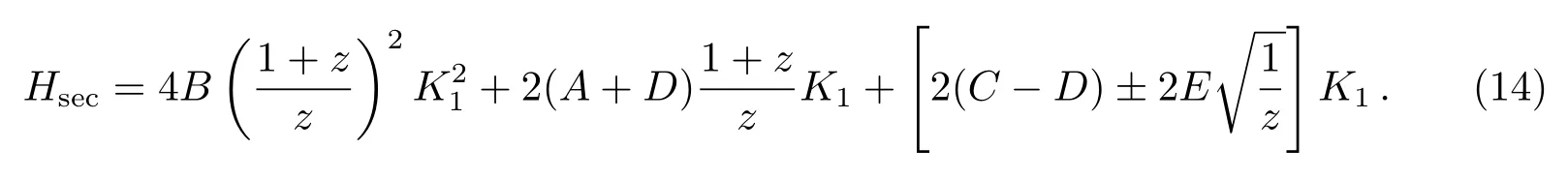
当两行星轨道半长径固定时, K1仅依赖于e1, 而在周期解条件下, e1与e2又是一一对应的关系, 所以由(14)式可得出周期解条件下哈密顿函数随行星偏心率变化的趋势, 见图1.

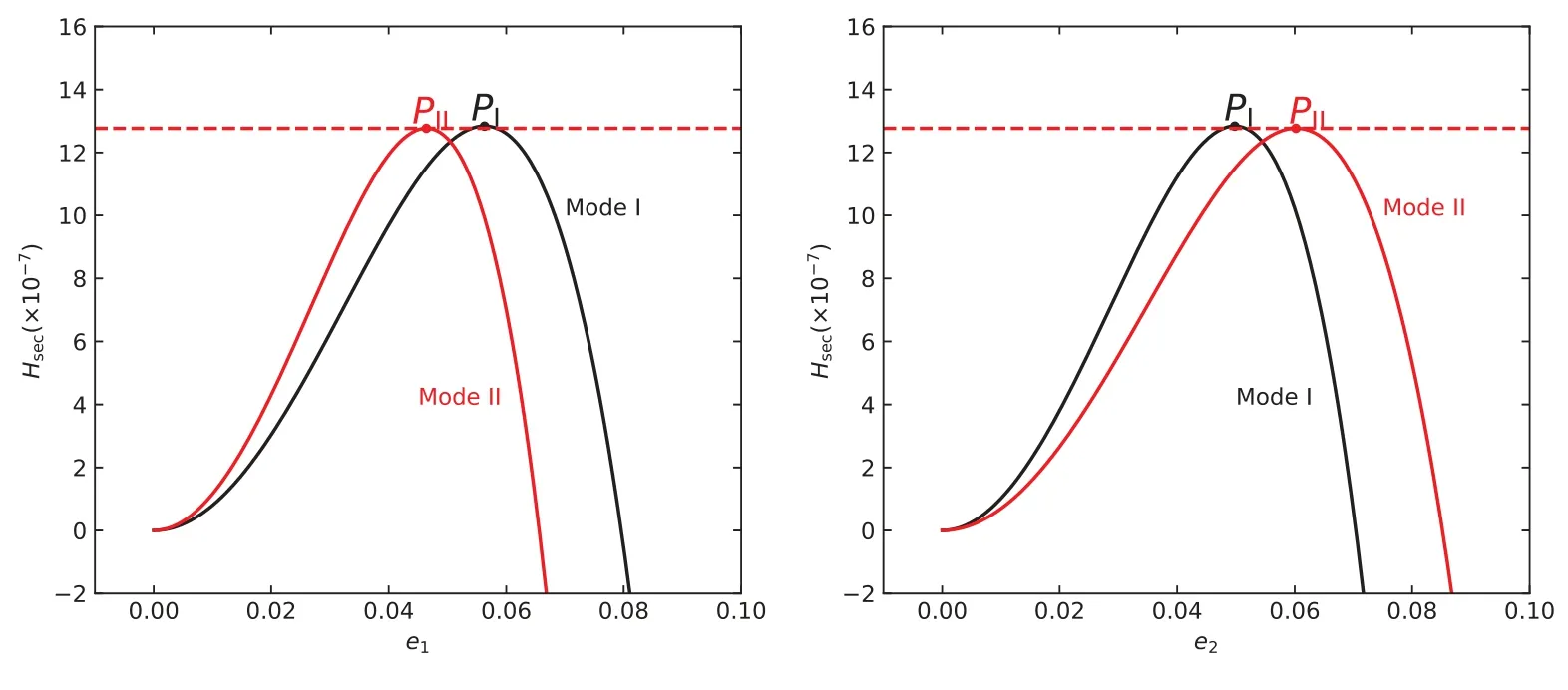
图1 长期作用下的哈密顿能量Hsec随里面行星偏心率(左图)和外面行星偏心率(右图)的变化.黑线和红线分别对应∆ϖ = 0的模态I和∆ϖ = ±π的模态II.两条类抛物线的上面顶点处对应只考虑长期作用时系统的两个平衡点, 模态I中的平衡点PI略高于模态II中的PII.Fig.1 When only considering secular interactions, the Hamiltonian energy Hsec versus the eccentricity of inner planet (left panel) and outer planet (right panel).Black line corresponds to the Mode I with∆ϖ = 0, and red line corresponds to the Mode II with ∆ϖ = ±π, respectively.The vertexes of two parabolic-like curves are two equilibrium points of the system when considering secular interactions only,and the equilibrium point PI in Mode I is slightly higher than PII in Mode II.

图1中两种颜色的线代表长期作用下的两种模态I和II, 黑线为模态I, 红线为模态II.两种模态下的两个最大值均为周期轨道中的平衡点位置.可以看出, 模态II中平衡点对应的哈密顿能量值小于模态I中的最大能量值, 从而在加入共振摄动后先进入不稳定状态[11].

4 能量等高线

下面我们将表示系统离共振中心距离的指标δ固定, 则对应系统能量的哈密顿函数H中含以下4个变量x1、y1、x2、y2或者e1、e2、σ1、σ2.若想画出能量的等高线图,还需要减少两个变量.

由于前面只考虑了长期共振下的周期解满足∆ϖ = 0(mod±π)(mod±π表示将∆ϖ对±π取模), 所以所有初始条件均需使得∆ϖ等于0或±π.同时在平运动共振发生之前, 共振角σ1和σ2是循环的, 其初值可以任意设定, 当然可以设定在0或±π.而当系统处于1:2平运动共振时, 对于对称性稳定平衡解, σ1或σ2均在0或±π附近平动[15].综上所述, 我们固定σ1和σ2在0或±π, 变化e1和e2即可得到系统的能量等高线图, 其中δ =3.0946, 为当前Kepler9-b、c对应的值.

图2是只考虑长期作用下Kepler-9b、c系统当前构型下对应的能量等高线图.图中PI和PII分别对应图1中两个平动模态的能量最大值, 其周围均为稳定区域, 并没有实际的分割线存在.系统当前能量值对应的等高线范围为蓝线部分, 里外两部分对应的∆ϖ进动方向相反.与其相对, 考虑各偏心率二阶项的共振项之后((7)式), 系统的能量等高线图见图3.此时共振区和共振分割线出现.系统当前能量值对应区域接近共振区,在共振区之外, 具体能量值小于共振区的能量值.由此推断, 系统演化过程中可能经历过2:1平运动共振.

由于等高线图中同一根等能量线对应各种不同初值的轨道, 所以为了进一步区分不同初值下各轨道的演化状态, 我们又进一步给出了给定哈密顿能量H和共振距离参数δ后的轨道演化截面图(图4).

首先对哈密顿方程进行积分可得到截面图.对每条轨道, 首先找演化初值.从图3中可以看出, 对于同一能量等高线, 固定e1时对应的e2有4个根或者两个根.在给定条件σ2= π、dy2/dt > 0后, 可限定取最下面的根, 由此可作出里面行星Kepler-9b的截面图.同样, 当固定e2时, 给定条件σ1=0、dy1/dt<0, 可限定取最右边的根, 从而作出外面行星Kepler-9c的截面图.而截面图的判别条件也需要上面对应的限制, 即对于里面行星的截面图, 需同时满足y2= 0、dy2/dt > 0和x2< 0; 同样对于外面行星的截面图, 需同时满足y1=0、dy1/dt<0和x1>0.根据以上条件作出的截面图见图4上面两图中的灰线.两个截面图均有两个中心点, 左边点对应长期作用下的平动模态II, 右边点对应平动模态I.

同时, 为了确定各轨道的状态为稳定还是混沌, 看是否存在分割线, 我们进一步给出里面行星截面图中对应轨道的频谱分析(图4中右下图).对每条轨道中x1随时间的演化序列值作FFT (Fast Fourier Transform)频谱分析, 记录大于最大强度0.01倍的频率作出此图.图中各频率随不同初值连续变化, 表明各轨道均为稳定轨道, 不存在分割线或混沌区.这与图3中所得出的结论一致, 表明系统并没有处在共振区, 其系统能量小于共振区能量.

图2 只考虑长期作用下, Kepler-9b、c系统当前构型下对应的哈密顿能量等高线图.其中δ = 3.0946, 为两行星取当前轨道半长径下所对应的值.图中第1象限对应σ1 = 0、σ2 = 0, 第2象限对应σ1 = π、σ2 = 0, 第3象限对应σ1 = π、σ2 = π, 第4象限对应σ1 = 0、σ2 = π.图中两条蓝线标示了由系统当前观测值计算的能量范围所对应的线性区域.PI和PII分别对应两个平动模态下能量取最大值的位置, 与图1中的PI和PII相对应.Fig.2 The Hamiltonian energy contour of Kepler-9b and c in their current configuration when considering secular interactions only.δ = 3.0946 is the value as the semi-major axes of the two planets are set to be the observed ones.In the first quadrant σ1 = 0,σ2 = 0, in the second quadrant σ1 = π,σ2 = 0, in the third quadrant σ1 = π,σ2 = π, and in the fourth quadrant σ1 = 0,σ2 = π.The two blue lines in the panel indicate two linear regions corresponding to the current energy ranges calculated from the observed elements of the system.PI and PII are the locations where the energies are maximal, in the two libration modes respectively, which correspond to PI and PII in Fig.1.

其次, 为了跟当前观测状态相对比, 我们还给出了用N体模拟结果做的相应截面图.图4中红色圈即对应当前观测值作为演化初值时N体结果的截面轨迹.这一轨迹偏离用哈密顿方程作出的截面图, 可能是由于方程中略去的高阶项引起的.之后我们固定哈密顿能量和表示共振距离的参数δ, 取不同的初始偏心率和相角, 作出了等能量下不同初值的N体截面图, 给出截面图在N体模拟中的整体结构(图4中上两图中的彩线).可以看出,N体结果的截面图虽与哈密顿方程得出的截面图相差很多, 但左右两个中心点也分别对应着长期作用下的两个平动模态, 且每条轨道都是稳定的.

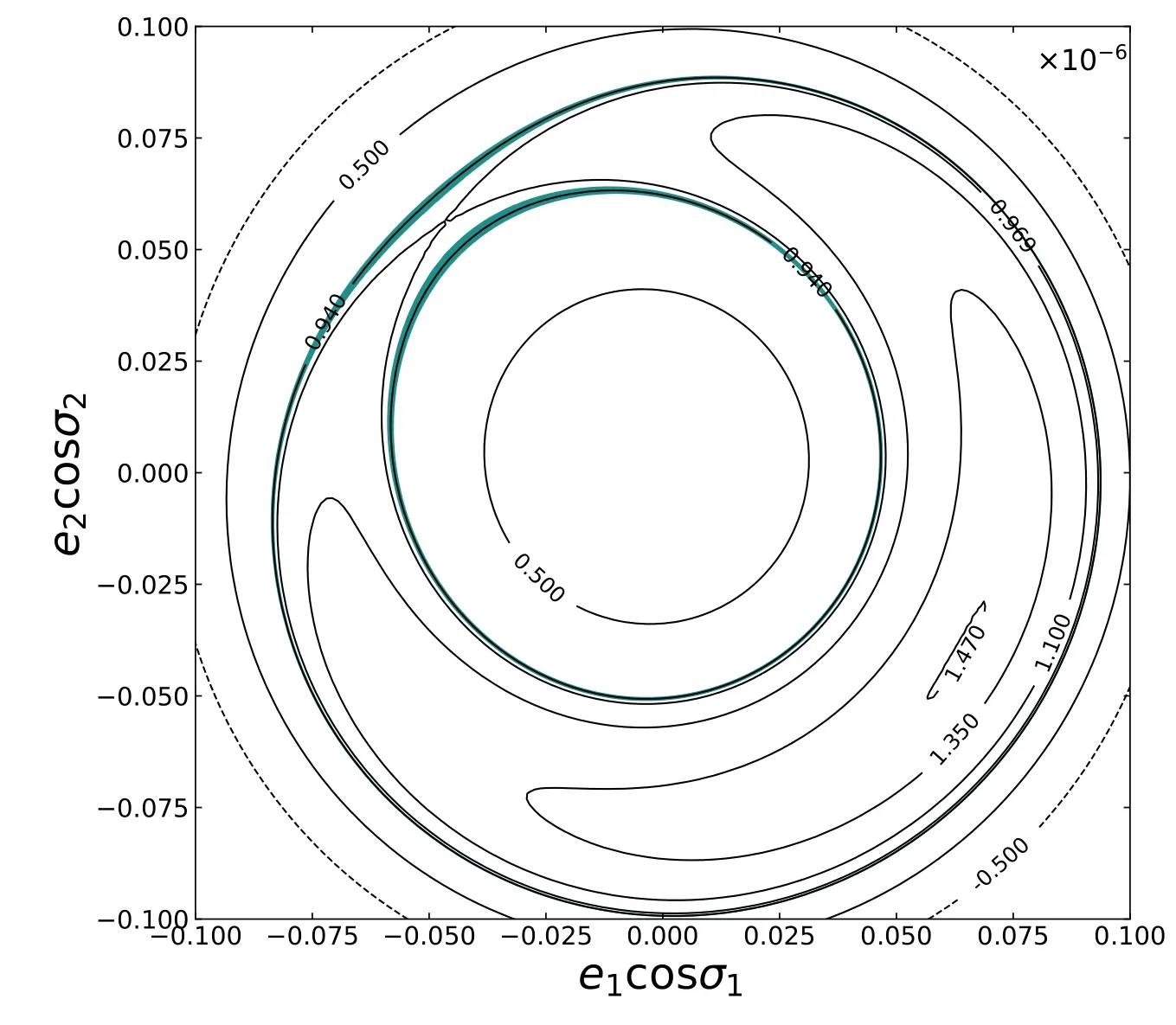
图3 加入所有偏心率二阶项后((7)或(9)式), Kepler-9b、c系统当前构型下对应的哈密顿能量等高线图.图中两条蓝线标示了由系统当前观测值计算的能量范围所对应的线性区域, 香蕉型区域为共振区.可以看出, 当前能量值处于共振区的边缘, 但在共振区之外.Fig.3 The Hamiltonian energy contour of Kepler-9b and c in their current configuration when all terms with the second-order eccentricities (Eq.(7) or (9)) are added in.The two blue lines are two linear regions, corresponding to the current energy ranges calculated from the observed elements of the system.The banana-shaped region is the resonant region.It shows that, the current energy is close to but outside of the resonant region.

5 结论及讨论

本文利用关于偏心率的二阶哈密顿方程, 分析了Kepler-9b、c两行星的共振状态.我们发现, 虽然两行星的周期比为2.03, 但两行星并不处于2:1平运动轨道共振.其系统对应的哈密顿能量略小于共振所需能量, 处于共振区的边缘.此分析方法广泛适用于平面非限制性三体问题中的近共振分析, 也可对已获得较精确观测值的近共振系外行星做统计分析.

以下对Kepler-9b、c可能经历的演化状态做一些讨论.通常认为潮汐耗散会使系统周期比从2:1共振锁定向略大于2方向演化, 但由于这两颗行星中内行星周期大于10 d,它们与恒星之间的潮汐耗散时标远大于系统年龄, 所以可以排除潮汐耗散模型.剩下的可能性有两个: 一是本地形成, 二是受盘的耗散作用从更远处迁移过来.两行星在逐渐靠近的过程中, 周围的气体密度和结构不断变化.受行星-尾迹作用的影响, 在系统经过2:1共振后, 相向运动反弹为相背运动, 而最终停在了当前的位置[3].这一演化模型中行星的最终位置与系统原行星盘中纵深比、粘度系数等各参数之间的相关性还有待进一步研究.

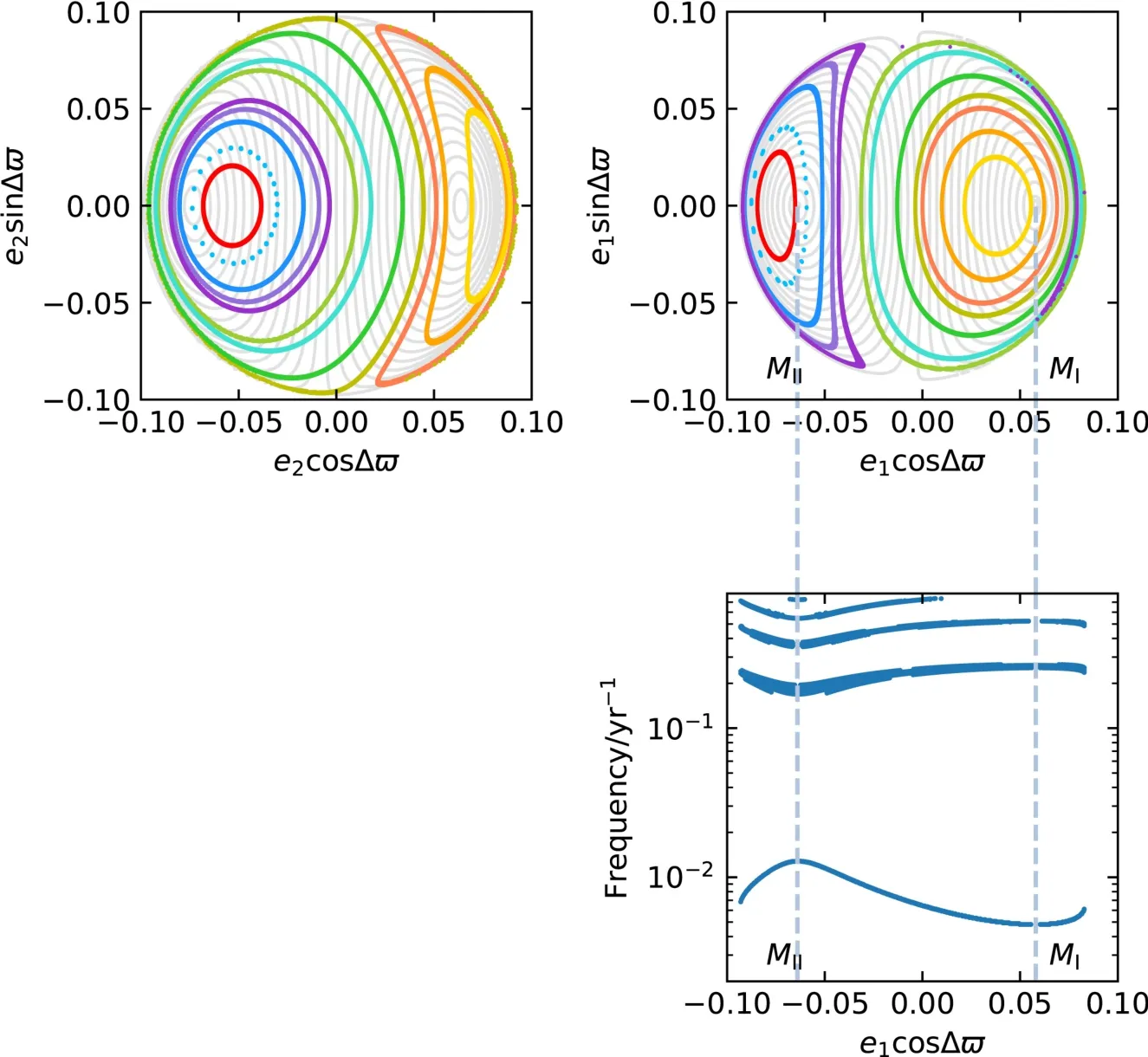
图4 取当前观测值下对应能量H = 9.52×10−7, 对应参数δ = 3.0946, 在不同的初始偏心率和相角下, 对两行星Kepler-9b、c的运动作出的轨道截面图.灰线为积分哈密顿方程得到的截面图, 彩线为N体积分得到的截面图, 其中红线为当前初值下的截面图.右下图为右上图中灰线各轨道对应的x1演化频谱分析图.上两图中左右两边的平衡点位置对应长期作用下的两种平动模态MI (右边)和MII (左边), 其横坐标对应右下图中两条蓝虚线标出的位置.从频谱图中看出,在系统当前能量下所有的轨道都是稳定的, 没有任何分割线或混沌区存在.同时通过与N体的截面图相比较, 可看出哈密顿函数的分析结果存在一定的模型偏差, 此偏差可能来自于分析近似.Fig.4 The cross-sectional view of the orbits of two planets Kepler-9b and c as they evolve with different initial eccentricities and arguments, where H = 9.52 × 10−7,δ = 3.0946, corresponding to the current observed states.The gray lines indicate the cross section obtained from integrating the Hamiltonian functions, while the colored lines from the N-body integrations, and the red one corresponds to that with the current orbital initiations.The lower-right panel displays the spectral maps for x1 evolutions of orbits,and these orbits have been shown by the gray lines in the upper-right panel.The two equilibrium points in the two upper panels correspond to the two libration modes MI (right hand) and MII (left hand) when considering secular interactions only, whose abscissas are consistent with those of the two blue dashed lines in the bottom panel.From the spectral map we can see that all the orbits are stable under current energy of the system, no separatrix or chaotic zone.There are some deviations between the cross section of Hamiltonian and those of N-body simulations, which may be caused by analytical approximations.

致谢感谢耶鲁大学王松虎博士对本文的研究思路提出的宝贵意见.

附录

我们在此给出文中出现参数的具体表达式.在(1)–(5)式中:

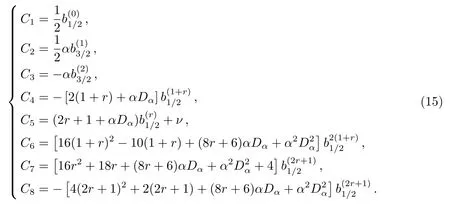
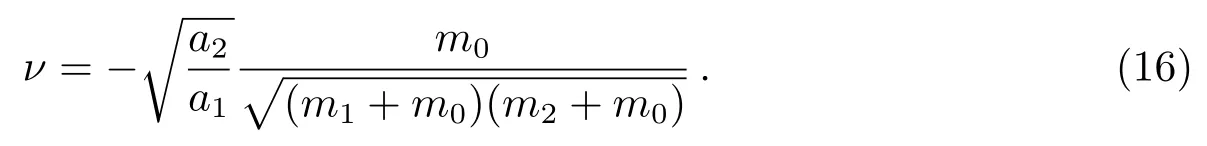
在(7)式中: