基于实时多系统PPP模糊度固定的时间传递算法∗

吕大千 曾芳玲 欧阳晓凤

(国防科技大学电子对抗学院合肥230037)

1 引言

精密单点定位(Precise Point Positioning, PPP)时间传递是一种有效的远距离时间传递方法, 目前PPP时间传递主要用于计算维持国际原子时(Temps Atomique International, TAI)和协调世界时(Coordinated Universal Time, UTC).虽然PPP参数估计所需要的精密产品存在不同程度的时间延迟(例如最终产品需要延迟12–18 d, 而快速产品需要延迟17–41 h), 但精密产品的延迟不会影响对TAI、UTC等时间基准的运行维护, 因此事后模式的PPP时间传递可以满足现有应用场景实际需要.尽管如此, 高精度、低成本且时延更低的远距离时间传递方法对于时间频率研究仍然具有重要研究价值[1].2012年,IGS(International GNSS(Global Navigation Satellite System)Service)组织开展RTS (Real-Time Service)工程, 通过互联网途径播发用于实时PPP的卫星轨道钟差数据, 推动了实时PPP时间传递技术的应用发展.文献[2]采用RTS工程播发的实时数据, 对4个国际时频实验室的时间传递结果进行分析, 结果表明实时模式时间传递结果相对于参考值的均方差为0.3 ns, 时间传递的天稳定度约为2×10−15.文献[3]使用洲际时间传递链路的观测数据进行研究, 发现实时PPP时间传递的标准差可以达到250 ps.文献[4]提出一种实时GNSS时间传递算法, 该方法改进传统PPP观测方程, 通过构建站间单差观测方程, 直接计算测站之间的时间传递结果, 时间传递的标准差小于0.3 ns.作为RTS工程的主要参与者, CNES (Centre National d’Etudes Spatiales)分析中心在整数相位钟差法的事后PPP模糊度固定研究的基础上, 开展PPPWIZARD (Precise Point Positioning with Integer and Zero-difference Ambiguity Resolution Demonstrator)工程,播发用于实时模糊度固定的相位偏差产品, 检验实时PPP模糊度固定性能[5].在时间频率领域, 国际计量局对事后整数相位钟法的时间和频率传递性能进行验证, 而研究基于实时模糊度固定的时间传递技术成为一项亟待开展的重要课题.

随着GPS (Global Positioning System)、GLONASS (GLObal NAvigation Satellite System)、BDS (BeiDou navigation System)和Galileo系统的飞速发展, PPP技术在GNSS以及信号频率的选择上有更多可选方案.自2011年起, IGS组织开展MGEX(Multi-GNSS Experiment)工程跟踪、收集、分析多导航卫星系统信号, 来自多系统的组合观测数据可以显著提升时间传递性能.文献[6]分析了GPS/GLONASS组合PPP时间传递的频间偏差以及系统间偏差对时间传递结果的影响.文献[7]重点研究了频间偏差对GLONASS时间传递的影响, 通过对3种频间偏差估计方案的试验验证, 发现将每颗卫星的频间偏差分别作为估计参数的方案能够最大程度地提升时间传递的性能.文献[8]对GPS、GLONASS、BDS、Galileo的共视法与全视法时间传递进行研究, 结果表明GPS/Galileo组合时间传递性能要优于单系统时间传递.与此同时, PPPWIZARD工程开始播发包括GPS、GLONASS、BDS和Galileo在内的多系统卫星轨道钟差改正数,为研究实时多系统PPP时间传递奠定基础.

本文基于PPPWIZARD工程播发的实时多系统星历、钟差等产品,首先介绍多系统PPP时间传递与模糊度固定原理, 然后检验GPS和Galileo的实时模糊度固定性能, 最后分析多系统观测值和模糊度固定技术为实时PPP时间传递带来的性能提升.

2 多系统PPP时间传递原理

2.1 实时PPP时间传递方法

图1表示实时PPP时间传递方法的原理示意图.在服务端, IGS分析中心接收来自全球观测站的观测数据, 实时估计星历和钟差产品, 并以RTCM (Radio Technical Commission for Maritime service)-SSR (State Space Representation)格式通过互联网播发, 播发数据采用SSR, 实质上是实时星历和钟差产品相对于广播星历和钟差的改正数, 需要恢复成可用于实时PPP计算的轨道和钟差信息.实时星历钟差改正数的网络播发遵循NTRIP (Network Transport of RTCM over the Internet Protocol)协议, 方便用户接收开展实时PPP应用研究.在用户端, 用户以外接时钟作为本地GNSS接收机频率源, 在外接频率源的驱动下, 跟踪、接收导航卫星的伪距和载波相位观测值, 并且接收NTRIP网络服务器播发的实时卫星轨道钟差数据; 然后运用PPP技术计算本地时钟和参考时钟相对于产品基准时间的钟差; 最后计算两地测站之间的时间传递结果, 即计算本地时钟相对于参考时钟的钟差.

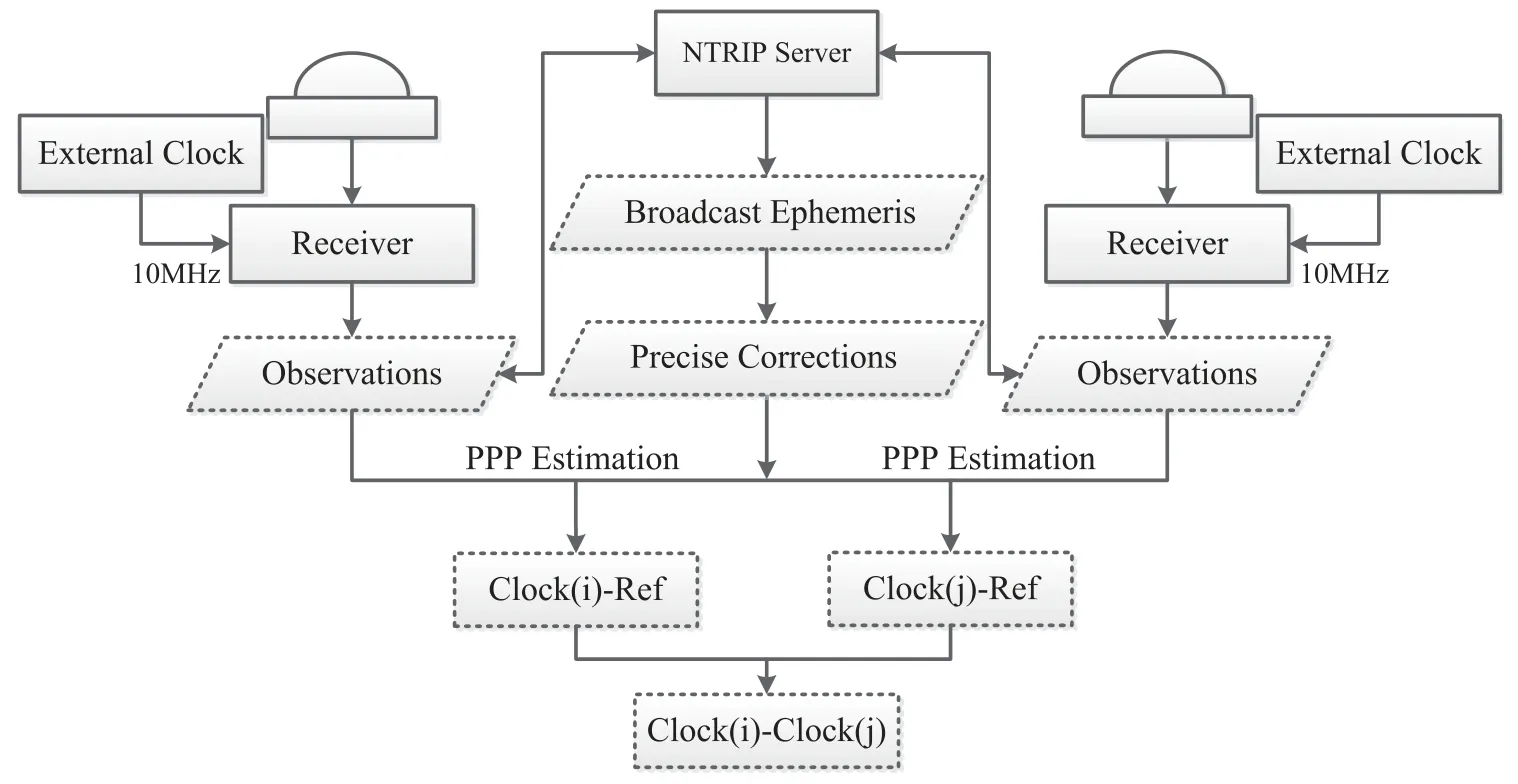
图1 实时PPP时间传递原理.Clock (i): 本地时钟; Clock (j): 参考时钟; Ref: 时间基准.Fig.1 Principle of real-time PPP time transfer.Clock (i): the local clock; Clock (j): the reference clock;Ref: the time reference.

2.2 多系统PPP观测方程

本文采用双频无电离层(Ionosphere-Free, IF)组合观测值进行参数估计, 经天线相位缠绕、相对论效应等误差修正的伪距和载波相位观测方程为[9]:

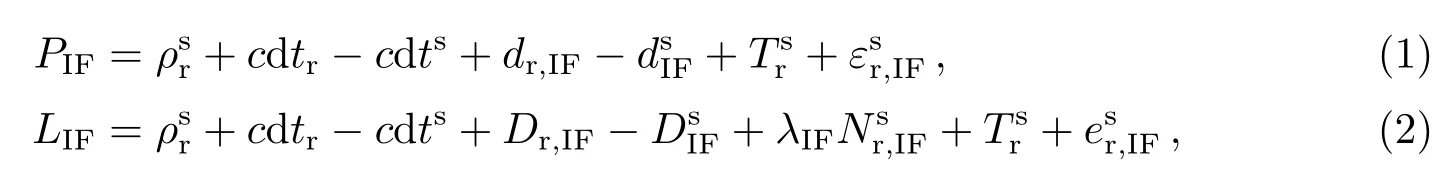
式中, 上标s表示卫星; 下标r表示接收机; 下标IF表示无电离层组合; P和L分别表示伪距和载波相位观测值(单位: m);表示卫星与接收机之间几何距离; c表示真空中的光速; dtr表示接收机钟差(单位: s); d表示伪距硬件延迟(单位: m); D表示载波相位硬件延迟(单位: m); λIF表示无电离层组合的信号波长(单位: m); NIF表示无电离层模糊度参数(单位: cycle);表示天顶方向对流层延迟(单位: m);分别表示伪距和载波相位观测值中的测量误差与多径误差等(单位: m).

通常情况下, IGS组织采用双频无电离层组合的方式估计卫星钟差, 由于卫星钟差和星端硬件延迟线性相关, 两者无法直接分离, 导致卫星钟差产品包含伪距硬件延迟, 使用该类产品进行参数估计会将星端伪距硬件延迟误差引入相位方程, 破坏模糊度整数特性.为解决上述问题, CNES分析中心将伪距和相位方程的钟差区分为包含各自硬件延迟的伪距钟差和相位钟差, CNES通过PPPWIZARD工程播发CLK93伪距钟差产品, 同时还播发相位偏差产品, 用于恢复相位方程钟差的相位钟差特性[10].除相位偏差产品外, PPPWIZARD工程还播发伪距偏差产品用于改正卫星端差分码偏差, 加入偏差产品的PPP观测方程可表示为:

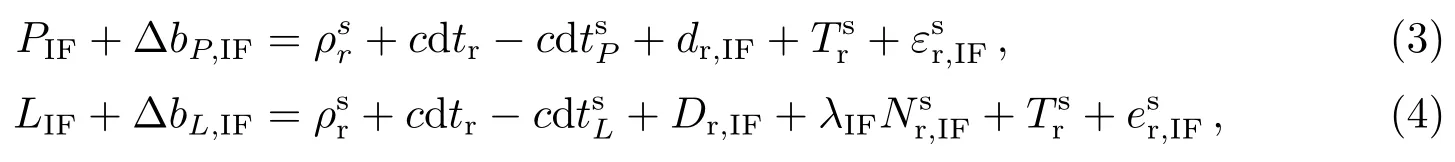
式中, ∆bP,IF和∆bL,IF分别表示无电离层组合形式的伪距偏差和相位偏差产品(单位: m),分别表示包含硬件延迟的伪距钟差和相位钟差, 则实际估计的接收机钟差和模糊度参数同样包含相应的硬件延迟, 即:

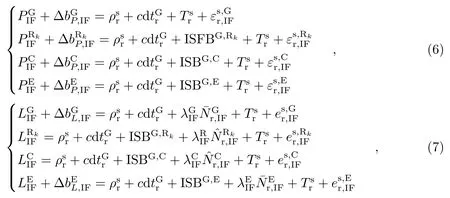
式中, 上标G、C和E分别表示GPS、BDS和Galileo系统; 上标Rk表示编号为k的GLONASS卫星; ISB (Inter-System Bias)表示系统间偏差(单位: m); ISFB (Inter-System and inter-Frequency Bias)表示系统间和频间偏差(单位: m);表示包含接收机端硬件延迟误差的模糊度参数(单位: cycle);表示同时包含接收机端与星端硬件延迟误差的模糊度参数(单位: cycle).对于导航接收机而言, 同一台接收机处理来自不同导航系统信号产生的硬件延迟是不同的, 这种系统间硬件延迟的差异被称为系统间偏差.此外,由于GLONASS卫星采用频分多址(Frequency Division Multiple Access, FDMA)的信号体制, 不同GLONASS卫星的工作频率并不相同, 导致GLONASS信号的硬件延迟存在频间偏差(Inter-Frequency Bias, IFB).本文采用文献[7]提出的方法, 利用模糊度参数吸收GLONASS卫星的相位IFB, 同时对每颗GLONASS卫星的伪距IFB进行单独估计, 则第k颗GLONASS卫星的伪距IFB可表示为:

由于GLONASS、BDS含有卫星与接收机端硬件延迟, 模糊度参数无法固定.相比之下, GPS、Galileo观测值使用相位偏差产品改正, 避免了卫星端硬件延迟被模糊度参数吸收, 本文采用星间单差模糊度固定方法分别固定GPS和Galileo的系统内模糊度.采用Kalman滤波方法进行参数估计, 估计参数包括: 1个接收机钟差参数、1个BDS系统间偏差参数、1个Galileo系统间偏差参数、与GLONASS卫星数量相等的ISFB参数、1个对流层延迟参数以及与观测卫星数量相等的模糊度参数.在随机模型设置方面, 本节使用基于卫星高度角的随机模型决定观测噪声水平; 卫星观测截止高度角设置为7◦;GPS载波相位和伪距观测值的初始标准差设为3 mm和0.3 m, 系统之间观测值权重比根据实时产品质量分析结果决定.

3 星间单差模糊度固定原理

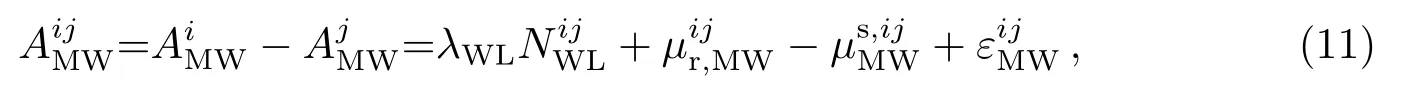
式中, 上标ij表示卫星i与卫星j之间的星间单差操作; NWL表示宽巷模糊度; λWL表示宽巷模糊度波长; µr,MW表示接收机端的宽巷模糊度小数周偏差(单位: m);表示星端宽巷模糊度小数周偏差; εMW表示宽巷观测噪声(单位: m).由于宽巷模糊度波长较长(GPS的L1、L2频段宽巷波长约为0.862 m), 观测噪声以及接收端小数周偏差对模糊度固定影响较小, 经过简单的历元间平滑即可采用直接取整法固定宽巷模糊度.

然后固定窄巷单差模糊度, 窄巷模糊度与无电离层模糊度、宽巷模糊度的关系为:

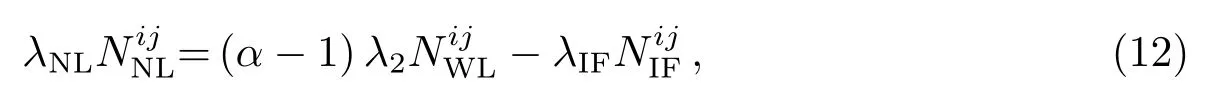
最后固定无电离层单差模糊度.根据已经固定的宽巷模糊度和窄巷模糊度推导得到无电离层模糊度的固定解, 然后以无电离层模糊度固定解为约束条件, 构建虚拟观测方程, 并求解其他参数的固定解:

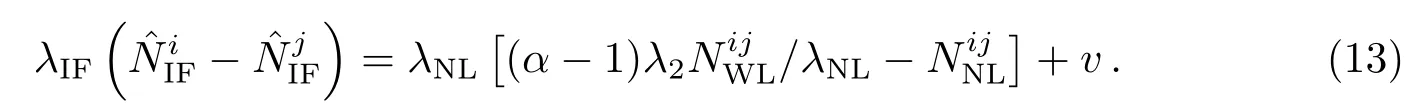
4 实验分析

本文选择3个装备高性能原子钟的IGS观测站, 使用CNES播发的CLK93实时产品进行参数估计, 观测时间为2018年2月16日至3月24日(年积日047–083)共计37 d, 以BRUX站作为中心, 构成BRUX-CEDU和BRUX-STR1时间传递链路, 对实时星历和钟差产品质量、实时模糊度固定和多系统PPP时间传递性能进行研究.

4.1 实时星历和钟差产品质量分析

表1为年积日047–083的实时星历和钟差产品精度统计表, 轨道精度以GFZ (Geo Forschungs Zentrum)最终轨道和实时轨道的均方根误差(Root-Mean-Square, RMS)为评估指标.表中GPS卫星轨道在切向和法向的平均RMS最小, 分别为3.29和2.82 cm,与GFZ最终产品的一致性较好.Galileo卫星轨道的平均RMS值为2.08 cm,略小于GPS卫星, 但是在切向和法向的RMS值较大.对于BDS卫星而言, MEO卫星轨道质量要明显优于IGSO卫星, 但整体来看, 由于CNES在亚太地区BDS实时观测站数量少, BDS实时轨道精度仍然较差.对于钟差产品精度评估, 为避免时间尺度对质量评估造成影响, 本文选择编号为G25、R07、E08和C14的卫星作为各自系统的基准卫星, 首先计算系统内卫星钟差相对于参考星的差值, 然后计算差值结果相对于GFZ差值结果的RMS和标准差(Standard Deviation, STD), 表中钟差评估结果与轨道评估结果基本一致.需要说明的是, 尽管Galileo实时产品与GFZ最终产品一致性较好, 但文献[14]发现, GFZ最终产品的Galileo轨道精度低于GPS轨道, 因此在事后PPP计算中, GPS和Galileo的权重一般设为1: 2.通过星历和钟差质量评估, 本文最终确定实时PPP 4系统(GPS: GLONASS:BDS: Galileo)观测值权重比为1: 2: 3: 2[15], 其中BDS GEO卫星由于轨道钟差精度较差, 相对于BDS MEO和IGSO权重降低为原来的1/10[16–17].

4.2 实时模糊度固定性能分析

本文选取2018年2月16日(年积日047)观测数据, 从模糊度固定成功率与模糊度固定残差分布两方面分析比较GPS与Galileo的模糊度固定性能, 其中模糊度固定成功率采用窄巷模糊度ratio-test检核通过率衡量, 而模糊度固定残差分布情况使用小于0.15周的窄巷模糊度固定残差所占百分比衡量.图2表示模糊度固定成功率示意图, 图中5个测站观测数据的GPS模糊度实时固定率平均为91%, 而Galileo的平均固定率约为70%.图3为窄巷模糊度固定残差分布所占百分比示意图, 表示模糊度固定为整数后的剩余小数周残差分布情况.图中GPS模糊度固定残差小于0.15周的比例要高于Galileo, 表明模糊度固定质量较高, 剩余残差幅度较小.模糊度固定实验结果表明, GPS实时模糊度固定性能要明显优于Galileo, 原因一方面在于GPS的实时产品(卫星轨道、钟差和相位偏差)质量要优于Galileo, 另一方面在于GPS在轨卫星数量要明显多于Galileo.

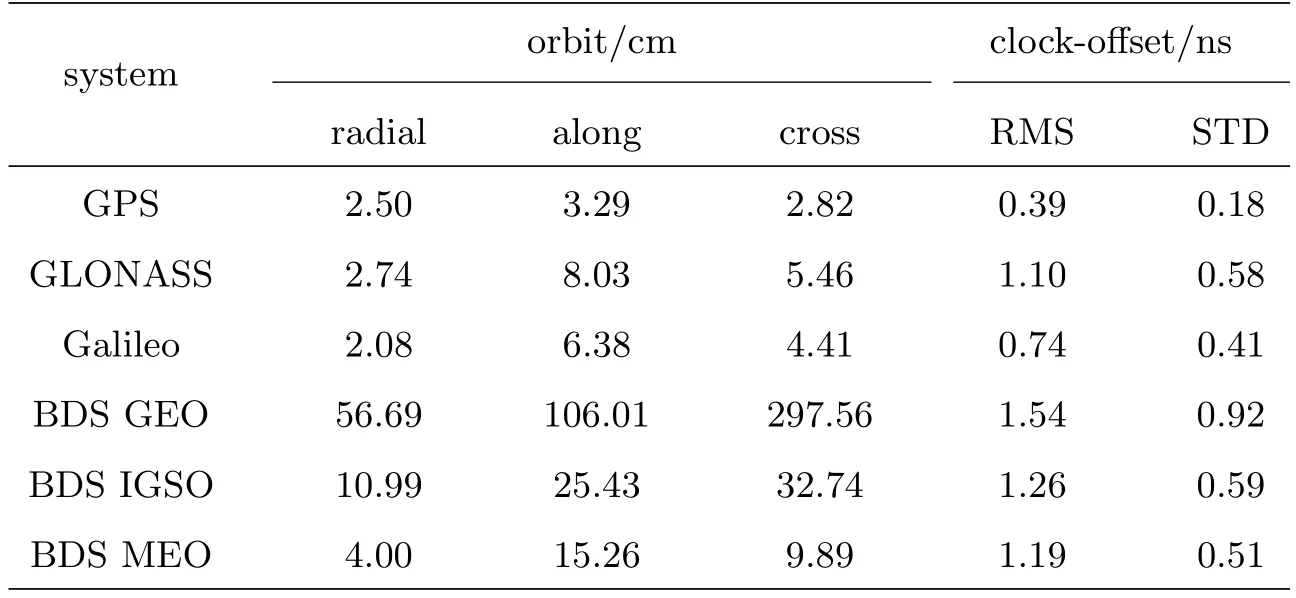
表1 实时星历和钟差产品质量Table 1 Quality of real-time ephemeris and clock-offset products

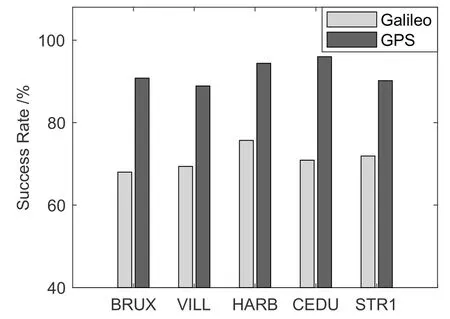
图2 模糊度固定成功率统计图Fig.2 The success rate for ambiguity resolution

4.3 时间传递性能分析

本文验证4种不同PPP模式的工作性能, 检验多系统观测值与模糊度固定对时间传递的性能提升, 详细信息如表2所示.在选择时间传递评估指标时, 本文以基于IGS最终钟差产品的时间传递结果作为参考值, 计算时间传递结果相对于参考值的标准差, 评估PPP时间传递性能.为避免时间传递中的日界效应影响评估结果, 本文首先计算单天时间传递结果的标准差, 然后计算37 d标准差结果的平均值.

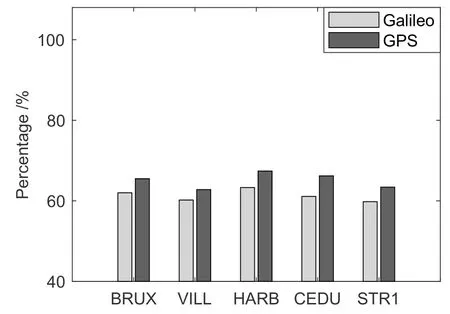
图3 小于0.15周的窄巷模糊度残差所占百分比Fig.3 The percentage of NL ambiguity residuals within 0.15 cycle

表2 不同PPP处理模式的详细信息Table 2 Details of different PPP processing modes

图4为PPP传递结果与IGS参考的差值序列, 此处使用G PPP工作模式作为对照.其中, STR1测站存在共计4 d的观测数据缺失, 并不影响对时间传递的评估.对于相同的时间传递链路, 多种工作模式下的时间传递结果变化趋势基本一致, 其中GRCE PPP AR(G)模式的传递结果与参考值一致性较好, 所有差值序列的标准差结果详见表3.为综合比较上述4种不同工作模式, 图5对时间传递标准差相对于G PPP模式的降幅进行统计.图中GRCE PPP、GRCE PPP AR (G)和GRCE PPP AR (E)模式相比于G PPP的标准差平均降幅分别为7.0%、38.1%和30.9%.通过对图5的比较分析可以得出以下结论:(1)多系统观测值和模糊度固定均可以提升时间传递性能, 但实时模糊度固定带来的性能提升要优于多系统观测值; (2) GPS模糊度固定带来的性能提升要优于Galileo, 主要原因与Galileo实时产品质量以及在轨工作卫星数量有关; (3)综合运用多系统观测值与模糊度固定(尤其是GPS实时模糊度固定)对时间传递带来的性能提升最高.

表3 基于多系统PPP时间传递标准差(单位: ns)Table 3 Standard deviations of multi-GNSS PPP time transfer results (unit: ns)

图4 基于多系统PPP时间传递结果与IGS最终产品的时间差值(DOY: 年积日)Fig.4 Time difference of multi-GNSS PPP time transfer results with respect to the IGS final products(DOY: Day of Year)

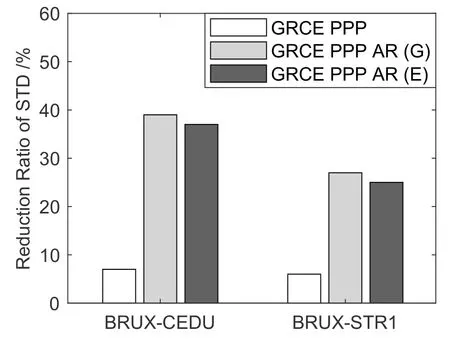
图5 多系统PPP时间传递标准差降幅Fig.5 Reduction ratio of STD values for multi-GNSS PPP time transfer

5 结论

本文使用CNES分析中心播发的实时产品,在综合GPS、GLONASS、BDS和Galileo多系统观测值的基础上进行PPP时间传递研究, 检验了4种不同的PPP工作模式:G PPP、GRCE PPP、GRCE PPP AR (G)和GRCE PPP AR (E), 分析多系统观测值以及实时模糊度固定对时间传递的性能提升.实验结果显示: 实时GPS模糊度固定性能要优于Galileo; GRCE PPP、GRCE PPP AR (G)和GRCE PPP AR (E) 3种模式相对于G PPP模式的时间传递标准差平均降幅为7.0%、38.1%和30.9%; 实验证明模糊度固定能够显著提升实时模式的时间传递性能, 并且综合运用多系统观测值和GPS模糊度固定进行PPP时间传递的性能最优.