数学课堂上的习惯养成与能力提升——以“直角三角形全等的判定”一课教学为例

杨 微

（大连市甘井子区春田中学）

“直角三角形全等的判定”这节课主要讲授直角三角形全等的特殊判定方法，内容看似简约，教学处理却并不简单。结合本节课教学设计、组织教学、学生体验等方面的实施情况和教学效果，我对“以习惯养习惯，以能力提能力”有了全新的认识和思考。

一、让学生在合作与展示中养成学习习惯

（一）学生的合作习惯源于教师的观念与设计

课改理念的关键点之一是转变学生的学习方式，而同伴合作是转变学生课堂学习方式最稳妥、最有效的途径和方法之一。

本节课课始，我设计了一个小组合作探索的活动。即给定两个直角三角形，让学生探究添加两个什么条件可以使他们全等。目的是复习学过的知识，并在此基础上引发新的学习内容，以起到温故知新、承上启下的作用。在探索的过程中，同伴合作的作用明显。当活动指令下达后，学生便开始了他们熟悉的合作研讨。学生在同伴交流中唤醒了记忆，明晰了可以用“SSS”“SAS”“ASA”“AAS”等学过的判定方法使两个直角三角形全等；学生在辨识与争论中补足了认识，明确了可以运用不合理的“边边角”对应相等来判定这两个直角三角形全等。借以“启下”并“知新”。

课堂中的合作学习，需要师生之间“守望相助”。课堂里不乏基础差、底子薄的潜能生，他们是课堂学与教有效性的参照。这就需要教师要有组织合作学习的愿望，能够尊重并接纳学生之间的差异，并把差异变成资源，组建“学习共同体”。教师要经常性地组织有效的合作学习，调动学生参与课堂的积极性，发动学生互帮互助，力求不让一个学生掉队，力争将课堂教学的效益最大化。

人往高处走，潜能生的学习愿望是向好的。但在学习过程中潜能生往往会出现学不会、不会学的状况。如果组织学生合作学习，这种情况就会有所改观。通过牵手合作，让学生之间学力互补、经验共享，让潜能生遇惑有帮助、遇挫有鼓励，让他们先学乐再乐学，让他们获得学习后的成就感、满足感，这样他们自然会找到课堂学习的存在感，对合作学习也会充满期望值。

（二）学生的展示习惯源于教师的撤退与放手

教师要“眼里有学生，心里想学生，一切为学生”。所以，教师不必总是站在学生和黑板之间，可适时撤退、放手，主动走下讲台，把讲台让给学生，把时间还给学生，把精彩留给学生；可借学生之口转达教师的意思，借学生之手展现教师的作为。

本节课在合作探索之后，我设计了一个操作展示的活动：动手画一个直角三角形，使其与给定直角三角形的一条直角边、一条斜边对应相等，然后判断两个直角三角形是否全等。在学生合作研讨之后，我放手交给学生展示、讲解。展示的学生讲述了自己解决问题的“心路历程”，讲自己开始是怎么做的，接着发现不是新方法，然后又是怎么做的。这次展示相对精彩，展示的作用自然放大，相当于无形之中的矫正和强化。

养成学生的展示习惯可以“两全齐美”。一“全”是面向全体学生。课堂展示可以让潜能生参与其中，进行伙伴联手的动态、静态展示。动态展示，伙伴同行，潜能生走上讲台，如遇困惑，同伴的指导如期而至，让讲解顺畅，让答案完整。静态展示，伙伴联手，潜能生尽力陈述观点，学优生如影随行，及时补充说明。二“全”是促进学生的全面发展。联手展示里有责任担当，有诚信共处。展示时，需要学优生与人为善，“不嫌贫不爱富”，诚恳对待同伴；需要潜能生与人为伴，不再游离于课堂之外，要参与学习，不让同伴失望。联手展示里有自强自信，有学会学习。人言生信，课堂上潜能生多展示、多表达，可以帮助他们树立学习自信。通过联手展示，可以养成学生良好的学习习惯，也能使潜能生转变学习态度，掌握学习方法，提高学习能力。而责任担当、诚信共处、自强自信、学会学习等都是学生发展所必备的品格和关键能力，有助于学生的全面发展。

二、让学生在分析与思维中提升数学能力

（一）学生的分析能力源于教师的意识与方法

学习数学需要分析能力，但培养学生分析问题的能力不是一日之功，需要教师有培养学生能力的意识、方法，并坚持不懈，形成习惯。

本课的例题是：如图1，AC⊥BC，BD⊥AD，AC=BD。求证：BC=AD。

图1

本题主要是训练学生运用直角三角形判定方法解决问题，同时刻意培养学生分析问题的能力。

一是培养学生识图的能力。当图形和题干出现时，应有意隐去结论，引导学生根据条件和图形联想相关的结论，同时注意引导学生挖掘图形中的隐含条件。

二是培养学生分析解题思路的能力。在数学课上经常会出现以下“尴尬”的场面：请某学生说说证明问题的思路，学生往往一说就非常彻底，一口气把解题过程说了出来，说得教师一时无语。究其原因，还是平时的训练不到位所致。实际上，说思路就是说怎么想的，怎么会想到的，而不是怎么去解决问题。在学生说思路时，要注意预先引领，让学生明确说思路就是由条件联想到什么结论，由求证的结论探索需要什么条件，能否满足，俗称“两头凑”。这样，才能培养学生正确的分析解题思路的能力。

（二）学生的思维能力源于教师的设问与引领

思维能力对于学生学习数学的重要性是不言而喻的。本节课注重对学生进行思维能力的训练，通过设计开放性的问题、习题的变式训练来促进学生思维能力的提升。

课始探究内容的添加条件时，例题呈现后的隐去结论，都属于开放性试题，有助于学生充分联想，综合运用所学知识；有助于学生迅速找到思维的起点以及解决问题的切入点。其实，例题的开放度还可以增加。题目出现后，可以问一下学生能够得到哪些结论，让学生大胆去展示、表达，最后写出欲求证的结论，再引导学生写出证明的过程。

如例题之后可安排练习：如图2，AB=CD，AE⊥BC，DF⊥BC，垂足分别为E，F，CE=BF。求证：AE=DF。

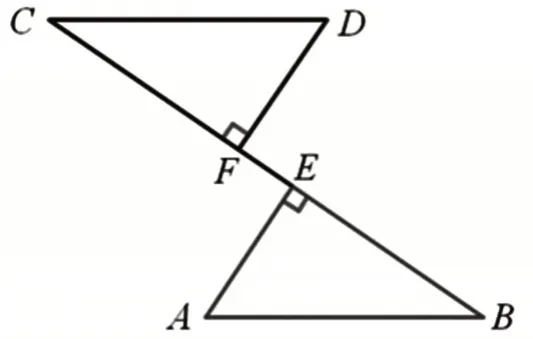
图2

练习之后，可以运用几何画板现场操作进行变式训练。通过把两个三角形拉开或推近，判断线段AE与DF的大小关系并证明。通过图形的相对运动，再回到原图形中进一步挖掘信息，让学生充分感知变式训练中的“变”与“不变”，形成辨析的思维能力，这才是变式训练的主要目的。