局部网格加密与嵌入式离散裂缝模型耦合预测压裂改造井产能
2020-04-01朱大伟胡永乐崔明月陈彦东梁冲蔡文新何艳辉王小勇陈辉李想
朱大伟,胡永乐,崔明月,陈彦东,梁冲,蔡文新,何艳辉,王小勇,陈辉,李想
(1.中国石油勘探开发研究院,北京 100083;2.中国石油中东公司哈法亚项目,北京 100034;3.北京大学,北京 100871)
0 引言
低渗、致密油气资源量规模巨大。随着国际能源需求的快速增长,低渗、致密油气资源的开发已成为国内外油气资源开发的热点[1-6]。人工压裂技术作为低渗、致密储集层开发的重要手段,近年来受到广泛关注,并取得了丰富的成果[6-9]。
考虑人工裂缝系统的压裂井产能数值模拟一直是行业难题。国内外学者将经过压裂改造后的致密储集层视为裂缝性油藏,并采用等效连续介质模型和离散裂缝模型(DFN)作为裂缝性致密储集层的流动模型[10-17]。等效连续介质模型(如双孔单渗模型、双孔双渗模型)可利用成熟孔隙介质理论,应用方便,是应用最为广泛的流动模型,但等效连续介质模型不能较好地描述裂缝的特殊导流能力,在单元体大小表征和等效渗透率确定方面也存在困难,因此,此两种模型并不适用于裂缝密度不大但存在控制流体流动方向的大尺度裂缝的储集层[11-14]。DFN能对裂缝进行表征,且DFN模型计算精度较高[15-17]。由于裂缝分布复杂,DFN往往基于非结构网格进行划分,其剖分过程繁琐,计算量庞大,尤其当裂缝相距较近时,网格剖分质量较差,存在病态网格,影响计算精度[18]。为了平衡计算效率和计算精度,Moinfar等[19-22]和Lee等[23-24]提出了嵌入式离散裂缝方法(EDFM)。EDFM直接采用结构化的基质网格,然后将裂缝嵌入到基质网格中作为额外网格。通过引入非相邻连接(NNC)来处理基质网格与裂缝网格的连接、裂缝网格与裂缝网格的连接。EDFM精确度优于等效连续介质模型,又避免了DFN复杂的非结构化网格剖分过程,大幅降低了计算复杂度,在压裂改造井产能预测方面具有很好的技术优势。然而,在压裂井的实际模拟中应用EDFM还存在以下问题:①实际油藏的地质模型网格往往由地质建模而来,通常是角点网格,且包含断层、尖灭等复杂地质构造,网格可能存在错层,现有的EDFM大多只支持正交网格[19-20,25-28],角点网格下应用EDFM难度大;②实际裂缝的开度是非均匀的,通常在缝口处开度最大,在裂缝尖端开度最小,现有EDFM将裂缝简化为渗透率均匀的薄片[19-20,25-27],这与实际不相符,影响模拟精度;③在油藏级别的数值模型中,基质网格尺寸往往较大(与人工裂缝尺寸相当甚至大于人工裂缝),在这种情况下,EDFM 方法很难准确描述近井地带复杂渗流过程。
本文提出一种高效计算嵌入式裂缝与基质网格之间传导率的方法,形成支持任意角点网格的 EDFM,并为嵌入式压裂裂缝设置非均质渗透率,在此基础上提出一种角点网格局部加密与嵌入式离散裂缝网络耦合预测压裂改造井产能的新方法。采用与DFN方法计算结果对比和拟合中东伊拉克第一口加砂压裂井历史生产数据的方法验证该方法的准确性和实用性。采用该方法,结合正交设计进行同区块首口分段压裂水平井改造参数的优化设计。
1 压裂井EDFM数值模型
本文采用黑油模型进行压裂改造井产能模拟。黑油模型假设气可以溶于油,气-水、油-水不互溶,油、水、气三相的流动都遵循多相流达西定律。
1.1 嵌入式离散裂缝
1.1.1 角点网格系统下嵌入式裂缝模型的建立
嵌入式离散裂缝模型中将裂缝处理为镶嵌在结构化网格中的二维面单元。本研究中,裂缝的基本单元采用四边形。一条裂缝可以由一个四边形表示,更复杂的裂缝可以由多个四边形组合而成。
大多数实际油藏模型中,网格系统采用角点网格,该网格系统采用(I,J,K)网格索引方式。在该系统下应用 EDFM,最重要的问题是网格的剖分、基质网格与嵌入式裂缝网格的传导率计算。
角点网格系统下EDFM的网格剖分、传导率计算步骤如下:①筛选所有与裂缝相交的基质网格,只要裂缝与基质网格的某条棱有交点,则裂缝与该基质网格相交(见图1a);②生成裂缝与基质网格的交面,交面是多边形,即裂缝片(见图1b);③根据裂缝轮廓剪裁交面,任意多边形轮廓均可通过程序实现,为简化计算,这里假设裂缝的轮廓均为四边形(见图1c);④计算基质网格与裂缝片之间的传导率;⑤搜索裂缝内部裂缝片的连接,计算裂缝片之间的传导率;⑥搜索裂缝与裂缝的连接,首先求出裂缝与裂缝的交线,然后计算共享交线裂缝片之间的传导率。

图1 嵌入式离散裂缝(EDFM)网格剖分示意图
当裂缝的尺寸大于基质网格时,基质网格与裂缝的交面小于裂缝,裂缝最终被离散为多个裂缝片(见图1c)。一个模型中通常有多个裂缝,每个裂缝都会被离散为一系列裂缝片。所有裂缝的裂缝片构成了一套网格系统,本文称之为“裂缝网格”,它是非结构网格,即不能用(I,J,K)编号。
计算基质网格与裂缝片之间、裂缝内部裂缝片之间、裂缝与裂缝之间的传导率主要采用 Lee等[23-24]和Moinfar等[19-20]的方法。这些传导率均为两点格式,用于离散后流动方程,用符号T表示。任意两个单元a至b的流动项都可以写为λT(Φa-Φb)。对于裂缝内部和裂缝之间的流动项,相对渗透率采用斜率为1的直线。
在裂缝内部,裂缝片与裂缝片之间的传导率按平面多边形的差分格式计算;对于裂缝与裂缝相交问题,假设裂缝片1、2相交(见图2a),传导率取共享交线裂缝片到交线传导率的调和平均:
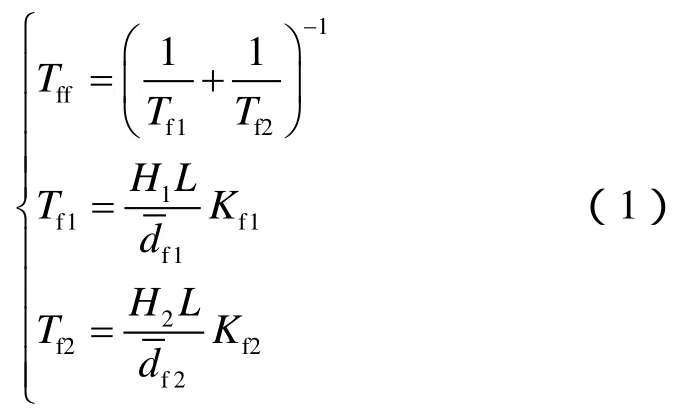
裂缝片内所有微元到交线的平均距离为:

一般来说,过交线的裂缝片都会被交线分割为两个子多边形,用Ⅰ、Ⅱ表示两个子多边形,则可以按(3)式计算。


图2 裂缝片与裂缝片、裂缝片与基质网格连接示意图
由于裂缝片嵌入在六面体基质网格内,基质网格与裂缝片之间的传导率无法按常规方法计算。基质网格与裂缝片之间的传导率等于:

如果基质渗透率是张量,则传导率等于:

基质网格到裂缝片的距离是基质的压力代表点与裂缝片压力代表点之间的距离。等于基质的每一个微元到裂缝片距离的平均值,可写为:

在求时,Moinfar等[19-20]采用的是数值积分,即将基质网格拆分为多个小单元,求的体积加权平均,此方法存在精度和效率问题。实际上,(6)式为6个四棱锥到裂缝片的距离的加权平均,可采用加权平均方法精确计算 6个四棱锥到裂缝片的距离,从而避免数值积分。如图2b所示,每个四棱锥的底分别是六面体的一个面,四棱锥的顶点都是裂缝片上的同一点,为方便计算,取裂缝片的第一个顶点为计算基点(图2b中K点),六面体到裂缝片KLMN的平均距离可表示为:

(7)式中“K-****”表示顶点为K的四棱锥,当四棱锥的底面在裂缝片同侧时(如K-BFIE),d等于四棱锥的质心到裂缝片的距离(四棱锥的质心在四棱锥的中轴线距顶点3/4处);当四棱锥的底面被裂缝片的某条边分割时(如K-BCGF,BCGF被LM分割),d等于两个棱锥(K-BLMF、K-LCGM)到裂缝片的距离的加权平均。图2b中,K-BCDE,K-CDHG的d均为零,体积也为零,这与四棱锥的顶点K的选取有关。只要K取裂缝片的某一个顶点,(7)式的值相同。
1.1.2 嵌入式裂缝非均质渗透率场
现有的EDFM将裂缝简化为渗透率均匀的薄片,这与地质实际不符,需要考虑裂缝内部渗透率的非均质性。为此,本文将压裂模拟软件计算结果中关于裂缝开度的点阵数据映射到嵌入式裂缝,利用开度数据计算嵌入式裂缝各裂缝片的渗透率。计算渗透率时假设裂缝中的流动是平板层流,因此裂缝的渗透率符合立方定律。裂缝上任一点x的渗透率等于其中,w(x)是裂缝在点x处的开度,K0是裂缝根部的渗透率,w0是裂缝根部的开度。裂缝根部即压裂井与裂缝相连的点,也是裂缝开度最大的位置。函数w(x)通过开度点阵数据线性插值得到。裂缝内某个裂缝片(其面积用Ω表示)的渗透率等于该裂缝片内所有点的渗透率的调和平均[28]:

可采用(8)式进行数值积分计算人工裂缝网格的非均质渗透率。渗透率等于零的裂缝片被视为无效网格,在模拟中剔除,不参与计算。
1.1.3 人工裂缝附近局部网格加密
EDFM 的优点在于裂缝不影响基质网格的形态,但基质网格步长过大会导致裂缝本身以及裂缝周围区域网格太稀疏,很难描述近井地带的复杂渗流过程,影响模拟精度。在实际油藏尺度下,人工压裂裂缝半长通常在数十米到200 m,而地质模型的网格步长可达100 m以上。如果直接使用地质模型建立数模模型,裂缝半翼在水平方向仅被离散为1~2个裂缝片,会给产能预测带来较大的误差。因此,本文提出一种局部网格加密(LGR)与嵌入式离散裂缝模型(EDFM)的耦合方法。首先正交加密近井地带的基质网格,然后将人工裂缝“嵌入”到加密后的基质网格中。由于基质网格更加细密,裂缝被基质网格切割后形成的裂缝片也更细密,即嵌入式裂缝的裂缝片随基质网格被加密,这提高了近井地带和裂缝内部流体流动计算的精确性。
LGR与EDFM同时使用使得裂缝的剖分过程十分复杂。在处理裂缝与基质网格的连接时,要考虑嵌入式裂缝片与加密网格的连接;在处理裂缝内部裂缝片的连接时,要考虑裂缝由基质网格进入加密区、裂缝跨加密区的情况。由于不同区域加密程度不同,穿过两个加密区的裂缝会出现相邻网格边界未对齐的情况(见图3),此时两网格之间的传导率要特殊处理。设两个网格单元a、b公共边的单位法向量是n,a、b中心到公共边界中点的向量分别是pa、pb,公共边界的长度为Lab,裂缝开度为H,则a、b之间的传导率计算公式为:


图3 未对齐网格传导率计算示意图
1.2 数值求解
基于 EDFM 的压裂井产能数值模型涉及基质网格、裂缝网格、井筒共 3组控制方程,构成了一套耦合的非线性方程组。在本研究中,为了保证求解耦合方程的收敛速度,采用全隐式法求解:用牛顿法求解非线性方程组,在生成雅克比矩阵时,要求取所有方程对所有自变量的导数,最终形成的雅克比矩阵为3×3的块状矩阵,由7部分构成。矩阵的3行分别对应基质网格、裂缝网格、井筒3组控制方程。矩阵的3列分别对应基质网格、裂缝网格、井筒 3组自变量(见图4)。图4中字母M、F、W分别代表基质、裂缝、井。在矩阵块的命名中,第一个字母代表方程,第二个字母代表变量,例如“MF”代表基质方程对裂缝变量的导数矩阵(基质方程中有流入裂缝的源汇项),“FW”代表裂缝方程对井变量的导数矩阵(裂缝方程中有流入井筒的源汇项)。本模型不考虑基质到井筒的流动,因此没有MW和WM矩阵。

图4 基质-裂缝-井筒耦合形成的线性方程组
2 致密储集层压裂直井实例
以中东伊拉克S储集层V5X井为例。S层储量占油田总储量的25%,但产能贡献不足1%。该层物性差,平均渗透率0.6×10-3μm2,平均孔隙度13%,属于“中孔低渗”碳酸盐岩储集层。
V5X井于2014年8月投产,前期进行了酸化、酸压增产措施,但产量低、有效期短,达不到配产要求,油井处于间开生产状态。为探索 S层有效动用工艺,2016年 12月对该井实施了伊拉克地区首次加砂压裂先导试验,入井总液量443.5 m3,总砂量39.6 m3,施工排量5.5 m3/min。压裂改造后,该井测试产油量217.8 m3/d,为改造前产量的9.4倍。压裂改造后一直采取控压生产,单井平均产量81.8 m3/d,压裂后3年累计增产油量约8.9×104m3,增产效果明显。
根据实际施工参数,利用压裂模拟软件(FracPro PT)对裂缝生长进行了模拟,得到了裂缝开度点阵数据、裂缝参数(见表1)。

表1 V5X井压裂施工后的裂缝参数
通过油藏工程分析得到V5X井控制范围为2 000 m×2 000 m,按井控范围从油藏模型中截出单井模型,属性数据保持与原模型一致。支撑裂缝半长94 m,基质网格步长100 m,此种情况下,对近井地带进行局部网格加密处理。利用压裂软件模拟V5X井裂缝生长过程,得到了裂缝初始开度,采用前述方法为嵌入式裂缝设置非均质渗透率。根据本文提出的方法,建立含EDFM 的单井模型。在模拟研究中,该井的生产方式设置为定产油量130.9 m3/d,同时设定最低井底压力为19.3 MPa。当定产油量生产至井底压力降至最低压力后转为定井底压力生产。
2.1 网格加密倍数
理论上,近井地带基质网格越密,计算精度越高。但当网格加密倍数达到一定程度后,计算精度提高幅度增长缓慢,但模型计算量大幅增加。因此,存在最佳的网格加密倍数。为此,利用压裂模拟软件得到的裂缝建立EDFM模型,以V5X井为中心,分别考虑不加密以及加密倍数为4,8,16,32情况下模拟压裂井的产能(见图5),统计累计产油量计算结果,并以加密32倍时累计产油量为基数,计算其他加密方式下累计产油量与基数的相对误差,结果见表2。

图5 不同加密倍数下压裂井日产油量、累计产油量变化

表2 不同加密倍数下的累计产油量计算结果对比
由图5和表2可以看出,模型加密后的产能预测结果与不加密时的差异较大。随着加密倍数的增加,压裂井生产能力整体呈现“增强”趋势。这是因为加密倍数较小时,近井地带基质网格尺寸大,无法描述近井地带人工裂缝存在时的复杂渗流过程,模拟结果误差较大。随着加密倍数的增加,稳产时间、累计产油量增加的幅度逐渐减小。在未加密算例中,基质网格的步长为 100 m,与裂缝半长接近。当加密倍数达16倍以上时,累计产油量模拟结果基本稳定,与加密32倍时的相对误差仅为-0.37%,说明V5X井近井地带加密倍数取16较为合适,既能保证计算精度,又能节省计算时间。实际模拟中,建议将基质网格的步长设置为水力裂缝半长的 1/10,计算精度和计算时间能取得较好的平衡。
需要说明的是裂缝渗透率分布的非均质性会对模拟结果产生较大影响,裂缝渗透率与裂缝开度成 3次方关系,且与缝长方向的变化相关。本算例中如果不考虑裂缝渗透率的非均质性,而统一采用裂缝根部渗透率,按照局部加密32倍模拟,生产3 000 d的累计产油量比考虑渗透率非均质性时高出11.1%,原因主要在于高估了人工裂缝的整体导流能力。考虑人工裂缝内部的渗透率非均质性与实际更相符。
2.2 验证案例
2.2.1 与DFN模型的对比验证
在EDFM与优化网格加密倍数的基础上,分别使用EDFM和DFN方法对案例进行了模拟,图6a为EDFM网格剖分结果;DFN采用垂直平分网格(PEBI),图6b为使用了201 312个单元的DFN网格剖分结果。图7对比了这两种方法模拟得到的产量。图8为 EDFM和DFN方法模拟的压裂后1 000 d的压力分布,EDFM模拟的产量、压力分布与DFN模拟的产量、压力分布基本一致。

图6 EDFM和DFN网格剖分示意图

图7 EDFM与DFN的模拟对比情况

图8 EDFM和DFN模型模拟压裂后1 000 d的压力分布
表3对比了EDFM和DFN的模拟参数。EDFM在保证计算精度的同时可大幅降低网格数量,显著节约计算成本,提高计算效率,在实际油藏模拟中具有较大技术优势。

表3 EDFM与DFN模型计算参数对比
2.2.2 与实际生产数据的拟合验证
对V5X井进行2个阶段(压裂前和压裂后)的历史拟合。采用定压力拟合产量方法对压裂前(2014年8月至2016年12月)生产进行历史拟合,在压裂前拟合的基础上建立重启文件,采用表1中的裂缝参数添加EDFM裂缝,拟合压裂后(2016年12月至2018年11月)生产历史(见图9),可以看出模型计算日产油量、井底流压与实际生产数据相关性较好,拟合程度高,模型的正确性与可靠性得到验证。

图9 V5X井历史拟合结果
3 致密储集层分段压裂水平井裂缝参数优化
继V5X先导试验井取得初步成功后,计划在同层位开展油田的首次分段压裂水平井先导试验。为此,利用建立的“LGR+EDFM”耦合模型方法,对工区的分段压裂水平井进行裂缝参数优化,指导工艺方案设计。使用EDFM在实际应用中具有2个优势:①在修改裂缝的尺寸和段距时,不用重新剖分网格;②基质网格保持不变,算例之间更具对比性。
3.1 模型建立
通过压裂模拟软件确定裂缝形态参数,导入油藏数值模拟模型,对近井地带网格进行加密,然后利用EDFM方法对人工裂缝进行建模(见图10)。水平井的生产方式设置为定产油量245.5 m3/d,同时设定最低井底压力为19.3 MPa。当定产油量生产至井底压力降至最低压力后转为定井底压力生产。

图10 分段压裂水平井LGR+EDFM耦合模型
3.2 改造参数优化
取水平段长度为600,800,1 000 m,压裂段数为6,8,10段,裂缝半长为110,130,150 m,裂缝导流能力为20,40,60 μm2·cm,模拟计算水平井产能。根据正交设计原则,共设计9套正交试验方案(见表4)。

表4 正交试验设计方案
9套方案条件下水平井累计产油量的模拟结果如图11所示。可以看出,水平井累计产油量以方案7最大,方案1最小,从大到小排序为方案7、方案8、方案9、方案4、方案6、方案5、方案3、方案2、方案1;水平井产能对水平段长度最敏感,水平段长度1 000 m方案累计产油量大于800 m与600 m方案。总体方案7的设计参数最优,压裂水平井产能最大。

图11 不同方案下水平井累计产油量对比图
4 结论
针对现有EDFM对角点网格不兼容、近井地带精度低、不考虑裂缝内导流能力的非均质性等问题,设计了一种角点网格下的 EDFM,可实现嵌入式裂缝与基质网格传导率高效计算。利用人工裂缝开度点阵数据计算嵌入式裂缝各裂缝片的渗透率,在此基础上提出一种局部网格加密与嵌入式离散裂缝模型耦合求解预测压裂改造井产能的方法。
通过与DFN方法计算结果对比及中东加砂压裂井实际生产数据的拟合,验证了方法的有效性。采用该方法,结合正交设计可进行分段压裂水平井改造参数的优化设计,推荐优化工艺参数。本文提出的方法对提高EDFM方法适应性及产能预测精度具有理论意义且实用性强,实现了油藏尺度下裂缝模拟与产能数值模拟的耦合衔接。
符号注释:
a,b——网格单元;A——基质网格或单位控制体内裂缝的面积,m2;d——四棱锥的高,m;——基质的每个微元到多边形的距离的平均值,m;d——面微元到交线的垂直向量,m;——裂缝片内所有微元到交线的平均距离,m;,——裂缝片1、2内所有微元到交线的平均距离,m;dI,dII——两个子多边形的重心到交线的距离,m;H——裂缝开度,m;H1,H2——裂缝片1、2的开度,m;I,J,K——网格编号索引符号;K0——裂缝根部的渗透率,10-3μm2;Ka,Kb——基质网格单元a、b的渗透率,10-3μm2;Kf1,Kf2——裂缝片1、2的渗透率,10-3μm2;Km——基质渗透率,10-3μm2;Km——基质的渗透率张量,10-3μm2;KΩ——裂缝片内面积为Ω的多边形的渗透率,10-3μm2;Lab——两条裂缝间交线的长度,m;n——网格单元a、b公共边的单位法向量;nA——裂缝片单元A的外法线向量;pa,pb——网格单元a、b中心到公共边界中点的向量;r——余误差;S——裂缝片面积,m2;SI,SII——子多边形的面积,m2;T——传导率,10-3μm2·m;Tab——a,b网格单元之间的传导率,10-3μm2·m;Tf1,Tf2——裂缝片 1、2到交线的传导率,10-3μm2·m;Tff——调和平均传导率,10-3μm2·m;Tmf——基质网格与裂缝片之间的传导率,10-3μm2·m;V——基质网格的体积,m3;w0——裂缝根部的开度,m;w(x)——裂缝在点x的开度,m;x——裂缝内部节点坐标,m;ΔX——自变量增量;λ——流体流度,10-3μm2/(mPa·s);Φa,Φb——网格单元a、b的压力势或水头,MPa;Ω——裂缝片面积,m2。下标:F——裂缝;M——基质;W——井筒。
