颗粒负荷对小型旋风器性能影响的模拟分析

任欢，赵兵涛，王东燊，张芸

（1上海理工大学能源与动力工程学院，上海200093；2上海市动力工程多相流动与传热重点实验室，上海200093）

旋风器因其结构简单、运行成本低廉和适用操作条件广泛的特点，在石油化工、煤炭发电和环境保护等方面都发挥着重要作用[1-2]。

为较好分离捕集5μm 以下的超细颗粒，减小结构尺寸的小型旋风器设计受到广泛关注[3-4]。相较于中大型旋风器，小型旋风器由于筒体直径较小（低至0.1m 以下），不仅减少了能量损耗，而且加强了静态离心力对气固两相分离的强化作用，使其在捕捉微米级颗粒（＜5μm）方面拥有一定的优势[5-6]。其次，作为高性能采样器应用于微细颗粒PM2.5的取样监测中也占有重要地位[7-8]。最后，利用小型旋风器对超细物料的分级分选也得到了广泛发展[9-10]。综合以往的研究，如何较好地预测小型旋风器内气相的流体动力学和颗粒运动是一个难题，深入研究开发能分离细微固相颗粒的高效小型化旋风器及其分离技术势在必行。

在关于旋风器内气固两相流动的数值模拟研究中，大多数[11-12]采用离散相模型（DPM）考虑了气相和颗粒之间的单、双向耦合，但忽略颗粒碰撞的影响，并且只适用于颗粒负荷较低的情况。在颗粒负荷较高时，离散元方法（DEM）可以进行模拟[13]，然而本次研究的小型旋风器内颗粒尺寸分布较小（≤5μm），与颗粒模型相关的计算成本非常高，因此并不适用。采用欧拉-欧拉方法中的多相流混合（Mixture）模型，可以很好地节约计算成本，并且在模拟较高颗粒负荷下的气固两相流场可获得和实际较为符合的结果[14-16]。

本文选择自行设计筒体直径为25mm的小型旋风器，采用RSM 和Mixture 模型计算旋风器内的气固两相流，在考虑气体-颗粒相间耦合及颗粒碰撞的条件下，考察不同流量、颗粒浓度变化对旋风器内流场分布、分离效率和压降的影响，以期对小型旋风器内气固两相流动的认识，操作的优化提供指导。

1 实验和方法

1.1 旋风器设计

旋风器几何结构和尺寸如图1(a)所示，入口段长度为25mm。采用ICEM 将整个旋风器的几何模型划分为若干块，圆柱及锥体部分采用O 形剖分，壁面边界加密，网格生成如图1(b)。

1.2 实验

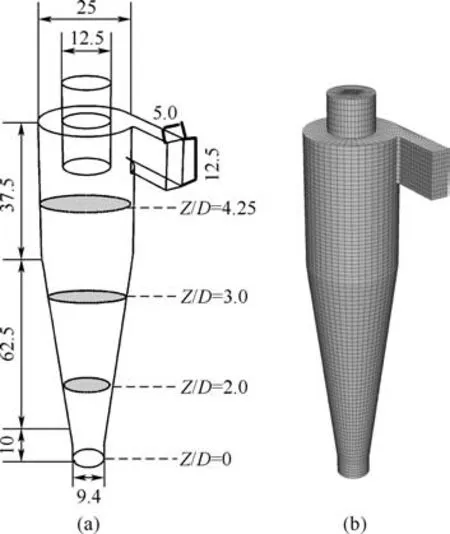
图1 旋风器几何尺寸及网格划分（单位：mm）

图2 旋风器压降实验系统

采用此小型旋风器，在不同给定流量下（20～100L/min）进行纯气相流场的压降实验。旋风器的压降测量系统如图2 所示，环境空气作为工作气体，由两台并联无油空气压缩机（OTS-1100，公称容积流量100L/min，额定排气压力0.7MPa）向旋风器中充气。流量由阀门控制，质量流量计（MF5712-N-200，量程0～200L/min，最大工作压力0.8MPa）测量。采用智能数字微压计（DP1000-IIIB，量程0～±8000Pa，精度1 级，分辨率1Pa）测量旋风器的压降。实验在293K±1K、103kPa 条件下进行。

2 数值计算模型

2.1 湍流模型

RSM 基于各向异性假设对旋风器内的强旋流流动有较好的模拟性能，其输运方程可简化为式(1)[17]。

式中，Qij为扩散输运项；Pij为应力产生项；ψij为压力应力关联项；εij为耗散项。

2.2 两相流模型

基于欧拉-欧拉方法的Mixture模型，将气固两相看作连续介质计算，二者是相互渗透相互影响的连续相流体，在欧拉坐标系下采用连续流体的质量和动量方程守恒方程来描述[14-16]。

Mixture模型的连续性方程见式(2)。

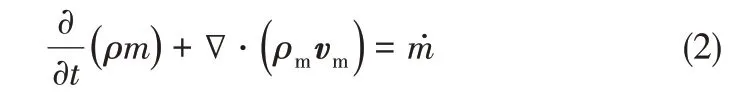
Mixture模型的动量方程见式(3)。

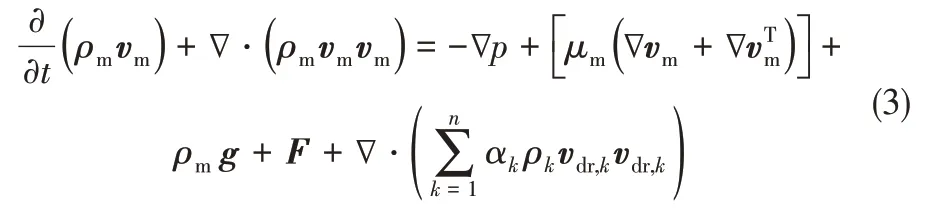
第二相的体积分数方程见式(4)。

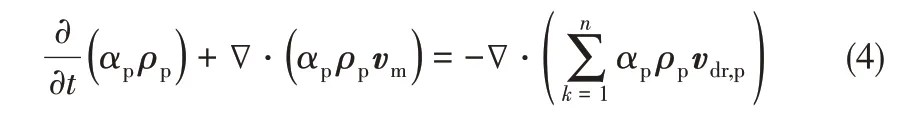
式中，vm是质量平均速度；ρm是混合物密度，n表示相的数目；μm为混合相的动力黏度；m˙是质量源的质量传递；F为体积力；vdr,k为滑移速度。

混合模型中的固体压力可用式(5)计算[18]。

式中，epq=0.9 为颗粒相间的碰撞系数；g0,pq为径向分布函数，表征颗粒间的碰撞概率。

2.3 模拟条件及求解策略

气相条件为空气，模拟温度为25℃。入口采用速度型入口（velocity-inlet），顶部和底部出口设为压力型出口（pressure-outlet），压力大小为大气压，其他均设为无滑移壁面。颗粒密度为2500 kg/m3，由于旋风器内部颗粒粒径分布范围较广，采用近似处理将分布较宽的颗粒简化为几种主要粒径，在Mixture 模型中将不同粒径的颗粒视作不同的相，其体积分数分布如表1。在给定的流量下，采用5种不同的颗粒浓度进行数值模拟，颗粒质量负荷如表2。压力-速度耦合算法采用SIMPLEC 算法，压力插补格式采用PRESTO!，离散格式采用QUICK 格式。先采取稳态求解单相气态流场，残差均收敛至10-3。再采取非稳态求解方式，加入颗粒源进行相间耦合计算，时间步长设定成10-4s，模拟残差设置为10-5。进出口流量误差小于0.001%时，认为结果收敛。

表1 颗粒粒径分布

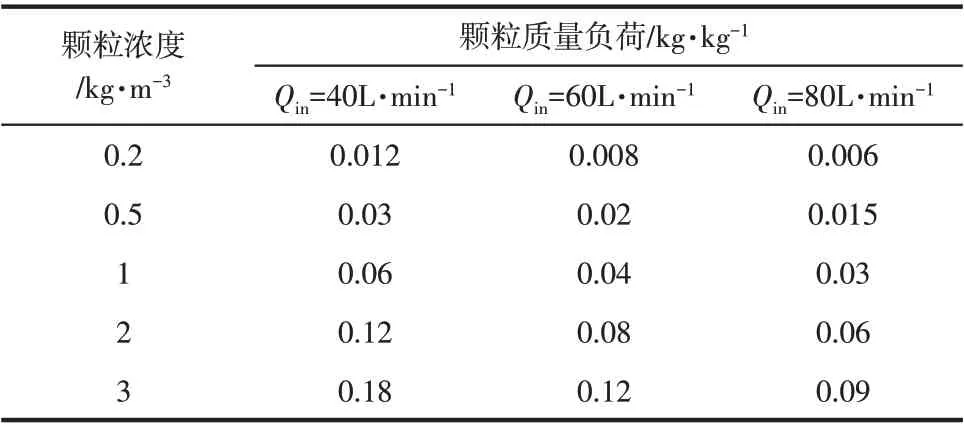
表2 颗粒质量负荷

3 结果与讨论

3.1 数学模型及网格无关性验证

基于RSM 对每个实验工况进行数值模拟，得到的数值模拟压降和实验结果如图3(a)所示，二者的误差小于10%，说明RSM 能够很好地表征旋风器的压降特性。并且可以看到，随着入口流量的增大，压降呈现非线性单调递增。图3(b)为基于RSM和Mixture 模型对于Young 等[19]的实验进行数值模拟，实验结果和模拟结果总体趋势相同，误差小于15%，说明RSM 和Mixture 模型能够很好地预测旋风器的分离效率。综上证明，经实验数据验证的数学模型切实可行。

为排除网格数量对模拟结果的影响，进行网格无关性验证如图4。划分44565（粗网格）、86752（中网格）和122467（细网格）三种网格数量，粗网格和细网格的切向速度相对于中网格的平均相对误差分别为3.4%和6.2%，在可接受范围。另外考虑到旋风器内强旋转流场的复杂性以及计算成本，本文确定采用中等数量的网格数。

3.2 颗粒负荷对气相流场的影响

图5(a)为旋风器垂直中心平面不同入口颗粒浓度（Qin=60L/min）下流场的静压分布云图。图6为不同截面处静压分布线图。在其他流量下的模拟结果呈现只是量值具有差异的相似流场分布。此小型旋风器内部流场分布形态与中大型类似。每个浓度下的旋风器均是壁面处压力较大，轴中心处压力值为负，与纯气相流场相比，颗粒负荷后旋风器排气管处负压区消失，这表明，与其他区域相比，固体颗粒旋风器顶部的气流影响更大。另一个明显趋势是随着颗粒浓度增加，旋风器中心区域的负压区长度减小，不同截面处静压值逐渐减小。

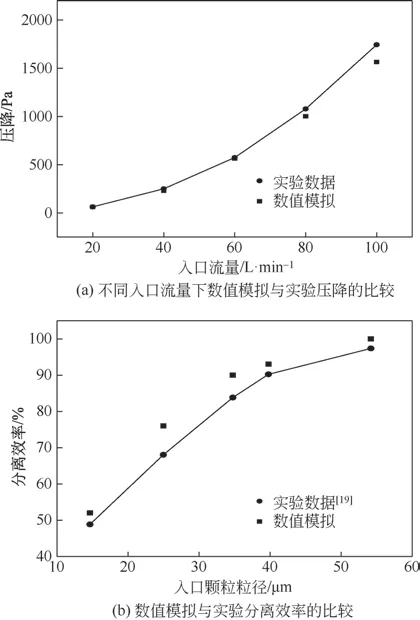
图3 数学模型验证

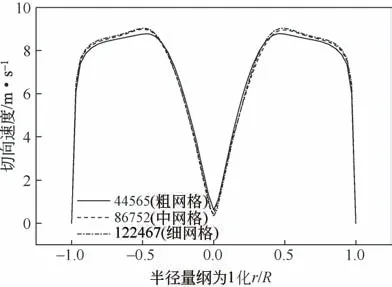
图4 网格无关性验证

图5(b)为旋风器垂直中心平面不同入口颗粒浓度下切向速度分布云图。图7为不同截面处切向速度分布线图。切向速度是决定离心力的主要因素，在颗粒分离中起着重要作用。旋风器的切向速度分布呈M形，为典型的Rankine涡分布。与纯气相流场相比，颗粒负荷明显改变切向速度的分布形态，并且速度的量值低于纯气相流场。在浓度为0.5 kg/m3、1kg/m3和2kg/m3时，截面Z/D=4.25处切向速度峰值相较于纯气相流场分别减小37.3%、41.4%和44.1%。在同一浓度范围内，沿轴向向下切向速度逐渐减小。随着颗粒浓度的增大，气相的切向速度减少越多，这与Yuu等[20]在实验中得到的结论相符。颗粒的存在阻碍气体的流动，颗粒对气相的反作用力主要沿切向，颗粒浓度越大，反作用力越大，切向速度越小。

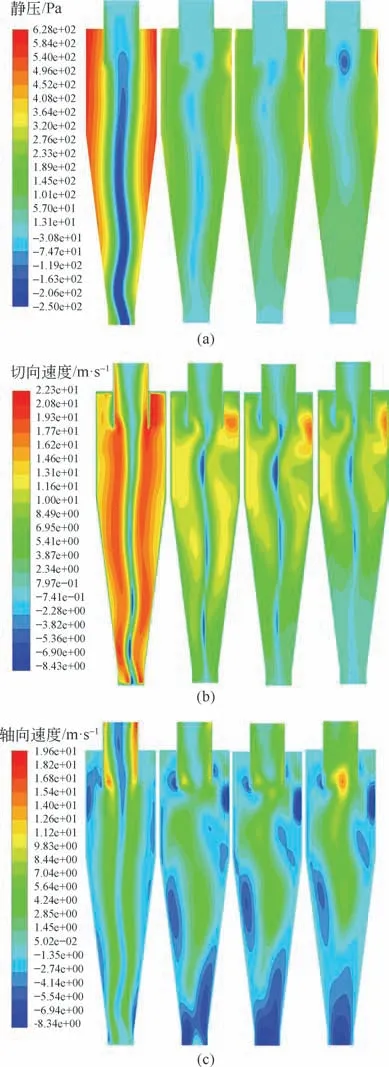
图5 不同入口颗粒浓度（Cin=0、0.5kg/m3、1kg/m3和2kg/m3）旋风器内气相流场静压、切向和轴向速度的分布云图

图6 不同入口颗粒浓度（Cin=0、0.5kg/m3、1kg/m3和2kg/m3）旋风器在不同截面处气相流场的静压分布线图

图5(c)为旋风器垂直中心平面不同入口颗粒浓度下轴向速度分布云图。图8为不同截面处轴向速度分布线图。轴向流场分为中心上行和外层下行双层旋流流动。沉积在壁面附近的颗粒通过轴向速度来实现向下运动，轴向速度决定了其在旋风器中的停留时间。在纯气相流场，由于排气芯管附近的流体摩擦出现涡流损失，形成正向压力梯度，轴向速度中心凹陷。颗粒负荷影响轴向速度分布的稳定性，使其分布不规则；另一方面，随着颗粒浓度的增大，轴向速度在上行流区和下行流区均减小。

3.3 颗粒负荷对分离效率的影响

图7 不同入口颗粒浓度（Cin=0、0.5kg/m3、1kg/m3和2kg/m3）旋风器在不同截面处气相流场的切向速度分布线图

分离效率是评价旋风器性能的重要标准之一，其定义为旋风器底部出口颗粒的质量流量与入口处的质量流量的比值[21]。图9为不同流量下，旋风器不同粒径颗粒的分级效率。可以看到，在不同流量和浓度下，此小型旋风器较中大型旋风器对于2～5μm 颗粒均有着接近于100%的分离效率。随着流量的增大，0.5μm和1μm颗粒的分级效率先增大后趋于平缓；随着浓度的增大，二者分离效率逐渐增大。

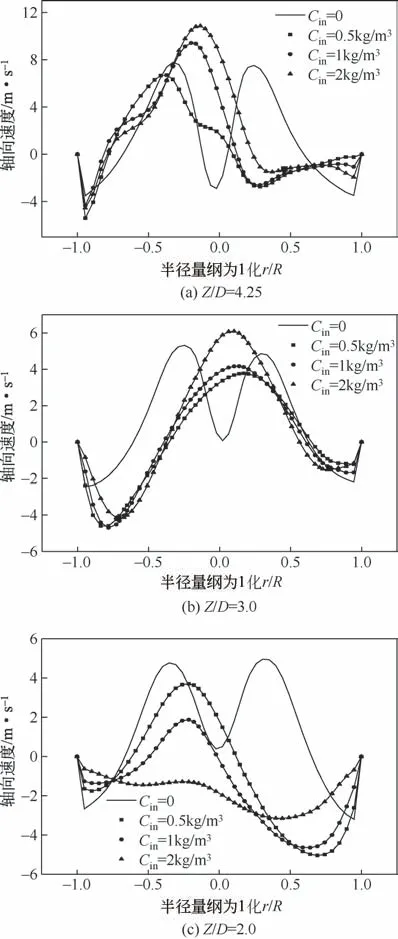
图8 不同入口颗粒浓度（Cin=0、0.5kg/m3、1kg/m3和2kg/m3）旋风器在不同截面处气相流场的轴向速度分布线图

图10为不同流量、浓度下颗粒的总分离效率。在同一入口浓度，随着入口流量的增大，分离效率呈现先增大后减小的趋势。随着入口流量的增大，旋风器内部颗粒受到的离心力增大，快速向器壁迁移，分离效率增大；而当入口流量增大至临界值时，短路流和二次湍流加剧，导致旋风器的分离效率下降[22]。在同一流量，随着入口颗粒浓度的增大，分离效率增大。随着颗粒浓度的增加，切向速度减小，降低了颗粒向壁面移动的驱动力[12]；同时也增加了小粒径颗粒从排气口逃逸的概率，从而降低了分离效率。另一方面，颗粒间相互作用加强，如碰撞团聚等作用会提高分离效率[23-24]。此外，在一定流量下，旋风器内的旋转气流对颗粒存在临界携带量，超过此部分的颗粒会脱离旋转气流向壁面运动分离出来增加分离效率，故在本次模拟颗粒浓度在0.2～3kg/m3的范围内，分离效率逐渐增大，在浓度大于0.5kg/m3后，增加幅度不大。

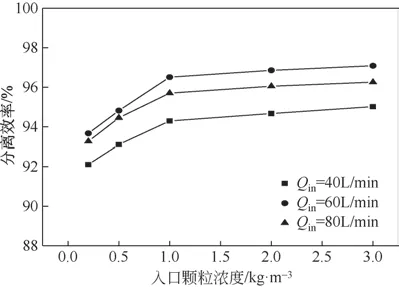
图10 不同流量、浓度下颗粒的分离效率

3.4 颗粒负荷对压降的影响

压降是评价旋风器性能的另一重要标准，定义为入口与排气口静压压差[16]。图11 为入口流量、浓度变化对旋风器压降的影响。在同一浓度下，随着流量的增大，旋风器的压降呈非线性增加。随着入口流量的增大，速度逐渐增大，进、出口能量损失增大，湍流强度增大，旋流损失等增大，造成压降损失也就越大[22]。在同一流量下，随着入口颗粒浓度的增大，压降呈现先减小后增大的趋势，存在临界颗粒浓度值为0.5kg/m3，在定性上与陈建义等[25]的结论一致。随着入口颗粒浓度的增大，切向速度减小，旋流损失减弱是使压降减小的主要原因[13]。其次，颗粒向壁面移动时，会干扰气流在壁面的凝集条件，使气流与壁面之间的摩擦力减小，从而减小摩擦损失[20]。另一方面，随着入口颗粒浓度的增大，进、出口处的局部流动损失会因气固两相混合物密度增大而有所增加，从而增大压降。在多种因素的相互作用下，入口颗粒浓度对压降展现出双重作用[25]。

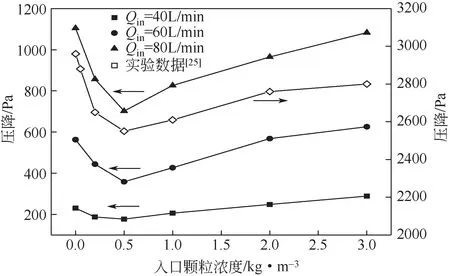
图11 不同入口流量、浓度下的压降

事实上，颗粒负荷对旋风器压降的影响是一个复杂的过程，二者之间的关系已经观察到3种不同类型的结果，有研究者[26-27]发现旋风器压降随着入口颗粒浓度的增大而减小，最后趋于恒定。其他结果表明[13,28]，旋风器的压降与颗粒浓度呈负相关，压降随着入口固体浓度的增加而减小。同样有研究与本文结果一致[25,29-30]，随着固体颗粒浓度的增大，压降先减小后增大呈U形。压降受旋风器几何形状及运行工况的影响，不同模型不同工况造成颗粒负荷对压降影响的差异。

4 结论

（1）经模拟验证表明，基于RSM 和Mixture 模型考虑气体和颗粒的相间耦合及颗粒间的碰撞，能较好地模拟颗粒负荷下小型旋风器内气固两相流场、分离效率和压降特性。

（2）颗粒的存在会明显改变流场分布，随着颗粒浓度的增大，旋风器中心区域的负压区长度减小，壁面附近的压力值逐渐减小；切向和轴向速度逐渐减小。

（3）在同一浓度下，随着入口流量的增大，旋风器的分离效率先增大后减小，压降呈非线性增大。在同一流量下，随着颗粒浓度的增大，旋风器的分离效率逐渐增大，压降先减小后增大。流量在40～80L/min，浓度在0.2～3kg/m3范围内，对于此小型旋风器存在最佳操作工况：入口流量60L/min，颗粒浓度0.5kg/m3。