深水双梯度钻井井口回压实时优化与最大钻进深度预测

2020-04-01王江帅李军王烊柳贡慧李汉兴

石油科学通报 2020年1期

王江帅，李军*，王烊，柳贡慧, ，李汉兴

1 中国石油大学(北京)石油工程学院，北京 102249 2 中海油能源发展股份有限公司山西分公司，晋中 030600 3 北京工业大学，北京 100192 4 中海油研究总院有限责任公司，北京 100028

0 引言

为解决深水窄压力窗口安全钻井问题[1-3]，国内外相关研究机构和学者分别开展了注轻质介质(气体、空心球)双梯度钻井[4-5]、海底泵举升钻井[6]以及控制泥浆帽钻井[7-9]等钻井技术的研究，研制了相关核心技术和配套装备，发展了与该类钻井技术相关的钻井理论。近年来，王江帅等人提出了一种基于井下分离的新型深水双梯度钻井方式，并开展了室内循环分离实验，证明了分离器的有效性和井筒内双压力梯度的可行性[10-11]。与常规钻井方式相比，基于井下分离的深水双梯度钻井井筒压力具有动态变化的显著特征。钻进过程中井深逐渐增加，分离器随钻头向下移动，井筒压力梯度拐点随之改变，导致深水双梯度钻井钻进过程中的井筒压力发生动态变化。

基于动态井筒压力计算方法，王江帅等人建立了钻井参数优化模型[11]，通过优化分离器与钻头间距、分离效率、空心球注入体积分数、纯钻井液密度、井口回压、排量等参数，保证了钻进过程中的动态井筒压力始终位于窄安全压力窗口内，一定程度上延伸了钻进深度。然而，由于模型建立过程中井口回压被设定为恒定值，钻进过程中无法调节井口回压值以得到具有时效性的最优井筒压力剖面，限制了钻进深度进一步延伸。因此，基于已有研究的不足，考虑到钻井过程中井口回压调节简便、压力传递迅速等优点[12-13]，本文建立了井口回压实时调节优化模型，模型通过优化实时钻进过程中的井口回压，达到实时优化井筒压力剖面的效果，从而实现更大的钻进深度，有利于进一步简化深水钻井井身结构，降低钻井综合成本。

1 钻进过程中动态井筒压力计算

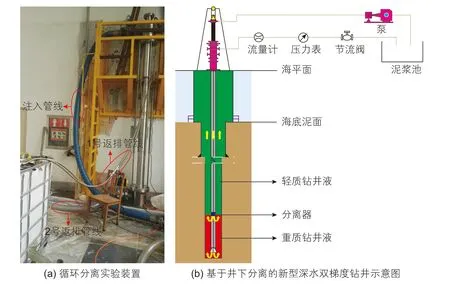
图1 深水双梯度钻井示意图Fig. 1 Diagram of deepwater dual-gradient drilling

如图1所示的室内循环分离实验装置和基于井下分离的新型深水双梯度钻井示意图。前期开展了室内循环分离实验，证明了分离器的有效性，分离效率在40%左右[11]。循环过程中，混合钻井液(一定比例的空心球与纯钻井液配制而成的混合物)通过泵注入钻杆内，混合钻井液流经分离器时部分空心球被分离并进入环空，因此以分离器位置为界线，上部环空空心球含量高，下部环空空心球含量低。由于空心球比重低于纯钻井液，因此，分离器上部环空为轻质钻井液，下部环空为重质钻井液。

如图2所示，钻进过程中分离器随井深的增加而下移，使得目标点处轻质钻井液井段长度增加，而重质钻井液井段长度减小，因此导致目标点井深处井筒压力发生变化。图中目标点指井筒裸眼段内具有相同深度的任意位置点，由a到c，井深增加，分离器向下移动，目标点压力组成发生变化。

对于状态a而言，循环钻井过程中目标点处的压力计算如下：

其中，Pa为状态a下的目标点压力，Pa；Pcp为井口回压，Pa；ρ1为轻质钻井液密度，kg/m3；ρ2为重质钻井液密度，kg/m3；H11为状态a下的轻质钻井液段长度，m；H12为状态a下分离器与目标点之间的重质钻井液段长度，m；△Pf1为单位长度轻质钻井液段的循环压耗，Pa/m；△Pf2为单位长度重质钻井液段的循环压耗，Pa/m；g为重力加速度，取9.81 m/s2；θ为井斜角，o。

公式(1)中ρ1、ρ2、H11、H12、△Pf1、△Pf2与分离器分离效率、空心球注入体积分数、纯钻井液密度、分离器与钻头间距、排量等参数有关，具体计算方法详见文献[11,14]。

对于状态b和c而言，其井筒压力分别如下式：

其中Pb为状态b下的目标点压力，Pa；H21为状态b下的轻质钻井液段长度，m；H22为状态b下分离器与目标点之间的重质钻井液段长度，m。

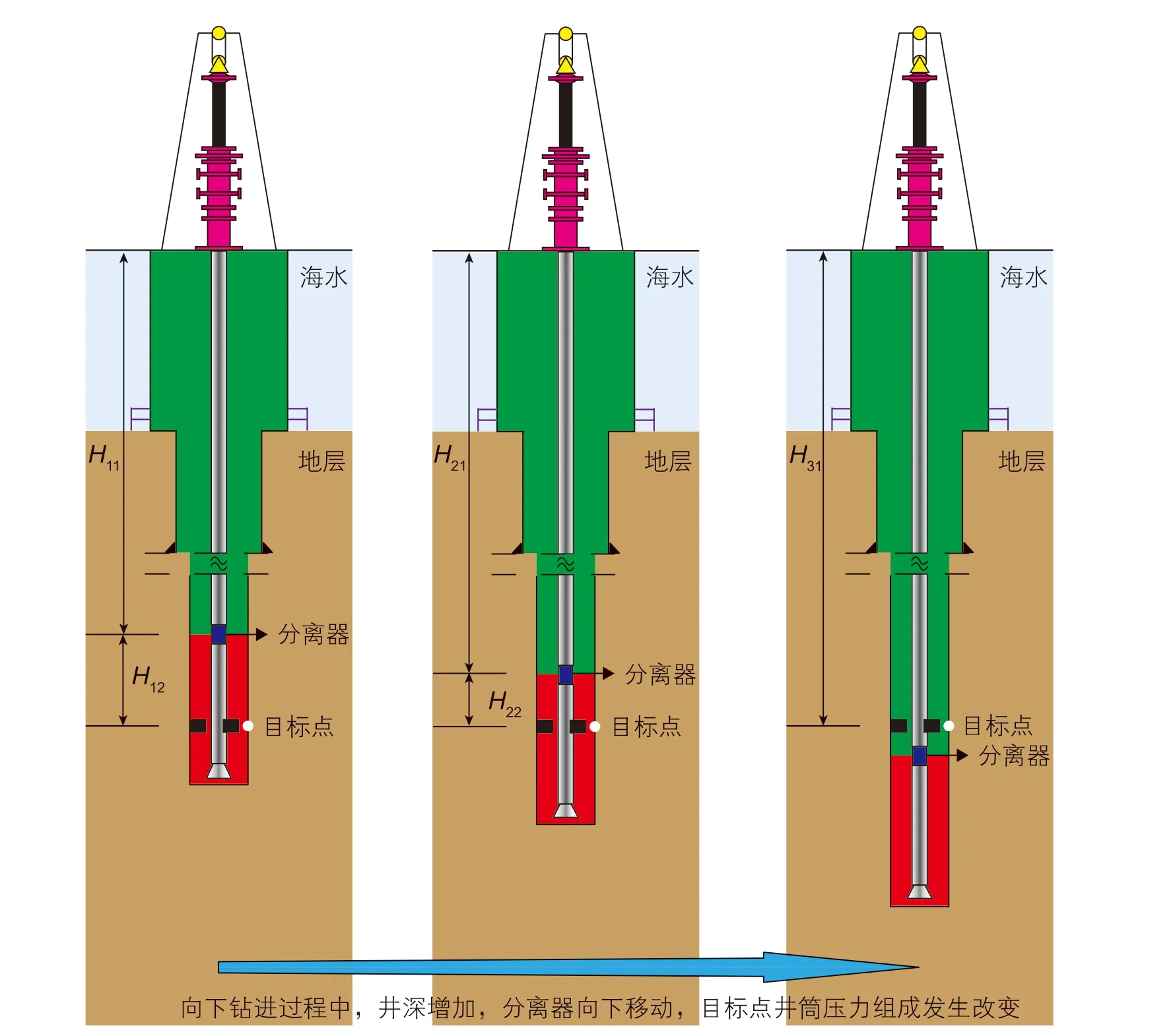
图2 钻进过程中目标点井筒压力组成Fig. 2 Composition of wellbore pressure of target point during drilling process

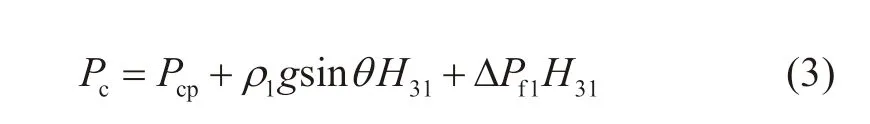
其中Pc为状态c下的目标点压力，Pa；H31为状态c下的轻质钻井液段长度，m。

综合公式(1～3)可以看出，不同状态下轻质钻井液和重质钻井液所占的井筒长度比例不同，因此不同状态下的目标点井筒压力不再相等。即，

由以上分析可知，任意状态下目标点压力均与井口回压Pcp密切相关，钻进过程中可以通过实时优化井口回压，达到实时优化井筒压力剖面的效果，从而实现更大的钻进深度，简化深水钻井井身结构，降低钻井综合成本。所以，建立井口回压实时调节优化模型，并研究回压实时调节条件下的最大钻进深度具有重要意义。

2 井口回压实时调节优化模型建立与求解

2.1 目标函数

井口回压实时调节优化模型的目的是在最优分离器与钻头间距、分离效率、空心球注入体积分数、纯钻井液密度、排量的前提下，通过优化实时钻进过程中的井口回压，达到实时优化井筒压力剖面的效果，从而实现更大的钻进深度。由于无法建立钻进深度与井口回压之间的直接关系，因此将钻进深度作为目标函数在数学上不可行，无法实现优化求解。本文采用当前井深处的井底压差作为目标函数，并将裸眼段任意点的井筒压力和回压取值范围作为约束条件。既实现了最小化井底压差，又保证了最大的钻进深度。最优化模型用数学语言表示如下：

上式中，f(Pcp)为目标函数，定义为当前井深处的井底压差，表达式如下：

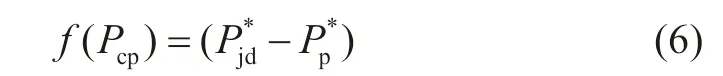
其中，P*p为当前井深处的地层孔隙压力，Pa；P*jd为当前井深处的井底压力，Pa。P*jd的具体计算公式如下：

其中，L*为当前井底深度，m，该值随着钻进的进行而增加；H20为分离器与目标点之间的距离，m。

2.2 约束条件

模拟的约束条件：

2.3 模型求解

目标函数定义为当前井深处井底压差，钻进过程中目标函数是动态变化的；另外，随着井深的增加，压力约束条件增多，由于裸眼段任意点的井筒压力是变化的，所以约束条件也呈动态变化。由以上分析可知，该问题是一个有约束的非线性动态最优化问题，将该动态最优化问题分解为有限个静态的有约束非线性最优化问题，利用最优化方法进行求解。

序列二次规划(SQP)方法被认为是用来解决有约束的非线性最优化问题的最有效方法之一[15]，该方法在工程方面具有重要的应用价值，本文采用该算法进行模型求解。选取MATLAB中的fmincon函数作为目标函数，调用SQP算法求解原始最优控制问题参数化的非线性规划(NLP)问题。fmincon函数具体表示如下：

x为矩阵，返回满足最优化目标函数的实时井口回压值，即钻进深度达到最大，井底压差达到最小时的井口回压值；fval为数组，返回最优化目标函数的值，即钻进深度达到最大时的最小井底压差值；exitflag为数组，利用该值可判断优化模型能否在满足约束条件的情况下实现正常钻进，约束条件下能够钻达的井深处返回值为1，不能钻达的井深处返回值为非1，因此可根据其返回值情况得出约束条件下的最大钻进井深。fun为目标函数；x0为变量初值；A和b组成变量的线性等式约束条件；Aeq和beq组成变量的线性不等式约束条件；lb、ub为变量的上下界；nonlcon为变量的非线性不等式约束条件。

3 实例分析

模拟井为一口深水直井，基础数据如下：水深1000 m，已钻井深1200 m，下套管固井；隔水管外径660.4mm，内径609.6 mm，钻杆外径127 mm，内径101.6 mm，表层套管内径457.2 mm，钻头342.9 mm。已知1200～2200 m的窄安全压力窗口，模拟时设定的极限井深为2200 m，钻进到该深度时，模拟结束。

3.1 回压恒定和回压实时调节两种条件下优化结果对比

回压实时调节条件下进行优化模拟时，以回压恒定条件下模拟得到的最优分离器与钻头间距、分离效率、空心球注入体积分数、钻井液密度、排量等钻井参数为基础，优化实时钻进过程中的井口回压，对比分析两种条件下的最大钻进深度。

窄压力窗口为1.03～1.05 g/cm3时，分别取三组不同的最优钻井参数组合[11]进行井口回压优化设计，优化结果见表1和图3～5。

表1给出了三种最优钻井参数组合时，回压恒定和回压实时调节两种条件下最大钻进深度值，图3给出了回压实时调节条件下三种最优钻井参数组合的最大钻进深度返回值。综合表1和图3可以看出，与回压恒定条件下的模拟结果相比，回压实时调节条件下的最大钻进深度普遍增加。三种最优钻井参数组合条件下的最大钻进深度分别由1440 m、1510 m、1550 m增加到1450 m、1650 m、1660 m(该值可由图3看出，返回值为1的截止深度为最大钻进深度)，最大钻进深度明显增加。

表1 回压恒定和回压实时调节两种条件下最大钻进深度对比Table 1 Comparison of maximum drilling depth under two conditions of constant backpressure and real-time adjustment of backpressure

图4给出了三种最优钻井参数组合时，回压恒定和回压实时调节两种条件下实时钻进过程中的最优井口回压。可以看出，回压恒定条件下的最优井口回压值一直保持恒定，而回压实时调节条件下的最优井口回压值随着井深的增加实时改变。钻进过程中实时调节井口回压可更好的优化井筒压力剖面，以适应窄压力窗口，实现更大的钻进深度。

图3 回压实时调节条件下的最大钻进深度表征值Fig. 3 The value to characterize the maximum drilling depth under real-time adjustment of backpressure

图4 回压恒定和回压实时调节两种条件下的最优井口回压Fig. 4 Optimum wellhead backpressure under two conditions of constant backpressure and real-time adjustment of backpressure

图5给出了回压实时调节条件下三种最优钻井参数组合的随钻井底压差。可以看出，钻进过程中的井底压差值均大于零，也就是说钻进过程中井底压力始终在窄压力窗口内，有效避免了因井筒压力不平衡导致的井下复杂情况。此外，回压实时调节条件下三种最优钻井参数组合的随钻井底压差均小于0.1 MPa。与回压恒定条件下的随钻井底压差相比[11]，回压实时调节条件下的随钻井底压差上限由0.25 MPa下降至0.1 MPa。这是因为井口回压的实时调节使得井筒压力剖面得到进一步优化，进一步最小化了优化模型的目标函数值(即井底压差)。较小的井底压差有利于提高机械钻速，减少储层伤害，降低钻井综合成本。

综上，井口回压实时调节优化模型优化了钻进过程中的井口回压，达到优化井筒压力剖面的效果，可更好地适应窄压力窗口，同时保证了随钻井底压差维持在较小的水平上。利用井口回压实时调节优化模型后不仅增加了最大钻进深度，而且进一步减小了随钻井底压差，有利于储层保护和钻井提速。

图5 回压实时调节条件下的随钻井底压差Fig. 5 The bottom-hole pressure difference under real-time adjustment of backpressure

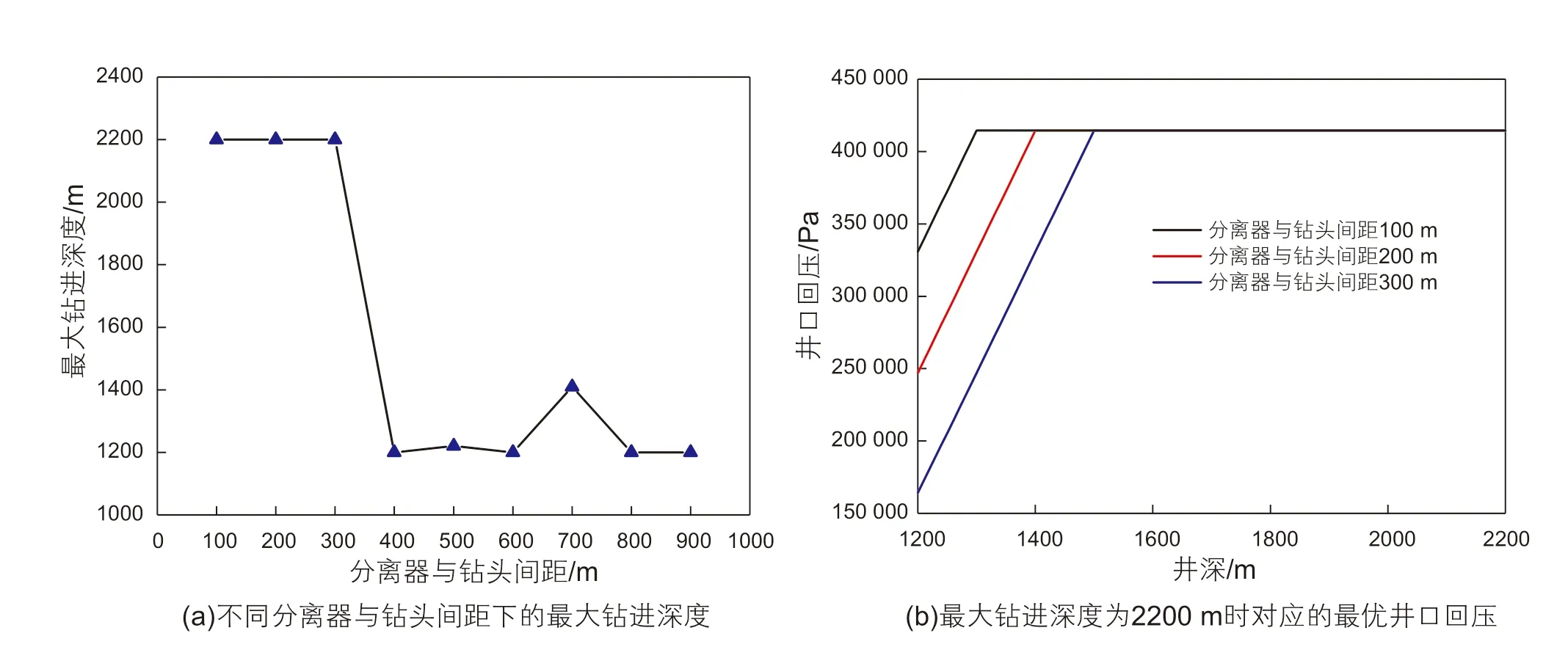
图6 不同分离器与钻头间距下的最大钻进深度和最优井口回压Fig. 6 Maximum drilling depth and optimum wellhead backpressure under different distance between separator and bit

3.2 不同钻井参数对回压优化结果和最大钻进深度的影响

在窄压力窗口为1.03～1.10 g/cm3、分离效率为0.4、分离器与钻头之间距离为500 m、空心球注入体积分数为0.3、纯钻井液密度为1200 kg/m3、排量为40 L/s下，探究了回压实时调节条件下单一变量对最大钻进深度和最优井口回压的影响。

(1)不同分离器与钻头间距下的最大钻进深度和最优井口回压

图6(a)给出了不同分离器与钻头间距下的最大钻进深度，图6(b)给出了最大钻进深度为2200 m时对应的最优井口回压。可以看出，分离器与钻头间距分别为100 m、200 m、300 m时，均可实现最大钻进深度2200 m。此外，三种分离器与钻头间距对应的最优实时井口回压值有所差异，但钻进过程中的井口回压实时调节规律基本相同，均是先升高后保持恒定。可以看出，在井口回压升高阶段，分离器与钻头间距越大，最优井口回压值越小。这是因为对于特定的窄压力窗口而言，分离器与钻头间距越大，重质钻井液在井筒内的占比增加，导致静液柱压力增加，此时需要通过调小井口回压值来保证井筒压力始终位于窄压力窗口内。

(2)不同空心球注入体积分数下的最大钻进深度和最优井口回压

图7(a)给出了不同空心球注入体积分数下的最大钻进深度，图7(b)给出了最大钻进深度为1710 m时对应的最优井口回压。可以看出，空心球注入体积分数为0.25时，可实现最大钻进深度1710 m。此外，最大钻进深度为1710 m时对应的最优井口回压先恒定在2.0×105Pa后升高至5.0×105Pa左右，井口回压实时调节规律简单，可操作性较强。

(3)不同纯钻井液密度下的最大钻进深度和最优井口回压

图8(a)给出了不同纯钻井液密度下的最大钻进深度，图8(b)给出了最大钻进深度为2200 m时对应的最优井口回压。可以看出，纯钻井液密度分别为1100 kg/m3和1150 kg/m3时，均可实现最大钻进深度2200 m。此外，两种纯钻井液密度对应的最优实时井口回压值和调节规律均有差异。差异①：相比于纯钻井液密度为1100 kg/m3时，1150 kg/m3条件下对应的最优井口回压值较小。这是因为对于特定的窄压力窗口而言，钻井液密度的增大使得静液柱压力增加，此时需要通过调小井口回压值来保证井筒压力始终位于窄压力窗口内。差异②：纯钻井液密度为1100 kg/m3时，钻进过程中最优井口回压持续升高，而纯钻井液密度为1150 kg/m3时，最优井口回压先升高后保持恒定。

(4)不同排量下的最大钻进深度和最优井口回压

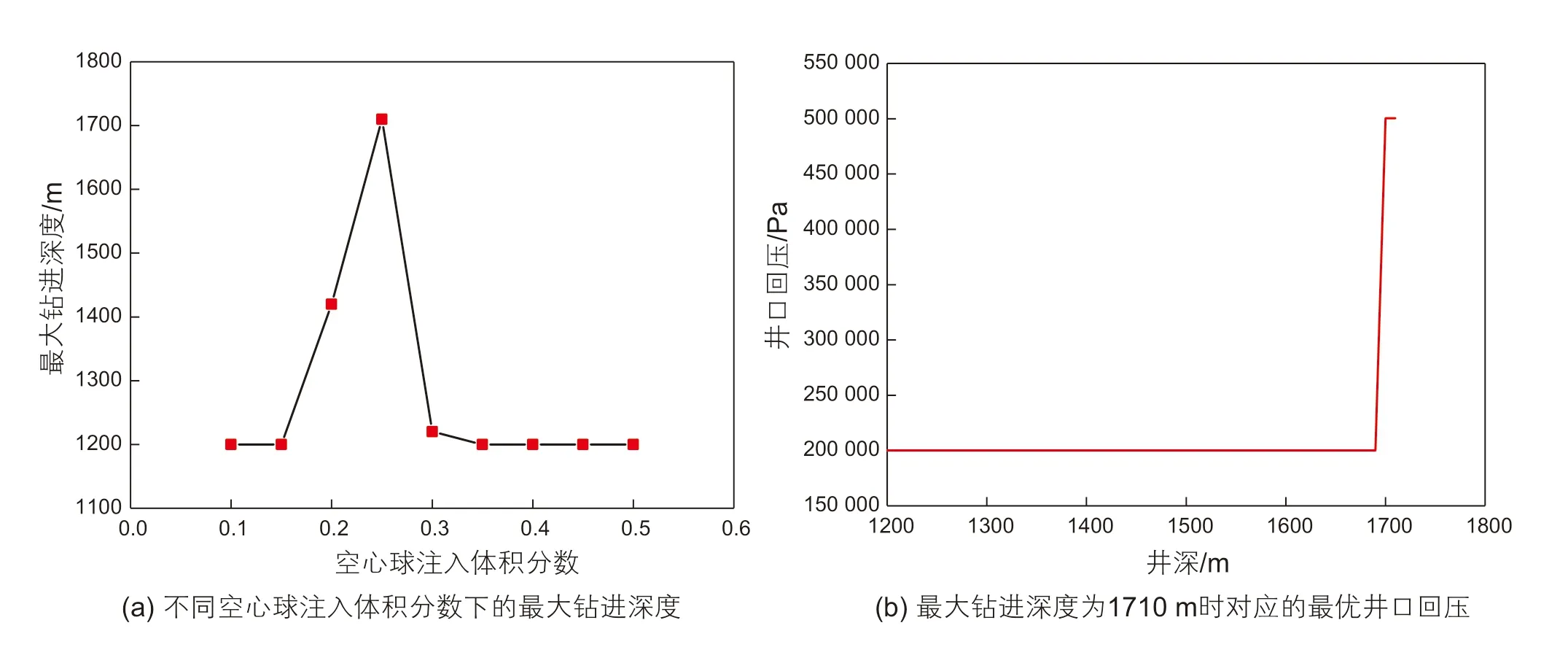
图7 不同空心球注入体积分数下的最大钻进深度和最优井口回压Fig. 7 Maximum drilling depth and optimum wellhead backpressure under different volume fraction of hollow spheres

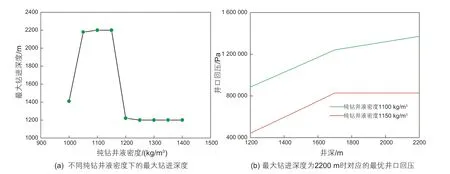
图8 不同纯钻井液密度下的最大钻进深度和最优井口回压Fig. 8 Maximum drilling depth and optimum wellhead backpressure under different density of pure drilling fluid

图9(a)给出了不同排量下的最大钻进深度，图9(b)给出了最大钻进深度为1260 m时对应的最优井口回压。可以看出，排量为25 L/s时，可实现最大钻进深度1260 m。此外，最大钻进深度为1260 m时对应的最优井口回压在钻进过程中呈线性增加。

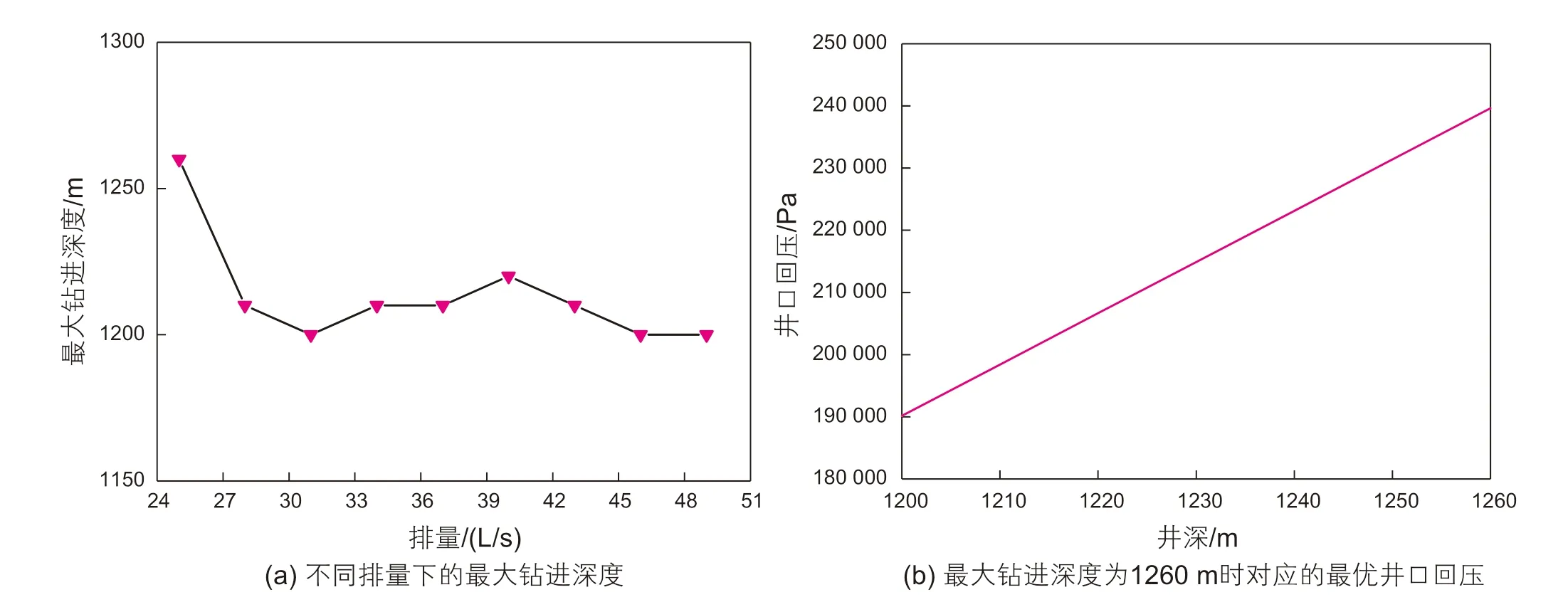
图9 不同排量下的最大钻进深度和最优井口回压Fig. 9 Maximum drilling depth and optimum wellhead backpressure under different displacement

综上，通过探究单一变量变化时的最大钻进深度，可以得出相比于空心球注入体积分数和排量，最大钻进深度受分离器与钻头间距和纯钻井液密度的影响更为明显。这是因为相比于空心球注入体积分数和排量两个因素，分离器与钻头间距和纯钻井液密度的改变对井筒压力剖面的影响更加明显，更有利于获取最优的井筒压力剖面，实现更大的钻进深度。此外，通过分析最优井口回压变化规律，可以得出同一最大钻进深度条件下不同钻井参数值对应的最优井口回压值和井口回压实时调节规律有所差异。