Improvement of X-Band Polarization Radar Melting Layer Recognition by the Bayesian Method and ITS Impact on Hydrometeor Classification
2020-04-01JianliMAZhiqunHUMeilinYANGandSitengLI
Jianli MA, Zhiqun HU, Meilin YANG, and Siteng LI
1Institute of Urban Meteorology, China Meteorological Administration, Beijing 100089, China
2State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081, China
ABSTRACT Using melting layer (ML) and non-melting layer (NML) data observed with the X-band dual linear polarization Doppler weather radar (X-POL) in Shunyi, Beijing, the reflectivity (ZH), differential reflectivity (ZDR), and correlation coefficient (CC) in the ML and NML are obtained in several stable precipitation processes. The prior probability density distributions (PDDs) of the ZH, ZDR and CC are calculated first, and then the probabilities of ZH, ZDR and CC at each radar gate are determined (PBB in the ML and PNB in the NML) by the Bayesian method. When PBB > PNB the gate belongs to the ML, and when PBB < PNB the gate belongs to the NML. The ML identification results with the Bayesian method are contrasted under the conditions of the independent PDDs and joint PDDs of the ZH, ZDR and CC. The results suggest that MLs can be identified effectively, although there are slight differences between the two methods. Because the values of the polarization parameters are similar in light rain and dry snow, it is difficult for the polarization radar to distinguish them.After using the Bayesian method to identify the ML, light rain and dry snow can be effectively separated with the X-POL observed data.
Key words: X-band polarimetric radar, Bayesian method, melting layer identification, hydrometeor classification
1. Introduction
The bright band of the melting layer (BBML) is often observed by weather radar in the precipitation processes of stratiform clouds or mixed-phase stratiform clouds. It is a common phenomenon that is caused by the melting surface of slowly falling ice crystals and snowflakes near the thawing layer at 0°C which forms an obvious ring on the plan position indicator (PPI) for reflectivity (ZH), differential reflectivity (ZDR), and the correlation coefficient (CC). Below the BBML, ice crystals and snowflakes melt into raindrops, the size of the particles decreases, the falling speed increases,and the concentration decreases at the same time. As a result, ZHdecreases. Therefore, the 0°C layer is also known as the melting layer (ML), accompanied by a bright band in radar observations. The height of the zero-degree layer can be estimated according to the BBML observed with radar,and the stability of the atmosphere can be further verified. Before the emergence of polarization radar, bright band detection was mainly based on the ZH, which was used for bright band identification and correction. For example, Smith(1986) used the statistical characteristic curve of the bright band ZHto identify the BBML. Kitchen et al. (1994) applied the method of vertical profile reflectivity (VPR) to identify the BBML and developed an algorithm for bright band correction. Sánchez-Diezma et al. (2000) developed a set of algorithms for automatically identifying the peak density and thickness of the BBML with simulated radar data. Subsequently, White and Daniel (2002) combined weather radar and wind profilers to identify the BBML, yielding more accurate identification results than with VPR only.Zhang et al., (2008), Zhang and Qi, (2010) successively utilized the mean vertical profile of reflectivity (MVPR) and apparent vertical profile of reflectivity (AVPR) methods to identify and modify the BBML and test the algorithm in weather processes. On the basis of Zhang et al. (2008),Zhang et al. (2010) improved the incorrect recognition of stratiform and convective clouds and further enhanced the accuracy of BBML recognition by VPR. Xiao et al. (2010) developed an automatic BBML recognition and elimination algorithm based on the average VPR for the China new generation Doppler weather radar (CINRAD). Using the vertical beam of the L-band wind profile radar, Huang et al. (2011,2013, 2015) studied BBML identification in the Beijing area according to the echo change rate and the velocity of particles falling from the ML. Zhuang et al. (2013) used the VPR to study the identification of the BBML over the Qinghai-Xizang Plateau and noted that the error in the radar precipitation estimation was significantly reduced after the correction of the bright band. Based on stratiform and convective cloud classification, Sun (2014) corrected the BBML by the AVPR method and verified it by quantitative precipitation estimation (QPE). After comparing the three algorithms for identifying the BBML, Cao et al. (2018) noted that the QPE result using the BBML correction by AVPR and by the apparent vertical profile of the CC is better than that by the MVPR method. Giangrande et al. (2008) developed an algorithm for identification of the BBML based on polarimetric parameters and successfully applied it to the WSR-88D polarization radar in the United States.
The X-band dual linear polarimetric doppler weather radar (hereafter referred to as X-POL) has received much attention in recent years and been applied as a useful supplement to operational radars. Because the polarization signatures of melting snowflakes are obviously different from those of raindrops and the wave scattering at the X-band is a non-Rayleigh scattering regime, X-POL is more sensitive to the characteristics of the BBML. Traditional methods often use the profile of polarimetric parameters to identify the BBML, such as VPR, VPDR (vertical profile differential reflectivity), and the VPC (vertical profile correlation coefficient). There are few algorithms for BBML recognition using X-POL in China. In this paper, the Bayesian method is developed and applied for X-POL to identify the BBML in Beijing.
Following this introduction, section 2 illustrates the specification, distribution and data credibility of X-POL. The data processing, images and statistical characteristics in the bright band of ZH, ZDRand CC observed by X-POL are described in section 3. The principles and steps of ML identification by the Bayesian method are presented in detail in section 4, which includes how to utilize the independent probability density distribution (IPDD) and joint probability density distribution (JPDD) of ZH, ZDRand CC to improve ML identification. Using the presented method, in section 5, a weather process that embodies the BBML is analyzed to verify the identification result. In section 6, the improvements in hydrometeor classification with the BBML detection are assessed. Finally, in section 7, a summary and some discussion of the Bayesian method for X-POL ML identification are provided.
2. Illustration of the X-POL network
To strengthen the monitoring of disastrous weather and compensate for the deficiency of CINRAD/SA Doppler weather radars in low-altitude detection, five new X-POLs were built in the Beijing area in 2016 for the monitoring and early warning of disastrous weather. The spatial distribution of the five radars is shown in Fig. 1, in which the solid circles represent the detection ranges (60 km) of the XPOLs. The basic radar performance parameters are shown in Table 1. The volume scans are composed of nine elevation angle scans ranging from 0.5° to approximately 19.5° according to a standard WSR-88D scanning strategy (VCP21 mode), but the volume scan period is three minutes. The detection parameters include ZH, radial velocity (Vr), velocity spectrum width (Sw), ZDR, CC, and propagation phase shift(ФDP). The data for the bright band analysis are from XPOL in 2018 in Shunyi, Beijing.
The data are preprocessed by attenuation correction and de-noised by wavelet analysis (Hu et al., 2010; Hu and Liu,2014), and the processing methods are briefly described in the following subsections.
2.1. Attenuation correction
The attenuation effect on radar ZHand ZDRat the Xband is substantial and cannot be ignored. The path-integral attenuations are compensated for by adding the attenuation to the measured ZHand ZDRas follows:
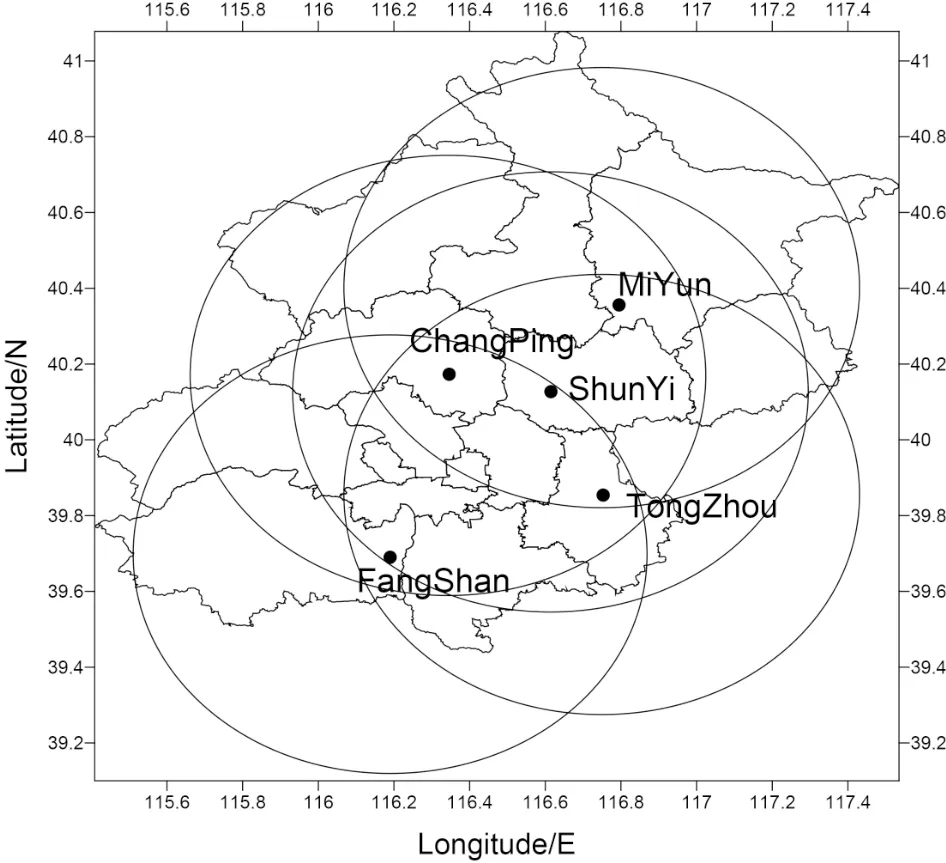
Fig. 1. The distribution of Beijing X-POLs, where the circles indicate the radar detection ranges of the X-POLs (60 km).
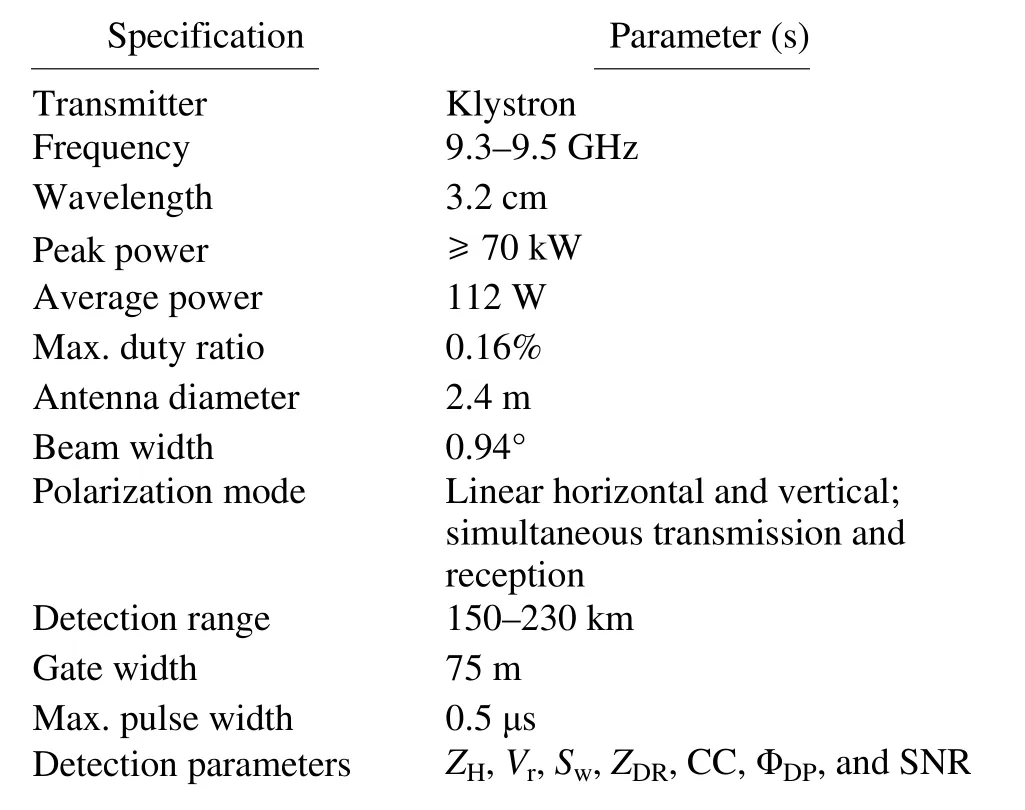
Table 1. The main performance parameters of X-POL.
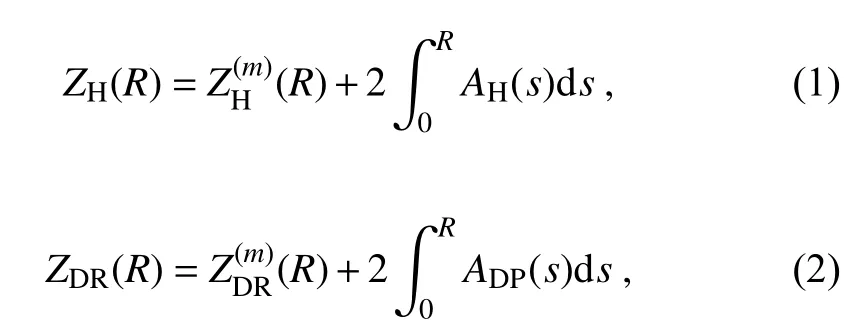

where Zh= 1 0ZH/10, and the parameters in the formulas are set as: α = 1.37 × 10-4dB km-1(mm6m-3)-1; β = 0.779; d =1.13; γ = 0.14; σ1= 0.2 deg km-1and σ2= 4.0 deg km-1; and a1= 0.22 dB deg-1and a2= 0.033 dB deg-1.
2.2. Wavelet de-noising
The random fluctuation is reduced using wavelet de-noising with the following steps: (1) Deconstruction: each radial data is deconstructed into five levels with a db5 wavelet function. (2) De-noising: the detail coefficients in each level are suppressed with a ФDPpenalty strategy. (3) Reconstruction: the data are reconstructed by means of an approximation and the processed detail coefficients with a soft function scheme. Once the data have been processed with the aforementioned attenuation correction and denoising, they are analyzed for BBML identification, as described in the following sections.
2.3. Data reliability
According to the physical meaning of ZDR, the ZDRvalue in light rain should be approximately equal to zero. In order to verify the reliability of ZDR, some light rain data are selected in three precipitation processes. The criteria for light rain echoes are: signal to noise ratio (SNR) > 20 dB;slant range between 10 km and 20 km away from the radar;ZH< 15 dBZ; and CC > 0.98. After finding the gates that meet the light rain criteria, and averaging these gates of ZDR, SNR and CC, the maximum average value of ZDRis 0.12 dB and the minimum is 0.06 dB, as shown in Table 2.All the average values of ZDRare close to zero, which indicates there is almost no systematic deviation in the ZDRvalue.
3. Bright band signature of X-POL observations
A wide range of stratiform precipitation occurred in Beijing on 30 August 2018, and obvious signatures of the BBML were observed with all five X-POLs in Beijing. Figure 2 shows the attenuation-corrected ZH, ZDRand CC in a PPI of 9.9° observed with the Shunyi X-POL at 0030 UTC,where the outermost circle is 60 km (the same below). Because the dielectric constant of water is greater than that of ice, the dielectric constant increases significantly as ice crystals or snowflakes start to melt when temperature is above zero degrees. This forms rings in the PPI, which consist of the larger values of ZHand ZDR, and the smaller value of CC. As there are four lightning-protection rods around the radar, an obvious “cross” shape in the PPI of the ZDRis observed because the value of the ZDRis significantly increased near the azimuths of the rod locations. Therefore,the data affected by the lightning rods will be discarded when obtaining the statistical characteristics of ZH, ZDRand CC for the bright band in section 4.2.
As a reminder, the partial criteria of Giangrande et al.(2008) for designation of ML boundaries is: the heights that encompass a majority of the ML points are determined. In the proposed algorithm, the ML top is determined as the height below which 80% of ML points reside. Similarly, the ML bottom is determined as the height below which 20% of the ML points reside. This algorithm is referred to as the MLDA (melting layer detection algorithm). The wavelength of the X-band radar is smaller than that of the S-band, so Xband radar is prone to non-Rayleigh scattering. When particles, such as wet snow with large diameters, are in the non-Rayleigh scattering regime, the electrical size of theparticles is larger at the X-band than that at the S-band,which leads to a stronger non-Rayleigh scattering effect for the X-band radar observations. The larger differential scattering phase yields the reduced correlation of the dual polarization signals, leading to obvious differences in the values of ZH, ZDRand CC observed in the BBML from these at the Sband. The ZHvalues are distributed from 20 to 30 dBZ within the bright band region in azimuths from 120° to 150°(Fig. 2). There are obvious errors when determining the BBML points by using the MLDA algorithm based on the S-band WSR-88D ZH[ZH∈ (30, 47) dBZ], which is not applicable to identifying BBML with X-POL measurements.In other words, most of the values are smaller than 0.90 in the PPI of the CC. This is also quite different from the values of the BBML points [CC ∈ (0.90, 0.97)] identified by the S-band WSR-88D. Therefore, it is necessary to redefine the distribution range of the BBML points using the bright band data observed with X-POL. According to the data from the slant ranges from 10 to 30 km in Fig. 2, the distributions of ZH, ZDRand CC are calculated and shown in Fig. 3.As seen from Fig. 3, most of the CC values are above 0.98 in the rain region from approximately 10 to 20 km. When the slant ranges are approximately from 20 to 22.5 km,which approaches the BBML, the CC values begin to decrease, and the minimum can reach 0.7. Therefore, the slant range of the BBML is roughly located from 20 to 25 km,where the CC values are mainly distributed from 0.70 to 0.96. The CC values increase gradually from 22.5 to 25 km and are mostly above 0.96 in the dry snow region, where the slant range is approximately 25 to 30 km.
ZHand ZDRare consistent with the characteristics of the BBML; both first increase and then decrease in the range of the BBML from 20 to 25 km, where the values of ZHare mainly distributed from 15 to 46 dBZ and those of the ZDRare from -0.2 to 3.0 dB. However, the values of the ZDRare from 0.80 to 2.5 dB for WSR-88D. Therefore, the X-POL parameter thresholds are different from those of the WSR-88D polarimetric radar. Although the values of the polarimetric parameters in the BBML are mainly distributed within a certain scope, they are more reasonable after statistical processing because the boundary is not completely determined.
4. BBML identification step
4.1. BBML identification principle based on the Bayesian method
The Bayesian method can be used to identify the ML if the distributions of the probability densities of the ZH, ZDRand CC in the ML region are known in advance. The steps of BBML identification are described as follows (Zhang,2016): The radar echoes are divided into two categories, C =(BB, NB), in which the ML echo is represented by BB and the non-melting layer (NML) echo is represented by NB.The identification vector, y = (ZH, ZDR, CC), is determined by combining the polarimetric parameters of ZH, ZDRand CC. The variable y belongs to BB only when p(BB| y) is larger than p(NB| y), where p represents the probability density. According to Bayesian theory (Papoulis, 1991),

Fig. 2. The PPIs of (a) ZH, (b) ZDR, and (c) CC of X-POL in 9.9° at 0030 UTC 30 August 2018, in Shunyi, Beijing.

Fig. 3. Distributions of (a) ZH, (b) ZDR and (c) CC corresponding to Fig. 2.
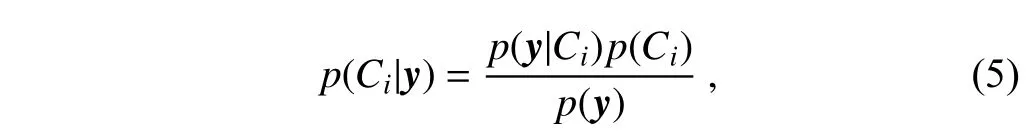
where Ci= (BB, NB), and p( y) = K represents the probability of observing the discriminant factor, assuming that it is the same as the classification probabilities for BB and NB(i.e., p(BB) = p(NB) = 1/2). Thus, p(Ci| y) is proportional to p( y|Ci)p(Ci), and Eq. (5) is transformed into:

Based on the assumption that the classification is independent in a simple Bayesian identification, the conditional probability density can be decomposed into:
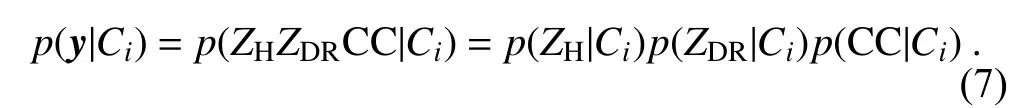
If it is assumed that the distribution of parameters in the observed discriminant vector y= (ZH, ZDR, CC) is not independent, the joint probability is used to determine whether y belongs to the ML. Then, the conditional probability density can be decomposed into:
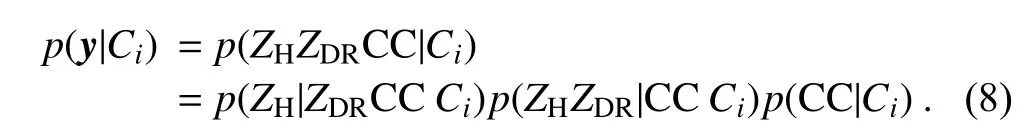
4.2. Obtaining the prior probability distribution
To obtain the probability density distributions (PDDs)of the ZH, ZDR, and CC in the BBML, the ML data observed by Shunyi X-POL shown in Table 3 are analyzed,and their prior PDDs are acquired according to the characteristic values of the X-POL in the ML. There are 634 volume scan data that include the BBML in eight days, observed by the VCP21 model, which scans one volume every three minutes. The ML region is manually selected from the 9.9°PPI, and the data influenced by lightning rods are excluded.A total of 6 705 261 sets of data are identified as ML points,and 85 368 196 sets of data are identified as NML points in the PPI. Based on these data, the IPDDs of the ZH, ZDRand CC are shown in Fig. 4, where BB represents the ML and NB represents the NML. Figure 4 shows that the IPDDs of the ZH, ZDRand CC for BB are greater than zero for approximately ZH∈ (5, 46) dBZ, ZDR∈ (-0.30, 3.5) dB, and CC ∈(0.75, 0.96). It can be seen from the diagram that the PDDs of ZHand CC in the ML and NML are quite different, which is very beneficial for distinguishing the BB from the NB.
The peak value of p(CC|BB) is located at CC = 0.93,which is obviously smaller than that of p(CC|NB) (approximately 0.98). The PDDs of the ZHand ZDRin the ML and NML partially overlap, but the ZHand ZDRvalues of the BBML are larger than those of the NML. Therefore, the PDD, combined with the ZH, ZDRand CC, can provide more information to distinguish the BB from the NB. Figure 5 shows the JPDDs of the ZH, ZDRand CC in the ML and NML, in which the differences in the JPDDs between the ML and NML are obvious and benefit distinguishing the BB from the NB.
4.3. Singular point elimination
Because of the influence of ground clutter, some singularity points that are obviously non-melting points are often identified in the near surface by the above method, and these singularities need to be eliminated. The consistency check of the BBML identified by the Bayesian method is carried out to remove the singularity points that deviate from the center of the bright band thickness. The method of singularity elimination using the probability distribution is described as follows:
The point value of (ZH, ZDR, CC) is substituted into Eq.(7) or Eq. (8), and the probabilities of BB and NB are obtained to determine whether the point is in the ML or NMLby contrast with the PDDs in Figs. 4 and 5.
Table 3. Melting layer data observed by Shunyi X-POL.
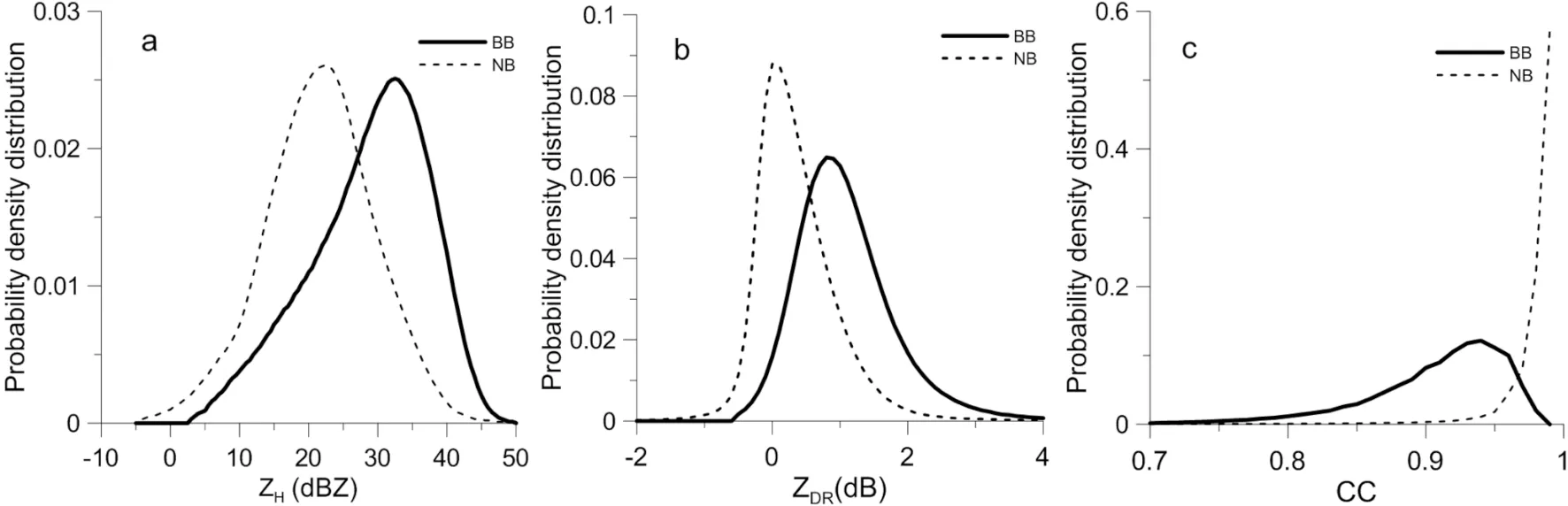
Fig. 4. The IPDDs of the ZH, ZDR and CC in the ML and NML.
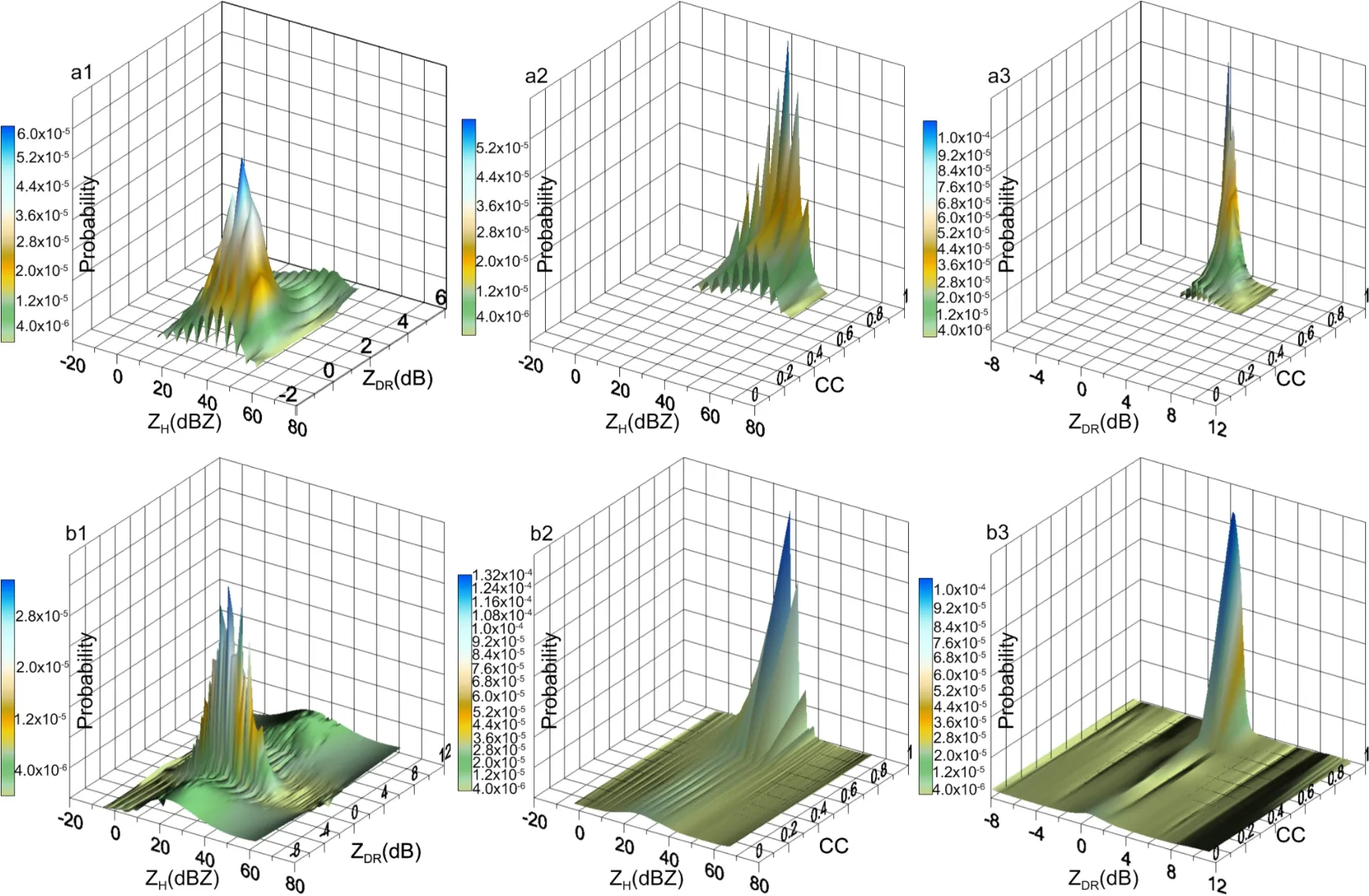
Fig. 5. The JPDD three-dimensional surface data map of (a1) ZH-ZDR, (a2) ZH-CC and (a3) ZDR-CC for BB. (b1-b3)As in (a1-a3) but for NB.
The upward float is 20% towards the height of the temporary bottom and the downward float is 20% towards the height of the temporary top according to all of the BBML points identified by step (1) in a certain PPI of the polarization radar, and the temporary thickness of each azimuth is obtained from the temporary bottom and top heights.
The median value, h, is calculated by sorting the results of the temporary thickness at each azimuth. Let σ = 2h;then, reidentify the BBML points in step (1) in the area determined by
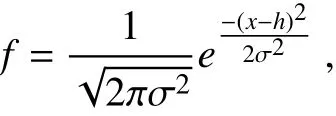
where x is the height corresponding to each gate and f is the probability of a normal distribution.
5. Case analyses
To verify the effect of BBML identification by the Bayesian method, the independent dataset from the Shunyi radar on 11 July 2018 is used for testing.
Figure 6 shows the 9.9° PPI, which includes the BBML observed at 0500 UTC 11 July 2018 (unless specified, the following times and elevation angles are the same). Figure 6a shows the ZHand Figure. 6b shows the CC. The black color in Fig. 6c represents the result of the BBML recognition by the Bayesian method according to the IPDD, and the black color in Fig. 6e is according to the JPDD. It can be seen from Fig. 6 that the black rings identified as the BBML are very consistent with the decreasing CC region regardless of whether the ZH, ZDRand CC are based on the IPDD [Eq.(7)] or the JPDD [Eq. (8)] in the Bayesian method.
In the area far away from the BBML and near the radar station in Figs. 6c and e, there are points that are obviously mistakenly identified as the BBML due to ground clutter interference. There are more error recognition points in Fig. 6c than in Fig. 6e near the radar station, which indicates that the JPDD is better than the IPDD in suppressing the false recognition of ground clutter as ML points. The main reason is that the value of the CC is small, but the ZHand ZDRincrease or decrease at the same time in the BBML; the CC value of ground clutter is also small, however the changes in the ZHand ZDRvalues are random. A consistency check is carried out on the BBML identified by the Bayesian method to remove the singularity points that deviate from the center of the bright band. Figures 6d and f show the results of eliminating singularity points corresponding to Figs. 6c and e, respectively. After eliminating the singularity points,there is a slight difference between Figs. 6d and f, but they are almost the same. The results of BBML identification are very consistent with the reduction band of the CC value in the PPI, which shows that both Bayesian methods, i.e., using IPDDs and JPDDs of (ZH, ZDR, CC), can effectively identify the BBML.
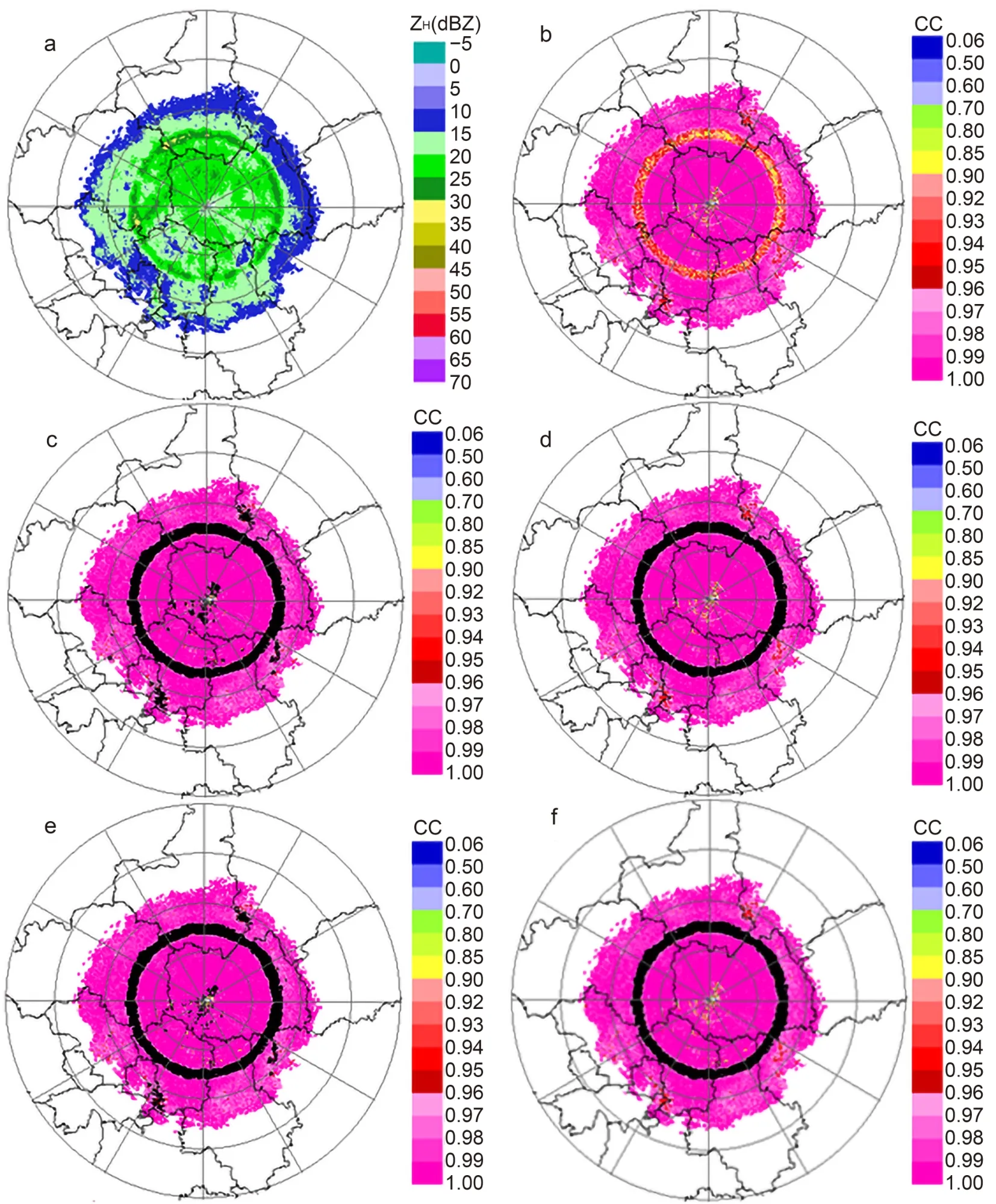
Fig. 6. The PPIs of (a) ZH and (b) CC in 9.9° at 0500 UTC 11 July 2018 (unless specified, the following times and elevation angles are the same). The BBML points are shown in black according to the (c) IPDD and (e) JPDD. Panels (d, f) correspond to (c, e) after singular point elimination, respectively.
The bottom height of the zero-degrees layer is approximately 4600 m, and the top height is approximately 5000 m according to the sounding at 0600 UTC 11 July 2018. Figure 7 shows the ML height identified using the 9.9° PPI by the Bayesian method at 0415 UTC 11 July 2018, where Fig. 7a shows the IPDD result and Fig. 7b the JPDD result. In the figure, ML-Bot indicates the recognized ML bottom height,and ML-Top indicates the corresponding top height. Sou-Top and Sou-Bot are the heights of 0°C and 2.5°C obtained by sounding, respectively. There are slight differences between Figs. 7a and b, but the overall trend is consistent.The mean values of the bottom and top heights are 4590 m and 5009 m in Fig. 7a and 4575 m and 5027 m in Fig. 7b, respectively, which indicates that the performances of the two methods are similar.
For the MLDA of WSR-88D, the gate is considered as the BBML point when the values of ZH, ZDRand CC are ZH∈ (30, 47) dBZ, ZDR∈ (0.80, 2.5) dB, and CC ∈ (0.90,0.97), respectively. As shown in Fig. 8c, the black color represents the recognized melting points by this MLDA, which are very limited. In the BBML of X-POL, most of the values of ZHare less than 30 dBZ, and the CC is less than 0.9,which do not satisfy the conditions of the ZH, ZDRand CC of the MLDA. Therefore, only a very small number of points are identified in the ML. This is mainly due to different scattering types between the X-band radar and S-band radar in the ML; X-band radar mainly results in Mie scattering, while S-band radar mainly results in Rayleigh scattering. Different scattering types lead to the ZHof the X-band being smaller than that of the S-band radar, but the ZDRof the X-band being larger than that of the S-band when the Xband and S-band radars detect wet snow in the same area.The scattering phase of the X-band radar is larger than that of the S-band radar, which makes the CC of the X-band radar smaller than that from the S-band radar. Therefore, the identification parameters for ML are different between the X-band and S-band radars.

Fig. 7. Bottom and top heights of the BBML identified by the Bayesian method with the (a) IPDD and (b)JPDD.
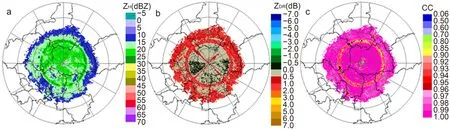
Fig. 8. The PPIs of (a) ZH, (b) ZDR and (c) CC in 9.9° at 0500 UTC 11 July 2018. The BBML points identified according to the MLDA of WSR-88D are shown in black in Fig. 8c.
According to the idea of the MLDA, with X-POL radar parameters of ZH∈ (5, 46) dBZ, ZDR∈ (-0.30, 3.5) dB,and CC ∈ (0.75, 0.96), the ML is reidentified. After finding the ML points, the ML top is determined as the height below which 80% of ML points reside, and the ML bottom is determined as the height below which 20% of the ML points reside. The black ring in Fig. 9a represents the BBML identified after the parameters are adjusted to XPOL. Figure 9b shows the results of the remaining points after limiting 20% and 80% of the BBML in Fig. 9a, and Fig. 9c shows the height of the BBML in each azimuth in Fig. 9b. It can be seen from Fig. 9c that some bottom heights of the BBML are lower than 1 km. Obviously, most of these points result from ground clutter, which has a great influence on BBML identification. In particular, the height of the ML top is obviously overestimated in azimuths from 203° to 209°.
The asymmetric or partial BBML in PPI images is selected to further verify the effect of the Bayesian method in identifying the ML. A case of asymmetric or partial BBML is displayed in Fig. 10, which shows the Fangshan radar of 9.9° PPI at 0130 UTC 11 July 2018. It can be seen from Fig. 10 that the BBML points identified by IPDD and JPDD correspond well to the ML area where the CC decreases. The result of Fig. 10 indicates that the Bayesian method can also effectively identify the asymmetric or partial BBML in the PPI.
6. Hydrometeor classification improvements
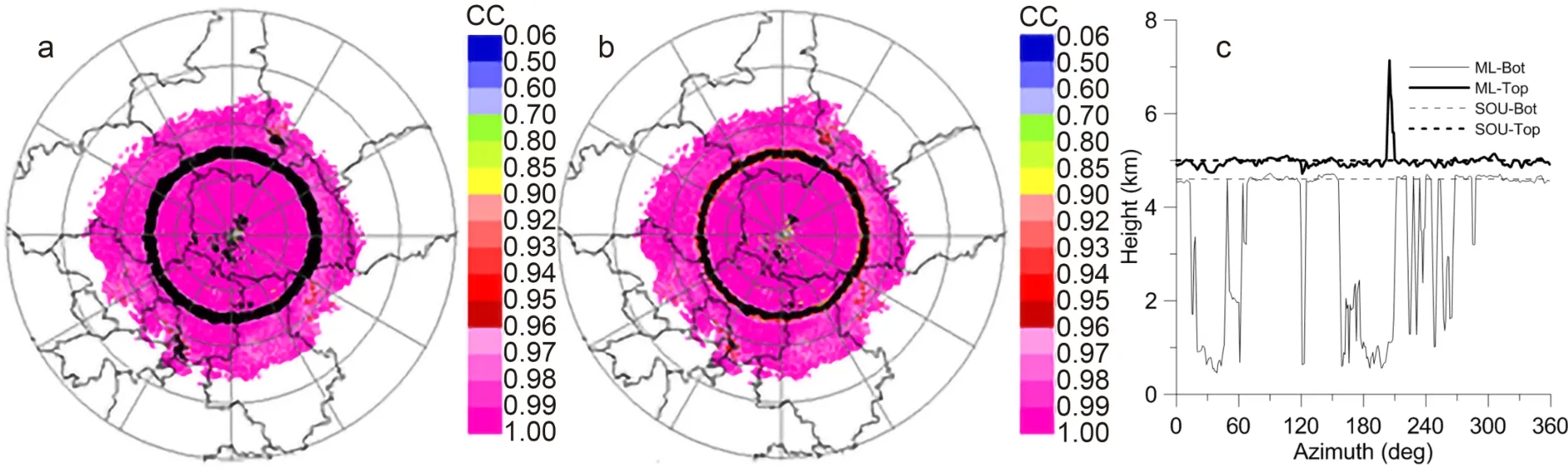
Fig. 9. BBML detection after the parameters are adjusted to X-POL (a), the results of the remaining parameters after limiting 20% and 80% of the BBML (b), and the height of the BBML in each azimuth (c).
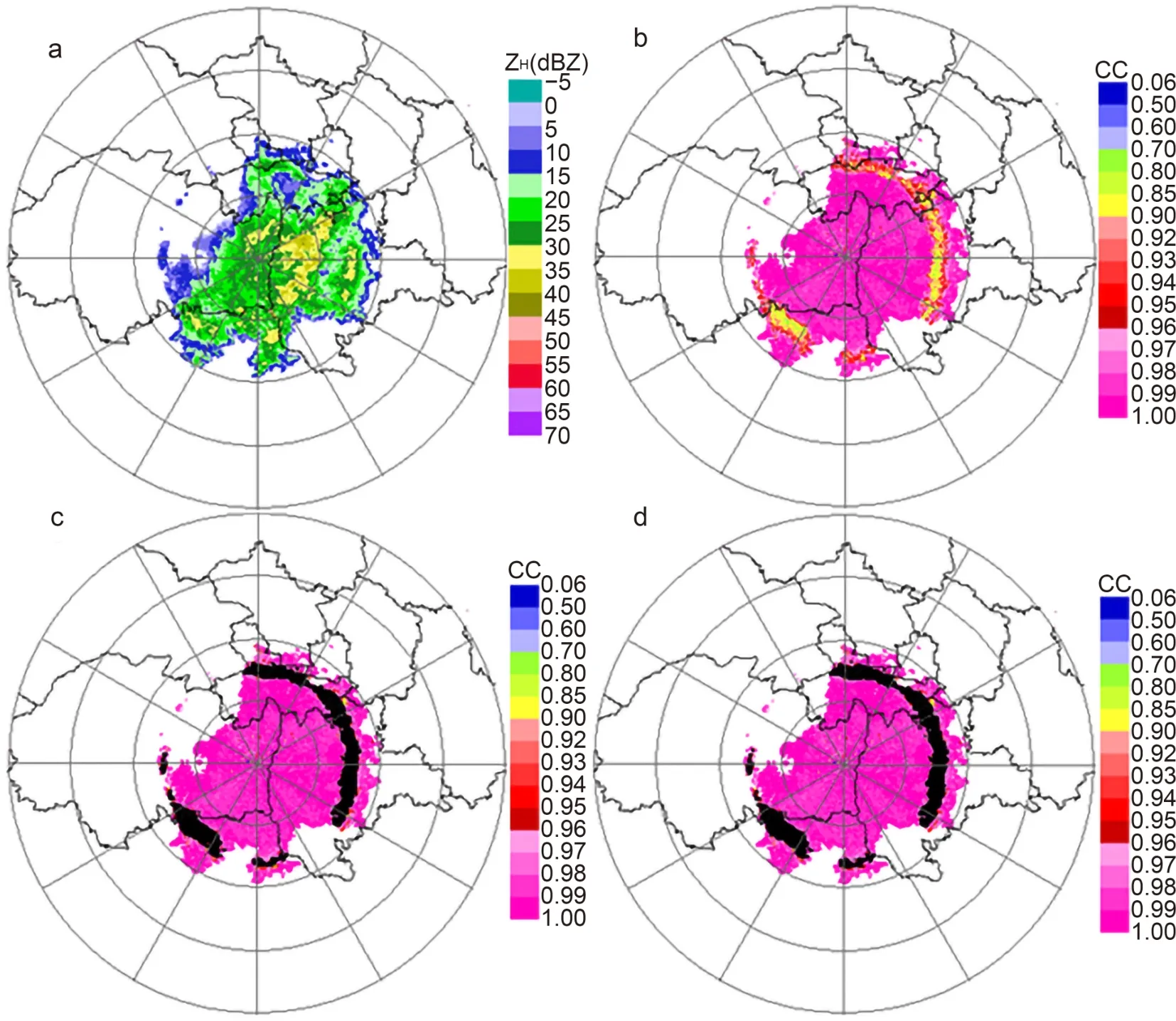
Fig. 10. The ZH (a), CC (b), and the BBML points (shown in black) according to the IPDD (c) and JPDD (d)of X-POL in 9.9° PPI at 0130 UTC 11 July 2018, in Fangshan, Beijing.
The extents of the polarization parameter values of ZH,ZDRand CC overlap for dry snow and light rain. Figure 11 shows the PDD characteristics of light rain and dry snow in the 9.9° PPI at 0500 UTC 11 July 2018. Most of their PDDs overlap; thus, it is very difficult to use the fuzzy logic algorithm to distinguish dry snow and light rain. Therefore, it is very important to recognize the BBML because dry snow cannot appear under the BBML (Rbbin Fig. 12), and light rain should not appear above the BBML (Rttin Fig. 12). Figure 12 shows the intersection between beam broadening and the BBML. The heavy line represents the center of the radar beam at a 9.9° elevation angle, and the dashed line represents the ±0.5° beam width (3 dB beam width). Rbb, Rb, Rtand Rttrepresent the slant ranges corresponding to the intersection points between the radar beam and the BBML; and Hband Htrepresent the heights of the bottom and top of the BBML, respectively.
The hydrometeor particles are classified according to Table 4. Based on the distribution constraint relations of hydrometeor particles (Park et al., 2009), for a weather process in the BBML, the relationship between hydrometeor particles and the ML is as follows (R represents the slant range):
0 < R < Rbb: the particles should not belong to dry snow, wet snow, ice crystals, or graupel;
Rbb< R < Rb: the particles should not belong to dry snow, ice crystals, light to medium rain, or heavy rain;
Rb< R < Rt: the particles should not belong to ice crystals, light to medium rain, or heavy rain;

Fig. 11. The IPDDs of (a) ZH, (b) ZDR and (c) CC for light rain and dry snow.
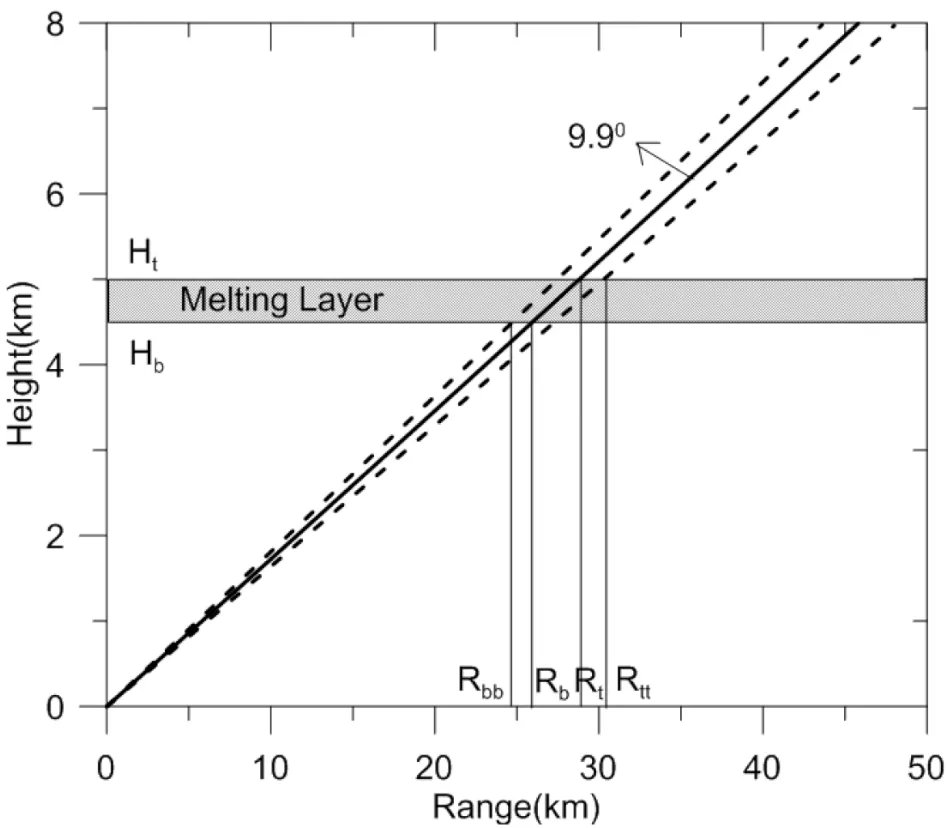
Fig. 12. Sketch of the intersection between beam broadening and the BBML. The heavy line represents the center of the radar beam at a 9.9° elevation angle, and the dashed line represents the ±0.5° beam width (3 dB beam width). Rbb, Rb, Rt and Rtt represent the slant range corresponding to the intersection points between the radar beam and the BBML; Hb and Ht represent the heights of the bottom and top of the BBML, respectively.
Rt< R < Rtt: the particles should not belong to light to medium rain or heavy rain;
R > Rtt: the particles should not belong to ground clutter or abnormal propagation (e.g., hyper-refraction), biological scatter, wet snow, big drops, light to medium rain, or heavy rain.
Without the ML detection, when the slant range is R <Rbb, it is very difficult to distinguish light rain from dry snow by the fuzzy logic algorithm (Fig. 13a). Figure 13a shows the classification identification results, revealing obvious mistakes insofar as the dry snow appears below the BBML. After the BBML is identified by the Bayesian method, according to the constraint relation of the precipitation particle distribution above the BBML, there is light to moderate rain (mainly light rain) in the slant range of R < Rbb(Fig.13b). In the BBML area, wet snow is identified as the main precipitation type, and the type distribution is reasonable,which improves the results of precipitation particle classification by the fuzzy logic method effectively.
In order to further verify the influence of ML recognition on hydrometeors, the results of hydrometeor classification in Fig. 10 are shown in Fig. 14, which also show that the identification of BBML can improve the hydrometeor classification results of light rain and dry snow.
7. Discussion
Based on analysis of ML data observed for eight days with the X-band polarization radar in Shunyi, Beijing, the prior IPDDs and JPDDs of the ZH, ZDRand CC by X-POL areobtained in melting and non-melting regions. The Bayesian method is tested on the 9.9° PPI data at 0500 UTC 11 July 2018, and the abilities of BBML identification are compared under the conditions of the IPDD and JPDD. It is concluded that using both PDDs can improve BBML identification, and the obtained ML height is close to that of the zerodegrees layer in the sounding.
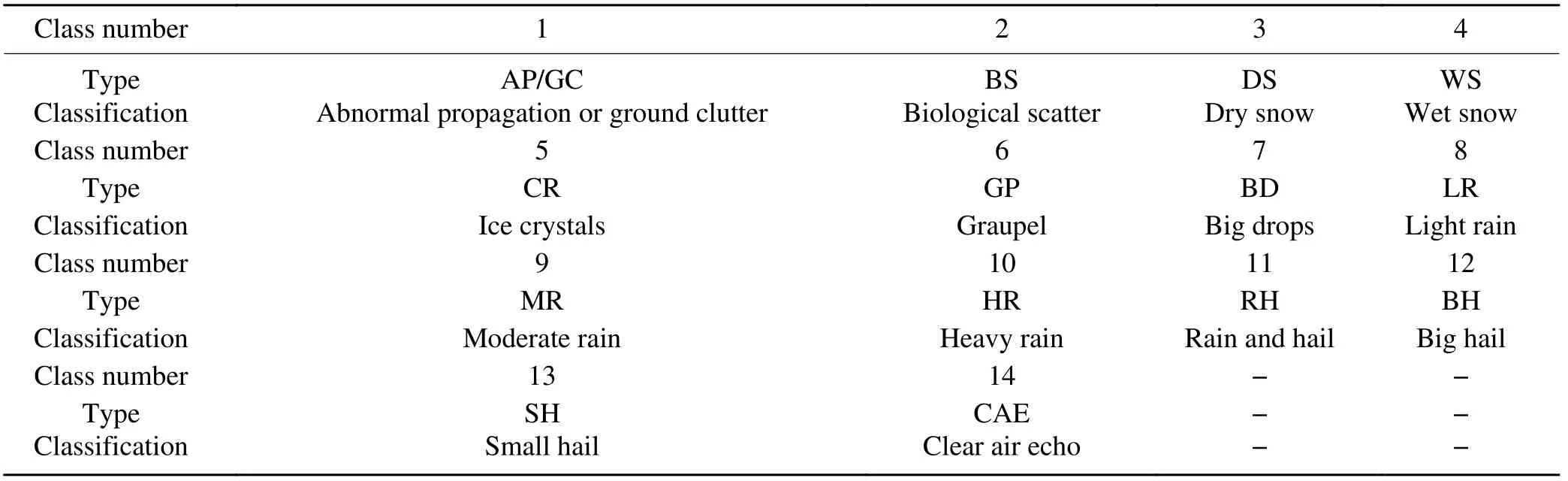
Table 4. Hydrometeor particle-type classification.
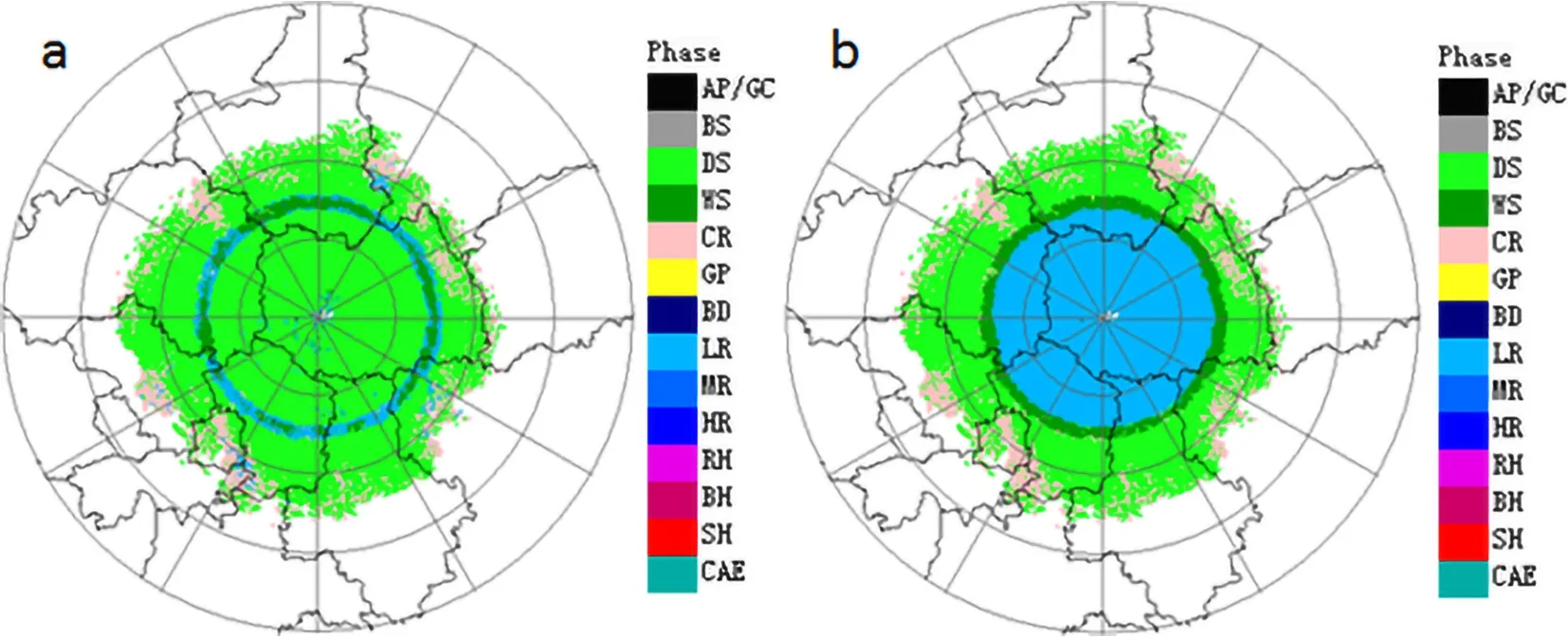
Fig. 13. Hydrometeor classification before (a) and after (b) BBML identification.
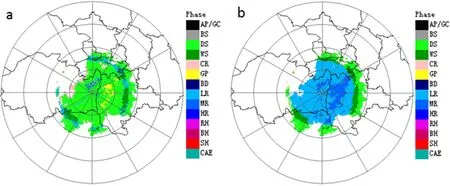
Fig. 14. Hydrometeor classification results in 9.9° PPI at 0130 UTC 11 July 2018 in Fangshan, Beijing,before (a) and after (b) BBML identification.
According to BBML identification by the data collected with the X-POL radar in Shunyi, Beijing, it is shown that the parameter ranges of the ML identification method are ZH∈ (5, 46) dBZ, ZDR∈ (-0.30, 3.5) dB, and CC ∈(0.75, 0.96). However, the parameter ranges for the WSR-88D ML detection method are ZH∈ (30, 47) dBZ, ZDR∈(0.80, 2.5) dB, and CC ∈ (0.90, 0.97). These parameter thresholds are significantly different from those of X-POL and cannot be simply applied to X-POL radars.
The case analysis shows that the Bayesian method can identify the BBML effectively, which plays an important role in hydrometeor classification. Because of the overlapping polarization parameters, it is difficult to distinguish dry snow from light rain using the fuzzy logic algorithm.However, the constraint relationship between dry snow,light rain, and the position of the ML provides much easier mutual identification.
Acknowledgements.This work was supported by a Beijing Municipal Science and Technology Project (Grant No.Z171100004417008), the National Key R&D Program of China(Grant No. 2018YFF0300102), and the National Natural Science Foundation of China (Grant Nos. 41375038 and 41575050).
杂志排行
Advances in Atmospheric Sciences的其它文章
- Constraining the Emergent Constraints
- Simulations of Microphysics and Precipitation in a Stratiform Cloud Case over Northern China:Comparison of Two Microphysics Schemes
- Non-Gaussian Lagrangian Stochastic Model for Wind Field Simulation in the Surface Layer
- Wave-Breaking Features of Blocking over Central Siberia and Its Impacts on the Precipitation Trend over Southeastern Lake Baikal
- A Hybrid Statistical-Dynamical Downscaling of Air Temperature over Scandinavia Using the WRF Model
- Modeling Arctic Boundary Layer Cloud Streets at Grey-zone Resolutions
