基于预计算的高精度可见性及压缩编码

程雯靓

（四川大学计算机学院，成都610065）

0 引言

近年来，计算机图形学被广泛应用于电子游戏、虚拟现实、动画和电影等领域。随着渲染技术及硬件的发展，人们对渲染画面的真实感有了更高的追求。渲染画面的真实感与符合现实世界的物理规律的渲染技术紧密相关，例如基于光线跟踪的全局光照算法等。在为现实世界的物理规律建模的几项要素中，可见性代表了模型几何表面之间的遮挡关系，它使渲染画面具备立体感，是渲染画面具备真实感中不可或缺的一项。然而，可见性与方向相关，每个着色点的可见性需要在其以法线为中心的半球（下文称为法线半球）的各个方向上进行成百上千次的采样并判断该方向是否可见，具有较大的计算量。

在动画、电影等离线渲染领域，其主要目标是为观众呈现生动逼真的画面，对渲染时间没有要求，因此它们更多地使用基于物理的渲染技术，其中的可见性也能被正确计算；而在电子游戏、虚拟现实等领域，不仅追求渲染画面的真实感，也对其实时性有着很高的要求。因为在这些应用中，渲染画面只是其中的一部分，游戏逻辑判断、运动物体的物理碰撞检测等也包含其中，而这些需要在很短的时间内完成，才能带给玩家流畅的游戏体验。因此，这类应用通常会采用近似符合物理规律或基于预计算的渲染技术，以保证渲染画面的真实感及实时性。其中，可见性由于其计算量较大，难以实时计算；并且，可见性与方向相关，每个着色点的可见性大不相同，如果存储可见性信息，将会占据非常大的存储空间。因此，可见性在光照计算中常被省略，导致最终的光照效果比较平坦、缺乏立体感。这时候通常采取近似可见性的技术进行弥补，且通常在屏幕空间实现，以增加画面的立体感，例如基于屏幕空间的环境遮挡[1]（Screen Space Ambient Occlusion，SSAO）等算法。

然而，在某些情况下，渲染技术需要使用更加精准的可见性判断。基于光照探针的全局光照算法[2]是一种基于预计算的全局光照算法[3]，常被应用于电子游戏、虚拟现实等对实时性要求较高的领域和计算性能较低的移动端中。在基于光照探针的全局光照算法中，光照探针稀疏地分布在场景中，光照探针呈球状，每个光照探针捕捉了球面各个方向的光照信息。渲染时，每个着色点的光照信息由其周围的几个光照探针提供（本文称为局部光照信息）。如环境遮蔽等近似可见性的算法由于缺乏方向性信息，对渲染画面的立体感提升不强，此时，物体的三维表面上需要更加精准的可见性。而精准的可见性需要在每个着色点的法线半球的各个方向上进行判断，具有较大的计算量，难以实时计算。

本文基于预计算的思想，利用球谐函数[4]作为球面基函数离线预计算三维模型表面的可见性分布；为了进一步压缩存储量，构造误差函数，利用最小二乘拟合将球谐函数表达的可见性分布进一步压缩为可见性圆锥；实现了一种高精度、低存储量的可见性算法。

1 算法实现

1.1 基本思想

给定三维模型表面上的一个点x，其可见性是一个定义在点x的法线半球上的方向分布函数。球谐函数是定义在单位球面的标准正交的基函数，它忽略半径大小，仅考虑球面的方向变化，常用于表达球面上的方向分布函数。因此，本文采用球谐函数拟合可见性分布，将其投影到球谐函数的n个基函数的线性组合，并存储为n个基函数的系数（权重）；接着，为了进一步压缩存储量，本文采用可见性圆锥作为最终存储可见性的数据结构，可见性圆锥包含主可见方向、可见角度、可见性放缩因子，对可见性分布具有灵活地表达。压缩方式是：通过构造误差函数，利用最小二乘拟合[5]求解（局部）最优解，将球谐函数表达的可见性分布压缩为一个可见性圆锥。

1.2 算法细节

本节主要描述算法的具体细节。首先对球谐函数进行概述；接着，描述如何将一个点在其法线半球上的可见性分布投影为球谐函数；然后，描述如何构建误差函数，将球谐函数表达的可见性分布压缩为可见性圆锥；最后，简单介绍本文在判断可见时使用的遮挡距离加权方式。

（1）球谐函数

球谐函数的定义如公式（1）所示，其中，l表示当前基函数的带（band，也称为阶数，下文统一用阶数表示），m表示在第l阶中第m个基函数（m∈[-l,l]），表示相应的勒让德多项式表示规则化的缩放系数，其计算方式如公式（2）所示。参数l将球谐函数分成不同阶，每个阶数内包含2l+1个基函数，它们具备相同的多项式次数。前n阶包括n2个基函数，对原始函数的n阶近似则需要存储n2个系数。

将一个球面函数投影为球谐函数系数的过程称为投影，计算系数即对原函数和球谐函数的基函数进行积分，如公式（3）；反之，将球谐函数按对应的系数进行线性组合，重建对原函数的近似称为重建，如公式（4）。

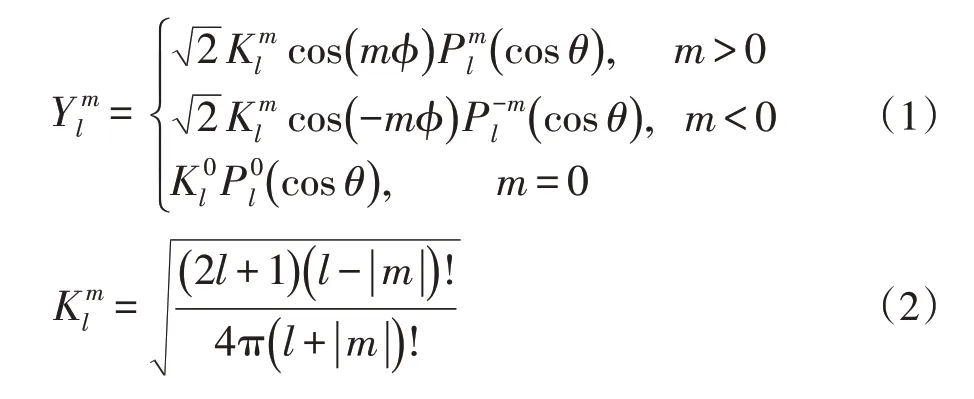
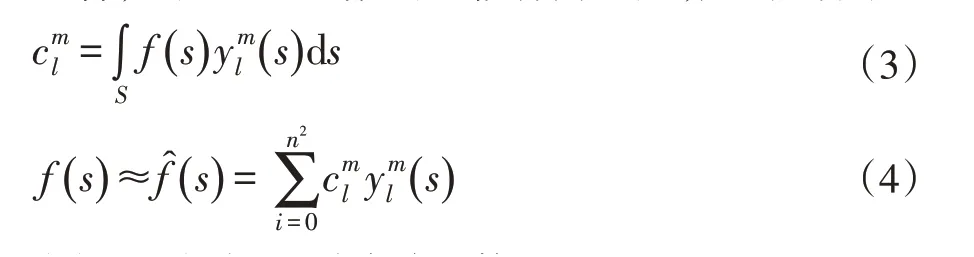
（2）可见性投影到球谐函数

本文采用4阶球谐函数（16个基函数）来近似可见性分布。其基本思路是：对于三维模型表面上任意一个点x，首先在其法线半球上均匀采样，并判断各个方向可见或是被遮挡，接着将每个采样方向投影到球谐函数上，累计该采样方向对系数的贡献，最终得到16个系数。由于本文是离线计算，故直接采用遍历的方式来得到球面上呈均匀分布的各个方向，以确保球面各个方向都有采样值，而没有采取均匀分布生成随机数的计算方式。采用球面均匀采样的原因是：每个采样方向的权重都相同，计算其对最终系数的贡献十分简单准确。

（3）可见性圆锥

可见性圆锥由主要可见方向、可见角度和可见性放缩因子构成。主要可见方向的定义类似Bent Nor⁃mal；可见角度定义了主要可见范围；可见性放缩因子为可见性圆锥的大小，其范围在0～1之间，当一个点被多个方向遮挡时，可以将可见性放缩因子设置得小一点，更加灵活地表达可见性分布。将可见性分布压缩为可见性圆锥的过程就是求解可见性圆锥的三个元素，主要可见方向可以直接由球谐函数的optimal linear方向得到，剩余的就是求解可见角度α和可见性放缩因子S。利用最小二乘拟合的推导过程如下：

首先将可见性圆锥用球谐函数的表示方式（公式（5）），并构造误差函数（公式（6））。

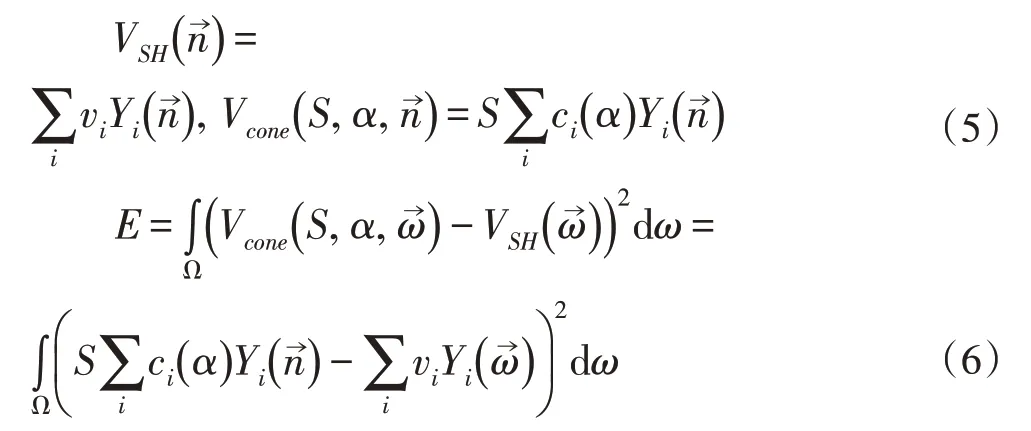
接着，误差函数分别对α和S求导，并将导数置为0，求解可得到最优解（公式（7））。但这一步的难度在于这个导数定义在半球面，难以直接求解。

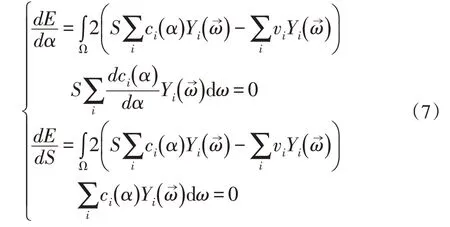
借助球谐函数的标准正交性，有式（8）成立，即两个球谐函数的积分可以转化为其系数的点乘。从而可以对式（7）中进行化简，得到式（9）。

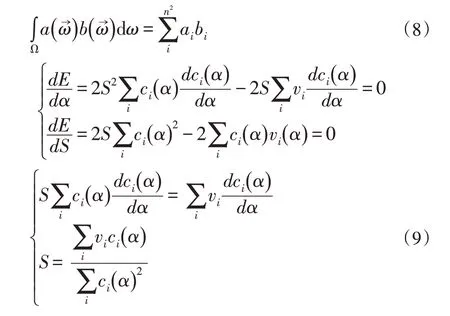
最后，对式（9）利用最小二乘拟合即可求解出α和S的最优解，最终就将由16个浮点数表示的可见性分布函数压缩成了可见性圆锥。可见性圆锥包含5个浮点数，将主要可见方向保存在切线空间后可以进一步压缩成4个浮点数进行存储。

（4）遮挡距离加权

前文提及，某个方向的可见性判断是一个布尔值，即可见或被遮挡。然而，由于球面上的方向分布本质是一个连续函数，而在球面上进行采样的思路是对其离散化进行近似，只有当采样次数达到极高时才能完全拟合球面的分布函数。但在实际应用中，我们在球面的采样次数有限，一个立体角内仅有一个采样方向。为了对这一矛盾进行弥补，本文采用对遮挡距离进行加权。即：对于一个立体角来说，该采样方向遮挡距离远，那么该立体角内所有方向被遮挡的概率就更低；反之，若遮挡距离近，则表明该立体角内所有方向被遮挡的概率更高。本文采用公式（10）的方式计算权重，其中docc是指被遮挡的距离，dmax是指模型的对角线长度。

2 实验结果

实验一：验证可见性圆锥的正确性。

通过在可视化模型上可见性圆锥的三个元素，验证可见性圆锥的正确性。可见性圆锥可视化预期结果是：主可见方向在模型未遮挡的地方与法线一致、存在遮挡的地方会在两个面片之间平滑过渡；可见角度在未被大面积遮挡的地方角度更大，可视化结果接近白色、相互遮挡之处较小，可视化结果接近黑色；而在非常狭窄的地方，可见性缩放因子较小，可见角度较大。

在模型上可视化可见性圆锥的结果如图1所示，符合上述预期特点，因此可见性圆锥计算基本正确。实验二：验证遮挡距离加权的正确性。

图1 可见性圆锥

本实验的目的是验证遮挡距离加权的正确性，预期目标是遮挡距离加权后三维模型表面上的可见性的分布更加准确和平滑。本实验选择表面更加复杂的汽车模型，实验结果如图2所示，可以发现，对遮挡距离进行加权后，可以得到更加平滑、自然的可见性分布。

3 结语

本文提出基于预计算的思想，以球谐函数作为球面基函数表达三维模型表面的可见性分布，并进一步将其压缩为可见性圆锥，得到了一种高精度、低存储量的预计算可见性。该算法可用于解决其他光照算法中可见性缺失所造成的光照结果平坦、缺乏立体感的问题，具有一定的实际意义。

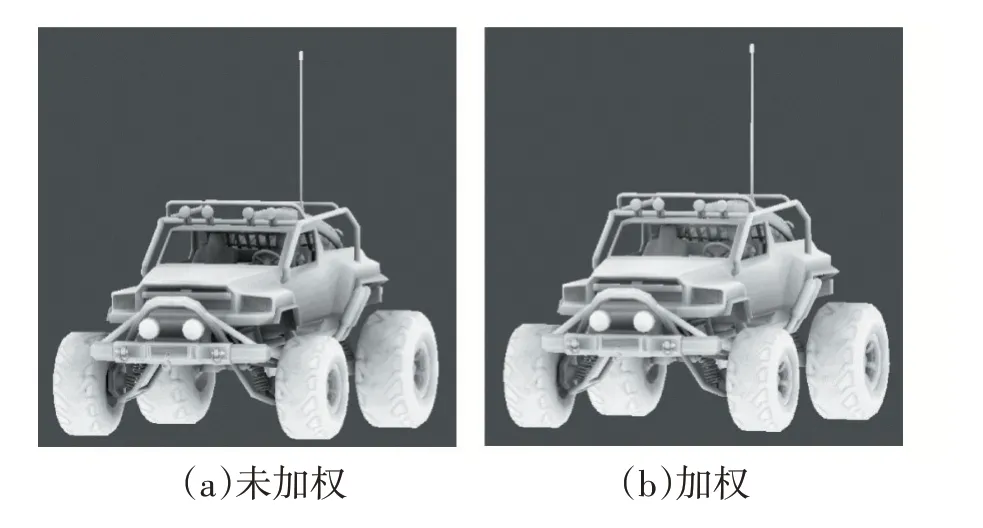
图2 遮挡距离加权对比实验