基于聚光太阳能的油品管道减阻与节能研究*
2020-03-31
常州大学石油工程学院
近年来,我国的工业化进程持续快速发展,石油在我国经济发展中占据重要地位。代晓东等[1]研究分析了BP公司每年发布的世界能源统计年鉴和能源展望,预计到2040年石油、天然气、煤炭和非化石能源将各占世界能源的四分之一,其中石油稳定发展。我国的石油运输有管道运输、水路运输、铁路运输和公路运输等输送方式,管道运输因其具有安全性好、效率高、运输量大、成本低等优点成为石油运输的主要方式。石油管道运输是最适宜于输送石油的一种运输方式,是连接上游石油资源与下游石油商品的有效途径,是石油运输业重要的一部分[2]。孙玉龙[3]提出长输管道是我国能源消耗较大的行业,在输送石油时需要有效地降低输送过程中的摩擦阻力以及散热损耗。迄今为止很多学者对如何降低石油在管道运输中的阻力进行了研究。杜勇等[4]和胡景磊[5]使用DRIVE原油萃取剂进行的实验发现,DRIVE原油萃取剂具有良好的原油清洗力,可改善原油品质,减小原油在集输过程中的流动阻力。同时也有很多人对管道减阻剂进行了研究,马永义[6]对EP系列减阻剂的应用进行了相应的探究。车福利等[7]通过实验研究了聚丙烯酰胺(PAM)溶液减阻剂的减阻性能。李恩田等[8]自行设计了管道流动试验平台和PIV测试系统,并与平板表面对比发现肋条具有减阻效果,并且减阻率与归一化肋高h+、雷诺数Re有关。崔迪等[9]和谭德金[10]对降凝剂、降凝技术革新进行了一定的探讨,对相关技术的发展情况进行了分析。JING和QI等[11]研究了表面润湿性对湍流水平流动摩擦阻力的影响,并且对5种不同的管材进行了研究,通过实验证明,表面润湿性对宏观管道中流体的摩擦因数有一定影响。齐红媛等[12]还用实验证明了对于相同的管输液体,可通过更换管输的材质改变润湿性,进而降低流动阻力。
为了响应国家“十三五”规划中加大可再生能源的利用政策,提出了利用聚光太阳能加热油品的减阻系统。利用ANSYS有限元分析方法对油品管道进行数值模拟,并将模拟结果与理论分析结果进行对比分析,研究了管长和聚光比对管道出口温度的影响,并对减阻效果进行了相应的分析。
1 系统原理
太阳能聚光输油管道系统结构如图1所示。该系统在输油管道的下方设有CPC折线形聚光器,其聚光倍数可达到2~6倍,太阳光可通过CPC聚光器上的抛物面反射聚集到石油管道表面,从而达到加热输油管道内油品的目的,并且在管道的末端连接一个高效的油水板式换热器,该换热器可用来收集管道内的油品在整个管道输送过程中所获得的热量,实现能源的高效利用。
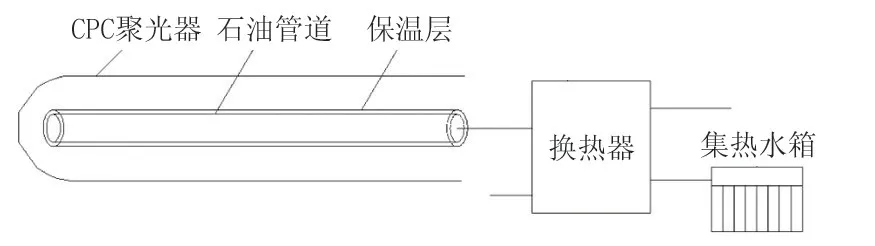
图1 太阳能聚光输油管道系统结构Fig.1 Structure of concentrating solar energy oil pipeline system
数值模拟主要用于计算石油经较长的管道输送后最终石油的温升,以及得到该温升所节约的能量,因此模拟只对输油管道进行模拟,忽略管道末端原有的高效油水换热器。同时为了简化模型并且不影响整个计算结果,在建模过程中忽略了CPC聚光器的存在,但在后续的FLUENT计算中,在太阳辐射模型里太阳射线追踪法中的太阳直射辐照度改为经过CPC聚光后达到的光照强度,这样可以简化模型并且不会影响计算结果。如图2所示,太阳光经CPC聚光器聚光后的总能量主要由管道中的油品吸收,损失的能量主要为升温后的管道与环境之间的辐射换热与对流换热,同时由于CPC聚光器的结构对管道有保护作用,对流换热损失的能量非常小,可忽略不计。

图2 管道能量流示意图Fig.2 Schematic diagram of pipeline energy flow
2 理论分析
设太阳的单位面积辐照强度为G,聚光输油管道接收辐照的面积为A1,其吸收率为α,CPC聚光光伏的聚光倍数为n,则输油管道接收的总能量Q为

式中:n为CPC聚光光伏的聚光倍数,取值范围为2~6;d为输油管路的直径,m;l为输油管路的长度,m。
输油管路接收的总能量Q一部分为石油加热所需的能量,一部分将以辐射的形式散失到环境中,即

式中:h1为输油管壁与石油的换热系数,W/(m2·K);A2为输油管壁与石油的接触面积,m2;Twall为输油管壁的温度,K;Toil为石油的定性温度,K。
输油管壁与石油的换热系数h1的计算式为


式中:Nu为努赛尔数;Re为雷诺数;Pr为普朗特数;de为当量直径,m;λ为石油的导热系数,W/(m·K);ρ为石油的密度,kg/m3;u为石油的流速,m/s;μ为石油的动力黏度,Pa·s。
输油管壁与石油的接触面积A2的计算式为

式中:d为输油管路的直径,m;l为输油管路的长度,m。
石油的定性温度Toil的计算式为

式中:Tout为石油的出口温度,K;Tin为石油的进口温度,K。
以辐射的形式散失的能量Qloss的计算式为
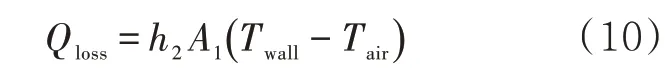
式中:h2为输油管壁与环境的换热系数,W/(m2·K);Tair为环境温度,K。
输油管壁与环境的换热系数h2的计算式为

式中:σ 为斯蒂芬波尔兹曼常数,5.67×10-8W/(m2·K4)。
加热石油所需的能量Qhot即为石油得到的热量Qoil,对其计算采用如下公式

式中:Cp为石油的比热容,J/(kg·K);qm为石油的质量流量,kg/s;A3为输油管路的横截面积,m2。
3 数值模拟
计算流体力学(CFD)是通过计算机进行数值计算,模拟流体流动时的各种相关物理现象,包括流动、热传导等。目前,计算流体动力学是解决流动和传热相关问题的强有力工具。本文基于流体为不可压缩、稳态紊流假设,运用ANSYS Fluent软件,采用标准k-ε湍流数学模型模拟石油在该输油管路中的温度场和速度场的分布规律,采用CFD主要解决了前处理、求解和后处理问题。
3.1 三维模型的建立
利用ANSYS软件中的前处理软件ICEM CFD,根据该输油管道的几何和物理特性,经过点、线、面的绘制得到该管道简化的三维模型,并创建好相关部分,同时对该模型进行网格划分,网格类型根据石油管道的物理特性选择O型网格划分,结果如图3所示。

图3 有限元网格图Fig.3 Finite element grid chart
3.2 控制方程与条件加载
在三维稳态条件下建立了该模型,利用CFD方法对油品运输管道的性能进行了数学模拟。将整个输油管道考虑为控制体,连续性、动量和能量的控制方程为
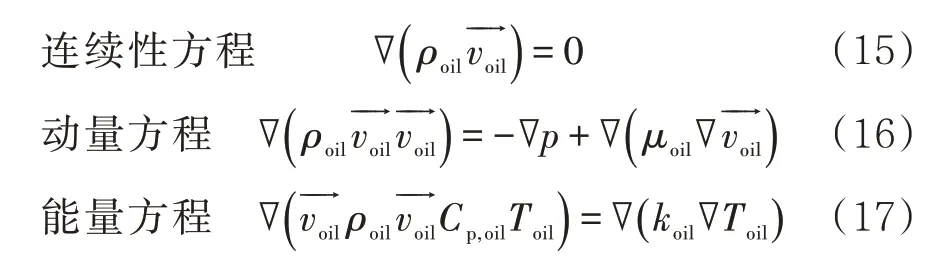
式中:v→为管道内油品的速度;p为压力。
将入口设置为“速度入口”边界条件,该边界条件包含了冷却流体的入口速度和温度,其中油品的初始速度为1 m/s,初始温度为20 ℃,外界环境温度设为20 ℃,同时油品管道的出口选用“压力出口”边界条件。将太阳辐射模型中的射线追踪法里的直射辐射强度设为3 000 W/m2,同时在材料属性的设置中将输油管道的薄壁厚度设置为8 mm。本文利用基于压力的有限体积法(FVM)对控制方程进行离散化求解;采用简单的算法进行压力-速度耦合;采用二阶迎风法求解动量方程和能量方程;利用连续方程、动量方程和能量方程的残差值作为收敛的标准。连续性方程、动量方程和能量方程的最大残差分别小于10-5、10-6和10-8,经过一定的迭代求解可得到相应的模拟结果。
3.3 模拟结果
3.3.1 温度场模拟结果
当石油管道管长为1 000 m,管内径为0.5 m,壁厚为8 mm,石油入口温度为20 ℃,入口速度为1 m/s,环境温度为20 ℃,太阳辐射强度为600 W/m2,CPC聚光器聚光倍数为5,管道的温度分布如图4所示。

图4 出口截面温度分布Fig.4 Outlet section temperature distribution
从图4可以看出,石油管道出口截面的温度分布基本均匀,管壁温度稍高于管内石油温度,从管壁到管道中心呈降低趋势,这是由于流体热传导的特性所产生的。
3.3.2 速度场模拟结果
在上述相同条件下,可以得到石油管道出口流体速度分布云图(图5)。
图5清晰地显示出在近壁面处流体流动速度很小,并且在径向方向逐渐增大,最后形成如图5所示的同心圆形状。这是由于紊流中横向脉动所引起的流层之间的动量交换,使得管流中心部分的速度分布比较均匀;而在靠近固体壁面的地方,由于脉动运动受到壁面的限制,黏性的阻滞作用使流速急剧下降[13],形成如图5所示的同心圆状。
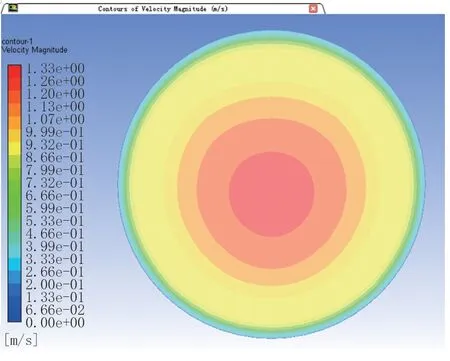
图5 管道出口速度分布Fig.5 Pipeline exit velocity distribution
图6为石油管道入口x=0截面的速度矢量图。从图6可以看出流体在入口处的速度分布较均匀,这是由于在入口处有输入动力的存在使得流体在入口处附近以一个均匀的速度场进入石油管道,随着流体在管道内的深入,入口输出动力的影响会大大减弱,流体的速度场会逐步形成与图5一样的同心圆状。
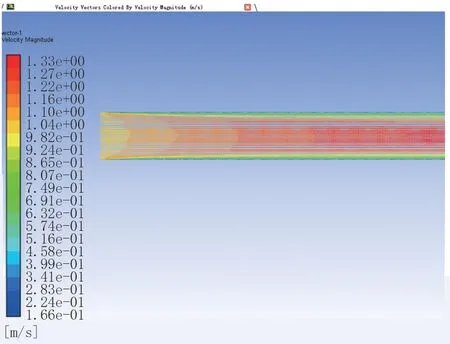
图6 x=0截面入口速度矢量图Fig.6 Section entrance speed vector when x=0
4 对比分析
图7反映了聚光比为5、环境温度为20 ℃、石油入口温度为20 ℃、流速为1 m/s时流体的温升随管长的变化趋势。从图7可以看出随着管长的增加,温升逐渐扩大,也就是出口温度在逐渐增加,当管长增加到8 km时,温升达到了40 ℃,也就是此时石油的温度为60 ℃,因此在实际工程应用当中,可以在长输管道的末端得到很高的出口温度,末端的换热器将会换取并存储大量的热量。另外,理论计算的温度和Fluent模拟出来的温度误差范围不大,并且随着管长的增加误差有些许的加大并且趋于不变,出现误差些许增大是由于理论计算是在理想状态下进行的,而模拟更偏向实际情况,但是随着管长的增加误差会趋于定值。
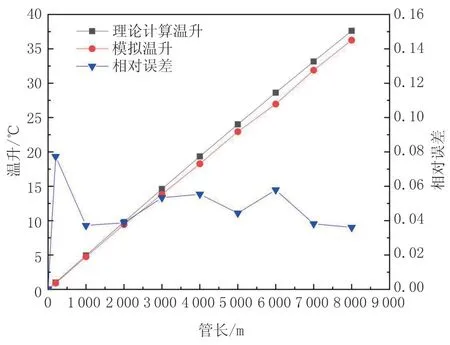
图7 理论温升和模拟温升随管长变化关系Fig.7 Theoretical temperature rise and simulated temperature rise as a function of tube length
图8反映了环境温度为20 ℃、石油入口温度为20 ℃、流速为1 m/s、管长为1 000 m时流体的温升与聚光比之间的关系。从图8可以看到随着聚光比的增加,温升在逐渐扩大,即出口温度在逐渐增加,理论计算温度与模拟温度误差范围并不大。当聚光方式换成其他高倍聚光形式,聚光比会增大近百倍,因此只需要对很短的一部分输油管道进行加热就可以达到CPC聚光器长距离的聚光加热效果,可以简化管线的结构。

图8 理论温升和模拟温升随聚光比的变化Fig.8 Theoretical temperature rise and simulated temperature rise as a function of concentration ratio
从图7和图8中可以看出,输油管路中油品的模拟温升与理论计算得出的温升误差并不大。在管长为1 000 m、5倍聚光时,理论计算的温升与模拟得出的温升误差仅为3.787%,在误差允许范围内。两者之间存在的误差主要是在三维建模的过程中对模型进行了相应的简化而造成的细微的误差,以及在理论计算时对一些数据进行了四舍五入,只保留前几位数作为该数的近似值而造成的误差。
针对不同的油品[14],通过计算得出摩阻系数与温度和管长的关系,如图9、图10所示。
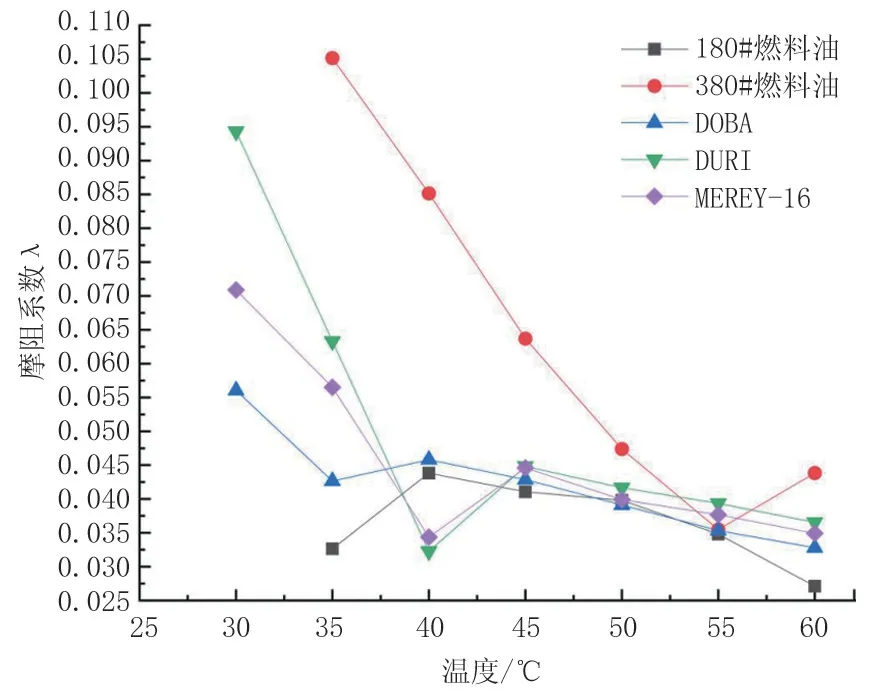
图9 摩阻系数与温度的关系Fig.9 Relationship between friction coefficient and temperature
图9显示了随着温度的升高,摩阻系数并不是一味地降低,大多数呈现先降低然后升高再降低的趋势。这是由于温度的升高导致油品的运动黏度降低,则雷诺数升高,管道内油品的流动特性会从层流变为湍流,摩阻系数会有略微的升高,然后再继续降低。图10中摩阻系数的变化趋势与图9类似,由于管长的增加,管内油品的温度持续升高,出现与图9类似的变化趋势。同时,得到了在不同聚光倍数情况下摩阻系数最小值时的管长,表1为5种油品在不同聚光比时的最佳加热管长,油品中转站可根据实际的输送距离选择合适的聚光比。
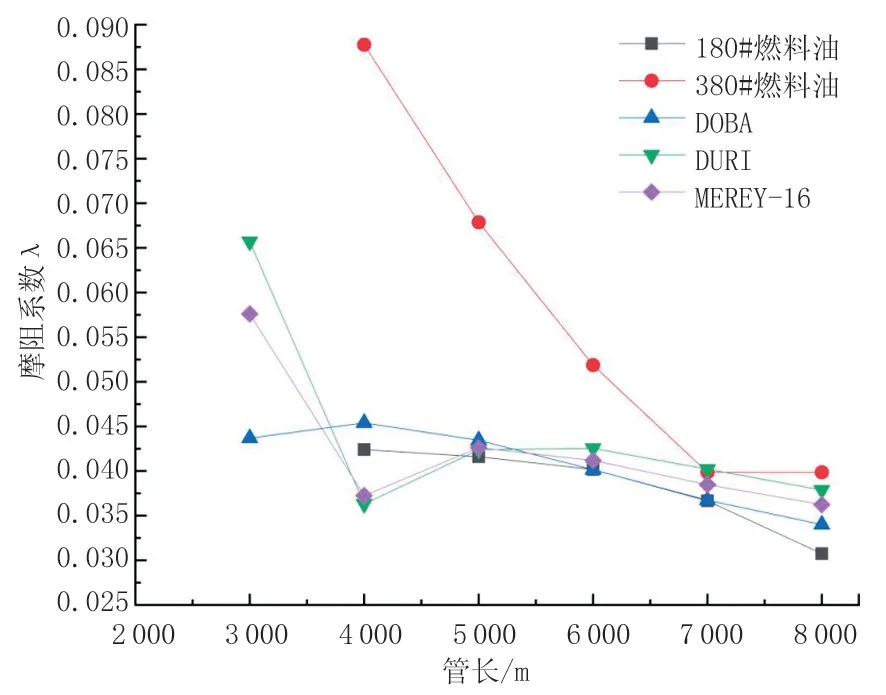
图10 摩阻系数与管长的关系Fig.10 Relationship between friction coefficient and tube length
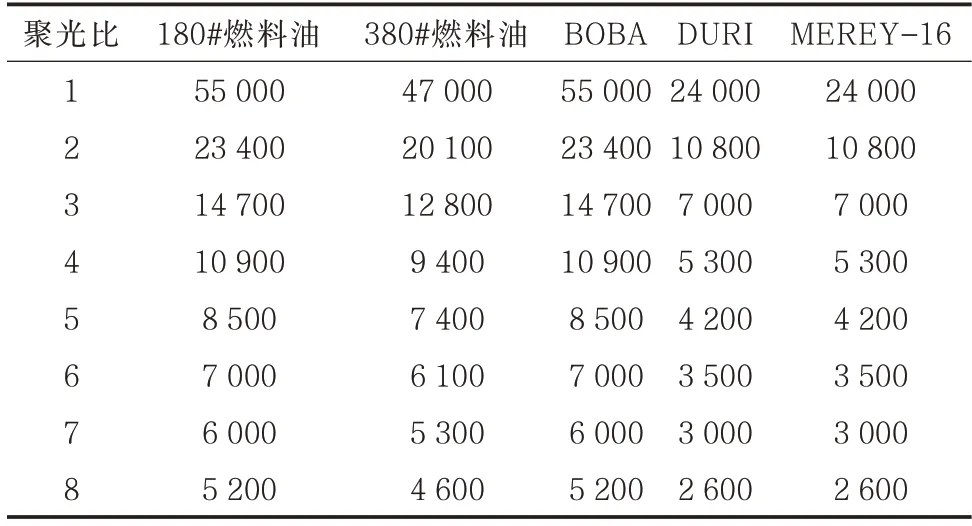
表1 不同聚光比的油品最佳加热管长Tab.1 Optimum heating tube length for oils with different concentration ratios m
5 结论
通过对石油管路太阳能聚光减阻及集热系统进行的模拟研究和理论验证,得到以下结论:
(1)输油管路的出口温度随着管长的增加而上升。在5倍聚光下,石油进口温度为20 ℃、速度为1 m/s、环境温度为20 ℃时,石油每通过200 m输油管路温度会提升约1 ℃。在实际的工程中,仅需要对输油管道的前8 km安装CPC聚光器进行加热就可以得到60 ℃的高温热油,同时在末端利用换热器进行换热,可换取可观的热量。
(2)输油管路的出口温度随着聚光器聚光比的增加而上升。当聚光比达到100时,仅需要在管道的前段部分聚光,出口温度就可以达到CPC聚光器长距离的聚光集热的温度,可以简化管线的结构。
(3)模拟得出摩阻系数与温度和管长的关系曲线,以及不同油品达到最佳减阻效果的加热管长。
