超拓扑空间上的可乘性质
2020-03-31张国芳
温 然,张国芳
(吉林师范大学 数学学院,吉林 四平 136000)
0 引言
1983年,Mashhour与A.A.Allam在《On Supra Topological Spaces》[1]中定义了超拓扑空间:2X的一个子集族μ叫做X上的超拓扑,如果满足下面两个条件:1)X∈μ.2)μ中元素的任意并仍在μ中.偶对(X,μ)称为超拓扑空间,μ中元素称为超开集,超开集的补集为超闭集并研究了这些概念的一些关系.介绍了超拓扑空间中S连续映射和S*连续映射定义,并给出S连续映射和S*连续映射的等价条件.给出了S-T0空间、S-T1空间及S-T2空间,称超拓扑空间X为S-T0空间,如果对于X中不同两点,存在其中一点的超邻域不包含另一点.称超拓扑空间X为S-T1空间,对于X中不同两点x,y,存在两个超开集使得x∈U,y∉U且x∉V,y∈V.称超拓扑空间X为S-T2空间,对于X中不同两点x,y,分别存在x,y的两个超开集U与V,使得U∩V=Ø.
2008年,T.H.Jassim在《On Supra Compactness in Supratopologicol Spaces》[2]中研究了超拓扑空间中超紧空间的性质,得出超紧空间的任何超闭子集是超紧的、任何有限超拓扑空间是超紧的、超紧空间在S*连续映射下的像是超紧的等结论,还定义了超拓扑的笛卡尔积,并证明了两个超紧空间的笛卡尔积是超紧的.
2016年,T.M.AL-shami 在《Some Results Related to Supratopological Space》[3]中给出超闭包算子、超lindelö空间、超正规、超正则及STi-空间的定义,称超拓扑空间X为超正规的,如果对于X中每个超闭集F和每个a∉F,存在超开集G和H,F⊂G,a∈H,有G∩H=Ø.称超拓扑空间X为超正则的,对于X中每个不相交的超闭集F1,F2,存在两个超开集G和H,分别包含F1,F2,有G∩H=Ø.称超拓扑空间X为ST3-空间:如果X既是ST1-空间又是超正规空间.称超拓扑空间X为ST4-空间:如果X既是ST1-空间又是超正则空间.并举例说明超正规空间不具有超遗传性.
1 预备知识
定义1[4]设X是一非空集合,X的一个子集族μ称为X的一个拓扑,如果它满足:
1)X,Ø都包含在μ中.
2)μ中任意多个成员的并仍在μ中.
3)μ中有限多个成员的交集仍在μ中.则偶对(X,μ)称为拓扑空间,μ中元素称为开集.
定义2[5]集族B⊂O叫做拓扑空间(X,O)的基,如果X中每个非空开集都可由B的某个子集族的并表示.
定义3设是超拓扑空间X的超拓扑,⊂如果中每一元素是的某个子集族的并,称是超拓扑空间X的超基.
定义4设X1,X2是两个集合,记X1×X2为它们的笛卡尔积,以{U1×U2|U1∈1,U2∈2}为超基的超拓扑,叫做X×Y上的超积拓扑,则称(X1×X2,)为超积拓扑空间.
定义5[6]设(X,ι)是超拓扑空间,取x∈X,U是X的子集,若存在超开集V∈ι,使得x∈V⊂U,则称U是点x的超邻域.
定义6某超拓扑空间的一个超基或在某一点处的一个超邻域基,如果是一个可数族,则分别简称为一个可数超基和一个可数超邻域基.
定义7一个超拓扑空间如果有一个可数的超拓扑基,则称此超拓扑空间满足第二超可数性公理.
定义8一个超拓扑空间如果在它的每一点处有一个可数超邻域基,则称此超拓扑空间满足第一超可数性公理.
定义9设X是一个超拓扑空间,A⊂X,如果D的超闭包等于X,即scl(A)=X,则称D为X的一个超稠密子集.
定义10设X是一个超拓扑空间,如果X中有一个可数的超稠密子集,则称X为一个超可分空间.
定义11一个超拓扑空间X是一个超局部紧空间,如果对所有x∈X,存在x的一个超邻域U,使得scl(U)是X的一个超紧子空间.
2 主要结果




定理1若X1,X2是满足第二超可数性公理的超拓扑空间,则超积空间X1×X2满足第二超可数性公理.

定理2若X1,X2是满足第一超可数性公理的超拓扑空间,则超积空间X1×X2满足第一超可数性公理.

所以∪B(x)×B(x′)为X1×X2的超邻域基,又∪B(x)×B(x′)是可数的,所以∀x∈X1,∀x′∈X2,∪B(x)×B(x′)是X1×X2的可数的超邻域基,故超积空间X1×X2满足第一超可数性公理.
若E是超拓扑空间(X,τ)的子集,则包含E的所有超闭集的交称为E的超闭包,记为scl(E).下面的命题给出了超闭包的等价条件.
命题1x∈scl(A)⟺x的任一超邻域U,都有U∩A≠Ø.
证明 必要性:1)x∈scl(A)=A∪As′,x∈A,则x的任意超邻域U,有U∩A⊃{x}≠Ø.
2)x∈As′,则x的任意超邻域U,有U∩(A{x})≠Ø,即U∩A≠Ø.
充分性:1)x∈A⊂scl(A)⟹x∈scl(A).
2)x∉A,A=A{x},x∈As'⊂scl(A)⟹x∈scl(A),故x得任意邻域U,有U∩A{x}≠Ø.
引理2若X1,X2是超拓扑空间,X1×X2是它们的乘积空间,证明对于任何A⊂X,B⊂X,有scl(A×B)=scl(A)×scl(B).
证明 设x=(x1,x2)∈scl(A×B),对于任意的超开邻域x1∈U,x2∈V,由命题1
(U×V)∩(A×B)≠Ø又因为(U×V)∩(A×B)=(U∩A)×(V∩B),所以U∩A≠Ø,V∩B≠Ø.所以x1∈scl(A),x2∈scl(B),x=(x1,x2)∈scl(A)×scl(B).
故scl(A×B)⊂scl(A)×scl(B).
反之,设x=(x1,x2)∈scl(A)×scl(B),则x1∈scl(A),x2∈scl(B).对x的任意的超开邻域W,分别存在x1,x2的超邻域U,V,且W=U×V.由于U∩A≠Ø,V∩B≠Ø.则(U∩A)×(V∩B)=W∩(A×B)≠φ.所以x∈scl(A×B),scl(A×B)⊃scl(A)×scl(B)
综上所述,scl(A×B)=scl(A)×scl(B).
定理3若X1,X2是超可分空间,则乘积空间X1×X2也是一个超可分空间.
证明 若X1和X2是超可分空间,D1,D2分别为X1,X2的可数超稠密子集,则D1×D2为X1×X2的可数子集.且scl(D1)=X1,scl(D2)=X2,由引理2,
scl(D1×D2)=scl(D1)×scl(D2)=X1×X2.
所以D1×D2为X1×X2的可数超稠密子集,即X1×X2是超可分空间.
引理3[2]若X,Y都是超紧空间,则乘积空间X×Y也是超紧的.
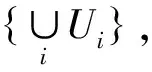
定理4若X1,X2都是超局部紧空间,则乘积空间X1×X2也是超局部紧空间.
证明 设X1,X2是超局部紧空间,x=(x1,x2)∈X1×X2,则分别存在x1,x2在X1,X2中的超邻域U1,U2,使得scl(U1),scl(U2)分别为X1,X2的超紧子空间.且有U1×U2为x的超邻域,由引理3,超紧空间与超紧空间的笛卡尔积是超紧的,从而scl(U1)×scl(U2)=scl(U1×U2)为X1×X2中的超紧子空间,所以X1×X2为超局部紧空间.
定理5若X1,X2都是S-T0空间,则超积空间X1×X2也是S-T0空间.
证明 若X1和X2是S-T0空间,(x1,y1),(x2,y2)是X1×X2中互异的两点,则有x1≠x2,y1≠y2.因为X1为S-T0空间,所以在X1中有超开集U仅含x1与x2之一,不妨设x1∈U,x2∉U,则P-1(U)是X1×X2中点(x1,y1)的超开邻域,且其不包含(x2,y2),故X1×X2为S-T0空间.
定理6若X1,X2都是S-T1空间,则乘积空间X1×X2也是S-T1空间.
证明 若X1和X2是S-T1空间,设x1,x2为X1中互异两点,y1,y2为X2中互异两点,则(x1,y1),(x2,y2)是X1×X2中互异的两点.因为X1为S-T1空间,在X1中有超开集U,V使得x1∈U,x2∉U且x2∈V,x1∉V,则P-1(U)是X1×X2中,点(x1,y1)的超开邻域且(x2,y2)∉P-1(U).P-1(V)是X1×X2中点(x2,y2)的超开邻域,且(x1,y1)∉P-1(V),则X1×X2也是S-T1空间.
定理7若X1,X2都是S-T2空间,则乘积空间X1×X2也是S-T2空间.
证明:设X1,X2都是S-T2空间,(x1,y1),(x2,y2)是X1×X2中互异的两点,则x1≠x2或y1≠y2,不妨设x1≠x2,则X1中有x1与x2的不相交的超开集U与V.U×X2与V×X2就是(x1,y1)与(x2,y2)的不相交的超开集.则X1×X2也是S-T2空间.
引理4[3]假设(X,μ)是超拓扑空间,则下面条件是等价的
1)(X,μ)是超正则的.
2)对每个a∈X和a∈U∈μ,则存在V∈μ,使得a∈V⊆scl(V)⊆U.
定理8若X1,X2都是S-T3空间,则乘积空间X1×X2也是S-T3空间.
证明 由引理4,设(x,y)∈X×Y且W为(x,y)的一个超开邻域,则存在x与y的超开集U1与U2,使得U1×U2⊂W,由于X1,X2都是S-T3空间,则存在x与y的超开集V1与V2,使得scl(Vi)⊂Ui(i=1,2),于是V1×V2是(x,y)的超开集,并且scl(V1×V2)=scl(V1)×scl(V2)⊂U1×U2⊂W.则X1×X2也是S-T3空间.
3 结束语
将拓扑空间上的有限笛卡尔积延伸到超拓扑空间上,根据超拓扑空间上已有的基础知识定义了超可数公理、超可分性质及超局部紧性等概念,并研究了这些性质在超拓扑空间都有可乘性.
