广义系统输出导数比例反馈的脉冲控制

翟昌海

(吉林师范大学 数学学院,吉林 长春 130000)

0 引言

广义系统是比正常系统更具普遍形式的动力系统[1],广义系统理论的发展是从20世纪70年代开始的,并逐渐发展起来成为现代控制理论的一个独立分支[2].近年来,很多系统与控制领域的专家做了很多研究,同时也取得了很多卓越的成就.在控制理论中,无论是古典控制理论[3],还是现代控制理论[3],反馈控制都是设计系统的主要方式.它体现了系统能控的实用价值,能够更好地改善系统.反馈控制可分为状态反馈和输出反馈两个基本类型[4,5].

然而,在大多数的文献中,学者都是针对比例状态反馈或比例输出反馈构成闭环系统的脉冲控制问题进行研究,对于输出导数比例反馈[6]构成的闭环系统的研究并不多见.然而,在一定条件下,同样可以使得输出导数比例反馈[7]构成的闭环系统无脉冲.本文主要研究导数比例反馈构成的闭环系统无脉冲的充要条件.

1 主要引理

引理1[8]设广义系统

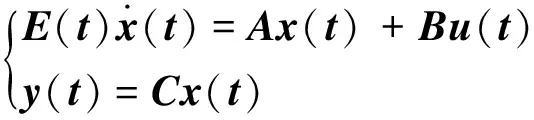
(1)

能检测且脉冲能观,且E0∈Rn×(n-q)列满秩且满足ETE0=0,则下列命题等价:

1)广义系统(1)是容许的.

2)存在矩阵X≥0和M∈R(n-q)×n满足广义李雅普诺夫方程

(2)

3)存在矩阵X∈Rn×n和M∈R(n-q)×n满足广义李雅普诺夫方程(2)及约束

ETXE≥0

(3)

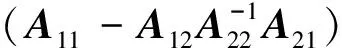
设

则方程(2)变为

TTATSST(XE+E0M)T+TT(XE+E0M)TSSTAT+TTCTCT=0

等价于

即为

(4)

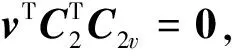
再由式(4)有

其中

(6)

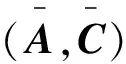
(7)

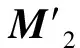
2)⟹3)是显然的.

证毕.

引理2[8]考虑广义系统

(8)

其中,x(t)∈Rn为状态，E,A∈Rn×n为定常矩阵,E为奇异矩阵,满足rank(E)=q

1)广义系统(8)是容许的.

2)存在矩阵X>0和M∈R(n-q)×n满足广义李雅普诺夫不等式

(9)

3)存在矩阵Y∈Rn×n满足下列不等式

证明 2)⟹1) 令

L=-AT(XE+E0M)-(XE+E0M)TA

由式(9)得L>0.于是有

由引理1得命题(1)成立.

1)⟹2) 因为广义系统(8)是容许的,则对任意非奇异矩阵C∈Rn×n,(E,A,C)都是能观且脉冲能观的.于是由引理1知,存在矩阵X>0和M∈R(n-q)×n满足

AT(XE+E0M)+(XE+E0M)T=-CTC<0

得命题2)成立.

命题2)与3)的等价性容易得出,由于篇幅限制本文不再加以证明.

2 主要内容

考虑如下正则的广义系统

(11)

其中,x(t)∈Rn,u(t)∈Rm和y(t)∈Rl分别为状态向量、输入向量和输出向量.E,A∈Rn×n,B∈Rn×m,C∈Rl×n,D∈Rl×n皆为定常矩阵,E为奇异矩阵.假设rank(E)=q,且degdet(sE-A)=r.

输出导数比例反馈形式如下

其中,v(t)∈Rm.广义系统(11)在其作用下构成闭环广义系统

(12)

定理1对于广义系统(11)存在输出导数比例反馈.

使闭环广义系统(12)无脉冲的充要条件是存在一个可逆矩阵X∈Rn×n和矩阵W∈Rm×n,Z∈Rm×n,满足如下线性矩阵不等式:

(13)

证明 根据引理2,闭环系统(12)是能稳且无脉冲的,当且仅当存在可逆矩阵P满足:

(14)

在方程(14)两边左乘矩阵P-T,右乘矩阵P-1,可以得到

P-T(E+BF)T=(E+BF)P-1≥0

(15)

经过整理得

[(E+BF)P-1]T=(E+BF)P-1≥0

(16)

在方程(15)两边左乘矩阵P-T,右乘矩阵P-1,可以得到

P-T(A+BK1)T+(A+BK1)P-1<0

(17)

令X=P-1,则设K1X=W,YX=Z代入(16)式和(17)式中,便得到(13)式.

证毕.

特别的,当E是非奇异时,广义系统(11)等价于

(18)

系统(18)即是正常系统;如果E退化为单位矩阵,即E=I,则广义系统(11)退化为正常系统.一般来说,广义系统的结论适用于E非奇异的情形,由此可得到以下推论.

推论1当rank(E)=n时,定理1仍然成立.

证明 当E为非奇异矩阵时,广义系统(11)成为一个正常系统,从矩阵E广泛取值的角度考虑,广义系统是对正常系统的推广,因此,定理1对rank(E)=n时的情形显然成立.

推论2当E=I时，广义系统(11)退化为如下的正常系统

(19)

闭环系统为

(20)

则闭环系统(20 )无脉冲的充要条件为:存在一个可逆矩阵X∈Rn×n和矩阵W∈Rm×n,Z∈Rm×n,满足如下线性矩阵不等式:

(21)

证明 根据引理2,闭环系统(12)是能稳且无脉冲的,当且仅当存在可逆矩阵P满足:

(22)

在方程(22)两边左乘矩阵P-T,右乘矩阵P-1,可以得到

P-T(I+BF)T=(I+BF)P-1≥0

(23)

经过整理得

[(I+BF)P-1]T=(I+BF)P-1≥0

(24)

在方程(23)两边左乘矩阵P-T,右乘矩阵P-1,可以得到

P-T(A+BK1)T+(A+BK1)P-1<0

(25)

令X=P-1,则设K1X=W,YX=Z代入(24)式和(25)式中,便得到(21)式.

证毕.

3 总结

广义系统的提出和研究到现在已有几十年的历史,经过无数学者的不断钻研已取得丰硕的成果.针对利用反馈控制消除脉冲的问题,研究者们对状态反馈使闭环系统无脉冲这一问题已得出了成熟的结论,但对于输出导数比例反馈使闭环系统无脉冲的研究还不多见.本文在现有理论的基础上,应用线性矩阵不等式的方法对这一问题进行了讨论.虽然本文对输出导数比例反馈在广义系统中的应用做了部分研究,但仍存在许多问题值得探讨.例如:考虑将输出导数比例反馈应用在时滞系统中,这也是需要进一步研究的课题.