有预期效果的SI团体知识传播模型分析
2020-03-31刘芳
刘 芳
(忻州师范学院 数学系,山西 忻州 034000)
0 引言
知识传播是指在特殊社会环境中,借助传播媒介,一部分人向另一部分人传播特定的知识信息,并期待得到传播效果的行为过程.近年来,许多学者在企业隐性知识传播与在复杂网络上讨论知识传播模式方面做了大量工作[1-3].随着计算机技术的进步与网络的发展,知识传播模式探讨呈现多样化[4],例如新媒体环境下的知识传播生态[5],淘宝村创新知识的扩散[6],等.与此同时,人们开始重视在团体、团队中的信息与知识传播[7].
团体是一种人口基数较少的群体,这个群体是由为了完成某一个目标而聚集起来的个体组成,且存在知识分享与知识传播的互动关系,经常拥有固定场所,并有明确的预期效果.团体知识传播指团体有明确的学习目的,并以语言为中心的知识传播过程.例如:短期培训、课堂教学、讨论班等.由于人口基数较少,因此可以实现快速沟通.这种知识传播的传播特征为人口基数较少,学习目的明确,有明确的预期效果.
本文将利用简单SI模型对团体的知识传播进行讨论,进行动力学分析,并讨论参数对模型的敏感性,分析其在预期效果的条件下对参数的选择,并估计参数的范围.
1 模型构建与分析
假设N表示总人口,将参与学校教育的全体分为两个仓室:没有掌握知识的人群(S),掌握知识的人群(I).从生物意义及集合的角度,明显的有N=S+I,且集合互不相交.考虑在人口规模中传播和在团体教育中传播知识的情况做如下合理假设:
1)只考虑两个仓室之间的人口迁移,这意味着没有新成员的加入,也没有旧成员的移出,总人口保持不变.
2)定义S(t)为没有掌握知识的人群,这些人能够通过自学或者与掌握知识的人接触成为掌握知识的人,并在t时刻进入I仓室.定义I(t)为掌握知识的人群.
3)各仓室成员之间的接触次数仅取决于各仓室成员的数量.学习速率β是单位时间内来自S成员的新I数,且0<β<1.
在以上合理假设的基础上,绘制了知识传播传输过程示意图(如图1所示).在图1中,箭头表示个体在仓室之间的移动.
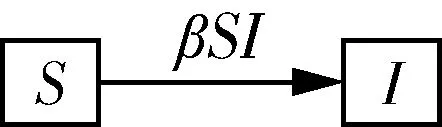
图1 知识传播传输过程示意图
基于知识传播过程示意图,建立了SI知识传播模型如下:
(1)
(2)
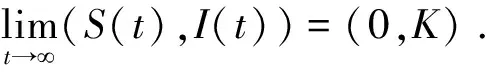
其几何意义为,在这个团体知识传播SI模型中,只要有学习效率,随着时间的增长,总是可以消灭没有知识的人群,使得在人群中完成知识传播.
2 参数对模型的敏感性分析
为了讨论参数对模型的影响,接下来将分析参数对模型的敏感性.
2.1 参数β对模型的影响
假设团体知识传播对传播效果有要求,那么提出问题:如何根据传播效果在初值条件下分析参数β.即:若已知S(0),I(0),t1时刻至多为S(t1)值,分析β的取值.
解 首先利用公式(2)中第一式,得
(3)
接下来讨论模型对参数β的敏感性分析,利用公式(2)的第一式,两边对β求导,得到
(4)
进一步由S(t)+I(t)≡K知,在t时刻,随着β的增加,S将减少,I将增加,并导致加快到达稳态的时间.
得到β的取值范围为
(5)
2.2 初值的比值对模型的影响.

解 利用公式(2)的第一式,两边对η求导,得到
(6)
由S(t)+I(t)≡K及(6)式知,在t时刻,随着η的增加,S将减少,I将增加,并加快了到达稳态的时间.
进一步提出问题:已知K,β,t1时刻S(t1)值,讨论η的取值范围.
解 利用公式(2)的第一式,解得
(7)
由(6)式,得η的取值范围为
(8)
因此,通过简单SI模型,不仅可以通过已知初值与参数分析其稳态,也可以通过初值与预期结果,给出参数的取值范围,以及分析参数与初值的比值对模型的敏感性.通过对初值与参数的分析,调整参数与初值来影响与控制知识传播,使得达到预期效果.
3 数值模拟
在一些团体知识传播中,通常会有掌握知识的人(教员)对没有知识的人(学员)进行知识传授,其教学的过程,就是以教员与学员为I与S的初始值进行知识传播的过程,教员通过各种教育形式与学员产生联系,生成学习效率.
假设K=61,S(0)=60,I(0)=1,β=0.01,利用Matlab软件绘制时间序列图(如图2所示).从图2中可以看出,随着时间的增长,(S,I)→(0,0),与理论结果相符.其几何意义为:在总人数为61的群体中,1名教员对60名学员进行某类知识传授,其学习效率为0.01,经过一段时间的学习后,所有人都掌握了知识成为掌握知识的人.验证了理论结果,只要有学习效率,随着时间的增加,总是可以掌握知识.
假设K=61,S(0)=60,I(0)=1,t1=6,S(6)=1,由公式(3)计算得β=0.022 4.利用公式(1)验算得到S(6)≈0.990 5,同时利用公式(5),可知满足条件的参数为β≥0.022 4,将计算得到参数利用Matlab进行检验,绘制时间序列图(如图3所示).验证了理论结论,在t时刻,随着学习效率β的增大,S在减少,I在增大.其几何意义为:在总人数为61的群体中,1名教员对60名学员进行某类知识传授,如果以天为时间单位,要求在第6天这个群体没有掌握知识的人仅为1人,分析学习效率的最小值.从图3中可以看出,学习效率为0.022 4时,满足预期要求.学习效率取0.027 4>0.022 4时,可以更快地达到预期,但是学习效率取0.017 4<0.022 4时,在第6天掌握知识的人没有满足预期要求.这个问题的提出,使得可以通过调整学习效率来控制知识传播.
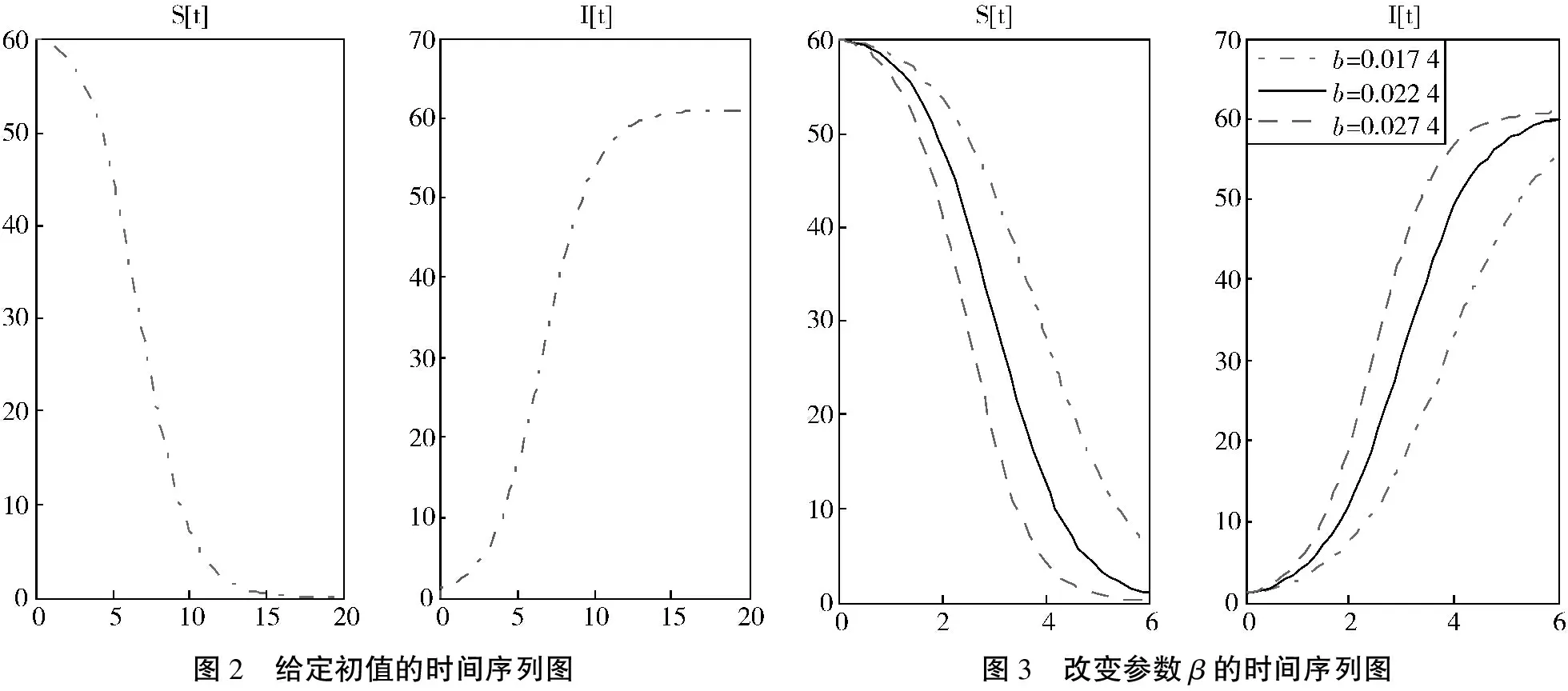
图2 给定初值的时间序列图图3 改变参数β的时间序列图

图4 改变参数η的时间序列图

4 结论
本文研究了团体知识传播模型,建立了SI动力学传播模型,给出模型的形式解.在有预期效果前提下讨论了模型对参数的敏感性,给出计算参数的公式,并得到参数的估计方法.最后利用matlab软件对知识传播进行仿真实验,验证了理论结论.
在实际操作中,团体知识传播的目的与预期效果对控制知识传播模型提出了需求.通过初值可以分析知识传播效果,也可以通过期待的传播效果来分析参数,这样通过对知识传播模型的分析可以帮助分析与控制团体的知识传播.
