基于微生物和量纲模型对茶叶货架期的研究

刘亚兵，雷志伟，李露露，潘科，沈强

（贵州省农业科学院茶叶研究所，贵州贵阳550006）

微生物生长模型（predict food microorganism growth model）是建立在微生物生长学和数学模型基础上的一门新兴学科[1]。在一定条件下，通过生长模型不仅能模拟出微生物生长的模型方程，还可用微生物模型定量的评估出食品中微生物的数量及动态变化，为延长食品货架期的寿命以及其安全性的评估提供科学的依据[2]。微生物生长模型[3]有一级模型、二级模型以及三级模型，一级模型主要反映特定条件下微生物数量与贮藏或保藏时间的变化关系；二级模型反映环境因素，如贮藏环境温度、保藏环境中所处pH 值[4-5]等对食品中所含微生物生长情况的影响；三级模型是微生物一级模型和二级模的总称，将一级和二级模型中的参数转换成网络计算机的模型，在计算机程序上可直观的呈现微生物变化情况。通过对食品中微生物预测，是管理和保障食品安全的重要工具，从微观角度探究食品质量安全及保质期的原理，为保障食品质量安全及行业发展的体系提供了合理科学依据[6]。

茶叶作为人们的日常饮用干燥食品，也是世界上最受欢迎的饮品之一[7]，富含茶多酚、儿茶素、茶红素等生物活性成分，具有许多益处，如：抗癌、增强免疫力，解渴止渴，降低胆固醇抗氧化和减肥等功效[7]，这使得茶叶越来越受到人们的青睐[8]。因此，茶叶的质量安全关系着人们的健康，解决茶叶质量安全问题关系着茶叶保质期，茶叶货架期也成为我们密切关注的话题[9]。茶叶质量安全主要是由于特定有害微生物代谢产生所导致，由于茶叶的保藏及加工环境不同，不同程度上制约着有害微生物的生长。王雪涵[10]研究表明，茶叶的加工主要是微生物发酵，通过发酵赋予茶特殊的风味和口感，在有氧条件下的发酵过程中，微生物可以将茶组织成分转化为其他活性成分，同时微生物代谢产物进入茶组织赋予了茶叶的特殊口感。另有研究表明[11]，通过厌氧发酵在亚洲许多国家受到欢迎，并给予不同的名称，如中国的川茶，缅甸的Lahpet（或Leppet-so），泰国的Miang 茶和老挝黑茶。在发酵过程中，伴随着其他腐败微生物的产生，例如霉菌，酵母菌，进而影响茶叶品质及货架期寿命。近年来，人们对茶叶中有害微生物的污染越来越重视[12]，特别是发达国家已将有害微生物限量标准作为重点检测指标。为有效防止和评估有害微生物的生长，相关学者提出多种适用于微生物生长预测模型[13-14]，模型不仅能体现微生物的数量随时间的关系，还能反映出其他因素对微生物生长数量的影响，如环境因素。常用微生物预测模型有一级模型和二级模型，包括Gompertz 方程和Logistic 方程等[15]。

近年来，国内外在开展基于食品微生物预测结合货架期预测研究已有较长的时间[16]，虽然预测模型种类比较多，但针对茶叶中有害微生物、茶叶内理化性质以及环境等因素对茶货架期预测还停留在基础阶段，研究深度不够，而且对一些微生物模型会出现使用混淆不明确现象，并不具有针对性和科学性。事实上，对于不同种类茶叶，由于贮存环境和加工条件的不同，有微生物导致品质衰败的因素有所差异，这需要根据茶叶理化特点，制定出相应的货架期评估和预测方法[17]。本文主要基于微生物生长模型对茶叶货架期的研究，建立适合评估茶叶货架期的预测模型，并借助现有的一些微生物预测模型，对其归纳、总结与建立形成茶叶货架期预测方法体系，通过量纲分析模型，从物理角度用量纲模型建立茶叶货架期的评估体系，为茶叶质量安全和健康快速发展提供科学的依据。

1 一级模型

一级模型评估在恒定的环境条件下（比如环境温度、pH 值、含氧量等）来反应微生物的生长情况[18]。微生物的生长主要由4 个部分组成，即延滞期、对数期、稳定期和衰亡期，不同时期微生物生长曲线示意图见图1。在微生物的生长过程中，由于环境因素、食品自身营养供给以及微生物本身的代谢情况，对微生物的生长产生不同程度影响。近年来，常用微生物生长一级模型有：线型模型、Logistic function、Gompertz 模型等[19]。

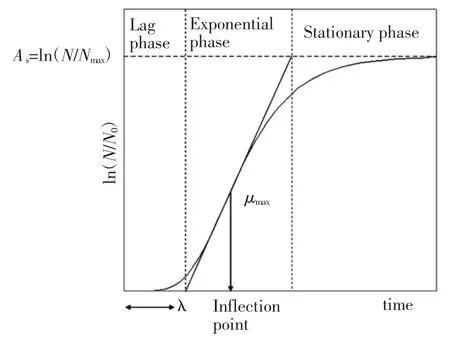
图1 不同时期微生物生长曲线示意图Fig.1 Schematic depiction of a microbial growth curve

1.1 线型和Logistic模型

微生物生长的线性模型表述为：lg Nt=M+μmt

式中：lg Nt表示微生物在时间t 时对数值；M 表示初始菌数，[lg（CFU/g）]；μm表示微生物的生长速率，h-1。

Logistic 模型表述为：

式中：log Nt/N0表示微生物在时间t 时菌落总数对数值；CA表示相对最大菌浓度，[lg（CFU/g）]，即log Nmax/N0；μm表示微生物的生长速率，h-1；tb为微生物延迟期的时间，h。

Tashiro T[20]研究表明，微生物生长一级模型直观明了，但精度不高，当有害微生物延迟期较短时，Logistic模型预测微生物并不准确。根据D.A.Ratkowsky[21]研究表明，对于一些呈酸性的食品，不适合用线型和Logistic 模型来对其进行表面微生物的生长预测，但在常温（0～37 ℃，即273 K～310 K）条件下是可行的。在复杂情况下，比如考虑环境湿度、含氧量等条件下，应考虑使用其他模型代替[22]。而罗龙新等[23]研究表明，大多数茶叶是偏酸性的食品，由于有害微生物在偏酸性条件下，延迟期较短，故不适用于一级模型进行预测。

1.2 Gompertz模型

修正后的Gompertz 方程[24]模型表述为：

式中：Nt为 t 时的微生物数量，[lg（CFU/g）]；N0为初始时微生物数量，[lg（CFU/g）]；Nmax为稳定期时微生物的最大数量，[lg（CFU/g）]；μm为微生物生长的最大比生长速率，h-1；t 为贮藏时间，h，tb微生物生长延迟期的时间，h。

在适宜微生物生长温度（16 ℃～30 ℃，即289 K～303 K）条件下，可以建立不同时间与对应微生物数量的拟合方程，从而可以确定Gompertz 方程中的各参数，确定特定温度下的微生物生长模型。Godde K[25]研究表明，Gompertz 模型适用范围较广，包括一些有害微生物，也包括茶叶在加工或贮藏中的有害微生物。

2 二级模型

微生物的来源主要是后期储藏不当，贮藏不当会导致有害微生物大量繁殖。温度和水份是影响微生物生长最关键的因素。不同微生物所适用的温度不同，例如霉菌最适合的生长温度是25 ℃，当低于10 ℃或高于30 ℃时，霉菌生长显著减弱；湿润的环境也会大大刺激霉菌的生长，渥堆的温湿度比较适宜微生物的生长。温琼英等[26]研究了黑茶渥堆过程中微生物种群的变化情况，发现传统渥堆叶比无菌渥堆叶中微生物数量多108倍以上，真菌数高300 倍～20 000 倍。为了有效的通过环境因素预测微生物的生长，常采用微生物二级模型：平方根模型和Arrhenius 方程模型。

2.1 平方根模型

平方根模型[27]主要是用来评估环境因素（如温度、水分活度、pH 值等）对微生物生长影响的预测模型，其表达式为：

式中：μm表示一级模型求出的生长速率，h-1；λ 表示模型待求的参数，℃-1h0.5；Tmin表示微生物承受的最小温度，℃；Tmax表示满足微生物承受的最大温度，℃；μmax表示最大生长速率，h-1；tb表示微生物生长延迟期的时间，h；a、b 表示常数。

Bååth E[28]研究表明，平方根预测模型使用较普遍，能够较好的对特定温度（0 ℃～37 ℃）条件下微生物的生长进行预测。Hyun J E[29]等研究表明，大多数微生物生存的适宜温度在25 ℃～35 ℃之间，但少数微生物例外，J Cepeda 等在研究沙门氏菌生长情况时，最高承受温度达到47 ℃，可知该模型的预测缺乏准确性。

An D S[30]研究表明，为算出不同温度下对微生物的影响，可根据修正Gompertz 方程和Arrhenius 方程推导的SL 公式来预测，只有确定每个温度下的μm、tb，就能计算对应温度下的剩余货架期[31]。

另外，建立食品微生物生长速率的预测模型，需要考虑多种环境因素的影响，McMeekin[32]在研究水分活度与温度对葡萄球菌生长的联合影响时发现当Tmin保持固定，对于每一个水分活度值（aw），微生物的生长速率和温度之间的关系可以用平方根模型来描述，两个变量联合修改方程为：

式中：aw(min)表示微生物生长速率为零时的水分活度；μm表示一级模型求出的生长速率，h-1；λ 表示模型待求的参数，℃-1h0.5。

Adams M R[33]等研究pH 值时和非优化温度对小肠炎耶尔森菌生长的联合作用是发现，两个变量之间是相互独立的，可用表示：

式中：pHw(min)表示生长速率为零时的 pH 值；m 表示回归系数。

Akkermans S[34]研究表明，大多数微生物生长环境的pH 值为5.0～9.0，但不同微生物的最适合生长的环境pH 值有所差异。例如，霉菌和酵母菌一般适宜在偏酸（pH 值为5 或低于5）的环境条件下生长。TA Mcmeekin 研究表明，pH 值为 5.3～7.8 时，对食品中假单胞菌没有明显的抑制作用，当pH 值为5.1～5.3 时，食品中假单胞菌生长明显减慢，pH 值小于5 则会受到抑制。罗龙新等研究表明，茶在加工和保藏时，环境pH值范围通常在5.0～8.0 之间，根据Adams M R 研究二级模型也适合对茶叶微生物的生长预测。

2.2 Arrhenius方程

在食品加工和贮藏过程中，对微生物的生长来说，温度[35]是一个很重要的主要影响因素之一。在实际分析中，假设微生物生长率受茶叶中酶促反应的影响，可在此基础上建立了Arrhenius 方程模型。Panagou E.Z[36]建立了食品温度（T/K）与食品中水分活度（aw）对微生物生长速率影响的Arrhenius 预测模型，在适宜微生物生长温度（16 ℃～30 ℃，即 289 K～303 K）条件范围外并且aw值在0.6 以下的低水分食品不适宜用Arrhenius 方程预测，因为温度过低或者过高都不适宜微生物的生长，aw值在0.6 以下时，大部分微生物已经不能存活，模型表示：

式中：μm表示微生物生长率，h-1；f0～f4表示模型参数。

D.Bermúdez-Aguirre[37]等建立了温度和丙酸浓度对寄生曲霉（Aspergillus parasiticus）生长影响的Arrhenius 模型，用Arrhenius 方程将微生物生长率表示为贮藏时间的函数关系，此方程就可以预测产毒素型真菌的生长情况。张伟等[38-39]研究表明，茶叶贮藏湿度高的条件下，大多数微生物生长适宜，且腐败微生物容易生长，故可通过Arrhenius 方程评估茶叶特定腐败微生物的生长情况。

3 量纲分析模型

量纲分析（dimensional analysis）[40]是 20 世纪初提出的一种在物理领域中建立数学模型的方法，它在试验和经验的基础上利用物理定律的量纲原则，用以确定不同物理量之间的关系。茶在实际加工和包装过程中，茶叶包装方式主要有锡制茶叶罐、陶瓷茶叶罐、纸制茶叶罐等，无论哪一种包装在贮藏过程中不仅微生物生长影响茶叶的货架期，还与贮藏环境中的物理因素有关。例如，贮藏温度k，Huang Y 等研究表明，温度越高，茶叶品质变化越快，平均每升高10 ℃，茶叶褐变速度将提高到3 倍～5 倍；贮藏时间t；茶被微生物污染的集成污垢表面积S。张小华等[41]研究表明，茶叶中主要污染微生物是枯草芽孢杆菌、阴沟肠杆菌和黑曲霉；单位体积内包装茶叶质量m；茶叶包装的总体积v；单位茶叶包装的密度p 等因素。因此，在评估茶叶货架期寿命，进行分析这些物理因素时，用量纲分析法画来分析。由此，可建立函数关系：

上述各物理量的量纲表示为：

对于上述物理量中物理量数n1=6，大于基本量纲数n1=6，即可以写出量纲矩阵：

计算R1=3，解方程：Ax=0

则方程有3 个基本解，可取：

方程式给出3 个相互独立的无量纲量：

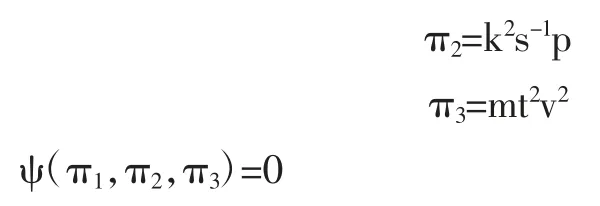
式中：ψ 表示未定函数。

在实际研究过程中，被微生物污染的污垢面积形状不一很难确求出，杨倩鹏等[42]在进行微生物污垢方面研究时发现，微生物污垢生长中期，底部细胞开始死亡，底部污垢含水量下降，体积收缩，形成中间突出的局部球体形状，定义为“突出形”，类似螺旋蜘蛛网状，假定茶叶被微生物污染后，我们把它假设成理想的标准螺旋线网状结构，则可以建立模被污染的区域呈现的相当于一个对数螺旋线的形状型求出面积。设网中心为坐标原点O，即为网的极点，顶角为α（0≤α≤设其方程为：

且（f（θ），0）的切向量为：

可得：

即为：

由此可得：

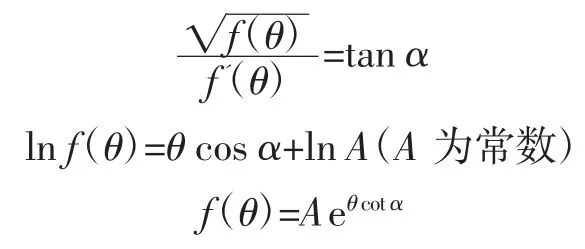
则理想等角线螺旋线的极坐标方程为：

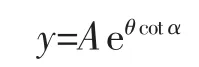
因为螺旋线（即一圈的线长）的长L1可表示为：

把β 代入下式：

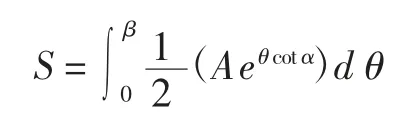
可解出S。

由量纲分析模型可知，在进行预测茶叶货架期时，通过建立ψ 函数结合物理指标预测茶叶货架期，可以正确的分析各物理量之间的关系以及对茶叶品质影响，量纲分析是预测茶叶货架期的有力工具，提供寻找物理因素对茶叶货架期影响规律的线索。

4 茶叶货架期模型建立与预测分析

4.1 微生物生长模型预测茶叶货架期

茶叶所含微生物数量情况直接关系着茶叶货架期寿命，在实际应用中，测定不可食用或变质茶中的某种特定腐败微生物，通过对茶叶中特定腐败微生物数量的预测以评估货架期是可行的，即测量一些微生物指标（比如微生物菌落总数、延迟期的时间等）来直接预测茶叶货架期受到越来越多的研究者的青睐。针对于茶叶表面存在的微生物，可根据微生物生长的修正Arrhenius 模型方程和Gompertz 的方程进行对茶叶货架期的预测[43-45]。

式中：tb表示微生物生长延迟期的时间，h；T 表示热力学温度，K；Tref表示基准温度取 273 K；μm1（h-1）和λref（h）分别表示Tref时茶叶微生物的生长速率h-1和微生物延迟期时间，h；Ea(ref)和 Ea(m)为活化能，kJ/mol；R 空气中气体常数[一般取8.314 4 J/（mol·K）]。

在 2 ℃～15 ℃条件下，E Dermesonluoglu[46]等在对蒲公英和方便色拉货架期研究时，确定以假单胞菌数为特定腐败微生物预测蒲公英粉和方便食品色拉的货架期，模型表示：

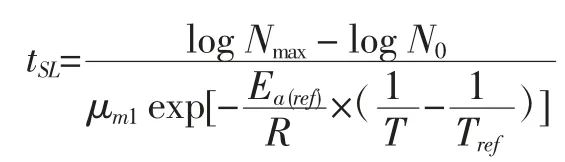
式中：tSL表示货架期，d；μm1（h-1）表示假单胞菌生长速率，h-1；Ea(ref)为活化能，kJ/mol；Nmax蒲公英粉中假单胞菌生长的最大数，CFU/g；N0蒲公英粉中假单胞菌生长的初始量，CFU/g；R 空气中气体常数 [一般取8.314 4 J/（mol·K）]。

由此可以看出，在食品贮藏过程中微生物的生长速率μm和特定腐败微生物延迟期的时间（tb）是衡量货架期的主要指标。在茶或茶产品中，如果确定了茶中特定腐败微生物达到稳定期后的最大菌落数（Nmax）和茶叶被感官拒绝时微生物的最小腐败数（Ns），则可由上式可以算出微生物的生长速率（μm）和微生物延迟期的时间（tb）。再根据Gompertz 方程模型可以计算出茶叶中特定腐败微生物数量从（N0）增值到（Ns）时的预测货架期时间（SL）[47]，其SL 的预测模型方程式为：

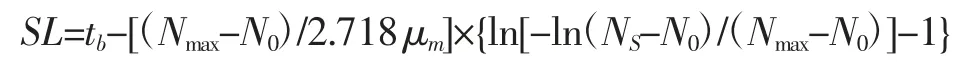
由SL 货架期模型可以看出，茶叶本身水分活度、环境的pH 值、微生物数量以及环境温度对茶叶货架期有一定的影响。茶叶货架期的寿命主要由微生物代谢和生长情况所导致，而环境因素对微生物也有一定的抑制作用。根据茶叶货架期预测模型，对于任意某茶叶在贮藏过程中，可以通过控制变量拟合出最佳的模型，为有效的延长茶叶的货架期提供了有力的科学理论基础。

4.2 量纲模型货架预测模型

很多物理因素不仅影响茶叶中微生物的生长，而且对茶叶本身品质也有有影响，特别是茶叶在贮藏过程中温度k、时间t、被微生物污染的面积s、质量m、体积v、茶叶的密度p 等因素的影响。通过量纲模型测定贮藏温度、时间、表面积、质量、体积以及密度参数，可根据建立一个函数关系式，拟合出物理变量与贮藏时间的关系，在实际预测中，可根据对这些指标的测定，即可以推断茶的贮藏时间，根据茶叶腐败变质的程度可以评估其保质期。

5 货架期预测模型存在的问题及展望

微生物种类及茶叶加工的多样性给预测微生物学及茶叶货架期的预测应用带来不小的挑战。在绝大多数微生物预测模型中，并未考虑到微生物间的竞争、促进和抑制作用[48]。近年来，茶叶货架期寿命的预测一直是茶叶行业关注的焦点[49]。为此，充分了解微生物生长及环境因素对茶叶质量和茶叶安全能作出科学合理判断是非常必要的，这提高了人们对茶叶货架期预测的可信度。影响茶叶的货架期因素有很多[50]，主要体现在茶叶微生物的影响以及茶叶本身在不同环境下贮藏的一些品质变化。基于对有害微生物生长模型的研究来预测茶叶货架期寿命越来越受到研究者们的认可，而且一般采用的是微生物生长的一级、二级模型来预测。茶叶在贮藏期间，由于所处的环境变化（理化因素、pH 值变化等）差异较大，因此对茶叶本身品质影响也比较大，也很有可能导致营养的流失，从而也会对茶叶表面的微生物也会产生一定的影响，特别是腐败菌类，当茶叶营养流失后，有利于大多数腐败菌的繁殖，相反，当茶叶在某些特定条件下保藏，也可能会有利于另一些茶叶微生物的生长，例如大肠菌群、霉菌和酵母；当微生物量达到一定的数量是，很大程度上会对茶叶本身质量品质带来极大的影响，由此可知，影响茶叶品质的因素可能会对茶叶微生物的生长产生一定影响，而微生物的生长繁殖对茶叶品质也会带来影响，这两种情况作用，从而降低了茶叶货架期的寿命。

随着微生物分析、数学统计以及感官分析等技术的发展，在综合考虑各指标对茶叶影响时，还可以根据基于现代技术来进行对茶叶货架期的评价分析，比如用电子鼻气味指纹图谱技术可以准确探测茶叶感官变化，特别是对茶叶挥发性气味的直接反应来预测货架期。除本研究表述外的其他因素也应该全面考虑，比如包装茶叶的材料，包装材料的密封性以及材料的几何学（表面积、形状大小、规格等）多方面因素综合考虑。通常茶叶货架期茶叶品质的变化，由理化、微生物和感官等多因素综合表现，在理论分析的基础上，还需要借助数学统计方法，将多种因素变量进行回归拟合，实现多变量拟合预测模型。茶叶货架期较长，对模型进行可靠性分析很有必要，结合所建的货架预测模型和现代一些检测技术不仅促进了对茶叶货架期预测的发展，而且使得茶叶货架期品质评价体系得以实施和发展，为茶叶领域提供了合理的科学研究方法。微生物预测模型是预测微生物生长的科学依据，而预测精度取决于对所建立的数学模型准确性，但在模型建立时，往往会使得复杂化，从而不便于合理的预测，再加上茶叶组分复杂，不同微生物的生长特性有所差异，许多相辅因素变量尚未列入预报的系统，预测结果并不理想，预测模型在具体运用上和实际研究中还有待改进，导致对茶叶货架期的预测会出现一些缺陷。因此，更好的通过微生物生长模型来预测茶叶货架期，还有很多相关领域值有待我们去探讨发现、研究和解决。