基于线性拟合和差值补偿的跳线计算方法研究

李铁鼎，雷雨泽，程述一2，刘文勋，周古月

(1. 中国电力工程顾问集团中南电力设计院有限公司，湖北 武汉 430071; 2. 国网经济技术研究院有限公司，北京 102209)

0 引 言

耐张塔跳线系统是高压输电线路的重要组成部分，由硬跳线和软跳线构成。跳线安装必须满足带电部分与杆塔构件的最小间隙、压接工艺及成形美观等要求[1]。

由于跳线系统较复杂，跳线设计包含跳线长度L软、跳线弧垂、平视弧垂计算等，其主要设计边界条件又包含转角度数、耐张串长度、耐张串倾斜角、杆塔尺寸、硬跳线长度等。现有研究成果均需进行逐塔、逐相计算[2-3]，设计方法、计算过程复杂且施工过程的操作性较差。下面提出一种基于线性拟合和差值补偿法的1000 kV特高压交流输电线路跳线安装设计方法，有利于提高跳线设计、安装工作效率和工作质量；减少因杆塔尺寸、串长、串重、转角度数等边界条件变化时带来的重复计算跳线线长工作。

1 理论依据

1.1 最小二乘法原理

已知两变量为线性关系y=kx+b，实验获得其n组含有误差的数据(xi，yi)。若将这n组数据代入方程求解，则k、b之值无确定解。最小二乘法其基本思想是拟合出一条“最接近”这n个点的直线。在这条拟合的直线上，各点相应的y值与测量值对应纵坐标值之偏差的平方和最小。根据统计理论，参数k和b计算公式为

(1)

(2)

1.2 相关系数

相关系数γ表示数据(xi，yi)相互联系的密切程度以及拟合所得的线性方程的可靠程度。γ的计算公式为

(3)

式中，γ的值在-1～+1之间，γ的绝对值越接近1，表明(xi，yi)相互联系越密切，线性方程的可靠程度越高，线性越好。

1.3 跳线计算拟合模型

以2013年版《国家电网公司输变电工程通用设计1000 kV输电线路分册》[4]中的单回路10A杆塔模块为计算模型，杆塔示意如图1所示。跳线装置的侧视图如图2所示。

图1 杆塔示意

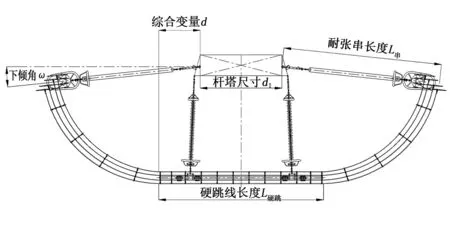
图2 跳线装置侧视

确定拟合函数相关变量：

1)确定杆塔尺寸

根据耐张塔结构详图确定耐张串挂点位置及大、小号侧挂点间距离d1。

2)确定耐张串长度

根据不同污区、冰区的绝缘配置，确定耐张串实际长度L串。

3)确定杆塔尺寸综合变量

由杆塔尺寸d1、硬跳线长度L硬跳，确定耐张串挂点与硬跳端部沿线路方向的距离d=(L硬跳-d1)/2。

4)确定倾斜角

根据实际定位成果计算耐张串下倾角ω。

5)确定跳线基准长度

根据转角度数θ查本标准设计典型边界下的跳线基准长度L0。

6)计算修正后的实际跳线长度

根据实际耐张塔边界条件和典型边界条件的对比，通过差值补偿公式L(ω，L串，d，L0)=A(ω-ω0) +B(L串-L串0)-C(d-d0) +L0计算出耐张塔实际边界条件下的跳线线长。

2 跳线安装设计要求

1)跳线型式

1000 kV特高压交流线路耐张塔跳线由硬跳线部分和软跳线部分组成。硬跳线是由管、棒、角钢、槽钢和金具组成，一般分为铝管式跳线和笼式跳线，目前特高压交流线路一般采用悬挂的笼式跳线；软跳线是由多分裂软导线和金具组成[5]。

1000 kV特高压交流线路耐张塔跳线一般采用八分裂形式，呈正八边形排列，分裂间距为400 mm。

2)跳线绝缘子串的布置

笼式跳线含两个跳线绝缘子串，两跳线串的间距为8～10 m(根据横担宽度和硬跳线长度确定)，跳线串高压侧与骨架钢管连接，低压侧与横担连接，跳线串布置方式如图2所示。

3)跳线间隔棒布置

耐张塔每段软跳线部分安装3～4个跳线间隔棒，其中1个间隔棒安装在距离耐张线夹引流板1.0 m的位置，另1个间隔棒安装在笼式硬跳线出口1.5 m的位置，其余间隔棒按剩余软跳线长度等距离安装。

4)跳线安装

跳线宜使用未受过张力的导线制作，跳线安装人员不能蹬踩跳线，以保证跳线成形美观。在安装耐张绝缘子串时，必须注意引流板的方向，将其方向调整好后再进行压接。

5)跳线间隙校核

跳线安装时应注意，由于绝缘子及金具等尺寸存在误差，且影响跳线长度的其他因素也较多，实际工程使用应在参考“跳线安装标准设计”的同时，必须保证各种工况下跳线对塔身的电气间隙满足要求。1000 kV单回路线路电气间隙控制值如表1所示。

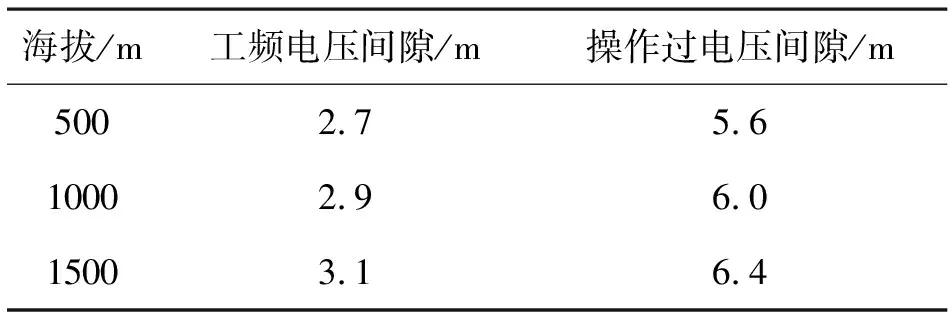
表1 电气间隙控制值

注：跳线对塔身最小间隙值应不小于表1所述控制值的1.1倍。

3 跳线设计计算实例

3.1 单回路耐张塔边相跳线安装设计边界条件

边相跳线标准设计的边界条件详见表2。

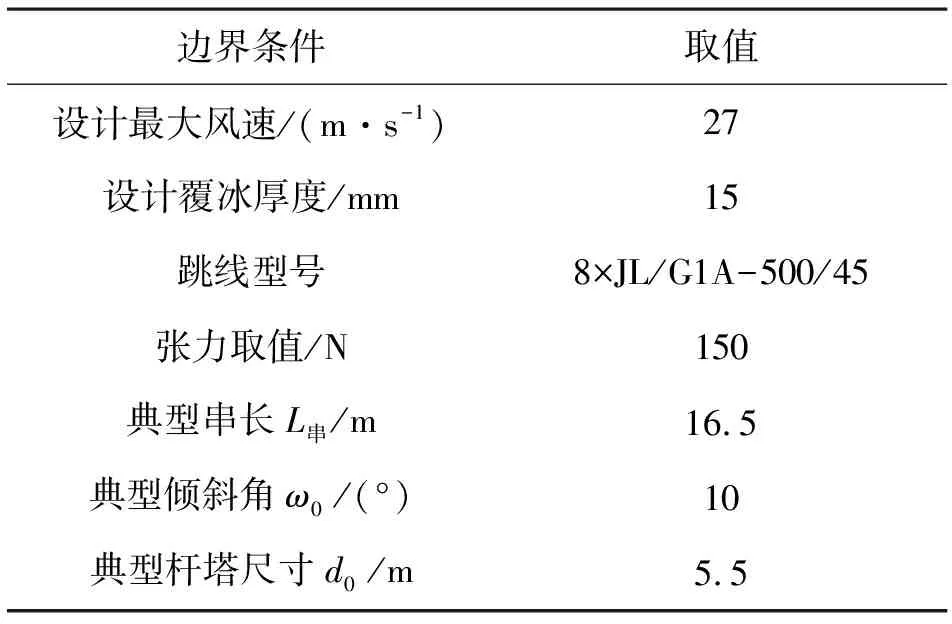
表2 边界条件

3.2 单回路耐张塔边相跳线安装设计

3.2.1 典型边界条件下的跳线安装表

一型转角塔使用转角度数为0°～10°塔，计算典型边界条件下(ω0=10°，L串0=16.5 m，d0=5.5 m)的跳线线长标准值L0如表3所示。由于跳线串倾斜度数较小，跳线串对硬跳线的垂直方向位置影响很小，无需考虑跳线串倾斜情况对跳线线长的影响。

3.2.2 耐张串倾斜角对跳线安装和线长影响

改变耐张塔倾斜角，并保持其他典型边界条件中不变，计算倾斜角ω变化对跳线线长的影响，如图3所示。

表3 典型边界条件下的边相跳线线长

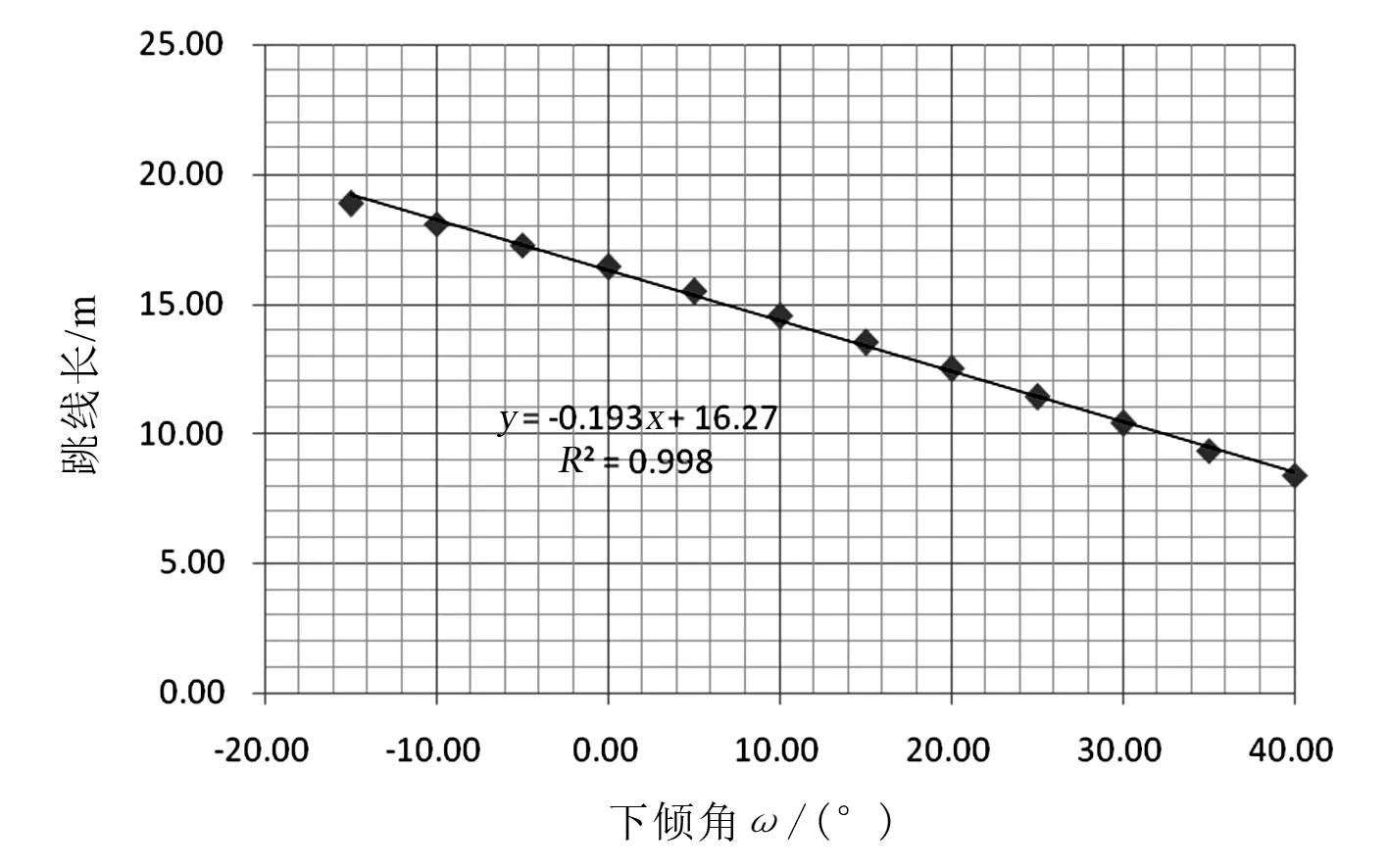
(a)内角侧

(b)外角侧图3 边相跳线线长与倾斜角关系

以倾斜角ω为变量，利用最小二乘法进行线性拟合，拟合结果如下：

内角侧，L(ω)=- 0.193ω+16.27

外角侧，L(ω)=- 0.19ω+16.8

(4)

3.2.3 耐张绝缘子串长对跳线安装和线长影响

改变耐张串的长度，保持其他典型边界条件不变，计算耐张串串长变化对跳线线长的影响，如图4所示。

以耐张串串长L串为变量，利用最小二乘法进行线性拟合，拟合结果如下：

内角侧，L(L串)= 1.047L串-2.589

外角侧，L(L串)= 1.079L串-2.527

(5)

(a)内角侧

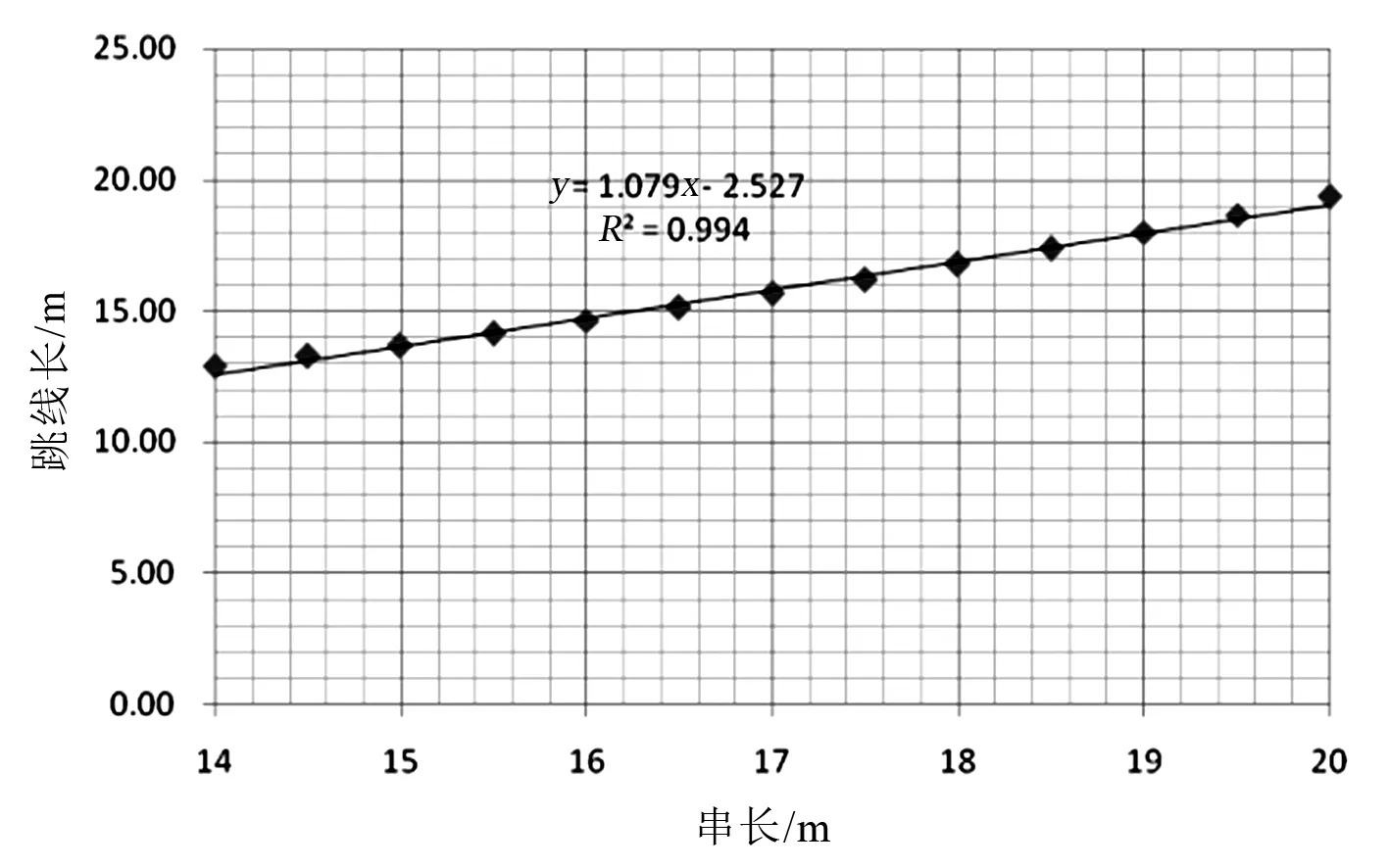
(b)外角侧图4 边相跳线线长与串长关系

3.2.4 杆塔尺寸综合变量d变化对跳线安装和线长影响

改变杆塔尺寸综合变量d，保持其他典型边界条件不变，计算杆塔尺寸综合变量d对跳线线长的影响，如图5所示。

以杆塔尺寸综合变量d为变量，利用最小二乘法进行线性拟合，拟合结果如下：

内角侧，L(d)= -1.081d+20.46

外角侧，L(d)= -1.067d+20.97

(6)

3.2.5 跳线线长计算

根据跳线线长计算结果和拟合结果，跳线线长与单一变量(ω、L串或d)呈线性关系，于是，为避免复杂的线长计算过程，改变传统跳线计算方式，可以以典型边界条件下线长为基础，通过各变量差值补偿进行跳线设计：

1)通过《电力工程高压送电线路设计手册》中线长计算公式，计算得典型边界条件下的跳线线长L0。

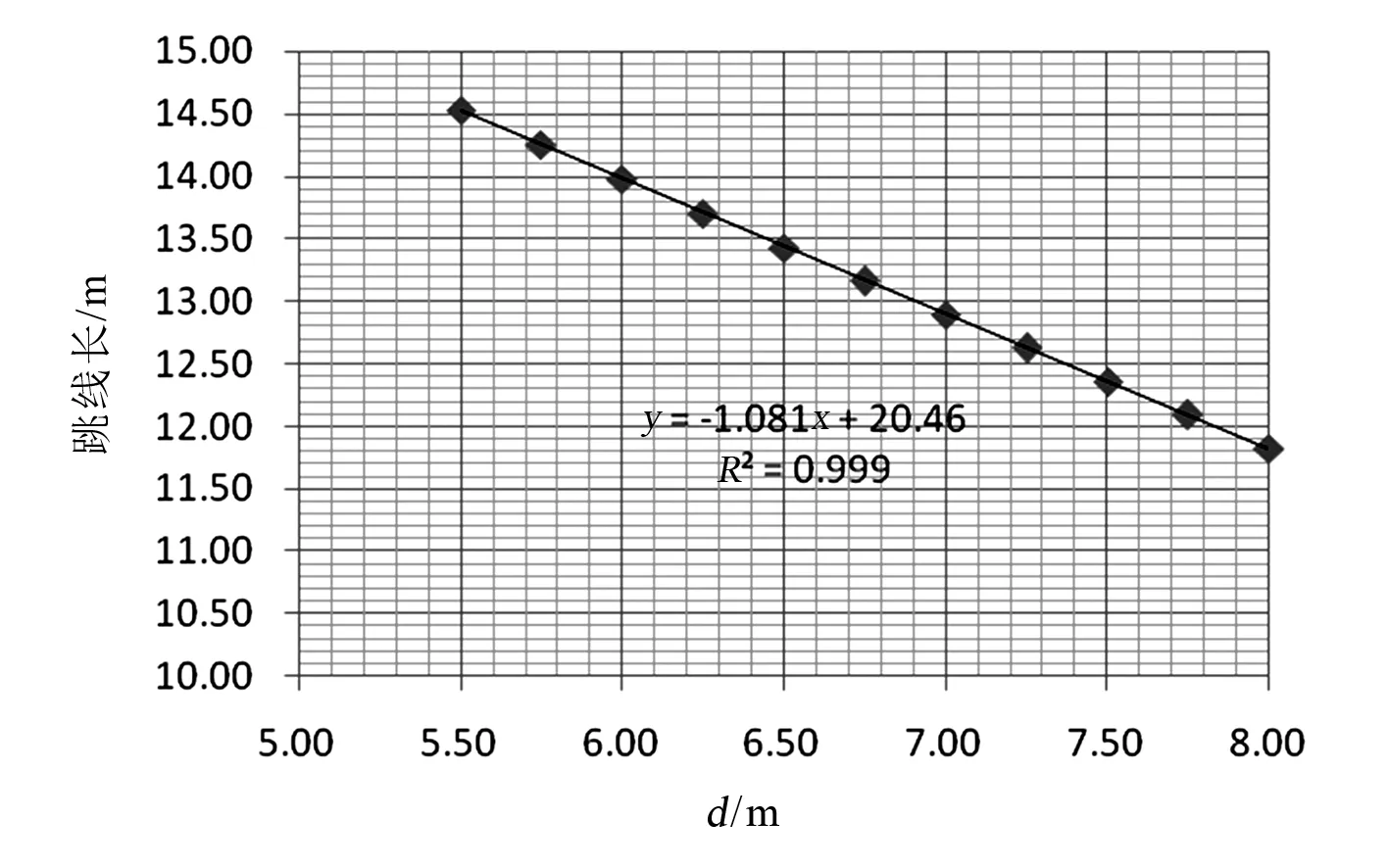
(a)内角侧

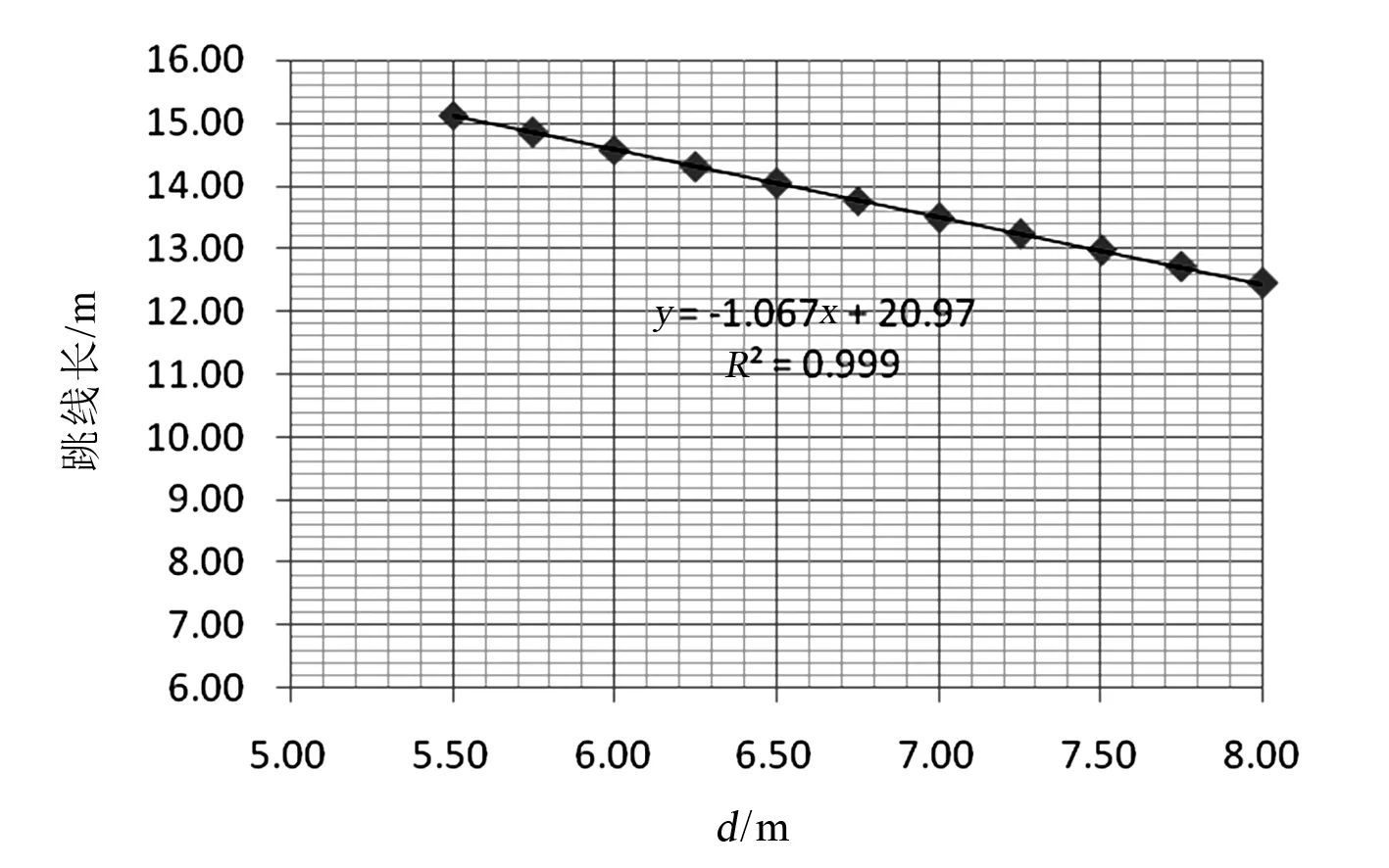
(b)外角侧图5 边相跳线线长与杆塔尺寸综合变量d关系

2)通过线性函数拟合结果计算不同边界条件(ω、L串或d)变化时的跳线长度补偿值△L串、△Lω和△Ld。

3)通过差值补偿法确定不同边界条件的跳线线长，由L=L0+△L串+△Lω+△Ld计算出实际所使用耐张塔的跳线长度，根据第3.2.2至3.2.4节中各单一边界条件与跳线线长的线性拟合结果得出跳线线长计算公式：

内角侧：L(ω，L，d，L0)=-0.193(ω-ω0)+

1.047(L-L串0)- 1.081(d-d0)+L0

外角侧：L(ω，L，d，L0)=-0.19(ω-ω0)+

1.079(L-L串0)- 1.067(d-d0)+L0

(7)

式中：ω0、L串0和d0分别表示典型边界条件倾斜角、串长和杆塔尺寸综合变量d的取值；L0表示典型边界条件下的跳线长度；ω、L串和d分别表示设计倾斜角、串长和杆塔尺寸综合变量；△L串、△Lω和△Ld分别表示串长、横担宽度和倾斜角分别变化时，跳线线长与典型边界条件下长度L0的差值。

3.3 单回路耐张塔中相跳线安装设计边界条件

根据单回路10A模块参数确定该标准设计的边界条件见表4。

表4 中相跳线边界条件

3.4 单回路耐张塔中相跳线安装设计

耐张塔中相绕跳跳线如图6所示。

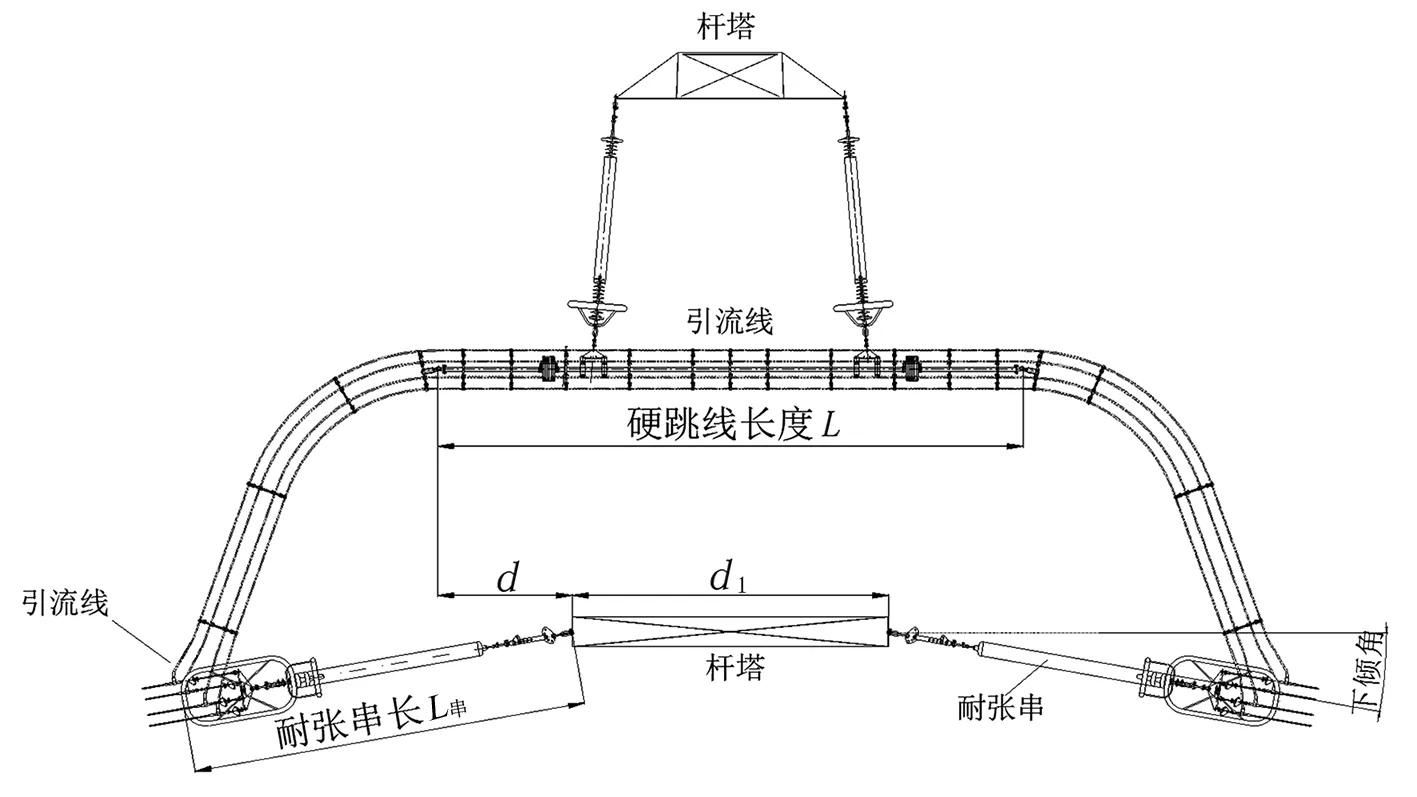
图6 耐张塔中相绕跳跳线

与耐张塔边相一样，耐张串长度L串、倾斜角度数ω、转角度数θ和杆塔尺寸综合变量d对跳线的影响较大。拟合结果表明：与边相直跳不同，单回路耐张塔中相绕跳跳线线长与串长L串、杆塔尺寸变化参数d及转角度数θ基本呈线性关系。因此，设计以典型边界条件(耐张串长度L串0、转角度数θ0和杆塔尺寸变化参数d0)为基础，通过单变量线性差值的方法确定不同耐张串倾斜角的跳线线长。

3.4.1 典型边界条件下的跳线线长

确定典型边界条件下(ω0=10°，L串0=16.5 m，d0=5.5 m)的跳线线长标准值L0如表5所示。

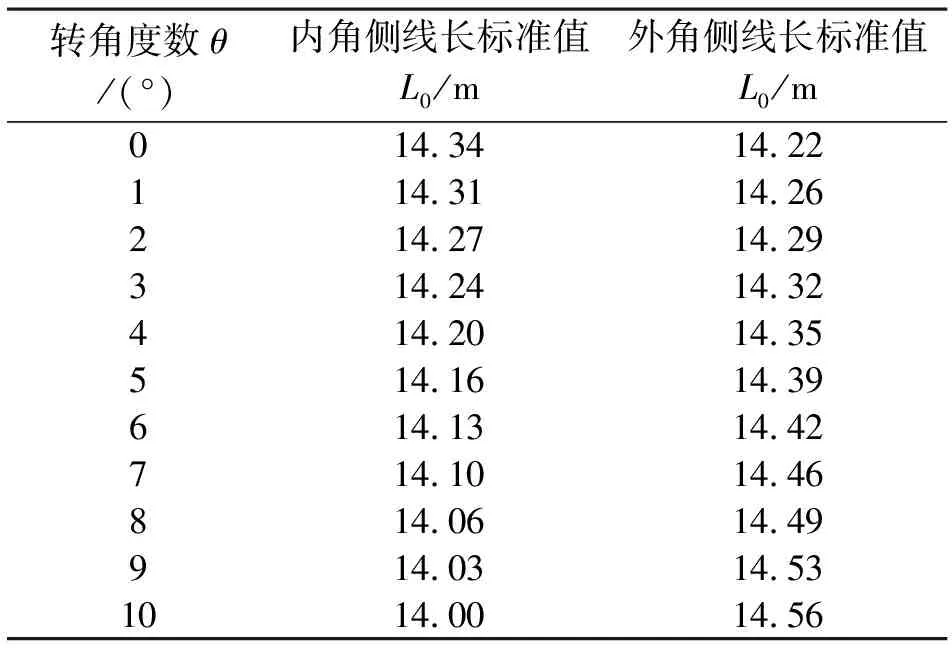
表5 典型边界条件下的中相跳线线长

3.4.2 耐张串下倾角对跳线安装和线长影响

只改变转角度数θ，其他典型边界条件不变，计算分析转角度数θ变化对跳线线长的影响。跳线线长随转角度数θ变化的曲线如图7所示。

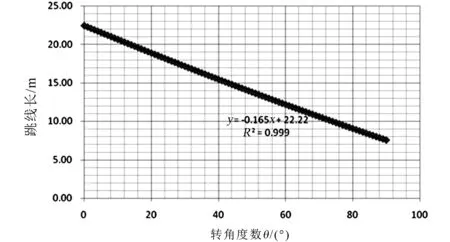
图7 中相跳线线长与转角度数的关系

以转角度数θ为变量，利用最小二乘法进行线性拟合，拟合结果如下：

L(θ)=- 0.165θ+22.22

(8)

3.4.3 耐张绝缘子串长对跳线安装和线长影响

跳线线长与随耐张串串长变化的曲线如图8所示。

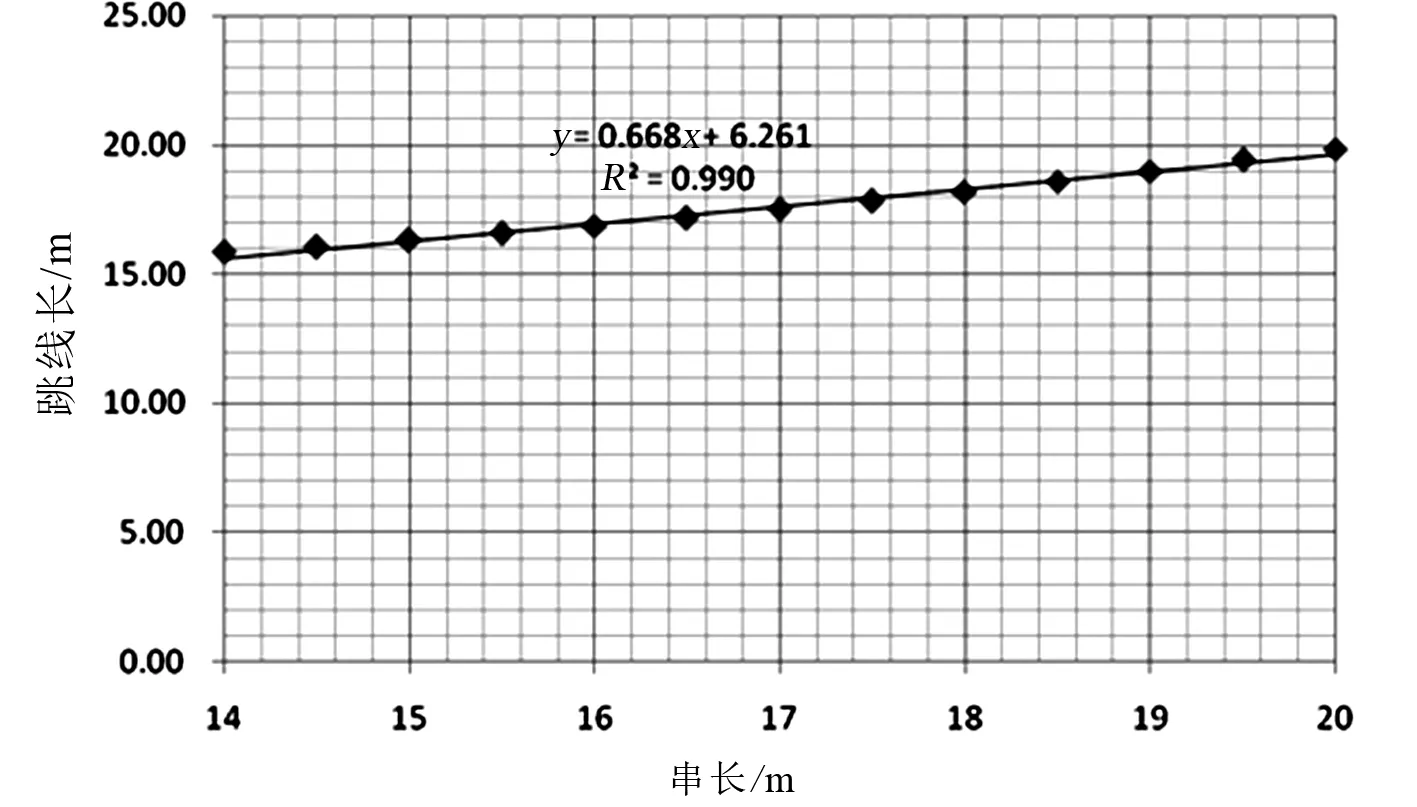
图8 中相跳线线长与串长的关系

以耐张串串长L串为变量，利用最小二乘法进行线性拟合，拟合结果为

L(L串)= 0.668L串+6.621

(9)

3.4.4 杆塔尺寸综合变量d变化对跳线安装和线长影响

跳线线长与杆塔尺寸综合变量d变化的曲线如图9所示。

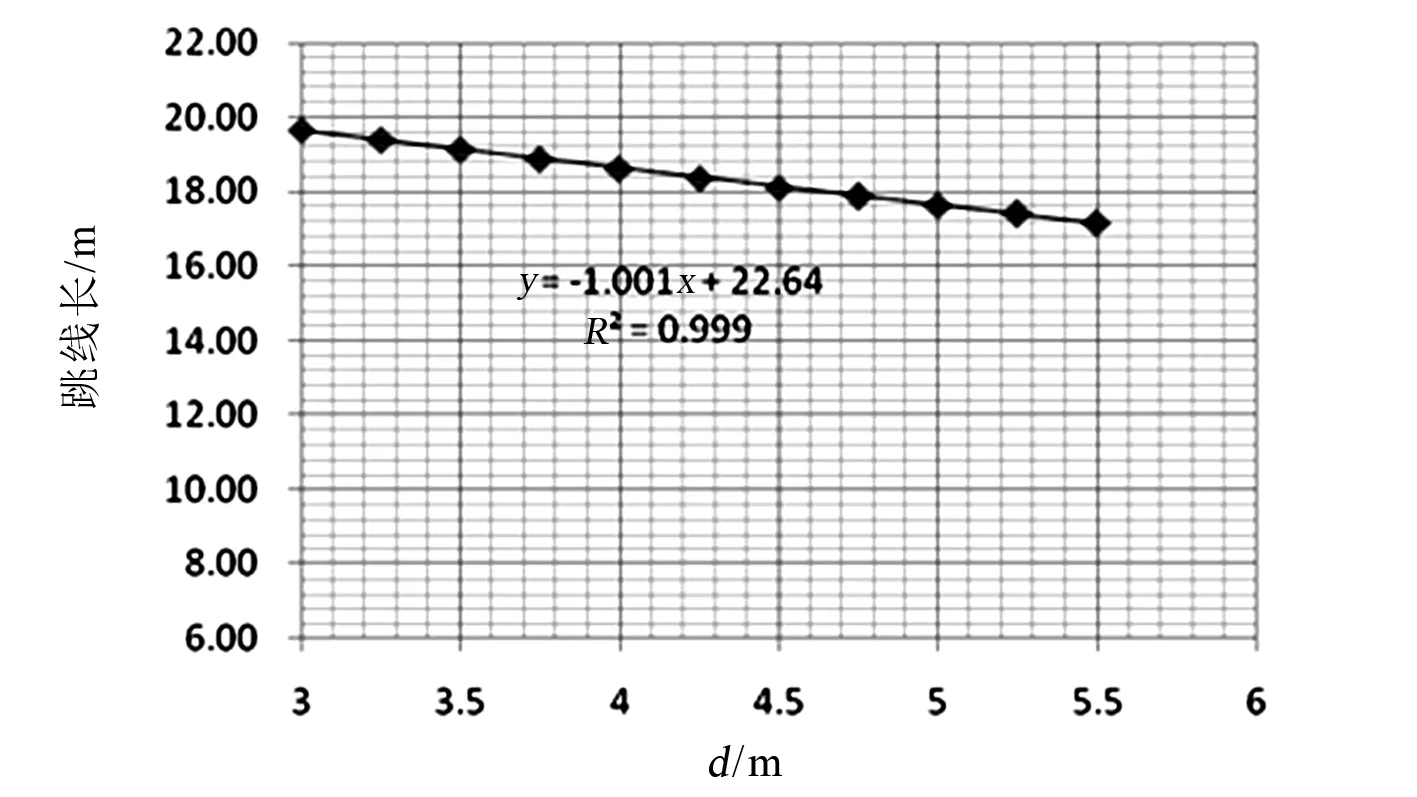
图9 中相跳线线长与杆塔尺寸综合变量d关系

以杆塔尺寸综合变量d为变量，利用最小二乘法进行线性拟合，拟合结果如下：

L(d)= -1.009d+22.67

(10)

3.4.5 跳线线长计算

根据跳线线长计算结果和最小二乘法拟合结果，跳线线长与单一变量(θ、L串或d)呈线性关系。为避免复杂的线长计算过程，改变传统跳线计算方式，以典型边界条件下线长为基础，通过各变量差值补偿进行跳线设计。

首先，通过《电力工程高压送电线路设计手册》中线长计算公式，计算得典型边界条件下的跳线线长L0；然后通过函数拟合结果计算不同边界条件(θ、L串或d)变化时的跳线长度补偿值△L串、△Lω、△Ld；最后，通过差值补偿法确定不同边界条件的跳线线长。由L=L0+△L串+△Lω+△Ld计算跳线长度。

根据第3.4.2至3.4.4节中各单一边界条件与跳线线长的线性拟合结果得出中相跳线线长计算公式：

L(θ，L，d，L0)=-0.165(ω-ω0)+0.668(L-

L串0)- 1.001(d-d0)+L0

(11)

3.5 误差分析

根据第3.2.5节及第3.4.5节线性拟合结果采用差值补偿法计算不同边界条件 (转角度数θ为0～90°、绝缘子串长L串为15～19 m、杆塔尺寸综合变量d为4.5～6.5 m、下倾角ω为-10°～40°随机组合)的跳线线长，计算结果与《电力工程高压送电线路设计手册》中普通线长计算公式计算结果[6]进行对比分析，如表6、表7所示。

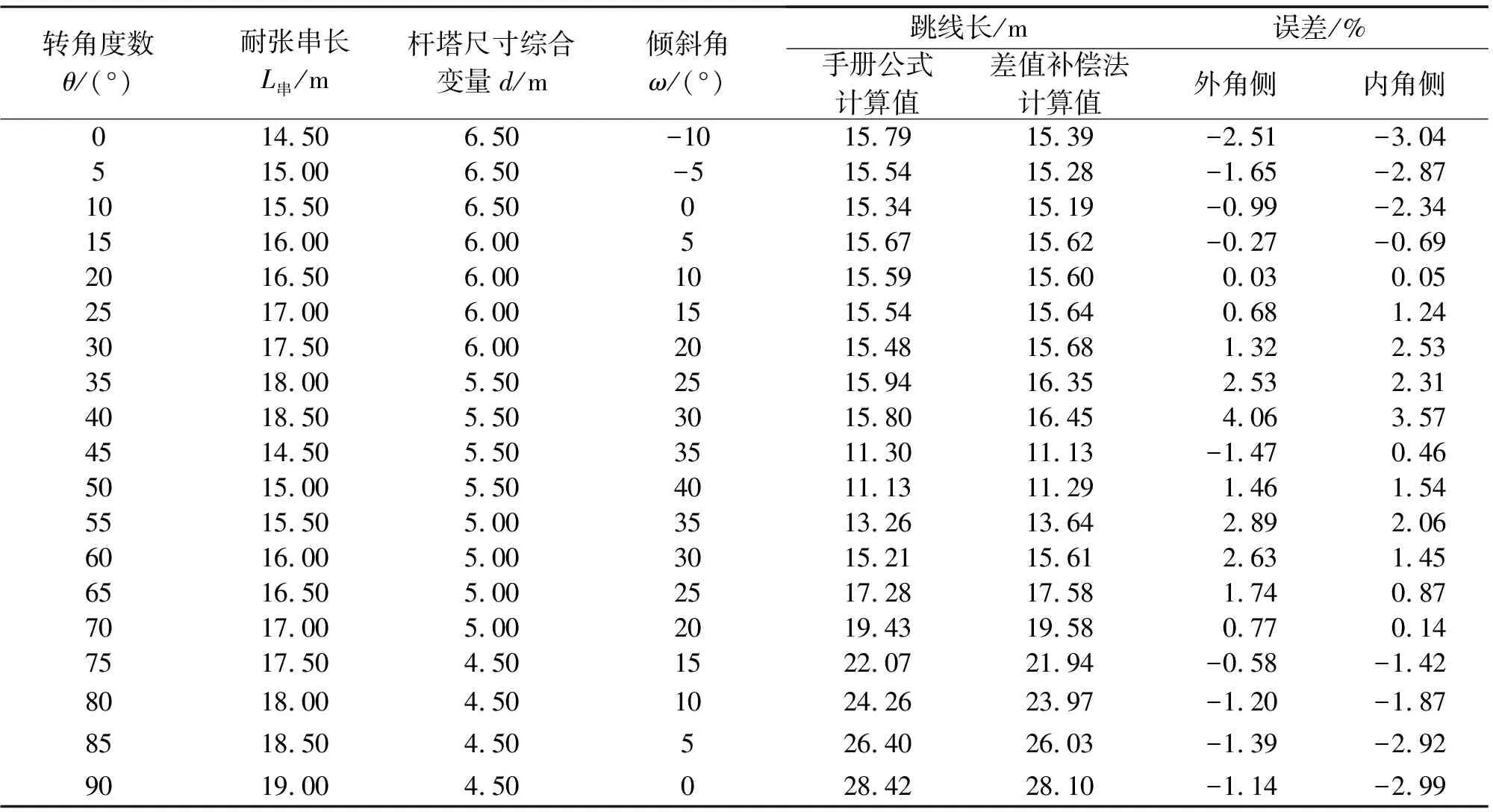
表6 边相跳线安装设计(差值补偿法)计算误差分析

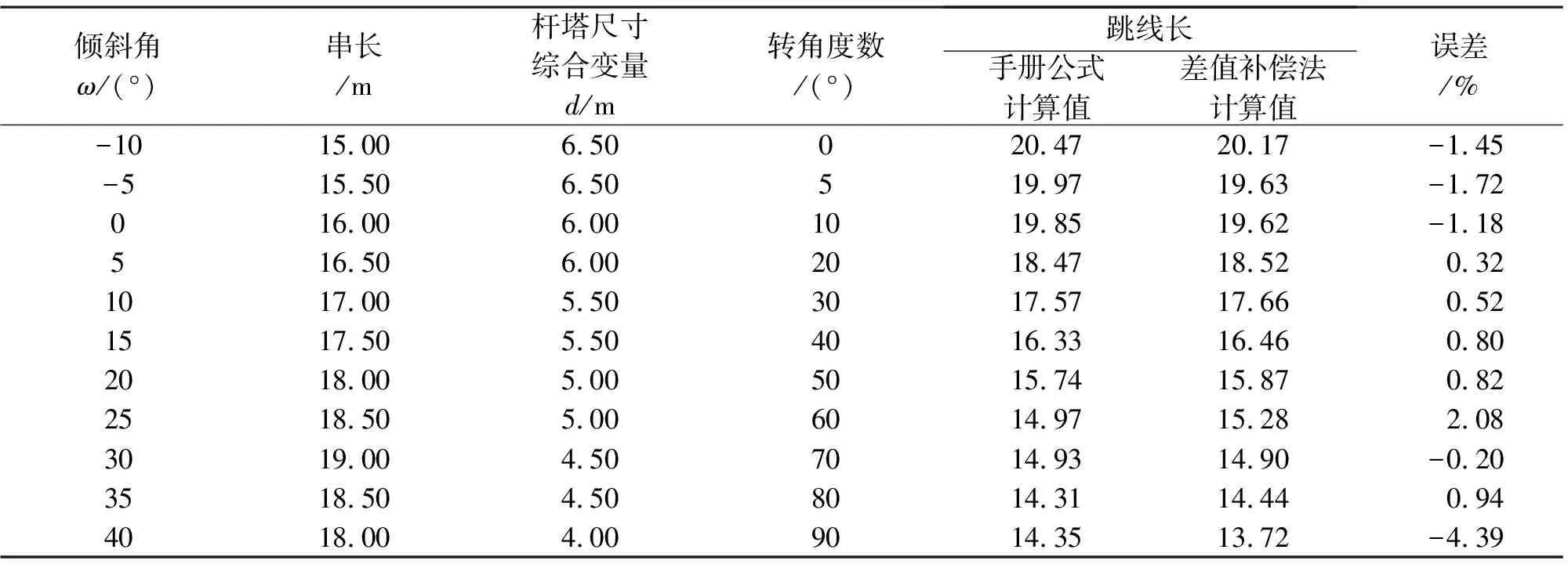
表7 中相跳线安装设计(差值补偿法)计算误差分析

以上数据表明:采用差值补偿法的计算结果与采用《电力工程高压送电线路设计手册》[6]线长计算公式的计算结果吻合较好，计算结果的最大偏差不超过4.5%。

4 结 语

经过实践验证，依照基于线性拟合和差值补偿法的1000 kV特高压交流输电线路跳线安装设计方法进行单回路跳线设计，有效地简化了设计流程，减少了40%设计时间，对减少重复计算时间也具有实际意义。